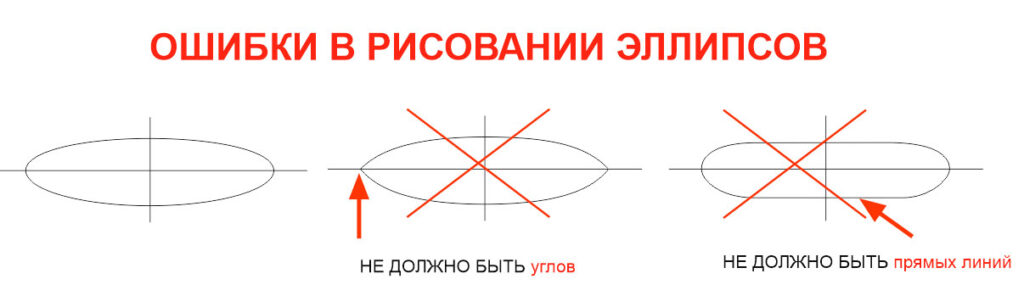
- Перспектива окружности в горизонтальной плоскости.
- Упражнение 1.
- Упражнение 2.
- Перспектива окружности в вертикальной или наклонной плоскости.
- Перспективные зарисовки с натуры.
- Рисунок с натуры коробки или книжки.
- Упражнение 4
- Упражнение 5
- РИСУНОК С НАТУРЫ КРУЖКИ.
- Упражнение 6
- Упражнение 7.
- Проецирование окружности
- Как начертить наклонную окружность
- 📸 Видео
Видео:2 2 3 построение изометрии окружностиСкачать

Перспектива окружности в горизонтальной плоскости.
Множество предметов, находящихся вокруг нас, имеют формы,
очертанием которых является окружность.
Чаще всего эта окружность находится в горизонтальной плоскости: это могут быть края чашки, стоящей на столе или табуретка с круглым сидением.
Если такая окружность находится на уровне наших глаз, на линии горизонта, мы видим ее как прямую линию.
Если мы смотрим на окружность сверху, то мы видим ее без искажений, как окружность.
Во всех остальных случаях, когда окружность располагается в горизонтальной плоскости, мы видим ее как эллипс.*
То есть, как лекальную кривую, симметричную относительно двух взаимно перпендикулярных осей.
При чем, одна из этих осей ВСЕГДА строго вертикальна, а другая, соответственно, горизонтальна.
*Строго говоря, изображение окружности в перспективе не является эллипсом, так как дальняя от нас его часть чуть меньше, чем ближняя. И, соответственно, он не симметричен относительно горизонтальной оси.
Соотношение между длинами осей эллипса называют раскрытием.
Грубо говоря, чем больше эллипс похож на круг, тем более он раскрытый.
В изображении эллипсов в горизонтальной плоскости есть два основных правила:
- Чем дальше находится эллипс от линии горизонта, тем более раскрытым мы его картинка
- Дальняя часть эллипса ЧУТЬ меньше, чем ближняя.
Легко понять, почему это так , построив в перспективе окружность вписанную в квадрат.

Видео:окружность в изометрии ХYСкачать
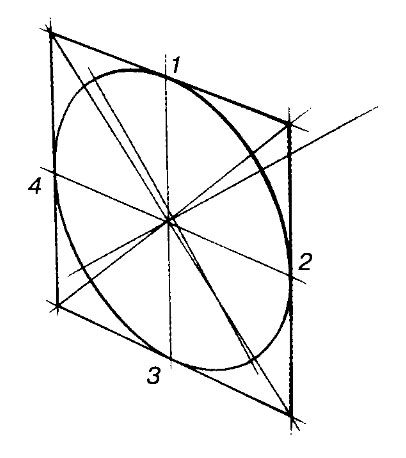
Упражнение 1.
Постройте окружность тем же способом, с той же точкой схода, но выше линии горизонта. Выделите более толстой линией ее передний край.
ОБРАТИТЕ ВНИМАНИЕ что в рисунке окружности, лежащие в горизонтальной плоскости мы НЕ строим с помощью описанного квадрата. Так как этот даёт искажения, если точка схода для квадрата не лежит на вертикальной оси эллипса.
Мы проводим две оси эллипса и задаем степень раскрытости на глаз, но учитываем положение эллипса относительно линии горизонта и других эллипсов.
Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Упражнение 2.
На рисунках изображена последовательность построения цилиндра и конуса.

Нарисуйте цилиндры и конусы выше и ниже линии горизонта . Раскрытие эллипсов задаём на глаз. Окружность в квадрат не вписываем.
Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Перспектива окружности в вертикальной или наклонной плоскости.
С окружностями в вертикальной плоскости нам приходится иметь дело достаточно часто. Например, рисуя арки в архитектуре.
Самый простой случай — когда окружность находится в плоскости параллельной картинной. Тогда мы видим ее без искажений.

Bernardo Bellotto1743/1744
Если окружность находится под углом к картине, для построений мы также используем описанный квадрат. Этот способ применяется как в черчение, так и в рисунке, так как на глаз нарисовать окружность в таком ракурсе очень сложно .
В этом курсе мы только знакомимся со способом построения окружности в вертикальной плоскости. Но если у вас есть желание, подробно об этом можно прочитать в учебнике Осмоловской (ст. 26) или, в упрощенном виде у Шарова и Барщ.
Видео:Построение окружности в изометрии.Скачать

Перспективные зарисовки с натуры.
Мы закончили блок теории построений. Теперь начинаем работать с натуры.
На этом этапе важно осознать, что рисунок — не черчение. В рисунке мы не пользуемся линейкой, редко строим точки схода на дополнительном листе. Наша задача, зная, какие построения применялись бы для перспективного чертежа, сделать минимум из них на глаз так, чтобы в результате получилось убедительное изображение, соответствующее основным правилам перспективы.
Рисование с фотографии.
Я вас очень прошу, по крайней мере на начальном этапе не срисовывать с фотографии, даже называя это рисованием с референсов.
Рисуя с фото вы НЕ развиваете пространственное воображение и умение на плоскости изображать объем. Вы только учитесь копировать с одного листа на другой пятна тона. Это, конечно, тоже полезный навык но для хорошего рисунка его не достаточно.
Постановка натуры.
Правильная постановка натуры помогает избежать многих ошибок в рисунке и делает работу легче и приятнее.
Поэтому я очень прошу вас уделить этому внимание.
- Организуйте рабочее место так, чтобы смотреть на натуру все время с одной точки зрения. Если вы работаете в несколько сеансов, запомните, где вы стояли или сидели относительно натуры. Чтобы не оказалось так, что половина предметов на работе у вас сделана с одной точки зрения, а половина — с другой.
- Не садитесь слишком близко или слишком далеко от натуры. Между вами и натурой должно укладываться примерно два ее размера.
- В начале обучения, старайтесь ставить предметы на контрастный фон, чтобы их очертания хорошо читались.
- В начале обучения, не ставьте предметы против света или с несколькими источниками света. Старайтесь чтобы освещение было сбоку и форма предметов хорошо читалась.
- Отходите от рисунка или переворачивание его кверх ногами. Так вы увидите ошибки. Ещё можно смотреть на работу в зеркало.
Видео:Как начертить овал во фронтальной плоскостиСкачать

Рисунок с натуры коробки или книжки.
- Задаем положение переднего вертикального ребра и определяем, под каким углом к горизонтали мы видим нижние ребра.
- Определяем пропорции.Смысл рисования с натуры в том, чтобы она была передана точно. Эту задачу не решить без соблюдения пропорций. То есть отношений разных размеров объектов друг к другу. Если вы сделаете лицо портретируемого в два раза шире, чем на самом деле, вряд ли он вас за это поблагодарит. Для измерения пропорций есть достаточно простые приемы. О них я рассказываю на этом видео.
Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Упражнение 4
Нарисуйте с натуры предмет с прямыми ребрами ( книжку, коробку и т. п.)
Мы НЕ рисуем с фото, мы НЕ копируем рисунок, разобранный выше.
Видео:Часть 1. Изометрическая проекция. (стр. 29)Скачать

Упражнение 5
Нарисуйте два предмета с прямыми ребрами, один из которых стоит на другом.
Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

РИСУНОК С НАТУРЫ КРУЖКИ.
Для постановки нужно выбрать кружку простой цилиндрической формы, с ручкой. Саму кружку мы видим без сокращений, поэтому отношение высоты и ширины можно измерить, приложив карандаш непосредственно к натуре.
- Начинаем с построения цилиндра. Помним, что чем дальше эллипс от линии горизонта, тем более он раскрыт.
- Строим толщину стенок кружки.
- Строим ручку: начинаем с мест крепления ручки, обратите внимание, что они находятся на одной вертикальной оси.
- Строим ось ручки. обратите внимание, что она лежит в плоскости, проходящей через центр цилиндра.
- Строим внешнюю, внутреннюю и боковую поверхности ручки.
Видео:Построение окружности в диметрииСкачать

Упражнение 6
Нарисуйте кружку с натуры.
Видео:Построение прямоугольной изометрии окружностиСкачать

Упражнение 7.
Нарисуйте ту же кружку в другом ракурсе по представлению(не глядя на натуру)
Видео:Школа для родителей. Циркуль, окружность, радиус, диаметр.Скачать

Проецирование окружности
Окружность с центром О, рассматриваемая как плоская фигура, проецируется без искажения на ту плоскость, которой она параллельна (рис. 6.5). При этом две другие ее проекции есть отрезки, параллельные осям проекций и равные по длине диаметру окружности.
Если окружность наклонена к плоскости проекций, то ее проекция представляет собой эллипс, большая ось которого равна диаметру окружности. Величина малой оси зависит от угла наклона плоскости окружности к плоскости проекций.
Окружность, изображенная на рис. 6.6, перпендикулярна плоскости проекций П и наклонена к плоскости проекций к2, поэтому ее фронтальная проекция — эллипс. Большая ось этого эллипса С «И « представляет собой проекцию диаметра окружности, который без искажения проецируется на плоскость проекций л2. Таким образом, она перпендикулярна плоскости проекций Л1 и параллельна плоскостям проекций 7^2 и Лз. Малая ось эллипса является проекцией диаметра АВ, перпендикулярного СИ. Ее величину на плоскости проекций п2 определяют с помощью линий проекционной связи, проведенных через точки А’ и В’.
Промежуточные точки эллипса находят с помощью дополнительной плоскости проекций тс4, которую располагают параллельно плоскости окружности, поэтому окружность проецируется на нее без искажения. Вначале строят новую проекцию центра окружности — точку О™ и на плоскости тс4 описывают заданную окружность. Затем на окружности намечают 8 или 12 произвольных точек и находят их проекции в системах плоскостей щ/щ и щ/л2. На рис. 6.6 приведено построение только для двух промежуточных точек 1 и 2; остальные строят аналогично.
Окружность, расположенная в плоскости общего положения, проецируется на все основные плоскости проекций в виде эллипсов, большие оси которых равны ее диаметру. Величины малых осей обычно различны и зависят от углов

наклона заданной плоскости, в которой расположена окружность, к плоскостям проекций.
Если эллипс представляет собой проекцию окружности, то на горизонтальной проекции его большая ось расположена на горизонтальной прямой плоскости, на фронтальной — на фронтальной прямой и на профильной — на профильной прямой.
Построение в плоскости общего положения а(Иа п /а) (рис. 6.7) проекций окружности с центром в точке О, расположенной на горизонтальной прямой /га, и с радиусом, равным /?, начинают с определения проекций осей эллипса.
На горизонтальной проекции окружности по прямой /га‘ вправо и влево от точки О‘ откладывают радиус окружности Л, получая при этом точки А’ я В’. Сделав замену плоскостей проекций щ/л2 —> п/щ, где п4_1_ Иа, и построив новую проекцию окружности в виде отрезка С ,У /) |У , равного диаметру окружности, строят с помощью точек С’ и /)’ малую ось эллипса на горизонтальной проекции (направления построений указаны стрелками).
Для фронтальной проекции окружности через точку О « проводят проекцию прямой, параллельной^’, и на ней вправо и влево от точки О » откладывают радиус окружности Я, получая точки Е «, Е». Сделав замену плоскостей проекций П/П2 —> П2/Л5, где п5 Е/а, и построив новую проекцию окружности в виде отрезка, равного диаметру окружности, строят на фронтальной проекции с помощью точек 1У, малую ось эллипса.
Таким образом, на каждой проекции есть по четыре точки, принадлежащие проекции окружности: точки Л ‘, ВС‘, В‘ и Е «, Е», К «, Ь». Проводя из них линии проекционной связи, получают восемь точек для построения горизонтальной и фронтальной проекций эллипса.
Видео:Построение пятиугольника циркулемСкачать

Как начертить наклонную окружность
Контрольные задания по теме: эпюр № 6
Для наглядного изображения предметов (изделий или их составных частей) рекомендуется применять аксонометрические проекции, выбирая в каждом отдельном случае наиболее подходящую из них.
Сущность метода аксонометрического проецирования заключается в том, что заданный предмет вместе с координатной системой, к которой он отнесен в пространстве, параллельным пучком лучей проецируется на некоторую плоскость. Направление проецирования на аксонометрическую плоскость не совпадает ни с одной из координатных осей и не параллельно ни одной из координатных плоскостей.
Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям. Под коэффициентом искажения понимается отношение величины изображения в аксонометрической проекции к величине изображения в ортогональной проекции.
В зависимости от соотношения коэффициентов искажения аксонометрические проекции подразделяются на:
— изометрические, когда все три коэффициента искажения одинаковы (kx=ky=kz);
— диметрические, когда коэффициенты искажения одинаковы по двум осям, а третий не равен им (kx= kz ≠ky);
— триметрические, когда все три коэффициенты искажения не равны между собой (kx≠ky≠kz).
В зависимости от направления проецирующих лучей аксонометрические проекции подразделяются на прямоугольные и косоугольные. Если проецирующие лучи перпендикулярны аксонометрической плоскости проекций, то такая проекция называется прямоугольной. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая. Если проецирующие лучи направлены под углом к аксонометрической плоскости проекций, то такая проекция называется косоугольной. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.
В прямоугольной изометрии углы между осями равны 120°. Действительный коэффициент искажения по аксонометрическим осям равен 0,82, но на практике для удобства построения показатель принимают равным 1. Вследствие этого аксонометрическое изображение получается увеличенным в 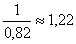
Изометрические оси изображены на рисунке 57.
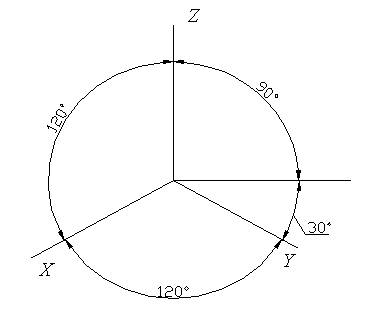
Рисунок 57
Построение изометрических осей можно выполнить при помощи циркуля (рисунок 58). Для этого сначала проводят горизонтальную линию и перпендикулярно к ней проводят ось Z. Из точки пересечения оси Z с горизонтальной линией (точка О) проводят вспомогательную окружность произвольным радиусом, которая пересекает ось Z в точке А. Из точки А этим же радиусом проводят вторую окружность до пересечения с первой в точках В и С. Полученную точку В соединяют с точкой О — получают направление оси Х. Таким же образом соединяют точку С с точкой О — получают направление оси Y.

Рисунок 58
Построение изометрической проекции шестиугольника представлено на рисунке 59. Для этого необходимо отложить по оси X радиус описанной окружности шестиугольника в обе стороны относительно начала координат. Затем, по оси Y отложить величину размера под ключ, из полученных точек провести линии параллельно оси X и отложить по ним величину стороны шестиугольника.
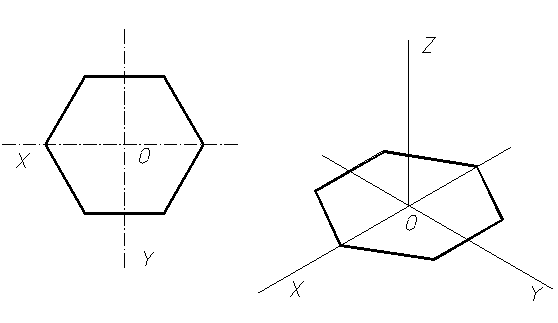
Рисунок 59
Построение окружности в прямоугольной изометрической проекции
Наиболее сложной плоской фигурой для вычерчивания в аксонометрии является окружность. Как известно, окружность в изометрии проецируется в эллипс, но построение эллипса довольно сложно, поэтому ГОСТ 2.317-69 рекомендует вместо эллипсов применять овалы. Существует несколько способов построения изометрических овалов. Рассмотрим один из наиболее распространенных.
Размер большой оси эллипса 1,22d, малой 0,7d, где d — диаметр той окружности, изометрия которой строится. На рисунке 60 показан графический способ определения большой и малой осей изометрического эллипса. Для определения малой оси эллипса соединяют точки С и D. Из точек С и D, как из центров, проводят дуги радиусов, равных СD, до взаимного их пересечения. Отрезок АВ — большая ось эллипса.
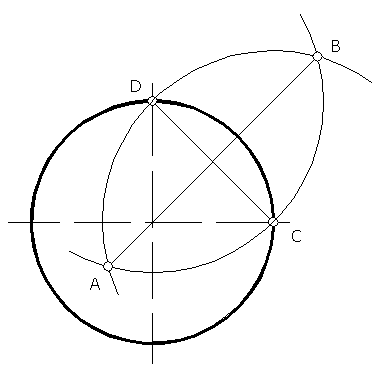
Рисунок 60
Установив направление большой и малой осей овала в зависимости от того, какой координатной плоскости принадлежит окружность, по размерам большой и малой оси проводят две концентрические окружности, в пересечении которых с осями намечают точки О1, О2, О3, О4, являющиеся центрами дуг овала (рисунок 61).
Для определения точек сопряжения проводят линии центров, соединяя О1, О2, О3, О4. из полученных центров О1, О2, О3, О4 проводят дуги радиусами R и R1. размеры радиусов видны на чертеже.
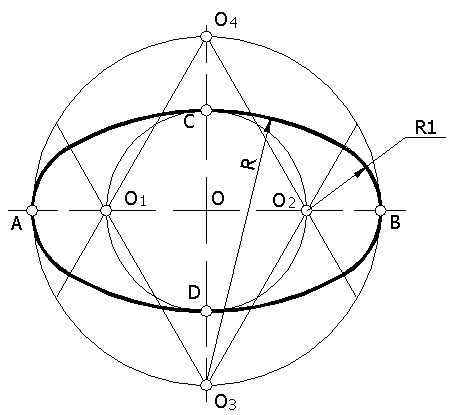
Рисунок 61
Направление осей эллипса или овала зависит от положения проецируемой окружности. Существует следующее правило: большая ось эллипса всегда перпендикулярна к той аксонометрической оси, которая на данную плоскость проецируется в точку, а малая ось совпадает с направлением этой оси (рисунок 62).
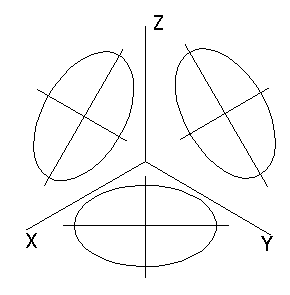
Рисунок 62
Штриховка и изометрической проекции
Линии штриховки сечений в изометрической проекции, согласно ГОСТ 2.317-69, должны иметь направление, параллельное или только большим диагоналям квадрата, или только малым.
Прямоугольной диметрией называется аксонометрическая проекция с равными показателями искажения по двум осям X и Z, а по оси Y показатель искажения в два раза меньше.
По ГОСТ 2.317-69 применяют в прямоугольной диметрии ось Z, расположенную вертикально, ось Х наклонную под углом 7°, а ось Y-под углом 41° к линии горизонта. Показатели искажения по осям X и Z равны 0,94, а по оси Y-0,47. Обычно применяют приведенные коэффициенты kx=kz=1, ky=0,5, т.е. по осям X и Z или по направлениям им параллельным, откладывают действительные размеры, а по оси Y размеры уменьшают в два раза.
Для построения осей диметрии пользуются способом, указанным на рисунке 63, который заключается в следующем:
На горизонтальной прямой, проходящей через точку О, откладывают в обе стороны восемь равных произвольных отрезков. Из конечных точек этих отрезков вниз по вертикали откладывают слева один такой же отрезок, а справа – семь. Полученные точки соединяют с точкой О и получают направление аксонометрических осей X и Y в прямоугольной диметрии.
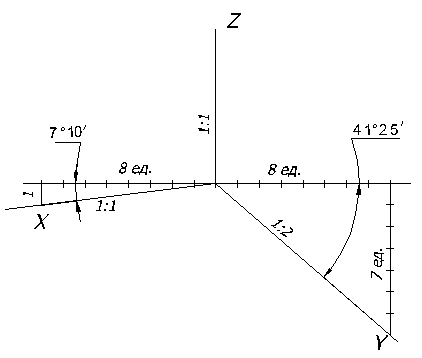
Рисунок 63
Построение диметрической проекции шестиугольника
Рассмотрим построение в диметрии правильного шестиугольника, расположенного в плоскости П1 (рисунок 64).
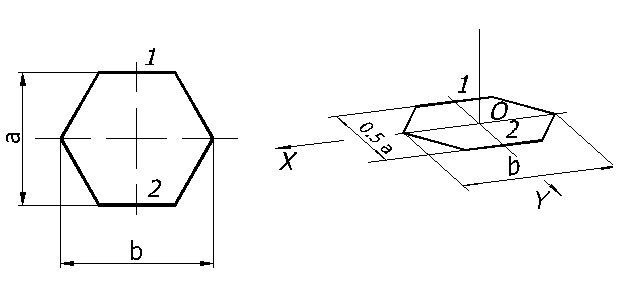
Рисунок 64
На оси Х откладываем отрезок равный величине b, чтобы его середина находилась в точке О, а по оси Y – отрезок а, размер которого уменьшен вдвое. Через полученные точки 1 и 2 проводим прямые параллельно оси ОХ, на которых откладываем отрезки равные стороне шестиугольника в натуральную величину с серединой в точках 1 и 2. Полученные вершины соединяем. На рисунке 65а изображен в диметрии шестиугольник, расположенный параллельно фронтальной плоскости, а на рисунке 66б -параллельно профильной плоскости проекции.
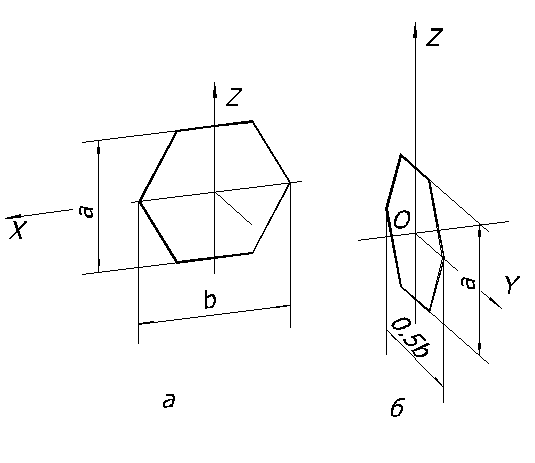
Рисунок 65
Построение окружности в диметрии
В прямоугольной диметрии все окружности изображаются эллипсами,
Длина большой оси для всех эллипсов одинакова и равна 1,06d. Величина малой оси различна: для фронтальной плоскости равна 0,95d , для горизонтальной и профильной плоскостей – 0,35 d.
На практике эллипс заменяется четырехцентровым овалом. Рассмотрим построение овала, заменяющего проекцию окружности, лежащей в горизонтальной и профильной плоскостях (рисунок 66).
Через точку О – начало аксонометрических осей, проводим две взаимно перпендикулярные прямые и откладываем на горизонтальной линии величину большой оси АВ=1,06d , а на вертикальной линии величину малой оси СD=0,35d. Вверх и вниз от О по вертикали откладываем отрезки ОО1 и ОО2, равные по величине 1,06d. Точки О1 и О2 являются центром больших дуг овала. Для определения еще двух центров (О3 и О4) откладываем на горизонтальной прямой от точек А и В отрезки АО3 и ВО4, равные ¼ величины малой оси эллипса, то есть 
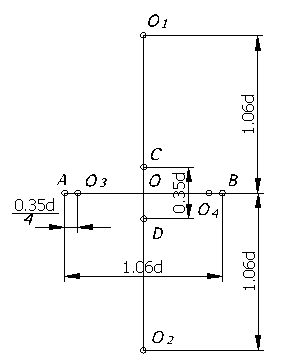
Рисунок 66
Затем, из точек О1 и О2 проводим дуги, радиус которых равен расстоянию до точек С и D, а из точек О3 и О4 – радиусом до точек А и В (рисунок 67).
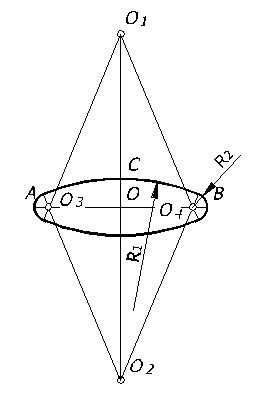
Рисунок 67
Построение овала, заменяющего эллипс, от окружности, расположенной в плоскости П2, рассмотрим на рисунке 68. Проводим оси диметрии: Х, Y, Z. Малая ось эллипса совпадает с направлением оси Y, а большая перпендикулярна к ней. На осях Х и Z от начала откладываем величину радиуса окружности и получаем точки M, N, K, L, являющиеся точками сопряжения дуг овала. Из точек M и N проводим горизонтальные прямые, которые в пересечении с осью Y и перпендикуляром к ней дают точки О1, О2, О3, О4 – центры дуг овала (рисунок 68).
Из центров О3 и О4 описывают дугу радиусом R2=О3 М, а из центров О1 и О2 — дуги радиусом R1= О2 N
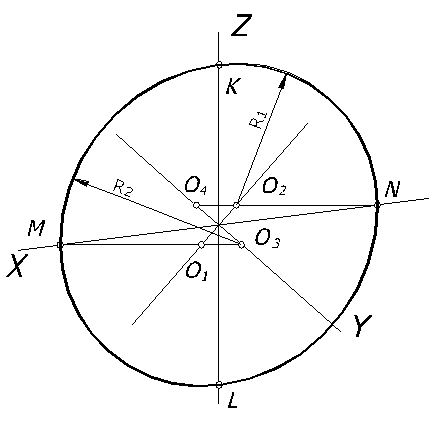
Рисунок 68
Штриховка а прямоугольной диметрии
Линии штриховки разрезов и сечений в аксонометрических проекциях выполняются параллельно одной из диагоналей квадрата, стороны которого расположены в соответствующих плоскостях параллельно аксонометрическим осям (рисунок 69).
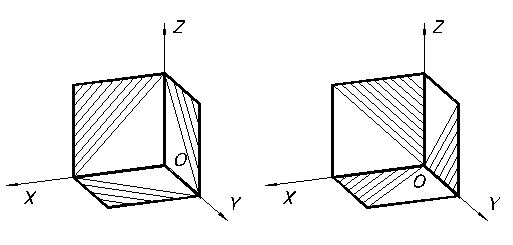
Рисунок 69
- Какие виды аксонометрических проекций вы знаете?
- Под каким углом расположены оси в изометрии?
- Какую фигуру представляет изометрическая проекция окружности?
- Как расположена большая ось эллипса для окружности, принадлежащей профильной плоскости проекций?
- Какие приняты коэффициенты искажения по осям X, Y, Z для построения диметрической проекции?
- Под какими углами расположены оси в диметрии?
- Какой фигурой будет являться диметрическая проекция квадрата?
- Как построить диметрическую проекцию окружности, расположенной во фронтальной проскости проекций?
- Основные правила нанесения штриховки в аксонометрических проекциях.
|