Функция графика четверти окружности (4 видео)

Четверть числовой окружности

Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть

Содержание

Почему так важно определять какой четверти принадлежит угол?
Про непостоянство четвертей:
Тригонометрия простыми словами
Значения тригонометрических функций для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Тригонометрический круг
Углы в радианах
Алгебра. Урок 5. Графики функций
Декартова система координат
Функция
Прямая
Парабола
Гипербола
Квадратный корень
Возрастающие/убывающие функции
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
📸 Видео

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Почему так важно определять какой четверти принадлежит угол?

Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .

Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.

Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.

Пример (ЕГЭ):

Нам известен косинус, а найти нужно синус того же угла. Какая тригонометрическая формула связывает синус и косинус того же угла?
Основное тригонометрическое тождество. Запишем его.

Подставим известное, и проведем вычисления.

Видео:Графики функций №5.ОкружностьСкачать

Про непостоянство четвертей:

Важно понимать, что, например, первой четверти принадлежат не только углы от (0) до (frac) , но и углы от (2π) до (frac) , и от (4π) до (frac) , и от (6π) до (frac) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.

Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.

((0;-) (frac) ()) — четвертая четверть

Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.

Видео:Как искать точки на тригонометрической окружности.Скачать

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:

Синус угла – отношение противолежащего катета к гипотенузе;
Косинус угла – отношение прилежащего катета к гипотенузе;
Тангенс угла – отношение противолежащего катета к прилежащему;
Котангенс угла – отношение прилежащего катета к противолежащему.

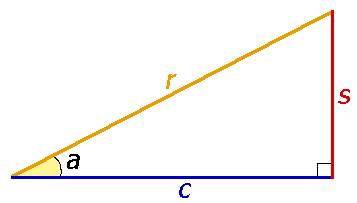Или в виде формул:

Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

0°

30°

45°

60°

90°

sin

√3

–

ctg

–

√3

Принцип повтора знаков тригонометрических функций

Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.

В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.

Например, значения тригонометрических функций для углов 270° и -90° равны.

Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Тригонометрический круг

Углы в радианах

Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан.

Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π .

Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.

Видео:ВСЁ ПРО ГРАФИКИ ЕГЭ 2024 (Прямая, Парабола, Окружность, Модуль, Гипербола, Корень, Области, Сдвиги)Скачать

Алгебра. Урок 5. Графики функций

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Декартова система координат

Функция

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Декартова система координат

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Видео:Уравнение окружности (1)Скачать

Функция

Функция – это отображение элементов множества X на множество Y . При этом каждому элементу x множества X соответствует одно единственное значение y множества Y .

Видео:Тригонометрическая окружность. Как выучить?Скачать

Прямая

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Важно : это уравнение не является функцией так как нарушается определение функции ( функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y ). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y . Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Видео:Тригонометрические функции и их знакиСкачать

Парабола

Графиком функции y = a x 2 + b x + c является парабола .

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :

Коэффициент a указывает на то, куда направлены ветки параболы.

Если a > 0 , ветки параболы направлены вверх.
Если a 0 , ветки параболы направлены вниз.

Коэффициент c указывает, в какой точке парабола пересекает ось y .
Коэффициент b помогает найти x в – координату вершины параболы.

Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

Если D > 0 – две точки пересечения.
Если D = 0 – одна точка пересечения.
Если D 0 – нет точек пересечения.

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Гипербола

Графиком функции y = k x является гипербола .

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>

Если k 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Квадратный корень

Функция y = x имеет следующий график:

Видео:Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать

Возрастающие/убывающие функции

Функция y = f ( x ) возрастает на интервале , если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале , если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции , находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции , находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Видео:В какой четверти пересекаются графики. #ShortsСкачать