Содержание

Глава 7. Изображение линий на чертежах
§ 41. Взаимное расположение двух прямых
Взаимное положение прямых
Взаимное положение прямых
🔍 Видео

Глава 7. Изображение линий на чертежах

Глава 7Образование линийКомплексные чертежи прямых линийРасположение прямой относительно плоскостей проекцийВзаимное расположение двух прямыхОпределение натуральной величины отрезка прямой линииКривые линииВзаимное расположение точки и линииВопросы

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

§ 41. Взаимное расположение двух прямых

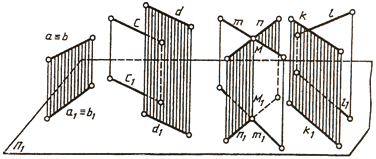
Две прямые пространства могут иметь различное расположение (рис. 74). Они могут совпадать а ≡ b, быть параллельными с ׀׀ d, пересекаться m ∩ n и скрещиваться (k°/l).

Если две прямые параллельны, то на комплексном чертеже (рис. 75, а) их одноименные проекции параллельны.

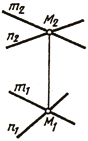
Если две прямые пересекаются в некоторой точке М, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи (рис. 75, б):

Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи (рис. 75, в):

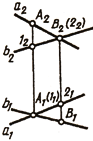
A₁ (1₁) — горизонтально конкурирующие точки;

B₂ (2₂) — фронтально конкурирующие точки.

В другом случае одна пара проекций будет пересекаться, а вторая может быть параллельными прямыми (рис. 75, г):

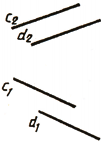
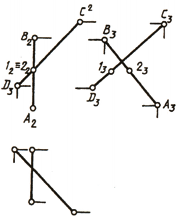
Следует обратить внимание на особые случаи определения взаимного расположения двух прямых в пространстве. Если одна из них (рис. 76, а) или обе (рис. 76, 6) окажутся профильными прямыми, то для определения взаимного расположения их необходимо построить третью, профильную проекцию этих прямых.

Если рассматривать рис. 76, а, можно ошибочно сделать предположение, что прямые АВ и CD пересекаются. Однако если построить профильные проекции этих прямых, станет видно, что они скрещиваются, так как точки 1 и 2 не совпадают, а являются фронтально конкурирующими точками.

Рассматривая рис. 76, б,можно ошибочно предположить, что прямые АВ и CD параллельны. Но после построения их профильных проекций увидим, что они скрещиваются, так как на этой плоскости проекции их пересекаются.

Две прямые, параллельные или пересекающиеся, могут иметь общую проецирующую плоскость (рис. 77, а).Тогда их изображения на соответствующую плоскость проекций совпадут. Такие прямые называют конкурирующими .

Прямые а и b горизонтально конкурирующие, имеют общую горизонтально проецирующую плоскость (рис. 77, б).

Прямые с и d (рис. 77, в) — фронтально конкурирующие, имеют общую фронтально проецирующую плоскость.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Взаимное положение прямых

Прямые линии в пространстве могут пересекаться, если имеют одну общую точку. Если две прямые линии пересекаются в бесконечности (несобственная точка), то они параллельны. Если две прямые линии не имеют общей точки, то они скрещиваются.

На рис. 5.27, а показано наглядное изображение двух пересекающихся прямых. Как видно из рис. 5.27, прямые с и Ъ имеют лишь одну общую точку К, которая называется точкой пересечения.

На рис. 5.27, б показан эпюр двух пересекающихся прямых с и Ъ в точке К. Анализируя данный комплексный чертеж, можно сформулировать признак пересекающихся прямых: две пересекающиеся прямые имеют проекции только одной точки, принадлежащей обеим прямым:

Таким образом, две пересекающиеся прямые на комплексном чертеже имеют проекции: а) пересекающихся прямых с проекциями общей точки пересечения (рис. 5.27, фронтальная и профильная проекции); б) одна из проекций изображается как одна линия (рис. 5.27, горизонтальная проекция).

Две прямые а и Ъ параллельны, если они пересекаются в бесконечности, т. е. имеют одну общую несобственную точку 1C (рис. 5.28).

На рис. 5.29, а показаны две параллельные прямые общего положения. Частный случай расположения прямых относительно плоскостей проекций, когда они располагаются в проецирующей плоскости. На рис. 5.29, б представлено наглядное изображение двух параллельных прямых а и Ь, расположенных в горизонтально проецирующей плоскости.

На комплексном чертеже проекции двух параллельных прямых изображаются в виде а) параллельных проекций (рис. 5.30, б), б) параллельных проекций и одной проекции, на которой проекции конкурируют (рис. 5.29, б):

Скрещивающиеся прямые — это прямые, не имеющие общей точки. Однако их проекции могут выглядеть как пересекающиеся (рис. 5.31) или параллельные прямые (рис. 5.32). В первом случае точка пересечения является проекцией конкурирующих точек 1 и 2 (рис. 5.31).

На комплексном чертеже в первом случае имеем две проекции пересекающихся в конкурирующих точках 1₂(2₂) и 3i(4i) прямых (рис. 5.33, а). Во втором — горизонтальные проекции параллельны, а фронтальные пересекаются в конкурирующих точках 1 и 2 (рис. 5.33, б).

Две скрещивающиеся прямые на комплексном чертеже могут изображаться а) в виде пересекающихся проекций (рис. 5.33, а), у которых имеются две пары проекций конкурирующих точек (1(2) — точка 1 видимая, и 3(4) — точка 3 видимая); б) одной проекцией в виде пересекающихся прямых с парой конкурирующих точек, а второй проекцией в виде параллельных прямых (рис. 5.33, б).

Задание: через точку К провести прямую т, пересекающую прямые а и Ъ (рис. 5.34, а).

Решение. Прямая т должна иметь общие точки с прямыми а и Ъ. Начинаем построение с горизонтальной плоскости проекций, так как прямая а — горизонтально проецирующая и точка пересечения (2) с прямой а будет совпадать с ее проекцией. Зная положение прямой т_< по линиям связи точки 11, определяем 1₂ и строим фронтальную проекцию прямой т (рис. 5.34, б) по точкам К₂ и 1₂.

Задание: определить расстояние между точкой С и прямой а (рис. 5.35, а).

Решение. Кратчайшее расстояние между точкой и прямой — перпендикуляр, опущенный из точки, на прямую. Угол 90° проецируется в натуральную величину, если одна из его сторон параллельна плоскости проекций, а вторая не перпендикулярна ей (теорема о прямом угле, свойство 8, п. 2.2.3).

Прямая а — горизонталь, так как ее фронтальная проекция горизонтальна (см. свойства горизонтали). Проекция перпендикуляра, опущенного из точки С на прямую а и будет соответствовать натуральной величине угла 90°, поскольку прямая а параллельна горизонтальной плоскости. Фронтальную проекцию точки В определим по линии связи (рис. 5.35, б).

Воспользуемся правилом прямоугольного треугольника и определим натуральную величину кратчайшего расстояния от точки С до прямой а — IBC1 (рис. 5.35, б).

Задание: через точку С (рис. 5.36, а) провести горизонталь h и фронталь/ пересекающие прямую а.

Решение. Две прямые пересекаются, если они имеют общую точку. Точка принадлежит прямой, если все ее проекции принадлежат соответствующим проекциям прямой (признак принадлежности точки прямой). Построение фронтали и горизонтали начинаем с той проекции, положение которой относительно осей координат известно: для горизонтали — h₂ (параллельно оси х), для фронтали —f (параллельно оси х).

По линиям связи находим проекции точек пересечения, принадлежащих обеим прямым уровня и прямой а: точка В для h и точка D для/(рис. 5.36, б).

Соединяем соответствующие проекции точек пересечения с проекциями точки С и получаем искомые проекции горизонтали и фронтали.

Задание: провести фронталь/ пересекающую прямые т, I и отрезок [.ЛВ] (рис. 5.37).

Решение. Положение горизонтальной проекции фронтальной прямой уровня может быть только горизонтально. Эта проекция однозначно должна проходить через проекцию прямой / в точке 2, т. е. через проекцию 1 (рис. 5.38). Далее по линии связи проекции точки li находим ее фронтальную проекцию — 1₂. Положение фронтальной проекции точки 2 (2₂) пока не известно. Ее определим, после того как проведем фронтальную проекцию фронтали f Для этого найдем фронтальную проекцию точки 3, построив подобные треугольники (пример 14). Соединяя точки 1₂ и 3₂, определяем положение точки 2₂.

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Взаимное положение прямых

Как известно, прямые в пространстве могут быть пересекающимися, параллельными или скрещивающимися. Рассмотрим эти случаи.

Пересекающиеся прямые. Наглядное изображение двух прямых АВ и CD. пересекающихся в точке К, приведено на рисунке 2.10, их чертеж в системе V, Н — на рисунке 2.11.

Если прямые пересекаются, то их одноименные проекции пересекаются между собой, а проекции точек пересечения лежат на одной линии связи.

Для прямых, кроме профильных, в системе V, Н справедливо и обратное утверждение:

если в системе V, Н тонки пересечения одноименных проекций прямых, кроме профильных, лежат на одной линии связи, то прямые пересекаются.

Если в системе V, Н одна из рассматриваемых прямых профильная, то, чтобы ответить на вопрос, пересекаются ли прямые, следует построить их профильные проекции.

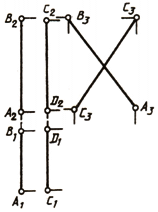
Примеры чертежей пересекающихся и непересекаюших- ся (скрещивающихся) прямых, из которых одна с проекциями a’b’, ab, а»Ь“— профильная, показаны на рисунках 2.12 и 2.13.

На рисунке 2.12 все три проекции к’, к, к» точки К прямой CD принадлежат и трем одноименным проекциям a’b’, ab и а»Ь» прямой АВ, т. е. прямые пересекаются.

На рисунке 2.13 профильная проекция Г точки L прямой CD не принадлежит профильной проекции а»Ь», следовательно, прямые АВ и CD не пересекаются (см. также рис. 2.7, а).

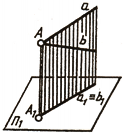
На рисунке 2.14 показаны прямые, две проекции которых пересекаются в одной точке, а две другие проекции сливаются в одну линию. Это означает, что обе прямые принадлежат плоскости Р, перпендикулярной плоскости Н (рис. 2.15).

Частный случай ортогональной проекции двух взаимно перпендикулярных прямых, из которых одна параллельна плоскости проекций, а другая не перпендикулярна ей, рассмотрен в § 1.3 (см. рис. 1.10).

Чертеж прямого угла АВС со стороной ВС, параллельной плоскости Я, приведен на рисунке 2.16. Горизонтальная проекция Ьа стороны ВА перпендикулярна горизонтальной проекции Ьс стороны ВС.

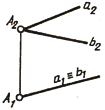
Эта особенность проецирования прямого угла упрощает решение ряда задач. Например, пусть требуется начертить перпендикуляр из точки с проекциями а’, а к прямой с проекциями Ь’с’, Ьс, параллельной плоскости V (рис. 2.17). Для этого из точки а‘ проводим перпендикуляр а’т’ к Ь’с’. Построив проекцию т, проводим горизонтальную проекцию am перпендикуляра.

Это свойство будет широко использовано в дальнейшем.

Заметим, что проекция любого угла в зависимости от положения его плоскости может представлять собой острый, прямой или тупой угол (или прямую линию, если плоскость угла перпендикулярна плоскости проекций). Если угол не прямой и одна сторона его параллельна плоскости проекций, то на эту плоскость острый угол проецируется также в виде острого угла меньшей величины, тупой угол — в виде тупого угла большей величины.

Параллельные прямые. Если в пространстве прямые параллельны, то их одноименные проекции параллельны между собой. Действительно (рис. 2.18), проецирующие плоскости Р и Q, проведенные через параллельные прямые АВ и CD, параллельны между собой. С плоскостью проекций Я они пересекаются по параллельным прямым ab и cd — проекциям прямых АВ и CD на плоскости Я. Однако из параллельности проекций не всегда следует параллельность прямых.

В примере на рисунке 2.19 проекции a’b’, e’f’, ab, ef профильных прямых АВ и EF между собой параллельны. Однако

зо из взаимного положения их профильных проекций видно, что сами прямые не параллельны.

Для прямых общего положения эти условия параллельности следующие:

если одноименные проекции прямых общего положения параллельны в системе двух плоскостей проекций, то прямые параллельны (рис. 2.20).

Для прямых частного положения:

если одноименные проекции прямых параллельны одной из осей проекций, то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой параллельны прямые.

По рисунку 2.21 заключаем, что профильные прямые 5—6 и 7—8 параллельны, так как параллельны их профильные проекции 5″ 6″ и 7″ 8″.

Скрещивающиеся прямые. Скрещивающиеся прямые не имеют общих точек. Наглядное изображение двух скрещивающихся прямых АВ и CD общего положения дано на рисунке 2.22, их чертеж — на рисунке 2.23. С точкой пересечения одноименных _Рис 2.21 проекций ab и cd (рис. 2.22) совпада

ют проекции к и / двух точек К и L, принадлежащих различным прямым CD и А В.

Точки пересечения одноименных проекций скрещивающихся прямых не лежат на одной линии связи (рис. 2.23).

Интересен вопрос: какая из изображенных на чертеже прямых выше другой или ближе другой к наблюдателю? Это определяют путем анализа положения определенных точек этих прямых.

На рисунке 2.22 видно, что при взгляде сверху по указанной стрелке точка L на прямой АВ закрывает точку К (проекция точки К на плоскости Я показана поэтому в скобках). Соответственно и на чертеже, приведенном на рисунке 2.23, видно, что фронтальная проекция Г выше фронтальной проекции к и при взгляде сверху по стрелке N при проецировании на плоскость Я точка L закрывает точку К (горизонтальная проекция к показана в скобках). На плоскости V совпадают фронтальные проекции Г и 2‘ точек прямых А В и CD. При взгляде спереди по стрелке М видно, что точка 1 прямой АВ

Рис. 2.22 Рис. 2.23

находится ближе к наблюдателю, и при проецировании на плоскость Кточка / прямой АВ закрывает точку 2 прямой CD (фронтальная проекция 2′ точки 2 показана в скобках).

Рассмотренные точки скрещивающихся прямых, проекции которых на одной из плоскостей совпадают, в литературе иногда называют конкурирующими точками.

01. При каком положении относительно плоскостей проекций прямую называют прямой общего положения?
2. Как выражается соотношение между проекцией отрезка прямой и самим отрезком?
3. Как расположена прямая в системе Н, V, W если все три проекции отрезка этой прямой равны между собой?
4. Как построить профильную проекцию отрезка прямой общего положения по данным фронтальной и горизонтальной проекциям?
5. Как располагается фронтальная проекция отрезка прямой линии, если его горизонтальная проекция равна самому отрезку?
6. Как располагается горизонтальная проекция отрезка прямой линии, если его фронтальная проекция равна самому отрезку?
7. Как разделить на чертеже отрезок прямой линии в заданном отношении?
8. Как построить на чертеже треугольники для определения длины отрезка прямой линии общего положения и ее углов с горизонтальной и фронтальной плоскостями проекций?
9. Какое свойство параллельного проецирования относится к параллельным прямым?
10. Можно ли по фронтальной и горизонтальной проекциям двух профильных прямых определить, параллельны ли между собой эти прямые?
11. Как следует истолковать точку пересечения проекций двух скрещивающихся прямых?
12. В каком случае прямой угол проецируется в виде прямого угла?