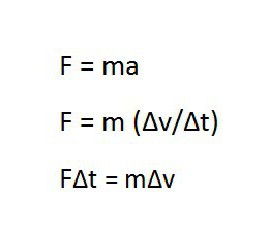Физика и математика не обходятся без понятия «векторная величина». Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.
- Как отличить скалярную величину от векторной?
- Какие действия чаще всего выполняются с векторами?
- Какие векторы изучают в физике?
- Первая величина — скорость
- Вторая величина — сила
- Третья величина — перемещение
- Четвертая величина — ускорение
- Пятая величина — импульс
- Задача о неупругом ударе
- Задача с разделением тела на части
- Задача про выстрел под углом
- Задача о переправе через реку
- Как избавиться от вектора физика
- Как избавиться от вектора физика
- 📸 Видео
Видео:Векторы в физике. Что нужно знать? | 50 уроков физики (2/50)Скачать

Как отличить скалярную величину от векторной?
Первая всегда имеет только одну характеристику. Это ее числовое значение. Большинство скалярных величин могут принимать как положительные, так и отрицательные значения. Их примерами может служить электрический заряд, работа или температура. Но есть такие скаляры, которые не могут быть отрицательными, например, длина и масса.
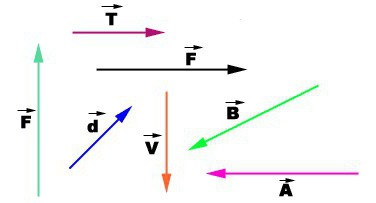
Векторная величина, кроме числовой величины, которая всегда берется по модулю, характеризуется еще и направлением. Поэтому она может быть изображена графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенную сторону.
При письме каждая векторная величина обозначается знаком стрелки на буквой. Если идет речь о числовом значении, то стрелка не пишется или ее берут по модулю.
Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Какие действия чаще всего выполняются с векторами?
Сначала — сравнение. Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.
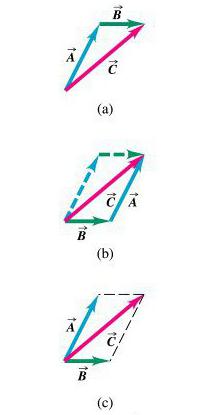
Потом идет сложение. Его можно сделать по двум правилам: треугольника или параллелограмма. Первое предписывает откладывать сначала один вектор, потом от его конца второй. Результатом сложения будет тот, который нужно провести от начала первого к концу второго.
Правило параллелограмма можно использовать, когда нужно сложить векторные величины в физике. В отличие от первого правила, здесь их следует откладывать от одной точки. Потом достроить их до параллелограмма. Результатом действия следует считать диагональ параллелограмма, проведенную из той же точки.
Если векторная величина вычитается из другой, то они снова откладываются из одной точки. Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.
Видео:Физика | Ликбез по векторамСкачать

Какие векторы изучают в физике?
Их так же много, как скаляров. Можно просто запомнить то, какие векторные величины в физике существуют. Или знать признаки, по которым их можно вычислить. Тем, кто предпочитает первый вариант, пригодится такая таблица. В ней приведены основные векторные физические величины.
| Обозначение в формуле | Наименование |
| v | скорость |
| r | перемещение |
| а | ускорение |
| F | сила |
| р | импульс |
| Е | напряженность электрического поля |
| В | магнитная индукция |
| М | момент силы |
Теперь немного подробнее о некоторых из этих величин.
Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Первая величина — скорость
С нее стоит начать приводить примеры векторных величин. Это обусловлено тем, что ее изучают в числе первых.
Скорость определяется как характеристика движения тела в пространстве. Ею задается числовое значение и направление. Поэтому скорость является векторной величиной. К тому же ее принято разделять на виды. Первый является линейной скоростью. Ее вводят при рассмотрении прямолинейного равномерного движения. При этом она оказывается равной отношению пути, пройденного телом, ко времени движения.
Эту же формулу допустимо использовать при неравномерном движении. Только тогда она будет являться средней. Причем интервал времени, который необходимо выбирать, обязательно должен быть как можно меньше. При стремлении промежутка времени к нулю значение скорости уже является мгновенным.
Если рассматривается произвольное движение, то здесь всегда скорость — векторная величина. Ведь ее приходится раскладывать на составляющие, направленные вдоль каждого вектора, направляющего координатные прямые. К тому же определяется он как производная радиус-вектора, взятая по времени.
Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Вторая величина — сила
Она определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Поскольку сила — векторная величина, то она обязательно имеет свое значение по модулю и направление. Так как она действует на тело, то важным является еще и точка, к которой приложена сила. Чтобы получить наглядное представление о векторах сил, можно обратиться к следующей таблице.
| Сила | Точка приложения | Направление |
| тяжести | центр тела | к центру Земли |
| всемирного тяготения | центр тела | к центру другого тела |
| упругости | место соприкосновения взаимодействующих тел | против внешнего воздействия |
| трения | между соприкасающимися поверхностями | в сторону, противоположную движению |
Также еще векторной величиной является равнодействующая сила. Она определяется как сумма всех действующих на тело механических сил. Для ее определения необходимо выполнить сложение по принципу правила треугольника. Только откладывать векторы нужно по очереди от конца предыдущего. Результатом окажется тот, который соединяет начало первого с концом последнего.
Видео:Вектор в Физике. Как Рисовать Вектор? Модуль Вектора || Урок Физики 8 класс // Подготовка к ЕГЭСкачать

Третья величина — перемещение
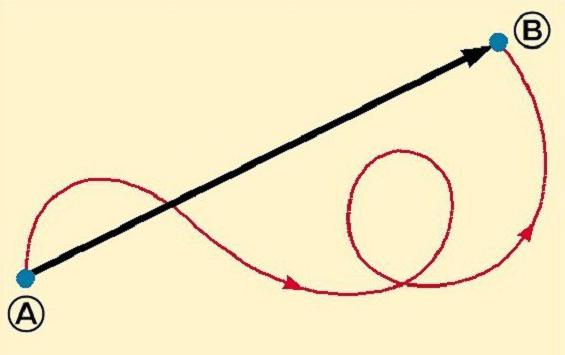
Во время движения тело описывает некоторую линию. Она называется траекторией. Эта линия может быть совершенно разной. Важнее оказывается не ее внешний вид, а точки начала и конца движения. Они соединяются отрезком, который называется перемещением. Это тоже векторная величина. Причем оно всегда направлено от начала перемещения к точке, где движение было прекращено. Обозначать его принято латинской буквой r.
Здесь может появиться такой вопрос: «Путь — векторная величина?». В общем случае это утверждение не является верным. Путь равен длине траектории и не имеет определенного направления. Исключением считается ситуация, когда рассматривается прямолинейное движение в одном направлении. Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.
Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Четвертая величина — ускорение
Оно является характеристикой быстроты изменения скорости. Причем ускорение может иметь как положительное, так и отрицательное значение. При прямолинейном движении оно направлено в сторону большей скорости. Если перемещение происходит по криволинейной траектории, то вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.
Выделяют среднее и мгновенное значение ускорения. Первое следует рассчитывать как отношение изменения скорости за некоторый промежуток времени к этому времени. При стремлении рассматриваемого интервала времени к нулю говорят о мгновенном ускорении.
Видео:Построение проекции вектора на осьСкачать

Пятая величина — импульс
По-другому его еще называют количеством движения. Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.
По определению последний равен произведению массы тела на скорость. Используя понятие импульса тела, можно по-другому записать известный закон Ньютона. Получается, что изменение импульса равно произведению силы на промежуток времени.
В физике важную роль имеет закон сохранения импульса, который утверждает, что в замкнутой системе тел ее суммарный импульс является постоянным.
Мы очень кратко перечислили, какие величины (векторные) изучаются в курсе физики.
Видео:Как проецировать вектора за 1 минуту?! | ЕГЭ по физике | Саня Эбонит | 100балльный репетиторСкачать

Задача о неупругом ударе
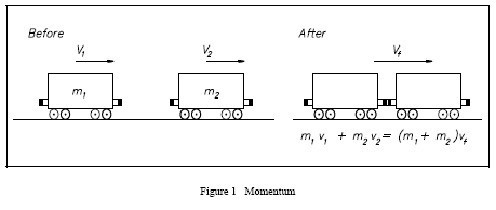
Условие. На рельсах стоит неподвижная платформа. К ней приближается вагон со скоростью 4 м/с. Массы платформы и вагона — 10 и 40 тонн соответственно. Вагон ударяется о платформу, происходит автосцеп. Необходимо вычислить скорость системы «вагон-платформа» после удара.
Решение. Сначала требуется ввести обозначения: скорость вагона до удара — v1, вагона с платформой после сцепки — v, масса вагона m1, платформы — m2. По условию задачи необходимо узнать значение скорости v.
Правила решения подобных заданий требуют схематичного изображения системы до и после взаимодействия. Ось OX разумно направить вдоль рельсов в ту сторону, куда движется вагон.
В данных условиях систему вагонов можно считать замкнутой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, а трение о рельсы не учитывается.
Согласно закону сохранения импульса, их векторная сумма до взаимодействия вагона и платформы равна общему для сцепки после удара. Сначала платформа не двигалась, поэтому ее импульс был равен нулю. Перемещался только вагон, его импульс — произведение m1 и v1.
Так как удар был неупругий, то есть вагон сцепился с платформой, и дальше он стали катиться вместе в ту же сторону, то импульс системы не изменил направления. Но его значение стало другим. А именно произведением суммы массы вагона с платформой и искомой скорости.
Можно записать такое равенство: m1 * v1 = (m1 + m2) * v. Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m1 * v1 / (m1 + m2).
По правилам следует перевести значения для массы из тонн в килограммы. Поэтому при подстановке их в формулу следует сначала умножить известные величины на тысячу. Простые расчеты дают число 0,75 м/с.
Ответ. Скорость вагона с платформой равна 0,75 м/с.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Задача с разделением тела на части
Условие. Скорость летящей гранаты 20 м/с. Она разрывается на два осколка. Масса первого 1,8 кг. Он продолжает двигаться в направлении, в котором летела граната, со скоростью 50 м/с. Второй осколок имеет массу 1,2 кг. Какова его скорость?
Решение. Пусть массы осколков обозначены буквами m1 и m2. Их скорости соответственно будут v1 и v2. Начальная скорость гранаты — v. В задаче нужно вычислить значение v2.
Для того чтобы больший осколок продолжал двигаться в том же направлении, что и вся граната, второй должен полететь в обратную сторону. Если выбрать за направление оси то, которое было у начального импульса, то после разрыва большой осколок летит по оси, а маленький — против оси.
В этой задаче разрешено пользоваться законом сохранения импульса из-за того, что разрыв гранаты происходит мгновенно. Поэтому, несмотря на то что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его значением по модулю.
Сумма векторных величин импульса после разрыва гранаты равна тому, который был до него. Если записать закон сохранения импульса тела в проекции на ось OX, то он будет выглядеть так: (m1 + m2) * v = m1 * v1 — m2 * v2. Из него просто выразить искомую скорость. Она определится по формуле: v2 = ((m1 + m2) * v — m1 * v1) / m2. После подстановки числовых значений и расчетов получается 25 м/с.
Ответ. Скорость маленького осколка равна 25 м/с.
Видео:Векторы и действия над ними, проекция вектора на координатные оси. Практическая часть. 9 класс.Скачать
Задача про выстрел под углом
Условие. На платформе массой M установлено орудие. Из него производится выстрел снарядом массой m. Он вылетает под углом α к горизонту со скоростью v (данной относительно земли). Требуется узнать значение скорости платформы после выстрела.
Решение. В этой задаче можно использовать закон сохранения импульса в проекции на ось OX. Но только в том случае, когда проекции внешних равнодействующих сил равна нулю.
За направление оси OX нужно выбрать ту сторону, куда полетит снаряд, и параллельно горизонтальной линии. В этом случае проекции сил тяжести и реакции опоры на OX будут равны нулю.
Задача будет решена в общем виде, так как нет конкретных данных для известных величин. Ответом в ней является формула.
Импульс системы до выстрела был равен нулю, поскольку платформа и снаряд были неподвижны. Пусть искомая скорость платформы будет обозначена латинской буквой u. Тогда ее импульс после выстрела определится как произведение массы на проекцию скорости. Так как платформа откатится назад (против направления оси OX), то значение импульса будет со знаком минус.
Импульс снаряда — произведение его массы на проекцию скорости на ось OX. Из-за того, что скорость направлена под углом к горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквенном равенстве это будет выглядеть так: 0 = — Mu + mv * cos α. Из нее путем несложных преобразований получается формула-ответ: u = (mv * cos α) / M.
Ответ. Скорость платформы определяется по формуле u = (mv * cos α) / M.
Видео:❗️ БИТКОИН ПОСЛЕ ETF. АЛЬТСЕЗОН НАЧАЛСЯСкачать

Задача о переправе через реку
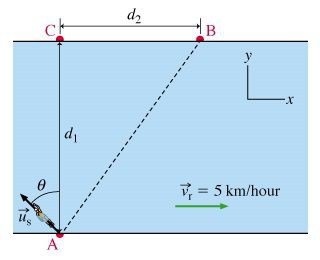
Условие. Ширина реки по всей ее длине одинакова и равна l, ее берега параллельны. Известна скорость течения воды в реке v1 и собственная скорость катера v2. 1). При переправе нос катера направлен строго к противоположному берегу. На какое расстояние s его снесет вниз по течению? 2). Под каким углом α нужно направить нос катера, чтобы он достиг противоположного берега строго перпендикулярно к точке отправления? Сколько времени t потребуется на такую переправу?
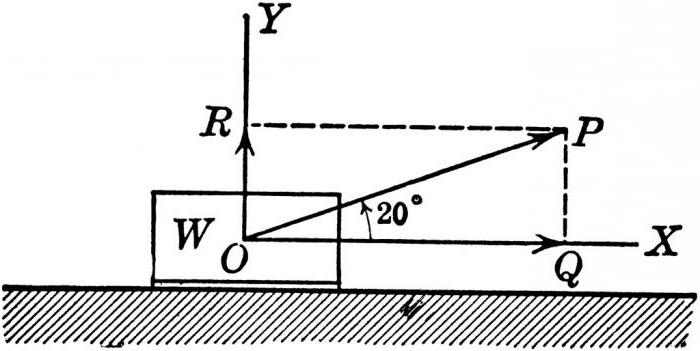
Решение. 1). Полная скорость катера является векторной суммой двух величин. Первая из них течение реки, которое направлено вдоль берегов. Вторая — собственная скорость катера, перпендикулярная берегам. На чертеже получается два подобных треугольника. Первый образован шириной реки и расстоянием, на которое сносит катер. Второй — векторами скоростей.
Из них следует такая запись: s / l = v1 / v2. После преобразования получается формула для искомой величины: s = l * (v1 / v2).
2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться вектор собственной скорости, равен отношению модулей v1 и v2. Для расчета времени движения потребуется разделить ширину реки на сосчитанную полную скорость. Значение последней вычисляется по теореме Пифагора.
Видео:Линейная зависимость и линейная независимость векторов.Скачать

Как избавиться от вектора физика
Задачи по физике — это просто!
Элементарные задачи из курса школьной физики.
Векторы в физике
Многие физические величины зависят от направления и называются векторными, например, скорость, перемещение, ускорение.
При работе с векторами (векторными величинами) существуют специальные обозначения, которые надо запомнить:
Изображение вектора на чертеже:
Если вектор параллелен координатной оси, то модуль вектора равен модулю проекции вектора на эту ось:
Проекция вектора может быть положительной или отрицательной (в зависимости от его положения относительно оси координат):
Если вектор перпендикулярен оси, то проекция вектора на эту ось равна нулю!
Как бы ни был направлен вектор, его модуль всегда можно рассчитать по формуле:
Сложение векторов (а это часто приходится выполнять в задачах) можно производить графически двумя способами — треугольника и параллелограмма.
Расчетные формулы прямолинейного равномерного движения
Расчетные формулы для прямолинейного равномерного движения — это формулы в проекциях векторов на координатную ось.
Скорость тела:

где
Vx — проекция вектора скорости на координатную ось х
Sx — проекция вектора перемещения на ось х
t — время, за которое совершается данное перемещение
Координата тела в любой момент времени
или после подстановки скорости:
Последнюю формулу иначе называют уравнением прямолинейного равномерного движения:
xo — начальная координата тела
x — конечная координата тела через время t после начала движения
Расстояние между движущимися телами при прямолинейном равномерном движении в любой момент времени:
l — расстояние между телами в любой момент времени движения
x1 — конечная координата первого тела на момент определения расстояния между телами
x2 — конечная координата второго тела на момент определения расстояния между телами
Видео:Все типы 2 задание векторы ЕГЭ по математике профиль 2024Скачать

Как избавиться от вектора физика
Из предыдущего параграфа мы знаем, что есть скалярные физические величины и есть векторные физические величины. Например, скорость – вектор, перемещение — вектор. Длина пути – скаляр (просто одно число с размерностью расстояния). А перемещение имеет длину и направление. Поэтому, это вектор. В трехмерной прямоугольной системе координат вектор перемещения можно определить, как тройку чисел, компонентов вектора по осям X , Y , Z . Эта тройка чисел однозначно задает направление и величину вектора перемещения.
Для чего нам понадобились вектора? И какие операции можно производить с векторами? И все-таки, любая ли тройка чисел задает вектор?
Для начала, чтобы нагляднее представить себе, что можно делать с векторами, будем представлять себе все вектора, как операции перемещения в пространстве. Операции, которые задаются тройкой чисел (компонентов). Такие операции можно применить к любой точке пространства (обобщенно, к любому физическому телу).
Сразу становятся понятны операции сложения и вычитания векторов. Просто последовательно применяем к точке один вектор, потом другой. Понятно, почему можно изменить порядок слагаемых и сумма (общее перемещение) не изменится. Понятно, что вычитание – есть прибавление вектора с обратным знаком (меняем направление стрелки).
Для всех векторов это справедливо! Но что особенно важно – это справедливо для всех векторных функций.
Если у нас есть две векторные функции
Удобство применения векторов прежде всего заключается в краткости и понятности записи формул.
Например, материальная точка, движется по произвольной кривой в трехмерном пространстве с осями координат X , Y , Z .
где векто р ∆r = r(t1) – r(t 0 ) – есть вектор перемещения.
Приведенная выше векторная формула для скорости материальной точки в трехмерном пространстве означает, что
Вместо определенного момента t 0 мы можем выбрать произвольный момент времени t . И рассматривать функцию r ( t ) – векторную функцию зависимости координат от времени для случая трехмерного пространства. В общем случае неважно сколько размерностей в рассматриваемом нами пространстве – хоть две, хоть двадцать две. Одномерный случай – это тоже просто частный случай нашей векторной формулы. Вот чем удобны вектора!
Тогда v(t) — векторная функция зависимости мгновенной скорости нашего тела от времени
Где и запись с точками и запись дробью с буквой d — это всего лишь формы записи второй производной по времени. Просто векторную функцию r(t) продифференцировали два раза. После первого дифференцирования нашли первую производную – это функция скорости. После второго дифференцирования нашли вторую производную, которая есть функция зависимости ускорения от времени.
В обратном порядке a ( t ), v ( t ), r ( t ) – каждая следующая есть «первообразная» предыдущей. Напомним, операция, обратная дифференцированию, называется операцией интегрирования (или нахождения первообразной функции). Скажем упрощенно, нахождению функции, которая была до операции по ее дифференцированию.
Теперь, когда мы начали понимать физический смысл некоторых векторных функций, продолжим рассматривать другие операции, которые возможно выполнять с векторами.
Пусть у нас есть два вектора. F – вектор силы, действующей на материальную точку (Напомним: «материальная точка» — тело, имеющее массу, размерами которого можно пренебречь в данной задаче). И S – вектор перемещения нашей материальной точки под действием силы F .
Мы знаем, что работа (та, которая сила, умноженная на перемещение вдоль силы, или, по-другому, перемещение, умноженное на силу вдоль перемещения, или просто сила, умноженная на перемещение в одномерном случае) в нашем трехмерном «векторном» случае будет равняться скалярному произведению вектора силы на вектор перемещения материальной точки под действием этой силы.
Мы с вами помним из школьного курса физики, что механическая работа в общем случае равна модулю вектора силы, умноженному на модуль вектора перемещения и умноженному на косинус угла между векторами силы и перемещения.
В случае, если вектора силы и перемещения заданы в виде троек компонентов векторов по соответствующим осям прямоугольной системы координат, гораздо проще, чем вычислять модули и косинус угла между векторами, прямо посчитать работу по формуле скалярного произведения векторов. Это просто сумма произведений соответствующих компонент.
В физическом смысле, мы просто складываем между собой три работы (по каждой из осей отдельно как бы своя работа). Это возможно (складывать компоненты работы по разным осям) только в случае, когда эти компоненты скаляры. Мы не будем вдаваться в подробное доказательство. Отошлем читателя за подробностями в интернет.
Просто запомним формулу (67) и смысл скалярного произведения векторов.
Очень важное замечание!
Здесь и в дальнейшем (и в предыдущем изложении) мы всегда рассматриваем «Правую» систему координат.
Если вправо направить ось X , вверх ось Y , то ось Z будет как бы входить в нас (идти в положительном направлении на нас, а не от нас). Это очень важно никогда не забывать. В противном случае в формулах будут ошибки. И особенно большая путаница будет при изучении электромагнетизма с его правыми и левыми руками.
Правая система координат! Берем правую руку. Раскрываем ладонь перед собой. Оттопыриваем большой палец – это положительное направление оси X . Четыре пальца перпендикулярных большому показывают положительное направление оси Y . Тогда из открытой ладони прямо на вас перпендикулярно осям X , Y будет выходить положительное направление оси Z .
Необходимо запомнить и никогда не путать!
Теперь возьмем нашу правую систему координат и зададим три единичных вектора, по одному вдоль каждой из осей.
Тогда любой вектор A = (А x , Ay , Az ) можно записать в виде суммы трех векторов
Легко заметить, что скалярные произведения наших единичных векторов
Эта удобная тройка векторов очень пригодится нам в дальнейшем.
Теперь напомним, любую ли тройку чисел можно считать вектором? Или по-другому, любую ли тройку функций ( f x ( t ), fy ( t ), fz ( t )) можно назвать векторной функцией f ( t ) ?
Нет, не любую! А только если модуль значения и пространственное направление не меняется при повороте и перемещении системы координат. (И при переходе из одной системы координат к другой тоже)
Это очень важно!
Вектора при переходе от одной системы координат к другой не меняются.
И результаты векторных операций при переходе от одной системы координат к другой так же не меняются!
Какие еще есть операции над векторами?
Существует еще операция, называемая «векторное произведение» векторов
«Ну и ну! Как это? Для чего?»
Все очень просто!
Для начала убедимся, что векторные произведения наших единичных векторов между собой:
Поиграв с единичными векторами, вы наверняка уже догадались, что векторное произведение двух векторов дает в результате вектор, перпендикулярный плоскости, в которой лежат вектора сомножители, а по модулю равный площади параллелограмма, ограниченного векторами сомножителями. Как на рисунке ниже, где вектора сомножители i и s расположили в плоскости X , Y и один из них расположили вдоль оси X .
Хотя, правильнее сказать, что систему координат расположили таким образом. А мы помним, результат не зависит от выбора системы координат.
Поэтому, всегда во всех задачах мы выбираем систему координат так, как нам удобно!
Итак, зачем нужна операция векторного произведения векторов, определенная выше? Рассмотрим задачу «о рычагах». Пусть у нас есть твердое тело, представляющее из себя систему из трех стержней, жестко скрепленных в одной точке. И эта точка закреплена в пространстве так, что она является центром вращения («точка закрепления шарнира»). Как на рисунке ниже.
Имеем три вектора r1 , r2 , r3 , выходящих из точки в которой мы расположим начало нашей системы координат – точки (0,0,0).
К концам стержней приложили силы F1 , F2 , F3 . Силы создают вектора моментов сил – «крутящие моменты», приложенные к нашему твердому телу.
Момент силы — это модуль вектора момента силы. Синонимы вектора момента силы: крутящий момент, вращательный момент, вертящий момент, вращающий момент).
Наглядно представить себе вектор момента силы можно следующим образом: Представьте себе юлу (детскую игрушку «волчок»). Чем сильнее мы его закрутим за ось, тем быстрее и дольше он вращается. Закрепим ось волчка на какой-то прямой так, чтобы она могла свободно вращаться. Представьте теперь, что вы будете тянуть за тело волчка, стараясь повернуть его вокруг закрепленной оси. А ваш товарищ будет пытаться удержать ось рукой. Представили?
Будет ли волчок поворачиваться вокруг оси? И если вы будете тянуть его в одну сторону, а ваш товарищ в другую, то в какую сторону будет поворачиваться волчок? В ту, чья сила больше? Не совсем. Представим ситуацию на картинке. Вы взялись ближе к оси, а ваш товарищ взялся за диск. Если ось достаточно тонкая, а диск достаточно большой, то как бы вы ни старались, волчок будет поворачиваться в сторону вашего товарища. Хотя силу вы приложите гораздо большую, чем он.
«Рычаг», скажете вы. И будете правы! Задача о рычагах по сути аналогична. И решается она очень просто с использованием операции векторного произведения, которую мы с вами рассмотрели выше.
Из формул (74) — (76) мы знаем, что векторное произведение двух векторов есть вектор, который по направлению перпендикулярен плоскости, в которой лежат вектора сомножители. Величину этого вектора по модулю можно вычислить с учетом формул (71) – (73), а модуль вычисляется по простой формуле:
Так вот, вектор момента силы, приложенной к телу, равен векторному произведению радиус-вектора точки приложения силы умноженному на вектор силы. Начало координат выбирается в точке закрепления тела на шарнире (например, в точке подвеса перекладины рычажных весов). То есть начало координат всегда берем в точке, относительно которой тело может поворачиваться.
Складывая вектора моментов всех приложенных к телу сил мы автоматически находим результирующий вектор, который и определяет в какую сторону и насколько интенсивно будет вращаться тело, показанное на рисунке 9 выше.
Просто складываем три вектора момента, от каждой из сил. Если сумма равна нулю, то наше твердое тело «стоит на месте». Если не равна нулю, то наше тело имеет ненулевой момент сил относительно «точки подвеса» в плоскости, перпендикулярной нашему вектору суммы моментов M . И с угловым ускорением, которое пропорционально модулю этого вектора.
Можно обобщить задачу на произвольное твердое тело с закрепленной в пространстве точкой подвеса и неограниченным количеством приложенных сил, как показано на рисунке.
Оно будет вращаться относительно оси, в которой лежит наш результирующий вектор момента сил. И вращение будет тем интенсивнее, чем больше этот результирующий вектор по модулю. Направление вращения будет зависеть от направления этого вектора. Направлен в одну сторону, вращается тело в одну сторону, направлен в другую, тело вращается в обратную.
Причем, если тело закрепить на оси, как в случае рассмотренного нами волчка, то задача становится двумерной. Вращение может быть только относительно оси и, соответственно, можно рассматривать моменты сил, только в системе координат, перпендикулярной оси. Это мы рассмотрим в дальнейшем.
Вопрос: каково условие невращения твердого тела в общем случае, показанном на рисунке 11? Другими словами, при каких условиях общий (суммарный) момент вращения тела равен нулю?
Ответ: Если сумма моментов всех сил равна нулю, то тело находится во «вращательном равновесии» — т.е. не имеет суммарного момента вращения.
Эта задача – более общая по отношению к школьной задаче о рычагах, изображенной на рисунке 24.
Благодаря определенной нами операции векторного произведения векторов задача решается в одно действие.
Ответ: Условие отсутствия вращающего момента тела
Так как согласно условиям рисунка 13:
Тогда с учетом формул (70) – (72) получаем:
Получаем условия равновесия наших рычажных весов:
Получаем знакомое из школьного учебника соотношение:
Можно решать сразу в векторной форме:
Можно ли сократить вектор ускорения свободного падения в уравнении (101) из обеих частей уравнения?
Потому, что для этого нужно обе части уравнения «разделить» на вектор g .
А операции векторного деления не существует!
Внимание! При оперировании векторами всегда нужно помнить, что мы можем применять к векторным уравнениям только существующие векторные операции!
Распишем покомпонентно наше векторное уравнение (101) в соответствии с формулами для векторного произведения (74) – (76). Заметим, что мы «правильно» расположили нашу систему координат таки образом, чтобы уравнения были проще. В результате этого в векторном уравнении (101) только составляющие векторов по оси Z не равны нулю. Таким образом остается только найти условие при котором:
Получили скалярное уравнение, которое можно сократить:
Заметим, что модули r 1 и r 2 – это, по сути, координаты точек подвеса грузов m1 и m2 относительно начала оси X , которое (точку x = 0 ) мы выбрали в точке крепления шарнира рычага. Для того, чтобы выполнялось условие равновесия (107), r 1 и r 2 должны быть разных знаков
Что же означает эта, теперь уже скалярная, формула равновесия рычага?
1. Координаты расположения точек подвеса грузов должны быть расположены по разные стороны от точки шарнира рычага.
2. Массы подвешенных грузов должны быть обратно пропорциональны расстояниям от точки подвеса поперечины до точек подвеса грузов. Или по-другому – длина рычагов должна быть обратно пропорциональна массам подвешенных грузов.
📸 Видео
Урок 9. Проекции вектора на координатные осиСкачать

Лекция 5. Сложение и вычитание векторов │ФИЗИКА С НУЛЯ теорияСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

СУММА ВЕКТОРОВ правило треугольникаСкачать

Вычитание векторов. 9 класс.Скачать

Векторы для чайников (что потребуется знать при решении физических задач)Скачать