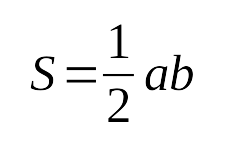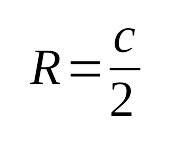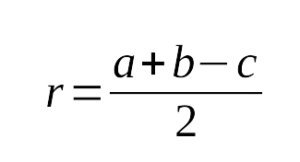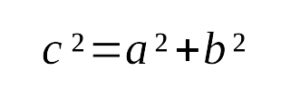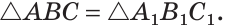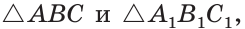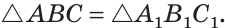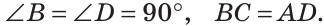- Определение
- Свойства прямоугольного треугольника
- Признаки равенства прямоугольных треугольников
- Признаки прямоугольного треугольника
- Признаки подобия прямоугольных треугольников
- Признаки равенства прямоугольных треугольников с примерами решения
- Второй признак (по катету и прилежащему острому углу)
- Третий признак (по катету и противолежащему острому углу)
- Четвертый признак (по гипотенузе и острому углу)
- Пятый признак (по катету и гипотенузе).
- Признаки равенства прямоугольных треугольников
- Теорема
- Доказательство
- Теорема
- Доказательство
- 📸 Видео
Видео:Геометрия 7. Урок 9 - Признаки равенства прямоугольных треугольниковСкачать

Определение
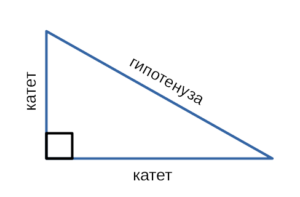
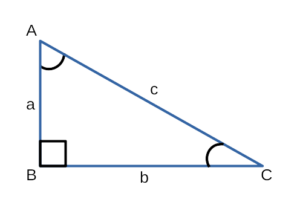
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.
Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.
Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.
Видео:7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать

Свойства прямоугольного треугольника
В прямоугольном треугольнике:
- Сумма острых углов 90˚.
- Катет, противолежащий углу в 30˚, равен половине гипотенузы.
- Медиана, проведенная к гипотенузе, равна ее половине.
- Центр описанной окружности — середина гипотенузы.
Формулы:
- Площадь прямоугольного треугольника равна
половине произведения катетов: - Радиус описанной окружности около прямоугольного
треугольника равен половине гипотенузы: - Радиус вписанной окружности в прямоугольный треугольник
выражается следующим образом: - Квадрат гипотенузы равен сумме квадратов катетов:
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Признаки равенства прямоугольных треугольников
С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.
- По двум катетам:
Если два катета одного прямоугольного треугольника соответственно
равны двум катетам другого прямоугольного треугольника,
то такие треугольники равны. - По катету и гипотенузе:
Если катет и гипотенуза одного прямоугольного треугольника соответственно
равны катету и гипотенузе другого прямоугольного треугольника,
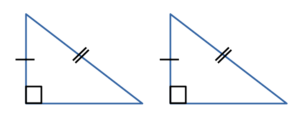
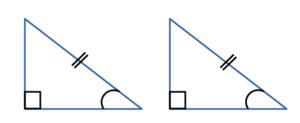
то такие треугольники равны. - По гипотенузе и острому углу:
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно
равны гипотенузе и острому углу другого прямоугольного треугольника,
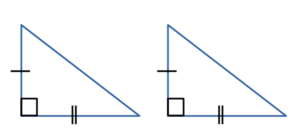
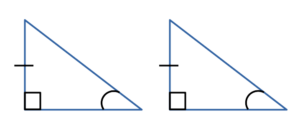
то такие треугольникиравны. - По катету и острому углу:
Если катет и острый угол одного прямоугольного треугольника соответственно
равны катету и острому углу другого прямоугольного треугольника,
то такие треугольники равны.
Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Признаки прямоугольного треугольника
С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.
- По теореме Пифагора:
Если квадрат стороны равен сумме квадратов двух других сторон,
то треугольник прямоугольный. - По центру описанной окружности:
Если центр описанной окружности лежит на стороне треугольника,
то треугольник прямоугольный. - По медиане:
Если медиана треугольника равна половине стороны, к которой она проведена,
то треугольник прямоугольный. - По площади:
Если площадь треугольника равна половине произведения двух его сторон,
то треугольник прямоугольный. - По радиусу описанной окружности:
Если радиус описанной окружности равен половине,
то треугольник прямоугольный.
Видео:36. Признаки равенства прямоугольных треугольниковСкачать

Признаки подобия прямоугольных треугольников
С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.
Видео:Геометрия 7 класс : Признаки равенства прямоугольных треугольниковСкачать

Признаки равенства прямоугольных треугольников с примерами решения
Содержание:
Признаки равенства прямоугольных треугольников:
Вы уже знаете три признака равенства треугольников. Поскольку часто приходится иметь дело с прямоугольными треугольниками, то выделяют пять признаков равенства прямоугольных треугольников. Сформулируем и докажем их.
Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

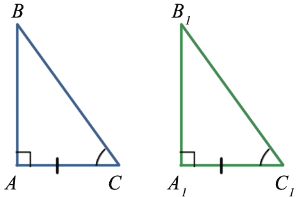
Второй признак (по катету и прилежащему острому углу)
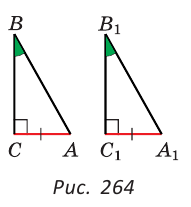
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано:
Доказать:
Доказательство:
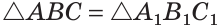
Видео:Признаки равенства треугольников. 7 класс.Скачать

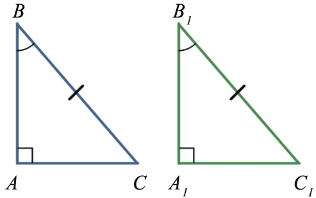
Третий признак (по катету и противолежащему острому углу)
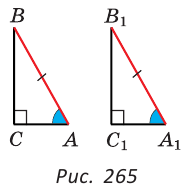
Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано: 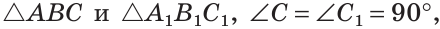
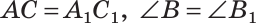
Доказать:
Доказательство:
Сумма острых углов прямоугольного треугольника равна 90°. Из того, что 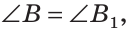
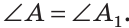
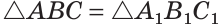
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

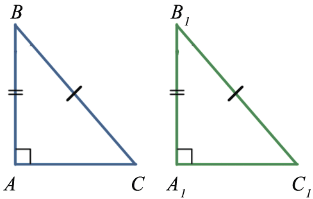
Четвертый признак (по гипотенузе и острому углу)
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано: 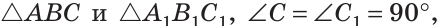
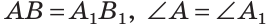
Доказать:
Доказательство:
Сумма острых углов прямоугольного треугольника равна 90°. Из того, что 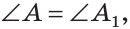
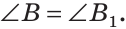
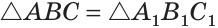
Видео:Признак равенства прямоугольных треугольников по катету и гипотенузеСкачать

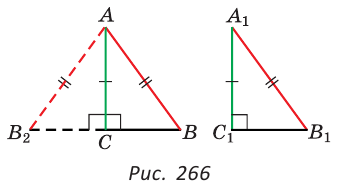
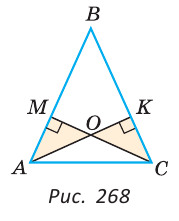
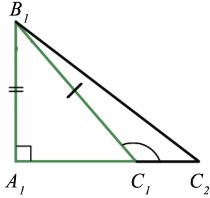
Пятый признак (по катету и гипотенузе).
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Дано: 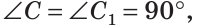
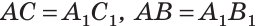
Доказать:
Доказательство:
Приложим треугольников А1В1С1 к треугольнику АВС так, чтобы совместились равные катеты А1С1 и АС, а вершины В1 и В лежали по разные стороны от прямой АС. Треугольник А1В1С1 займет положение треугольника АВ2С. Так как 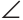
Отсюда
Пример:
На рисунке 267
Доказать равенство треугольников: а) 



Доказательство:
а) Рассмотрим прямоугольные треугольники ABC и ADC. У них гипотенуза АС — общая, катеты AD и ВС равны по условию. Тогда 

б) Из равенства треугольников ABC и ADC следует равенство сторон АВ и CD (доказано в пункте а). Тогда 

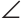
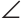
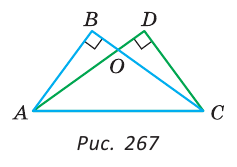
Пример:
Дан треугольник ABC, АК и СМ — его высоты, проведенные к боковым сторонам, О — точка их пересечения (рис. 268). Доказать, что если треугольники АОМ и СОК равны, то треугольник ABC — равнобедренный.
Доказательство:
Так как 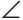
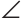
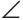
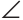
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Задачи на построение по геометрии
- Угол — определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Признаки равенства прямоугольных треугольников #11Скачать

Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников позволяют сравнивать прямоугольные треугольники лишь по двум элементам, так как любые два прямых угла равны.
1. Признак равенства по двум катетам
| Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны |
Данный признак следует из первого признака равенства треугольников.
Пример:


2. Признак равенства по катету и острому углу
| Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны |
Данный признак следует из второго признака равенства треугольников.
Пример:




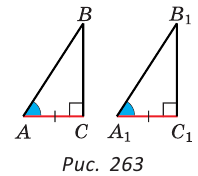
3. Признак равенства по гипотенузе и острому углу
Теорема
| Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого,то такие треугольники равны |
Пример:




Доказательство
Так как сумма двух острых углов прямоугольного треугольника равна 90 0 , то в таких треугольниках два других острых угла также равны, поэтому данные треугольники равны по второму признаку треугольников, т.е. по стороне(по гипотенузе) и двум прилежащим к ней углам, что и требовалось доказать.
4. Признак равенства по катету и гипотенузе
Теорема
| Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны |
Пример:


Доказательство
Дано: 

Доказать: 

Доказательство:
Рассмотрим данные треугольники:
Так как 



В 


Поделись с друзьями в социальных сетях:
📸 Видео
7 класс. Признаки равенства прямоугольных треугольников.Скачать

Равенство прямоугольных треугольников по гипотенузе и острому углуСкачать
Первые три признака равенства прямоугольных треугольниковСкачать

Доказательство I признака равенства прямоугольных треугольниковСкачать

ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

Геометрия 7 класс : Решение задач "Признаки равенства прямоугольных треугольников"Скачать

Прямоугольный треугольник. Признаки равенства прямоугольных треугольников - 7 класс геометрияСкачать

Признаки равенства прямоугольных треугольников. Видеоурок 18. Геометрия 7 класс.Скачать

Признаки равенства прямоугольных треугольников.Скачать