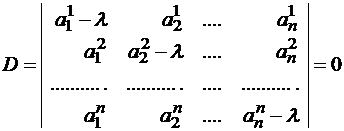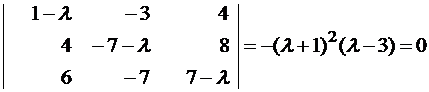Как доказать что вектор собственный (8 видео)

Собственные числа и собственные векторы линейного оператора

Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x ₁, x ₂, . x _m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x ₁, x ₂, . x _m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.
3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x ₁, x ₂, . x _n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 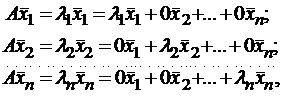тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе < ε _i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.

Содержание

Правило отыскания собственных чисел и собственных векторов
Свойства собственных векторов линейных операторов (преобразований)
Теорема (9.5) о разложении пространства в сумму корневых подпространств
Алгебраическая и геометрическая кратности собственных значений
Визуализация собственных значений и собственных векторов
Линейное преобразование
Собственные значения и собственные векторы
Алгебраическая и геометрическая кратность
Вывод
📹 Видео

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Правило отыскания собственных чисел и собственных векторов

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Пример №1 . Линейный оператор A действует в R₃ по закону A· x =(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, . x_n — координаты вектора x в базисе e ₁=(1,0,0), e ₂=(0,1,0), e ₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e ₁=(1,4,6)
A· e ₂=(-3,-7,-7)
A· e ₃=(4,8,7)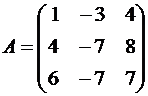
.
Составляем систему для определения координат собственных векторов:
(1-λ)x₁-3x₂+4x₃=0
x₁-(7+λ)x₂+8x₃=0
x₁-7x₂+(7-λ)x₃=0
Составляем характеристическое уравнение и решаем его:

Пример №2 . Дана матрица .
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор

Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i k =a_k i .

Замечания .

Все собственные числа симметрической матрицы вещественны.
Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Свойства собственных векторов линейных операторов (преобразований)

1. Собственные векторы линейного преобразования, принадлежащие различным собственным значениям, линейно независимы.

Аналогичное утверждение было доказано для собственных векторов матрицы (см. свойство 1).

2. Все собственные векторы линейного преобразования , принадлежащие одному собственному значению, совместно с нулевым вектором образуют линейное подпространство, инвариантное относительно преобразования . Такое линейное подпространство называется собственным для преобразования .

В самом деле, условие (9.5) можно записать в виде , где — тождественное преобразование. Множество векторов , удовлетворяющих последнему равенству, составляет ядро линейного преобразования , т.е. является линейным подпространством (собственное подпространство, отвечающее собственному значению ). Покажем, что это подпространство инвариантно относительно преобразования . Действительно, любой вектор в силу равенств отображается в коллинеарный ему вектор , также принадлежащий .

3. Для собственного значения линейного преобразования существует цепочка инвариантных подпространств

где ; — некоторое натуральное число .

Все перечисленные в цепочке (9.8) множества , являются линейными подпространствами по свойству ядра линейного преобразования. Каждое из подпространств инвариантно относительно преобразования , поскольку для любого вектора его образ , так как в силу перестановочности многочленов от одного и того же линейного преобразования (см. пункт 2 замечаний 9.3)

так как согласно определения ядра оператора.

Докажем включение . Если , то , при этом очевидно, что

Остальные включения доказываются аналогично.

Из цепочки (9.8) «расширяющихся» подпространств следует, что их размерности не убывают

поэтому в силу конечномерности пространства существует такое , что , т.е. . Покажем, что дальнейшего «увеличения» подпространств нет, т.е. для любого натурального . Предположим противное. Пусть и для некоторого 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQCAMAAACx1dbmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAiXFYMbEhAcBBoPDQoeAQ0I3cqgAAALZJREFUKM+VktsSwyAIRDWKiFf+/2uLSZvEhkxaXnTGs7KsGvN3UYrwC+ffa3D8zCMlxo+QlyfcNmg7v7A/t7VBux/jzkOe54lJURw8ZrHvop0UdM8P+3axGc89aqQ7XuxbjzybMkEUqPLAIPP6/u0g1OYUHnMpTQs02KLxq/0p0Y1O0al+RvqOCcv51CeZF1UeJBjhacoT6PJehTd9k/R7gdgPul7ei3itcWeYPp/sqv4fRhnzAuOaBpbDogV3AAAAAElFTkSuQmCC» /> пространства не совпадают: , то есть существует вектор , который не принадлежит пространству . Обозначим . Тогда, с одной стороны, , так как , поскольку . С другой стороны, , так как , поскольку . Следовательно, и и одновременно, что противоречит предположению .

Таким образом, в цепочке (9.8) размерности пространств , возрастают. Поэтому .

Корневым подпространством линейного преобразования для собственного значения называется линейное подпространство с наименьшим натуральным показателем , для которого .

4. Если — собственное значение линейного преобразования , то пространство можно представить в виде прямой суммы , где — корневое подпространство, а — инвариантное относительно подпространство, в котором нет собственных векторов, принадлежащих собственному значению .

В самом деле, покажем, что пересечение этих подпространств есть нулевой вектор: . Выберем вектор . Так как вектор , то существует такой вектор , что . Поскольку , то . Тогда . Следовательно, вектор , но , так как — корневое подпространство. Значит,

По теореме 9.1 о размерности ядра и образа получаем, что . Следовательно, пространство можно представить в виде прямой суммы подпространств (см. признаки прямых сумм подпространств).

Докажем, что в нет собственных векторов, принадлежащих собственному значению . Действительно, пусть — собственный вектор, соответствующий собственному значению . Тогда и в силу (9.8) . Подпространство имеет с только один общий вектор (нулевой). Поэтому , так как . Инвариантность подпространства следует из перестановочности операторов и (см. пункт 2 замечаний 9.3). В самом деле, для любого вектора существует прообраз . Поэтому в силу перестановочности операторов

поскольку и . Таким образом, инвариантность подпространства доказана, так как .

Видео:Собственные векторы и собственные значения матрицыСкачать

Теорема (9.5) о разложении пространства в сумму корневых подпространств

Если все различные корни характеристического уравнения линейного преобразования являются его собственными значениями, то пространство можно разложить в прямую сумму инвариантных (корневых) подпространств:

где — корневое подпространство, соответствующее собственному значению .

В самом деле, по свойству 4 можно «отщепить» корневое подпространство , т.е. представить пространство в виде прямой суммы инвариантных подпространств , причем в нет собственных векторов, принадлежащих собственному значению . В пространстве определено сужение преобразования . Применяя свойство 4 к сужению , аналогичным образом можно «отщепить» корневое подпространство , т.е. представить пространство в виде прямой суммы инвариантных подпространств: . Этот процесс следует продолжить до тех пор, пока не исчерпаются все корни характеристического уравнения.

Следствие. Если все различные корни характеристического уравнения линейного преобразования являются его собственными значениями, то существует базис пространства , в котором матрица линейного преобразования имеет блочно-диагональный вид

где — матрицы сужений , преобразования на корневые подпространства.

Согласно следствию из теоремы 9.2, такой базис можно получить, записывая последовательно базисы корневых подпространств (9.9).

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Алгебраическая и геометрическая кратности собственных значений

Алгебраической кратностью собственного значения линейного оператора (преобразования) называется кратность корня характеристического многочлена (или, что то же самое, кратность корня характеристического уравнения ).

Геометрической кратностью собственного значения линейного оператора (преобразования) называется размерность собственного подпространства , соответствующего этому собственному значению.

Теорема 9.6 о кратностях собственных значений оператора. Геометрическая кратность собственного значения не превосходит его алгебраической кратности.

Представим пространство в виде прямой суммы (см. свойство 4) и обозначим . Выбрав базис пространства , дополним его до базиса всего пространства. В этом базисе, согласно следствию теоремы 9.5, матрица преобразования будет иметь блочно-диагональный вид , где квадратная матрица порядка является матрицей сужения преобразования на подпространство , а матрица является матрицей сужения . Характеристический многочлен матрицы имеет вид (см. определитель блочно-диагональной матрицы)

где — многочлены степеней и соответственно. Так как сужение не имеет собственных значений, отличных от , то , в силу того, что и основной теоремы алгебры. Поскольку сужение не имеет собственных векторов, принадлежащих собственному значению , то . Следовательно, -алгебраическая кратность собственного значения . Тогда утверждение теоремы следует из включения (9.8): , так как .

Видео:Как разложить вектор по базису - bezbotvyСкачать

Визуализация собственных значений и собственных векторов

Дата публикации Aug 24, 2019

Собственные значения и собственные векторы являются очень важной концепцией в линейной алгебре и машинном обучении в целом. В моем предыдущемстатьяЯ представлял эти концепции с точки зрения анализа основных компонентов, предоставляя практические примеры. В этой статье я подробнее остановлюсь на математике, лежащей в основе этих понятий, и предоставлю геометрическую интерпретацию того, что собираюсь объяснить.

Для этого я расскажу о следующей теме:

Линейное преобразование
Собственные значения и собственные векторы
Алгебраическая и геометрическая кратность

Итак, начнем с первой темы.

Видео:Коллинеарность векторовСкачать

Линейное преобразование

Вообще говоря, преобразование — это любая функция, определенная в доменном пространстве V с выходами в кодомене W (где V и W — многомерные пространства, не обязательно евклидовы).

Преобразование, которое сохраняет операции сложения и скалярного умножения следующим образом:

Называется Linear Transformation, и теперь мы будем называть его T.

Давайте рассмотрим следующие два числовых примера, чтобы иметь это в виду. Представьте, что мы получили преобразование T, определенное в R2, с выходами в R:

Как видите, это преобразование не является линейным, поскольку не сохраняет аддитивности. А как насчет этого?

Как видите, аддитивность и умножение на скаляр сохраняются, следовательно, преобразование является линейным. Стоит отметить, что единственными линейными преобразованиями из R2 в R являются те, которые выглядят как w = ax + by, следовательно, линейные комбинации компонентов векторов области.

Очень важное свойство линейных систем задается теоремой о представлении, которая утверждает, что линейное преобразование может быть представлено следующим образом:

Где A — это так называемая матрица представления. Мы будем использовать эту формулу, поскольку она более компактна и удобна.

Теперь каждое преобразование может влиять на направление и расширение вектора (для более ясного объяснения формы векторов в многомерном пространстве вы можете прочитать мою предыдущую статьюВот). Однако, учитывая преобразование T, существует очень интересный класс векторов, на которые это преобразование влияет только с точки зрения расширения, поскольку направление остается неизменным. Общий векторvс этим свойством таково, что:

гделямбдаявляется фактором расширения. Эти векторы называются собственными векторами, а значениелямбдасвязанный с ними называется собственное значение.

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Собственные значения и собственные векторы

Как и предполагалось, собственными векторами являются те векторы, направление которых остается неизменным после преобразования через фиксированный T, а собственными значениями являются те значения коэффициента расширения, которые связаны с ними.

Чтобы быть более точным, собственные векторы являются векторами, которые не являются тривиальными, следовательно, отличаются от0, Это потому, что равенство выше всегда имеет по крайней мере одно решение, которое является тривиальнымv = 0,

Как мы можем найти наши собственные векторы и собственные значения при условии, что эти первые отличаются от тривиального вектора? Для этого давайте переосмыслим нашу линейную систему с помощью теоремы о представлении:

Как и ожидалось, эта система имеет по крайней мере одно решение, которое является тривиальным. Следовательно, мы хотим найти те значения лямбды, для которых определитель матрицы (A-лямда* I) равно нулю (в противном случае это означало бы, что из-за теоремы Крамера система имеет 1 единственное решение).

Итак, давайте установим наше уравнение:

Это уравнение называется характеристическим уравнением, а его корнями являются собственные значения. Кроме того, из-за основной теоремы алгебры«Каждый многочлен степени n имеет n решений в C (множество комплексных чисел)»мы знаем, что степень характеристического уравнения будет числом собственных значений, связанных с этой системой.

Давайте рассмотрим следующий пример:

Из характеристического уравнения мы вывели два собственных значения 3 и -1. Чтобы привести числовой пример, я собираюсь найти векторы, называемые собственными векторами, связанными слямбда= 3 (то же самое верно длялямбда= -1). Быстрый ярлык для этой цели может быть полезен, если мы рассмотрим матрицу A. Действительно, поскольку мы просили неединственность решения, мы уже знаем, что определитель матрицы (A-lI) равен 0, следовательно, пока Решив получившуюся систему, мы можем напрямую избавиться от одного из двух ограничений:

Давайте визуализируем это:

По сути, все векторы, которые лежат на этой прямой линии, являются собственными векторами, связанными с собственным значением 3: после преобразования через T они будут только расширяться / сокращаться, но не изменяться в направлении. Рассмотрим, например, следующий вектор:

Теперь давайте изменим это:

Как видите, его величина теперь в 3 раза больше, но направление остается прежним

Теперь давайте перейдем к последней теме этой статьи — алгебраической и геометрической множественности, связанной с собственными значениями и собственными векторами.

Видео:Образуют ли данные векторы базисСкачать

Алгебраическая и геометрическая кратность

Теперь представьте, что у вас есть характерное уравнение степениNно вы найдете только один корень. Следовательно, поскольку степеньNэтот корень, как говорят, имеет алгебраическую кратностьN, Давайте рассмотрим два следующих примера:

В первом случае мы имеем одно собственное значение, равное -2, не имеет кратности (поскольку его мощность равна 1), в то время как собственное значение -1 (из многочлена 2-й степени) будет иметь кратность, равную 2.

Теперь вопрос: уважается ли эта множественность и с геометрической стороны проблемы? Другими словами, равняется ли количество раз, когда собственное значение появляется в решении, равному размерам / степеням свободы соответствующего собственного пространства (которое является набором связанных собственных векторов)?

Ответ не всегда. Всякий раз, когда у нас есть собственное значение с кратностью, равнойNи соответствующее собственное пространство с размерами меньшеNмы называем этот коэффициент лямбда нерегулярным (в противном случае собственные значения называются регулярными).

Давайте наглядно представим это на примере выше:

Как видите, даже если у нас есть собственное значение с кратностью 2, ассоциированное собственное пространство имеет только одно измерение, так как оно равно y = 0.

Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Вывод

Собственные значения и собственные векторы являются фундаментальными в науке о данных и построении модели в целом. Помимо их использования в PCA, они используются, в частности, в спектральной кластеризации и сжатии изображений. Следовательно, важно иметь в виду их геометрическую интерпретацию.