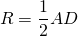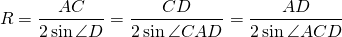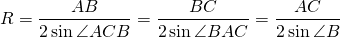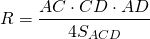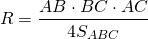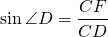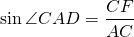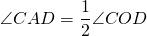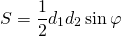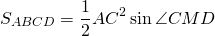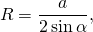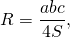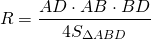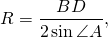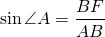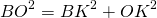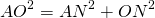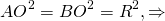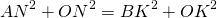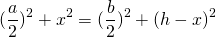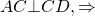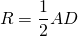Знание — сила. Познавательная информация
Видео:ОГЭ ЗАДАНИЕ 16 РАДИУС ОКРУЖНОСТИ ВПИСАННОЙ В ТРАПЕЦИЮ РАВЕН 18. НАЙДИТЕ ВЫСОТУ ЭТОЙ ТРАПЕЦИИСкачать
Трапеция вписана в окружность
Рассмотрим несколько направлений решения задач, в которых трапеция вписана в окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
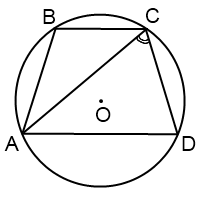
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
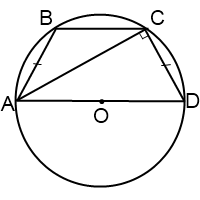
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции лежит внутри трапеции.
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
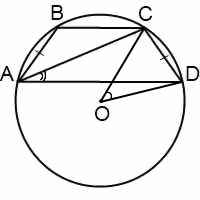
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,
Кстати, использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
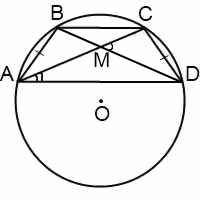
В равнобедренном треугольнике AMD углы при основании равны. Внешний угол CMD равен сумме внутренних углов, не смежных с ним:
Видео:Радиус описанной окружности трапецииСкачать
Задание №1207
Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать
Условие
В окружность вписана трапеция ABCD с основаниями AD и BC , один из углов которой равен 60^. В трапецию вписана ещё одна окружность.
а) Докажите, что центр описанной окружности трапеции лежит внутри трапеции.
б) Найдите, во сколько раз CD больше радиуса окружности, касающейся сторон AB , AD и вписанной окружности трапеции ABCD , если AD>BC.
Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать
Решение
а) План решения.
1 . Сделаем чертёж, считая для определённости, что AD>BC (для пункта а) это не имеет значения).
2 . Заметим, что трапеция равнобедренная. Обозначим одну из сторон трапеции какой-либо буквой, выразим остальные стороны.
3 . Выразим через ту же букву радиус окружности, описанной около трапеции: это можно сделать по теореме синусов для triangle ABD.
4 . Обозначим точкой N середину AD , точкой M — середину BC . Найдём CN .
5 . Сравним CN с радиусом описанной окружности. Сделаем вывод, учитывая, что радиус описанной окружности лежит на прямой MN .
1 . Выполним чертёж.
2 . Так как трапеция ABCD вписана в окружность, то она равнобедренная, то есть AB=CD=a. angle BAD=60^. Следовательно, AH =frac12 AB=frac12 a, KD=frac12 a. a. Так как в ABCD вписана окружность, то AB+CD=BC+AD, отсюда BC =frac12 a и AD=frac32 a.
3 . Радиус описанной окружности трапеции ABCD равен радиусу описанной окружности triangle ABD. Из triangle ABD по теореме синусов 2R= frac = frac2cdot sqrt = frac2cdot sqrt <left( frac2 right) ^2+a^2>= frac a, R=frac a.
4 . Центр O описанной окружности трапеции ABCD лежит на прямой MN , где M и N — середины BC и AD соответственно. CN= sqrt = sqrt <left( frac2 right)^2+left(frac a4 right)^2>= frac<sqrt >4 a.
5 . Сравним CN и R, frac<sqrt >4>frac то есть sqrt >sqrt , отсюда MN>OM или радиус описанной окружности лежит на прямой MN , а центр описанной окружности лежит внутри отрезка MN .
б) План решения.
1 . Сделаем чертёж, обозначив центр вписанной окружности через O_1, а центр второй окружности — через O_2. Построим радиус O_2T perp AD.
2 . Из подобных треугольников O_2AT и O_1AN, зная angle O_2AT, вычислим O_2T.
3 . Найдём искомое отношение frac.
1 . Выполним чертёж.
2. triangle O_2AT sim triangle O_1AN, тогда frac=frac. Обозначим искомый радиус O_2T через x , получим: fracx= frac. BH=MN, из triangle ABH: BH=ABcdot sin 60^=frac2 , MN =frac2.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, поэтому angle O_1AN =frac12 angle BAD=30^. Тогда AO_1=2O_1N (катет, лежащий против угла в 30^, равен половине гипотенузы). Отсюда fracx=frac , frac1x =frac2 , O_1N-x=2x, x= frac13 O_1N= frac13cdot frac12 MN= frac16cdot frac 2= frac , x=frac , то есть O_2T=frac.
Видео:Трапеция и вписанная окружностьСкачать
Радиус описанной окружности трапеции
Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул
где a — сторона треугольника, α — противолежащий ей угол;
либо по формуле
где a, b, c — стороны, S — площадь треугольника.
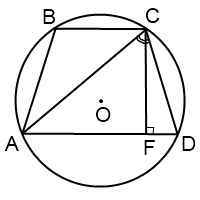
Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
где синус угла A можно найти из прямоугольного треугольника ABF:
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
и приравнять правые части
Решив это уравнения относительно x, можно найти R.
IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.
точка O — середина AD
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.
I вариант нахождения радиуса для этого случая не изменяется.
Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.
Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.
💡 Видео
Задача про трапецию, описанную около окружностиСкачать
Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать
Малоизвестные свойства равнобедренной трапеции. Разбор задачи 17 ЕГЭ профиль.Скачать
ОГЭ Задание 24 Вписанная трапецияСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать
✓ Как решить трапецию | ЕГЭ-2020. Задание 16. Профильный уровень. Основная волна | Борис ТрушинСкачать
Геометрия Центр окружности, описанной около равнобокой трапеции, принадлежит ее большему основаниюСкачать
ОГЭ Задача 26 Окружность в трапецииСкачать
Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать
Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
Где лежит центр описанной окружности? 1 задание ЕГЭ ПрофильСкачать
