Основные свойства треугольника огэ (4 видео)

Необходимый теоретический материал для успешной сдачи ОГЭ-9 по математике для учеников разной подготовленности

Класс: 9

Ключевые слова: математика , ОГЭ

Содержание

1. Углы
2. Медиана, биссектриса, высота
3. Треугольник
3. Четырехугольники
4. Окружность
Подготовка к ОГЭ по теме: «Треугольники»
Геометрия. Урок 3. Треугольники
Определение треугольника
Виды треугольников
Отрезки в треугольнике
Площадь треугольника
Равнобедренный треугольник
Равносторонний треугольник
Прямоугольный треугольник
Теорема Пифагора
Примеры решений заданий из ОГЭ
📽️ Видео

1. Углы

Вертикальные углы равны (на рис. 1 и 3; 6 и 8 и др.).

Внутренние накрест лежащие углы при параллельных прямых и секущей равны. (на рис. 4 и 6; 1 и 7).

Сумма внутренних односторонних углов при параллельных прямых и секущей равна 180˚ (на рис. 4 и 7; 1 и 6).

Соответственные углы при параллельных прямых и секущей равны. (на рис. 3 и 7; 1 и 5 и др.).

Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.

2. Медиана, биссектриса, высота

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

Высота треугольника – перпендикуляр опущенный из вершины угла на противоположную сторону.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

В любом треугольники все биссектрисы пересекаются в одной точке, все медианы пересекаются в одной точке, все медианы пересекаются в одной точке.

3. Треугольник

Сумма углов в любом треугольнике 180˚.

Средняя линия треугольника – прямая проходящая через середины двух сторон. Средняя линия параллельна одной из сторон и равна половине этой стороны.

Виды треугольников: тупоугольный (один угол тупой), прямоугольный (один угол прямой 90˚), остроугольный (все углы острые, меньше 90˚).

Равнобедренный треугольник — треугольник, у которого равны две стороны.

Свойства равнобедренного треугольника:

в равнобедренном треугольнике углы при основании равны;
в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

Равносторонний треугольник — треугольник, у которого все стороны равны. (все углы по 60 градусов)

Всякий равносторонний треугольник является равнобедренным, но не всякий равнобедренный — равносторонним.

Три признака равенства треугольников

I признак по двум сторонам и углу между ними

II признак (по стороне и прилежащим углам)

III признак (по трем сторонам)

Признаки подобия треугольников

I признак по двум равным углам

II признак по двум пропорциональным сторонам и углу между ними

III признак по трем пропорциональным сторонам

Площади подобных фигур относятся как коэффициент подобия в квадрате.

Объемы подобных фигур относятся как коэффициент подобия в кубе.

Треугольник называется прямоугольным, если один из его углов прямой.

Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой. (самая большая сторона это гипотенуза, две др катеты).

Свойства прямоугольного треугольника

Сумма острых углов прямоугольного треугольника равна 90 градусов.

Катет, лежащий против угла в 30˚, равен половине гипотенузы.

Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.

Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: a² + b² = c².

Пифагоровы тройки:

Признаки равенства прямоугольных треугольников

По двум катетам.
По гипотенузе и катету.
По катету и прилежащему острому углу.
По катету и противолежащему острому углу.
По гипотенузе и острому углу.

Признаки подобия прямоугольных треугольников:

По острому углу.
По пропорциональности двух катетов.
По пропорциональности катета и гипотенузы.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному.

Высота прямоугольного треугольника: h=ab/c или h = (где АВ гипотенуза, СЕ высота опущенная на гипотенузу).

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы: m=c/2 (R=с/2=mc).

3. Четырехугольники

Сумма углов в любом четырехугольнике 360˚.

Параллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны.

У параллелограмма противолежащие стороны равны и противолежащие углы равны.

Сумма любых двух соседних углов параллелограмма равна 180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Каждая диагональ делит параллелограмм на два равных треугольника.

Две диагонали параллелограмма делят его на четыре равновеликих треугольника.

Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

Ромбом называется параллелограмм, у которого все стороны равны.

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые.

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка.

Квадрат.

Квадрат – это прямоугольник, у которого все стороны равны.

Диагонали квадрата равны и перпендикулярны.

Сторона и диагональ квадрата связаны соотношениями: .

Трапеция

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны.

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.

Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Равнобокой называется трапеция, у которой боковые стороны равны.

У равнобокой трапеции: диагонали равны; углы при основании равны; сумма противолежащих углов равна 180.

Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c².

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

4. Окружность

Отрезок, соединяющий центр окружности с любой точкой окружности называется радиусом (r) окружности.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности.

Прямая, имеющая с окружностью одну общую точку, называется касательной. Касательная и радиус проведенный в точку касания пересекаются под прямым углом.

Прямая, имеющая с окружностью две общие точки, называется секущей.

Центральный угол окружности – это угол, вершина которого лежит в центре окружности. Центральный угол равен дуге на которую он опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее. Вписанный угол равен половине дуги на которую опирается.

Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

Вписанный угол, опирающийся на диаметр равен 90˚.

Все вписанные углы, опирающиеся на одну и туже дугу равны.

Теорема косинусов:

Теорема синусов:

5. Формулы площадей

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Подготовка к ОГЭ по теме: «Треугольники»

Составители: учителя математики МОУ «Рамешковская СОШ» , .

Пояснительная записка: геометрическая часть экзаменационного теста чаще всего вызывает затруднение. Это происходит потому что геометрические задачи требуют иного подхода, чем любые другие. Тут необходимо применить нестандартное мышление и пространственное воображение, кроме того необходимо очень хорошо знать теоретический материал. Решение каждой задачи опирается на какое-либо правило, теорему или определение. Поэтому прежде всего нужно выучить теорию. В данном материале подобраны теория и задачи к ней.

Цель: 1. Систематизация знаний и способов деятельности обучающихся по математике по данному разделу за курс основной школы;

2. Подготовка обучающихся 9 класса к ОГЭ;

3. Успешное сдача ОГЭ.

Задачи: 1. Осуществить информационное, методическое обеспечение итоговой аттестации выпускников 9 классов;

2. Формирование «базы знаний» по геометрии, позволяющей беспрепятственно оперировать математическим материалом;

3. Формирование навыков определения типа задачи и оптимального способа ее решения;

4. Умение работать с геометрическими задачами.

Выбрать верные утверждения:

а) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

б) Если сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны.

в)Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Два острых угла прямоугольного треугольника относятся как 11:79. Найдите больший острый угол. Ответ дайте в градусах. Один из острых углов прямоугольного треугольника равен 26◦. Найдите другой острый угол. Ответ дайте в градусах. Два острых угла прямоугольного треугольника относятся как 2:8. Найдите меньший острый угол. Ответ дайте в градусах. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.

В треугольнике ABC AC = BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.

Один из острых углов прямоугольного треугольника равен 23◦. Найдите его другой острый угол. Ответ дайте в градусах. В треугольнике два угла равны 27◦ и 79◦. Найдите его третий угол. Ответ дайте в градусах. В треугольнике ABC известно, что AB=BC, ∠ABC = 146◦. Найдите ∠BCA. Ответ дайте в градусах. Какие из следующих утверждений верны:

а) Если угол острый, то смежный с ним угол также является острым.

б) Всегда один из двух смежных углов острый, а другой тупой.

в) Сумма углов треугольника равна 180◦.

г) Треугольника со сторонами 1, 2, 4 не существует.

д) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны.

е) Сумма острых углов прямоугольного треугольника равна 90◦ .

ж) Смежные углы равны.

з) Один из углов треугольника всегда не превышает 60 градусов.

и) Если три угла одного треугольника равны соответственно трем углам другого треугольника, то такие треугольник равны.

к) В тупоугольном треугольнике все углы тупые.

4. В треугольнике АВС стороны АС и ВС равны. Внешний угол при вершине В равен 116°. Найдите угол С. Ответ дайте в градусах.

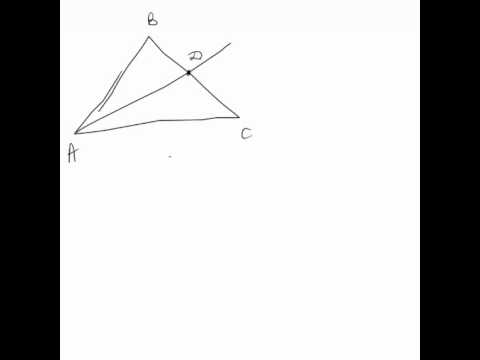
Точка D на стороне АВ треугольника АВС выбрана так, что АD=АС. Известно, что ∠CАВ = 25◦. И ∠АСВ = 146◦. . Найдите ∠DCB. Ответ дайте в градусах.

В треугольнике АВС известно, что АС=ВС. Внешний угол при вершине В равен 107◦. Найдите угол С. Ответ дайте в градусах.

В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите ∠МРN.

В треугольнике ABC известно, что ∠BCA= 60◦, AD биссектриса. Найдите ∠BAD. Ответ дайте в градусах. В треугольнике ABC известно, что AC= 58, BM-медианна, BM=37. Найдите AM. На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённую из вершины прямого угла.

В равностороннем треугольнике ABС биссектрисы СN и AM пересекаются в точке P. Найдите ∠МРN.

В треугольнике АВС известно, что АВ=ВС=25, АС=40. Найдите длину медианы ВМ. В треугольнике со сторонами 12 и 3 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 1. Чему равна высота, проведенная ко второй стороне?

Медиана ВМ и биссектриса АР треугольника АВС пересекаются в точке К, длина стороны АС относится к длине стороны АВ как 9:4. Найдите отношение площади треугольника АВК к площади четырехугольника КРСМ. В треугольнике АВС на его медиане ВМ отмечена точка К так, что ВК:КМ=2:11. Прямая АК пересекает сторону ВС в точке Р. Найдите отношение площади треугольника ВКР и площади треугольника АКМ. Медиана ВМ и биссектриса АР треугольника АВС пересекаются в точке К, длина стороны АС относится к длине стороны АВ как 11:6. Найдите отношение площади треугольника ВКР к площади треугольника АВК. Прямая параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках К и М соответственно. Найдите АС, если ВК:КА=2:3, КМ=4. Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?

На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?

Два катета прямоугольного треугольника равны 3 и 22. Найдите его площадь. Медиана равностороннего треугольника равна 12√3. Найдите его сторону. Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника. Стороны треугольника равны 12, 14 и 10. Найдите го площадь. Сторона треугольника равна 24, а высота, проведенная к этой стороне равна 19. Найдите площадь этого треугольника. В прямоугольном треугольнике катет и гипотенуза равны соответственно 12 и 20. Найдите другой катет этого треугольника. Бокова сторона равнобедренного треугольника равна 10, основание 12. Найдите его площадь. Найдите площадь равностороннего треугольника если его сторона равна 8. Стороны треугольна равны 10 и 6, угол между ними 30◦. Найдите его площадь. Сторона равностороннего треугольника равна 12√3. Найдите его биссектрису. В прямоугольном треугольнике меньший катет равен 6, а один из углов 30◦. Найдите площадь треугольника. Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18. Стороны треугольника равны 16 и 9, угол между ними 60◦. Найдите его площадь. Высота треугольника, проведенная к гипотенузе делит ее на отрезки, равны 4 и 9. Найдите площадь треугольника. Гипотенуза равнобедренного треугольника равна 16. Найдите го площадь. Площадь треугольника равна 270 , сторона 5. Найдите высоту, проведенную к данной стороне. Один из катетов равен 12, другой составляет 0,6 первого. Найдите площадь этого треугольника. Гипотенуза треугольника равна 5, один из катетов равен 3. Найдите площадь этого треугольника. Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.

Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 48, а площадь равна 288. Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√2. Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 36, а площадь равна 162√3. Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?

Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?

Соотношения между сторонами и углами прямоугольного треугольника

В треугольнике ABC угол С равен 90◦, АС=4, cosA=0,5. Найдите АВ.

Найдите тангенс угла А треугольника ABC, изображённого на рисунке.

В прямоугольном треугольнике ∠С=90◦, tgА=3,5. Найти АС, если ВС=2,8. В равнобедренном треугольнике АВС ВС=СА=15. Чему равна высота, опущенная на АВ, если sinA=0,9. Найдите tgA треугольника ABC, изображенного на рисунке.

Катеты прямоугольного треугольника равны √15 и 1. Найдите синус наименьшего угла этого треугольника.

В треугольнике АВС средняя линия MN параллельна стороне AC. Найдите периметр треугольника ABC, если периметр треугольника MBN равен 17 см. В треугольнике АВС DE – средняя линия. Площадь треугольника CDE равна 20. Найдите площадь треугольника АВС.

Периметр равностороннего треугольника АВС равен 24 см. Найдите длину средней линии этого треугольника. Точки M и N являются серединами сторон АВ и ВС треугольника АВС, АС=22. Найдите MN. Точки D и K являются серединами сторон АВ и ВС треугольника АВС, АС=88. Найдите DK. В треугольнике АВС известно, что DE – средняя линия. Площадь треугольника CDE равна 8. Найдите площадь треугольника АВС.

В треугольнике АВС отмечены середины М и N сторон ВС и АС соответственно. Площадь треугольника CNМ равна 38. Найдите площадь четырехугольника ABMN.

В треугольнике АВС АС = 35, ВС=5√15 угол С равен 90°. Найдите радиус описанной окружности этого треугольника. Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?

Сторона AC треугольника ABC содержит центр описанной около него окружности. Найдите ∠С, если ∠А=75◦. Ответ дайте в градусах.

В треугольнике АВС известны длины сторон АВ=48, АС=72, точка О – центр окружности, описанной около треугольника АВС. Прямая ВD, перпендикулярная прямой АО, пересекает сторону АС в точке D. Найдите СD. Углы В и С треугольника АВС равны соответственно 71◦ и 79◦. Найдите ВС, если радиус окружности, описанной около треугольника АВС, равен 8. В треугольнике АВС известно, что АС=15, ВС= 5√7, угол С равен 80◦. Найдите радиус описанной окружности этого треугольника. Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Видео:Свойства равнобедренного треугольника #огэ #математика #shortsСкачать

Геометрия. Урок 3. Треугольники

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение треугольника

Виды треугольников

Отрезки в треугольнике

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Определение треугольника

Треугольник – многоугольник с тремя сторонами и тремя углами.

Угол ∠ A – угол, образованный сторонами A B и A C и противолежащий стороне B C .

Угол ∠ B – угол, образованный сторонами B A и B C и противолежащий стороне A C .

Угол ∠ C – угол, образованный сторонами C B и C A и противолежащий стороне A B .

Видео:Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

Виды треугольников

Треугольник остроугольный , если все три угла в треугольнике острые.

Треугольник прямоугольный , если у него один из углов прямой ( = 90 ° ) .

Треугольник тупоугольный , если у него один из углов тупой.

Основные свойства треугольника:

Против большей стороны лежит больший угол.
Против равных сторон лежат равные углы.
Сумма углов в треугольнике равна 180 ° .
Если продолжить одну из сторон треугольника, например, A C , и взять на продолжении стороны точку D , образуется внешний угол ∠ B C D к исходному углу ∠ A C B .

Видео:Вся геометрия 7–9 класс с нуля | ОГЭ МАТЕМАТИКА 2023Скачать

Отрезки в треугольнике

Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.

Свойства биссектрис треугольника:

Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:

Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Свойства медиан треугольника:

Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.

Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.

Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.

Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.

Видео:ВЫСОТА ТРЕУГОЛЬНИКА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Площадь треугольника

Площадь произвольного треугольника можно найти следующими способами:

Видео:ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

Равнобедренный треугольник

Равнобедренным называется треугольник, у которого две стороны равны.

Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.

Свойства равноберенного треугольника:

В равнобедренном треугольнике углы при основании равны.
В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию, совпадают.

Видео:ЕГЭ 2024. ВСЁ ПРО ТРЕУГОЛЬНИКИ за 15 минутСкачать