Как доказать что центр окружности делит диаметр пополам

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Диаметр делит хорду пополам

Если диаметр делит хорду пополам, каково их взаимное расположение?

Если диаметр делит хорду пополам, то он перпендикулярен этой хорде.

Дано: окружность (O;R),

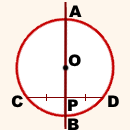
AB — диаметр, CD — хорда,

Соединим концы хорды CD с точкой O — центром окружности.

Так как OC=OD (как радиусы), то треугольник COD — равнобедренный с основанием CD.

Так как CP=PD, то OP — медиана треугольника COD, проведённая к основанию.

По свойству равнобедренного треугольника, OP является также его высотой.

Как доказать что центр окружности делит диаметр пополам

§ 20. Некоторые свойства окружности. Касательная к окружности

Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.

Если хорда является диаметром, то теорема очевидна.

На рисунке 287 изображена окружность с центром O , M — точка пересечения диаметра CD и хорды AB , CD ⊥ AB . Надо доказать, что AM = MB .

Проведём радиусы OA и OB . В равнобедренном треугольнике AOB ( OA = OB ) отрезок OM — высота, а значит, и медиана, т. е. AM = MB .

Диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.

Докажите эту теорему самостоятельно. Подумайте, будет ли верным это утверждение, если хорда является диаметром.

На рисунке 288 показаны все возможные случаи взаимного расположения прямой и окружности. На рисунке 288, а они не имеют общих точек, на рисунке 288, б — имеют две общие точки, на рисунке 288, в — одну.

Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.

Касательная к окружности имеет только одну общую точку с кругом, ограниченным этой окружностью. На рисунке 288, в прямая a — касательная к кругу с центром в точке O , A — точка касания.

Если отрезок (луч) принадлежит касательной к окружности и имеет с этой окружностью общую точку, то говорят, что отрезок (луч) касается окружности. Например, на рисунке 289 изображён отрезок AB , который касается окружности в точке С .

Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

На рисунке 290 изображена окружность с центром O , A — точка касания прямой a и окружности. Надо доказать, что OA ⊥ a .

Предположим, что это не так, т. е. отрезок OA — наклонная к прямой a . Тогда из точки O опустим перпендикуляр OM на прямую a (рис. 291). Поскольку точка A — единственная общая точка прямой a и круга с центром O , то точка M не принадлежит этому кругу. Отсюда OM = MB + OB , где точка B — точка пересечения окружности и перпендикуляра OM . Отрезки OA и OB равны как радиусы окружности. Таким образом, OM > OA. Получили противоречие: перпендикуляр OM больше наклонной OA . Следовательно, OA ⊥ a .

(признак касательной к окружности)

Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведённому в эту точку, то эта прямая является касательной к данной окружности.

На рисунке 290 изображена окружность с центром в точке O , отрезок OA — её радиус, точка A принадлежит прямой a , OA ⊥ a . Докажем, что прямая a — касательная к окружности.

Пусть прямая a не является касательной, а имеет ещё одну общую точку B с окружностью (рис. 292). Тогда ∆ AOB — равнобедренный ( OA = OB как радиусы). Отсюда ∠ OBA = ∠ OAB = 90°. Получаем противоречие: в треугольнике AOB есть два прямых угла. Следовательно, прямая a является касательной к окружности.

Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.

Докажите это следствие самостоятельно.

Задача. Докажите, что если через данную точку к окружности проведены две касательные, то отрезки касательных, соединяющих данную точку с точками касания, равны.

Решение. На рисунке 293 изображена окружность с центром O . Прямые AB и AC — касательные, точки B и C — точки касания. Надо доказать, что AB = AC .

Проведём радиусы OB и OC в точки касания. По свойству касательной OB ⊥ AB и OC ⊥ AC . В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC .

507. Начертите окружность с центром O , проведите хорду AB . Пользуясь угольником, разделите эту хорду пополам.

508. Начертите окружность с центром O , проведите хорду CD . Пользуясь линейкой со шкалой, проведите диаметр, перпендикулярный хорде CD .

509. Начертите окружность, отметьте на ней точки A и B . Пользуясь линейкой и угольником, проведите прямые, которые касаются окружности в точках A и B .

510. Проведите прямую a и отметьте на ней точку M . Пользуясь угольником, линейкой и циркулем, проведите окружность радиуса 3 см, которая касается прямой a в точке M . Сколько таких окружностей можно провести?

511. На рисунке 294 точка O — центр окружности, диаметр CD перпендикулярен хорде AB . Докажите, что ∠ AOD = ∠ BOD .

512. Докажите, что равные хорды окружности равноудалены от её центра.

513. Докажите, что если хорды окружности равноудалены от её центра, то они равны.

514. Верно ли, что прямая, перпендикулярная радиусу окружности, касается этой окружности?

515. Прямая CD касается окружности с центром O в точке A , отрезок AB — хорда окружности, ∠ BAD = 35° (рис. 295). Найдите ∠ AOB .

516. Прямая CD касается окружности с центром O в точке A , отрезок AB — хорда окружности, ∠ AOB = 80° (см. рис. 295). Найдите ∠ BAC .

517. Дана окружность, диаметр которой равен 6 см. Прямая a удалена от её центра на: 1) 2 см; 2) 3 см; 3) 6 см. В каком случае прямая a является касательной к окружности?

518. В треугольнике ABC известно, что ∠ C = 90°. Докажите, что:

1) прямая BC является касательной к окружности с центром A , проходящей через точку C ;

2) прямая AB не является касательной к окружности с центром C , проходящей через точку A .

519. Докажите, что диаметр окружности больше любой хорды, отличной от диаметра.

520. В окружности с центром O через середину радиуса провели хорду AB , перпендикулярную ему. Докажите, что ∠ AOB = 120°.

521. Найдите угол между радиусами OA и OB окружности, если расстояние от центра O окружности до хорды AB в 2 раза меньше: 1) длины хорды AB ; 2) радиуса окружности.

522. В окружности провели диаметр AB и хорды AC и CD так, что AC = 12 см, ∠ BAC = 30°, AB ⊥ CD . Найдите длину хорды CD .

523. Через точку M к окружности с центром O провели касательные MA и MB , A и B — точки касания, ∠ OAB = 20°. Найдите ∠ AMB .

524. Через концы хорды AB , равной радиусу окружности, провели две касательные, пересекающиеся в точке C . Найдите ∠ ACB .

525. Через точку C окружности с центром O провели касательную к этой окружности, AB — диаметр окружности. Из точки A на касательную опущен перпендикуляр AD . Докажите, что луч AC — биссектриса угла BAD .

526. Прямая AC касается окружности с центром O в точке A (рис. 296). Докажите, что угол BAC в 2 раза меньше угла AOB .

527. Отрезки AB и BC — соответственно хорда и диаметр окружности, ∠ ABC = 30°. Через точку A провели касательную к окружности, пересекающую прямую BC в точке D . Докажите, что ∆ ABD — равнобедренный.

528. Известно, что диаметр AB делит хорду CD пополам, но не перпендикулярен ей. Докажите, что CD — также диаметр.

529. Найдите геометрическое место центров окружностей, которые касаются данной прямой в данной точке.

530. Найдите геометрическое место центров окружностей, которые касаются обеих сторон данного угла.

531. Найдите геометрическое место центров окружностей, которые касаются данной прямой.

532. Прямые, касающиеся окружности с центром O в точках A и B , пересекаются в точке K , ∠ AKB = 120°. Докажите, что AK + BK = OK .

533. Окружность касается стороны AB треугольника ABC в точке M и касается продолжения двух других сторон. Докажите, что сумма длин отрезков BC и BM равна половине периметра треугольника ABC .

534. Через точку C проведены касательные AC и BC к окружности, A и B — точки касания (рис. 297). На окружности взяли произвольную точку M , лежащую в одной полуплоскости с точкой C относительно прямой AB , и через неё провели касательную к окружности, пересекающую прямые AC и BC в точках D и E соответственно. Докажите, что периметр треугольника DEC не зависит от выбора точки M .

Упражнения для повторения

535. Докажите, что середина M отрезка, концы которого принадлежат двум параллельным прямым, является серединой любого отрезка, который проходит через точку M и концы которого принадлежат этим прямым.

536. Отрезки AB и CD лежат на одной прямой и имеют общую середину. Точку M выбрали так, что треугольник AMB — равнобедренный с основанием AB . Докажите, что ∆ CMD также является равнобедренным с основанием CD .

537. На стороне MK треугольника MPK отметили точки E и F так, что точка E лежит между точками M и F , ME = EP , PF = FK . Найдите угол M , если ∠ EPF = 92°, ∠ K = 26°.

538. В остроугольном треугольнике ABC проведена биссектриса BM , из точки M на сторону BC опущен перпендикуляр MK , ∠ ABM = ∠ KMC . Докажите, что треугольник ABC — равнобедренный.

Наблюдайте, рисуйте, конструируйте, фантазируйте

539. Установите закономерность форм фигур, изображённых на рисунке 298. Какую фигуру надо поставить следующей?

💡 Видео