Как доказать что прямые параллельны задачи (6 видео)

Как доказать что прямые параллельны задачи

Содержание

ПРИМЕРЫ РЕШЕНИЯ ОПОРНЫХ ЗАДАЧ:
2 Комментарии
Добавить комментарий Отменить ответ
Конспекты по геометрии:
7 класс
8 класс
9 класс
Найти конспект:
О проекте
Геометрия. 7 класс
Параллельность прямых
Определение параллельности прямых
Свойства и признаки параллельных прямых
Задача 1
Задача 2
🎦 Видео

ПРИМЕРЫ РЕШЕНИЯ ОПОРНЫХ ЗАДАЧ:

Задача № 1. Дано: AB = BC, ∠BAC = ∠CAD. Доказать: BC ∥ AD.

Задача № 2. Дано: ΔABC = ΔDEF, AC и DF лежат на одной прямой. Доказать: 1) BC ∥ EF, 2) AB ∥ DE.

Задача № 3. Дано: ∠1 = 61, ∠3 = 119, c ∩ a, c ∩ b. Доказать: a ∥ b.

Задача № 4. Дано: a ∥ b, c ∩ a, c ∩ b, ∠1 + ∠4 = 110°. Найти: ∠2, ∠3.

Задача № 5. Дано: ∠1 = ∠2, ∠4 = 130°. Найти: ∠3.

Задача № 6. Дано: AB ∥ CD, AB = BC, ∠ABF = 45°. Найти: ∠ACD.

Это конспект по теме «ЗАДАЧИ по теме Параллельные прямые». Выберите дальнейшие действия:

2 Комментарии

Супер
Но было бы хорошо, если бы можно было скачать

Спасибо. Все четко, ясно и понятно.

Добавить комментарий Отменить ответ

Конспекты по геометрии:

7 класс

Начальные геометрические понятия
Аксиомы планиметрии
Угол. Смежные и вертикальные углы
Опорные задачи по теме УГЛЫ
Параллельные прямые
ЗАДАЧИ по теме Параллельные прямые
Перпендикулярные прямые
Треугольник. Равенство треугольников
ЗАДАЧИ на Признаки равенства треугольников
Равнобедренный треугольник + ЗАДАЧИ
Свойства сторон и углов треугольника + ЗАДАЧИ
Прямоугольный треугольник
ЗАДАЧИ по теме Прямоугольные треугольники
Расстояние от точки до прямой (ЗАДАЧИ)
Геометрия 7 ЗАДАЧИ на построение
Мерзляк Геометрия 7 Глава 1 Простейшие геометрические фигуры
Мерзляк Геометрия 7 Глава 2 Треугольники
Мерзляк Геометрия 7 Глава 3 Параллельные прямые. Сумма углов Δ
Мерзляк Геометрия 7 Глава 4 Окружность и круг. Геометрические построения
Краткий курс геометрии 7 класс
Прямая. Окружность. Угол (опорный конспект)
Задачи по теме «Прямая. Окружность. Угол»
Треугольники (опорный конспект)
Ключевые задачи по теме Треугольники
Параллельные прямые (опорный конспект)
Ключевые задачи про Параллельные прямые
Сумма углов треугольника (опорный конспект)
Ключевые задачи по теме: Сумма углов треугольника

8 класс

Ломаная. Многоугольник + ЗАДАЧИ
Четырехугольник и его свойства
Параллелограмм: свойства и признаки
ЗАДАЧИ по теме Параллелограмм
Прямоугольник и его свойства
ЗАДАЧИ по теме Прямоугольники
Ромб и его свойства
ЗАДАЧИ по теме Ромб
Квадрат и его свойства
ЗАДАЧИ по теме Квадрат
Трапеция и её свойства
Средняя линия треугольника
Центральный угол. Вписанный угол
Описанная и вписанная окружности четырехугольника
Мерзляк Геометрия 8 Глава 1 Четырехугольники
Краткий курс геометрии 8 класс
Мерзляк Геометрия 8 Глава 2 Подобие треугольников
Мерзляк Геометрия 8 Глава 3
Мерзляк Геометрия 8 Глава 4 Многоугольники
Площадь ромба. Формулы и Калькулятор
Геометрия 8 Погорелов: все теоремы и определения

9 класс

Опорный конспект 1. Окружности
Опорный конспект 2. Описанные и вписанные окружности
Опорный конспект 3. Теорема синусов. Теорема косинусов
Опорный конспект 4. Правильные многоугольники

Найти конспект:

О проекте

Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Возрастная категория: 12+

(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!

Видео:Параллельные прямые (задачи).Скачать

Геометрия. 7 класс

Конспект урока

Признаки параллельности прямых

Перечень рассматриваемых вопросов:

Параллельные прямые.
Накрест лежащие, соответственные, односторонние углы.
Признаки параллельности прямых.
Решение задач на доказательство параллельности прямых.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

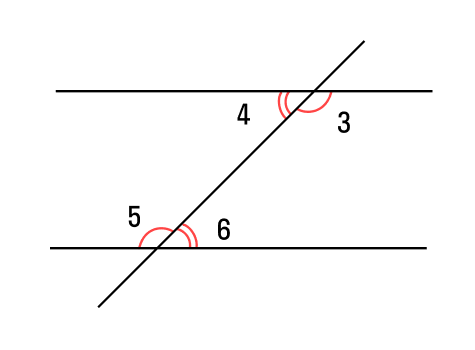
Вы уже знаете, что при пересечении двух прямых секущей образуются углы:

накрест лежащие: 3 и 6, 4 и 5.
односторонние: 3 и 5, 4 и 6.
соответственные: 1 и 5, 3 и 7, 2 и 6; 4 и 8.

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Рассмотрим и докажем признаки параллельности прямых.

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠ 1= ∠ 2 ≠ 90°

1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH₁, равный отрезку AH и проведем отрезок OH₁.

2) AO = OB т. к. O середина AB; AH = BH₁ по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH₁B по первому признаку равенства треугольников.

Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H₁ лежит на продолжении луча OH. Это значит, что точки H₁, O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН₁, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.

∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.

∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Разбор заданий тренировочного модуля.

Дано: ∠1= 60°, ∠2 = 120°.

∠2 и ∠3 смежные, ∠3 = 180° – 120° = 60° по свойству смежных углов;
∠3 = ∠1, это накрест лежащие углы;
Значит, прямые a и b параллельны по 1 признаку параллельности прямых.

Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.

Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.

Докажите: AB ║ CD.

∠A = ∠C = 60° – углы при основании равнобедренного Δ–ка равны.
∠BCK и ∠С смежные. ∠BCK = 180° – 60°= 120° – по свойству смежных углов.
∠BCD = ∠CDK = 60° т. к. CD – биссектриса делит угол пополам.
Значит, ∠A = ∠DCK = 60° ‑ соответственные, следовательно, AB║CD по 2 признаку параллельности прямых.

Ответ: AB║CD по 2 признаку параллельности прямых.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельность прямых

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Задачи на доказательство по геометрии. Признаки параллельности прямых.Скачать

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

два внутренних накрест лежащих угла равны между собой:

два соответственных угла равны между собой:

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.