В «Квантике» № 5, 2016 была опубликована задача:
Робот-пылесос, имеющий форму круга, проехал по плоскому полу. Для каждой точки граничной окружности робота можно указать прямую, на которой эта точка оставалась в течение всего времени движения. Обязательно ли и центр робота оставался на некоторой прямой в течение всего времени движения?
Удивительно, но ответ отрицателен — центр мог двигаться не по прямой! Мы дадим несколько решений, начнём издалека, зато узнаем по дороге много интересного. Решение в движении смотрите в мультфильме «Котёнок на лестнице».
Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Квантик на лестнице
Пусть к стене вертикально приставлена лестница, на середине которой неподвижно сидит Квантик (вид сбоку показан на рисунке 1). Лестница съезжает — нижний конец движется по полу вправо, а верхний движется по стене вниз (рис. 2), — пока не ляжет на пол (рис. 3). По какой линии движется Квантик?
Пусть О — точка под лестницей, в которой стыкуются стена и пол. Заметим, что и в начале, и в конце пути Квантик находится от точки O на одном и том же расстоянии, равном половине длины лестницы.
А что будет в любом промежуточном положении (рис. 4)? Достроим треугольник AOB до прямоугольника OACB. Квантик находится в точке пересечения диагоналей этого прямоугольника (рис. 5). Так как диагонали равны и точкой пересечения делятся пополам, OK — это половина AB. Получается, что расстояние от Квантика до точки O всегда одно и то же.
Значит, Квантик всё время находится на окружности с центром в точке O и радиусом длиной в половину лестницы, более точно — на четверти этой окружности (синяя линия на рисунке 6).
В каждой ли точке этой линии Квантик побывает? Очевидно, что да: Квантик движется «непрерывно» и не может «пропустить» какую-то точку синей дуги. Можно даже для каждой точки K на дуге нарисовать соответствующее положение лестницы: продлеваем OK до OC (удваивая) и достраиваем до прямоугольника.
Итак, путь Квантика — четверть окружности (рис. 6).
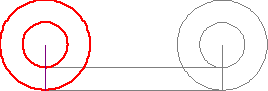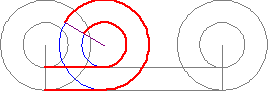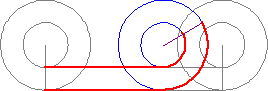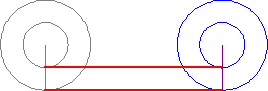
Но при чём здесь задача о круглом пылесосе? Прикрепим к лестнице пылесос, ограниченный красной окружностью (рис. 7) так, чтобы лестница была диаметром этой окружности (Квантик тогда сидит в её центре). Вместе со съезжающей лестницей-диаметром будет двигаться и окружность. При этом две точки окружности — концы лестницы, — будут перемещаться по прямым (стене и полу), а центр окружности (Квантик) — не по прямой, а по дуге!
Видео:Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Одна окружность катится по другой
Оказывается, и остальные точки красной окружности будут двигаться по прямым. Чтобы доказать это, нам понадобится ещё одна окружность — с центром в точке O и радиусом, равным длине лестницы (она отмечена зелёным на рисунке 8). Сейчас мы докажем, что красная окружность будет просто катиться по зелёной (без проскальзывания). Рассмотрим, например, положение красной окружности, изображённое на рисунке 9: лестница NO переехала в положение AB, Квантик сидит в точке K (заметьте, что красная окружность всегда проходит через O). Удвоим отрезок OK, продлив его до OC. Точка С окажется одновременно и на красной, и на зелёной окружностях. Отметим середину L дуги AC (рис. 10). Ясно, что углы LKC и NOC равны (так как NO и LK параллельны). Поскольку радиус красной окружности в два раза меньше радиуса зелёной, красная дуга LC в два раза короче зелёной дуги NC (рис. 11). Но тогда вдвое большая, чем LC, красная дуга AC равна зелёной дуге NC.
Это и значит, что красная окружность катится по зелёной, не проскальзывая: зелёное расстояние от точки N до точки касания окружностей всегда равно красному расстоянию от A до точки касания. Но если какая-то точка красной окружности движется по прямой, то и остальные тоже — ведь красная окружность равномерно катится по зелёной, и все точки красной окружности равноправны. Чтобы узнать, по какой именно прямой движется конкретная точка X красной окружности, можно дождаться, когда X попадёт на зелёную окружность, и в этот момент соединить прямой O и Х.
Мы доказали теорему Коперника: если окружность катится по внутренней стороне вдвое большей окружности, то каждая точка катящейся окружности всё время остаётся на некоторой прямой.
Видео:Движение по окружности | задачи ЕГЭ по профильной математикеСкачать

Пылесос едет и вращается
Приведём более короткое решение исходной задачи — опишем другим способом, как должен двигаться пылесос (ограниченный красной окружностью).
Нарисуем на столе синюю окружность с центром в точке O и такого же радиуса, как у пылесоса. Запустим пылесос так, чтобы его центр K двигался равномерно по синей окружности, а сам пылесос при этом вращался: если центр пылесоса поворачивается вокруг O на некий угол, то сам пылесос поворачивается вокруг своего центра на тот же самый угол в обратную сторону.
При таком движении все точки красной окружности равноправны — достаточно про любую из них доказать, что она движется вдоль некоторой прямой. Пусть пылесос стартовал из положения, показанного на рисунке 12. Докажем, что точка C пылесоса (его верхняя точка в стартовом положении) движется по прямой, проходящей через O.
Пусть центр пылесоса (K) повернулся на угол α вокруг О (по часовой стрелке). Если бы пылесос не вращался вокруг своего центра, точка C по-прежнему находилась бы над K, то есть на вертикальной прямой, проходящей через K (эта воображаемая ситуация показана на рисунке 13). Но надо ещё повернуть точку C на угол α в обратную сторону. Где окажется C после этого?
Поскольку точка K синей окружности, лежавшая над её центром, повернувшись на угол α по часовой стрелке, переехала с левой вертикальной прямой на правую, то точка C, лежащая над центром точно такой же красной окружности, повернувшись на тот же самый угол α против часовой стрелки, переедет с правой вертикальной прямой на левую! Задача решена.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Интересный факт
Вернёмся к задаче про Квантика. А что, если он будет сидеть не на середине лестницы, а в какой-то другой её точке (не на концах)? Тогда траектория Квантика будет четвертью эллипса (рис. 14). Много других интересных фактов можно найти в книге Н. Б. Васильева и В. Л. Гутенмахера «Прямые и кривые» (М.: МЦНМО, 2016), по мотивам введения к которой и написана эта статья.
Задачи для самопроверки
В задачах 1–3 красная окружность катится изнутри по зелёной окружности вдвое большего радиуса.
- Пусть в начальный момент времени наши окружности касались друг друга в точке N красной окружности. Где будет находиться точка N, когда красная окружность «проедет» а) четверть зелёной окружности; б) две её четверти; в) три её четверти; г) всю зелёную окружность?
- Сколько оборотов сделает красная окружность вокруг своего центра, прокатившись один раз по всей зелёной окружности?
- Пусть в задаче 2 по красной окружности бежит муравей так, что он всё время находится у точки касания окружностей. Сколько раз он обежит красную окружность по периметру?
- Прикрепим к съезжающей лестнице на рисунке 1 произвольный прямоугольный треугольник так, чтобы лестница была его гипотенузой. Как будет двигаться вершина прямого угла?
- а) На столе лежит пятак (монета достоинством 5 рублей). Ещё один пятак прокатывается по внешней стороне этого пятака (без проскальзывания). Сколько оборотов он сделает относительно своего центра, вернувшись в исходное положение?
б) Решите ту же задачу, если на столе лежат два пятака, касаясь друг друга, а третий пятак прокатывается по их внешней стороне, касаясь их по очереди.
в) А сколько оборотов сделает пятак, прокатываясь по внешней стороне трёх пятаков, касающихся друг друга?
Видео:Как искать точки на тригонометрической окружности.Скачать

Новое в блогах
Видео:ЕГЭ задание 16Скачать

Парадокс Аристотеля о движении двух колес
Имеем два колеса разного размера, расположенных одно в другом. Оба колеса синхронно катятся и проходят определённое расстояние. Смысл парадоксе ясен из картинки: два скрепленных колеса разного радиуса проходят тот же путь при полном обороте.
Если вы внимательно посмотрите на гифку вверху, то заметите – оба колеса полностью совершают оборот по всей своей окружности, чтобы преодолеть одно и то же расстояние (см. на красную линию). А также очевидно, что одна окружность меньше другой. Это означает, что, либо колёса имеют одинаковую окружность (что в корне неверно), либо разные окружности «разворачиваются» на одинаковую длину (чего быть никак не может).
А если представить, что всё это правда? Тогда технически возможно, что колесо с окружностью в 2,54 сантиметра в состоянии пройти тот же путь за один оборот, что и колесо с окружностью, равной 1,6 километров.
Но такого просто не бывает. Длина окружности с меньшим радиусом не может быть равна длине окружности с большим радиусом. Так в чём же дело?
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Соприкасающиеся окружности катящиеся друг по другу без проскальзывания
Видео:Окружность данного радиуса, проходящей через две заданные точкиСкачать
Котёнок на лестнице
Переход между слайдами — стрелочками.
Лестница, стоявшая на гладком полу у стены, соскальзывает вниз (всё время касаясь стены). По какой линии движется котёнок, сидящий на середине лестницы?
Лестница, стоявшая на гладком полу у стены, соскальзывает вниз (всё время касаясь стены). По какой линии движется котёнок, сидящий на середине лестницы?
Возникает предположение: искомая линия — дуга окружности. Но как это доказать?
Достроим треугольник из лестницы и угла до прямоугольника.
Диагонали прямоугольника равны и делятся точкой пересечения пополам.
То есть можно считать, что котёнок сидит на середине зелёной лестницы, конец которой закреплён у стены.
Итак, мы доказали, что котёнок движется по окружности.
Перейдём к другой задаче, на первый взгляд никак не связанной с первой.
По неподвижной окружности, касаясь её изнутри, катится без проскальзывания окружность вдвое меньшего радиуса.
По неподвижной окружности, касаясь её изнутри, катится без проскальзывания окружность вдвое меньшего радиуса.
По какой траектории движется фиксированная точка на меньшей окружности?
По неподвижной окружности, касаясь её изнутри, катится без проскальзывания окружность вдвое меньшего радиуса.
По какой траектории движется фиксированная точка на меньшей окружности?
Ответ в этой задаче до удивления простой: точка движется по прямой — а точнее, по диаметру неподвижной окружности.
(Этот результат называется теоремой Коперника.)
В некоторый момент окружности коснутся в отмеченной точке. Обозначим через $A$ соответствующую точку на большой окружности.
Прокатим ещё немного меньшую окружность.
Так как проскальзывания нет,
синие дуги одинаковой длины.
Раз длины дуг $KT$ и $AT$ равны, а радиус подвижной окружности вдвое меньше, $angle KQT=2angle AOT$.
А $angle KOT$ по теореме о вписанном угле вдвое меньше, $angle KOT=angle AOT$. То есть точка $K$ лежит на радиусе $OA$.
Это рассуждение работает вплоть до момента, когда точка $K$ совпадает с точкой $O$.
Это рассуждение работает вплоть до момента, когда точка $K$ совпадает с точкой $O$. В этот момент угол $AKT$ становится прямым.
Дальше длина синей дуги становится больше половины длины меньшей окружности, и наше рассуждение нуждается в небольшой модификации.
Мы получаем, что $angle KOT=180^circ-angle AOT$
и точка $K$ всё равно лежит на прямой $AO$.
Теорема Коперника доказана.
Оказывается, теорема Коперника непосредственно связана с задачей про котёнка на лестнице!
Посмотрим как соскальзывает стоящий у стены угольник.
Посмотрим как соскальзывает стоящий у стены угольник.
Мы уже знаем, что середина его гипотенузы движется по окружности.
А как движется вершина его прямого угла?
Посмотрим как соскальзывает стоящий у стены угольник.
Докажем, что вершина его прямого угла движется по прямой.
Опишем вокруг угольника окружность. Как следует из задачи про котёнка, она проходит через начало координат.
Поэтому два отмеченных угла равны как вписанные. А раз угол между стеной и направлением на синюю точку постоянен (он равен углу угольника), она движется по прямой.
Добавим на рисунок окружность вдвое большего радиуса.
Когда маленькая окружность катится по большой, чёрные вершины едут по «стене» и «полу» в силу теоремы Коперника.
Когда маленькая окружность катится по большой, чёрные вершины едут по «стене» и «полу» в силу теоремы Коперника.
Когда маленькая окружность катится по большой, чёрные вершины едут по «стене» и «полу» в силу теоремы Коперника.
По той же причине синяя вершина также движется по прямой.
Котёнок теперь сидит в центре меньшей окружности (который, очевидно, движется по окружности).
Котёнок теперь сидит в центре меньшей окружности (который, очевидно, движется по окружности).
А какую фигуру при таком движении заметает вся лестница?
А какую фигуру при таком движении заметает вся лестница?
А какую фигуру при таком движении заметает вся лестница?
Видно, что это совсем не вся внутренность окружности.
Кривая, ограничивающая это множество точек, — астроида.
Кривая, ограничивающая это множество точек, — астроида.
Она получается как траектория точки, если катать внутри большой окружности окружность вчетверо меньшего радиуса.
Об астроиде и о том, почему она появляется в этой задаче, тоже можно узнать из книги «Прямые и кривые».
по мотивам книги «Прямые и кривые»
Н. Б. Васильева и В. Л. Гутенмахера.
Картинки — М. Панов.
Разговоры — Г. Мерзон, М. Панов.
🔥 Видео
Задача про трапецию, описанную около окружностиСкачать

✓ Радиус описанной окружности | ЕГЭ. Задание 1. Математика. Профильный уровень | Борис ТрушинСкачать

Пропорциональные отрезки круга. 9 класс.Скачать

Внешнее сопряжение дуги и прямой дугой заданного радиуса. Урок16.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Теорема о числе точек пересечения двух окружностейСкачать

Тригонометрия с нуля до ЕГЭ за 6 часов | Математика ЕГЭ 10 класс | УмскулСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Задачи на движение по окружности. ЕГЭ по математике 2020Скачать

Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать