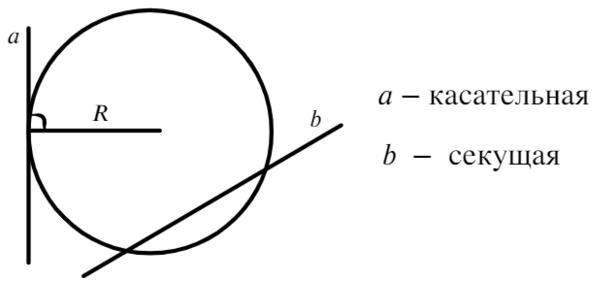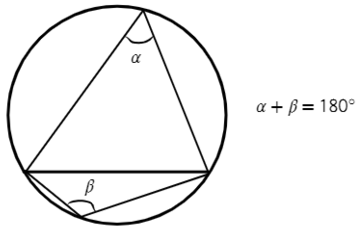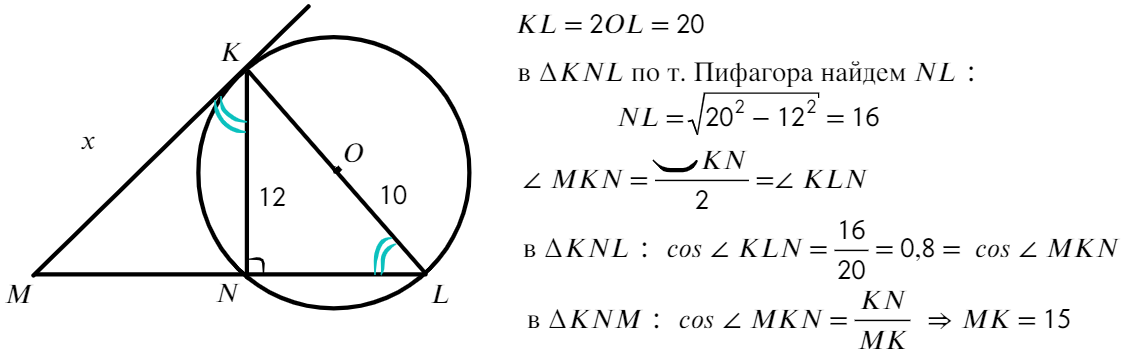На ЕГЭ и ОГЭ запрещено брать циркуль, но обычную деревянную линейку взять можно.
Что необходимо сделать:
1. В линейке заранее просверливаем несколько отверстий на нужном вам расстоянии.
2. Берём на экзамен эту линейку и две чёрные ручки, желательно капиллярные у них стержень тоньше и длиннее.
3. Перед экзаменом стоит несколько раз потренироваться рисовать окружности.
4. Рисуем ровные окружности на экзамене.
- Как строить чертежи в задачах по стереометрии
- Теория и практика окружности
- Аналогично в каждом отрезке присутствует точка, вне окружности (О).
- Задача №1. Дано на рисунке:
- Достаточно вспомнить свойства центральных и вписанных углов.
- Ответ: 39°
- Задача №2. Дано на рисунке:
- Найти нужно меньшую дугу BD
- Ответ: 100°
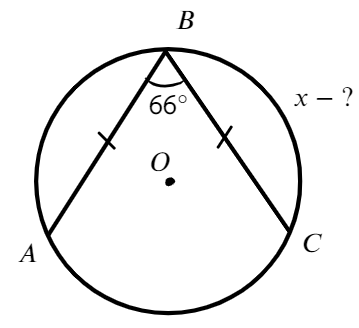
- Найти меньшую дугу ВС
- Ответ: 114°
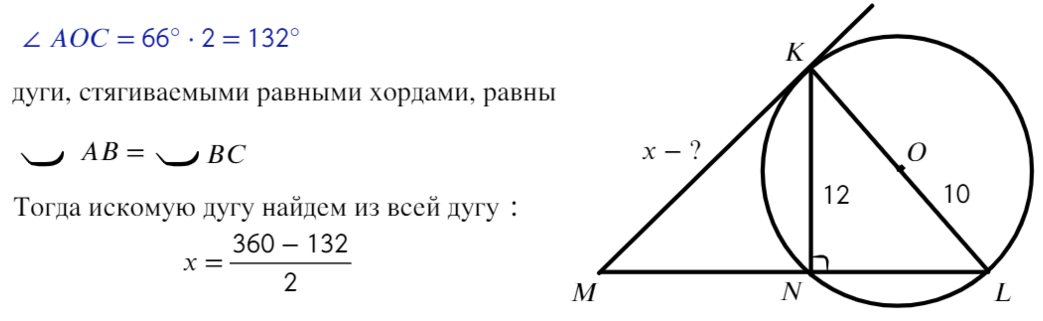
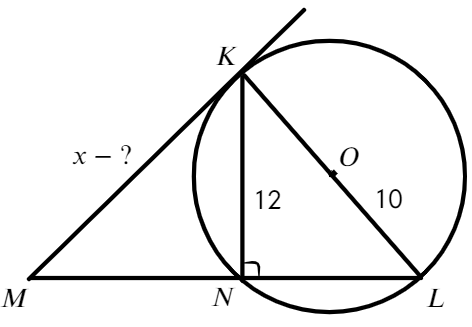
- Задача №4. Дано на рисунке:
- Найти отрезок МК
- Ответ: МК = 15.
- Задача №5. Дано на рисунке:
- Попробуй найти подобные треугольники
- Ответ: 6
- Задача №5. Дано на рисунке:
- Без свойства секущей и касательной здесь будет тяжело
- Ответ: 12√7.
- Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
- О треугольниках О четырехуголниках
- 📺 Видео
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Как строить чертежи в задачах по стереометрии
Мы рассказали о том, что такое параллельное проецирование и как строить чертежи объемных тел. Однако часто бывает так, что вы построили чертеж — и непонятно, что делать дальше. На чертеже ничего хорошего не видно. Почему?
Не спешите обвинять себя в отсутствии пространственного мышления. Может быть, просто ракурс выбран неудачно.
Очень важно, чтобы объемное тело на вашем чертеже выглядело действительно объемным, а не складывалось, как зонтик. Следите, чтобы одна грань не накладывалась на другую, а непараллельные отрезки (например, ребро куба и его диагональ) не совпадали.
Приведем примеры удачных и неудачных чертежей.
Мы рисуем чертеж крупным, чтобы на нем всё было хорошо видно. Не стоит, как «лучший в мире рисовальщик петухов» Карлсон, изображать крошечного одинокого петушка (или малюсенький кубик) в углу тетради.
Видимые линии изображаем сплошными, невидимые — штриховыми. Если вы решаете задачу векторно-координатным методом, ставьте рядом с точками их координаты. Это удобно.
Иногда одного чертежа недостаточно. Чаще всего для решения задач по стереометрии, кроме «объемного» чертежа, нужен один или несколько плоских.
Видео:Как нарисовать идеальную окружность без циркуля на ЕГЭ 2022 по математике?Скачать

Теория и практика окружности
Свойства касательных и секущих.
Площадь, сектор, длина окружности.
Задачи на окружности.
По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!
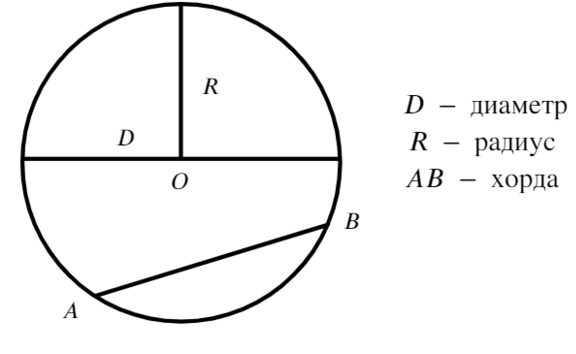
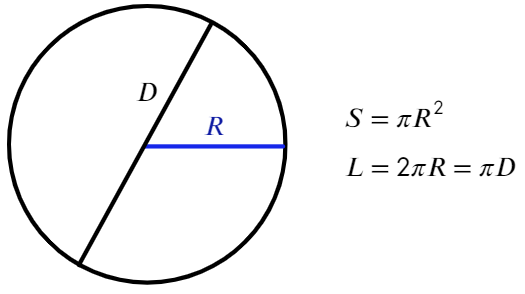
Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.
В окружности может быть проведено 3 типа отрезка:
Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).
Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).
Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).
А также две прямые снаружи от окружности:
Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.
Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.
Теперь чуть-чуть об углах и дугах:
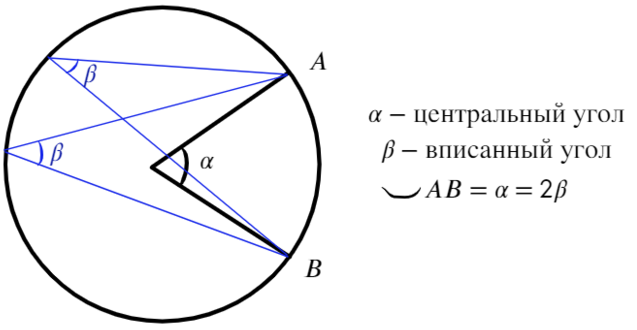
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.
Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.
Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.
Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.
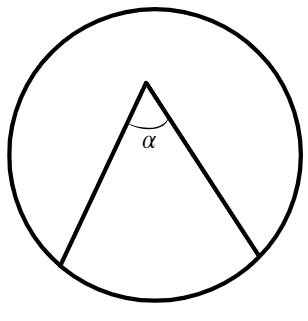
А вот такой угол НЕвписанный, такой угол «никто и звать никак».
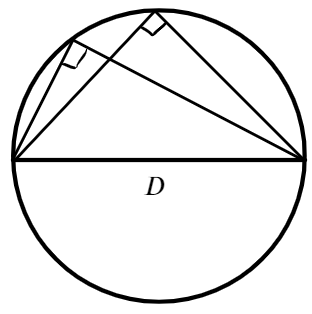
Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:
Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.
Запишем основные свойства углов в окружности:
Нашел что-то общее?
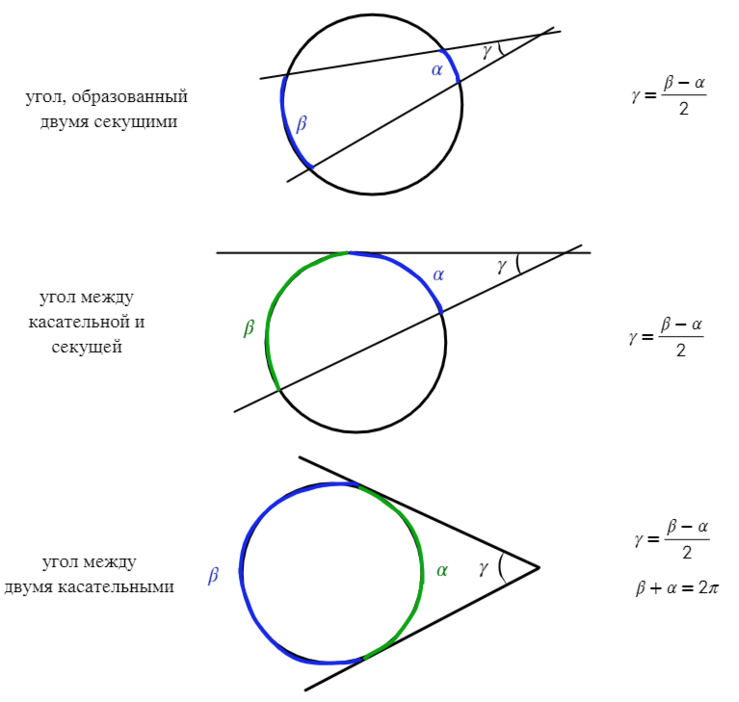
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.
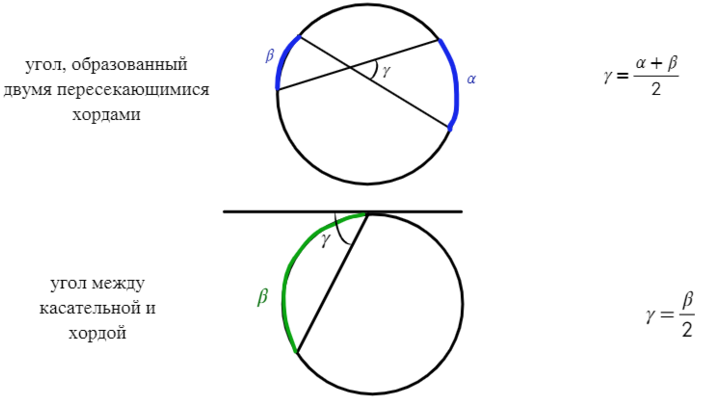
Если угол находится внутри окружности, то находим его через полусумму дуг.
Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.
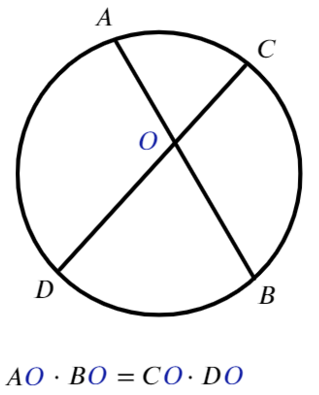
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:
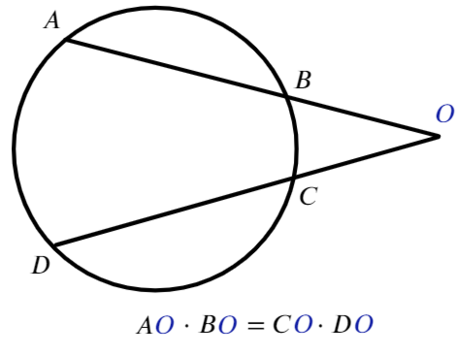
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:
Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).
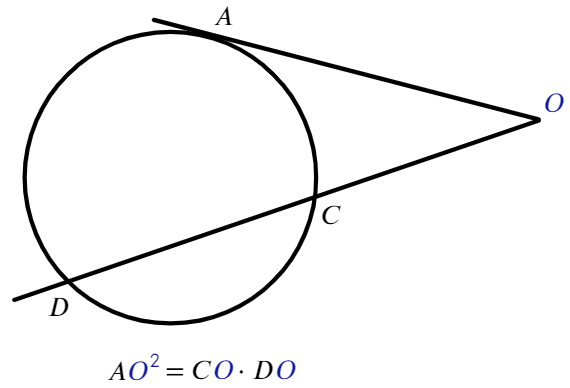
Если из точки, лежащей вне окружности, проведены касательная и секущая:
Аналогично в каждом отрезке присутствует точка, вне окружности (О).
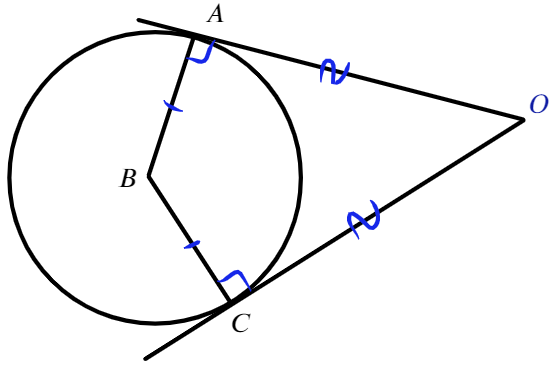
Если теперь провести две касательные из точки O, то получим такие равные отрезки:
Касательные равны, как, сообственно, и радиусы!
Площадь и длина окружности находятся по формуле:
По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD
Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!
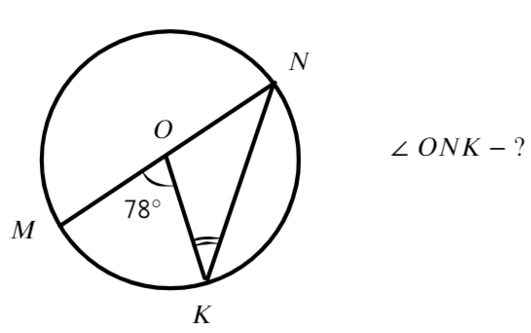
Задача №1. Дано на рисунке:
Достаточно вспомнить свойства центральных и вписанных углов.
Ответ: 39°
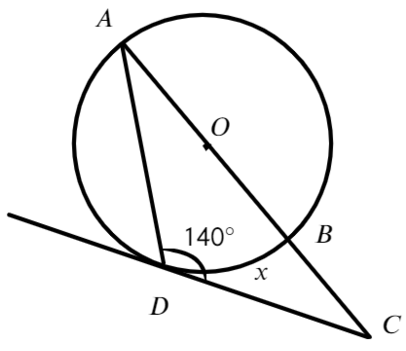
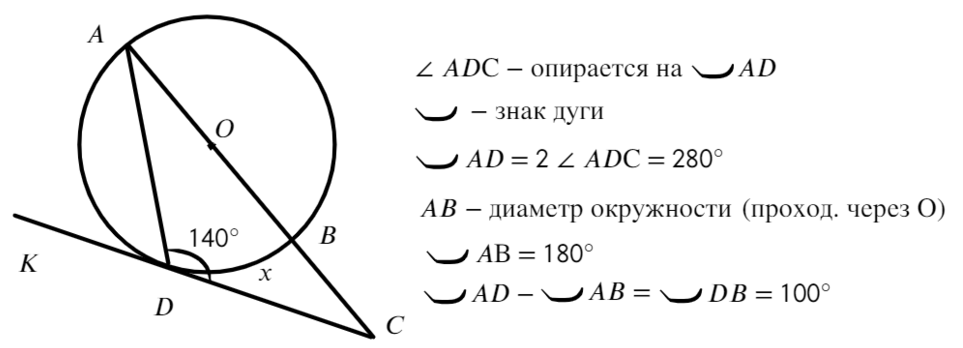
Задача №2. Дано на рисунке:
Найти нужно меньшую дугу BD
Ответ: 100°
Задача №3. Дано на рисунке:
Найти меньшую дугу ВС
Ответ: 114°
Задача №4. Дано на рисунке:
Найти отрезок МК
Ответ: МК = 15.
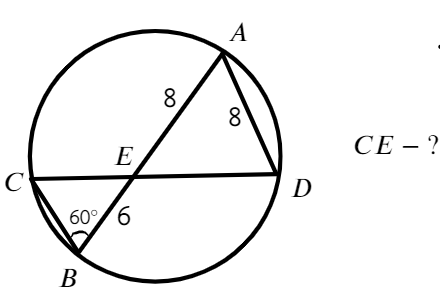
Задача №5. Дано на рисунке:
Попробуй найти подобные треугольники
Ответ: 6
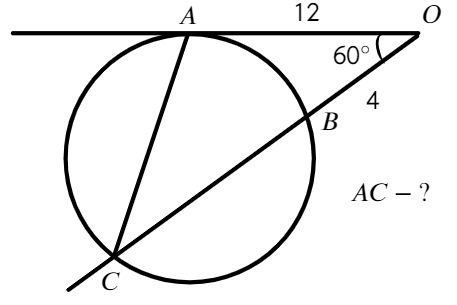
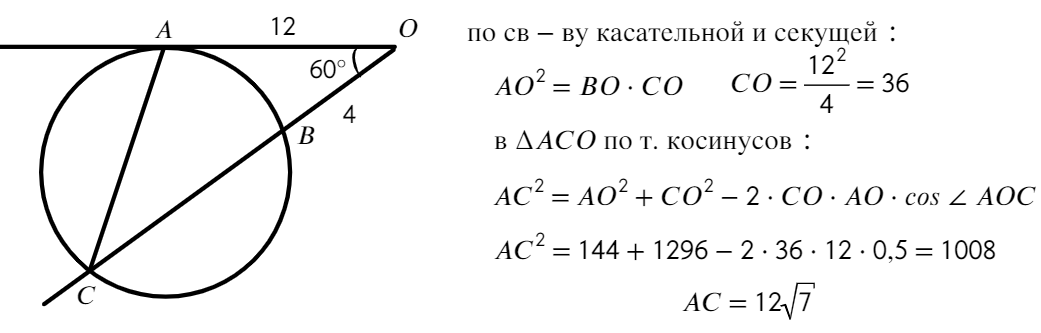
Задача №5. Дано на рисунке:
Без свойства секущей и касательной здесь будет тяжело
Ответ: 12√7.
Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
О треугольниках
О четырехуголниках
p.s. Не бойся ошибаться и задавать вопросы!
Если нашел опечатку, или что-то непонятно − напиши.
📺 Видео
🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Тригонометрическая окружность. Как выучить?Скачать

ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Как на ЕГЭ нарисовать окружность без циркуля?Скачать

Как запомнить тригонометрический круг специально ничего не выучивая?Скачать

ТОП-3 конструкции с окружностями для №16 из ЕГЭ 2023 по математикеСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

Тригонометрическая окружность. Задание 13 | Математика ЕГЭ | УмскулСкачать

Открытый вебинар: «Параметры для 100 баллов за 5 месяцев до ЕГЭ. Часть 2»Скачать

движение по кругу | математика ЕГЭ | ВебиумСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Важна формула про секущую и касательную на ОГЭ и ЕГЭСкачать

Школа для родителей. Циркуль, окружность, радиус, диаметр.Скачать

Окружности №1 в ЕГЭ | Профильная математика ЕГЭ 2024 | УмскулСкачать

Уравнение окружности (1)Скачать