К окружности вписанной в треугольник авс проведена касательная пересекающая

Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Условие

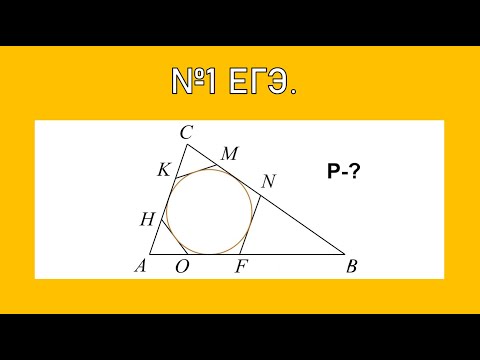
К окружности, вписанной в правильный треугольник ABC , проведена касательная, пересекающая стороны AC и BC в точках M и N соответственно и касающаяся окружности в точке T .

а) Докажите, что периметр треугольника MNC равен стороне треугольника ABC .

б) Найдите MT:TN, если известно, что CM: MA=1:4.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Решение

а) Пусть K и L — точки касания окружности и сторон BC и AC соответственно.

Так как MT=ML и NK=NT как отрезки касательных, проведенных из одной точки, то

P_= CM+MT+TN+NC= CM+ML+KN+NC= CL+KC.

Так как ABC — правильный треугольник, то CL=KC=frac. Следовательно, P_=AC, что и требовалось доказать.

б) 1 . Обозначим TN=x, CM=a. Так как CM:MA=1:4 по условию, то MA=4a и AC=5a.

Тогда CL=frac=fraca и ML=CL-CM=fraca-a=fraca. Так как ML=MT, то MT=fraca. Тогда MN=MT+TN=fraca+x.

Так как NT=NK, то NK=x. Тогда CN=CK-NK=frac-x=fraca-x.

2. По теореме косинусов для треугольника MNC

MN^2=CN^2+CM^2- 2 cdot CN cdot CM cdot cos angle NCM. Подставляя в это уравнение выражения для сторон треугольника MNC , получим:

left ( fraca+xright )^2= left ( fraca-xright )^2+a^2-2left ( fraca-xright )a cos 60^circ;

fraca^2+2 cdot fracax+x^2= fraca^2-2 cdot fracax+x^2+a^2- 2left ( fraca-x right )a cdot frac;

Видео:Решение задачи №1 из ЕГЭ математикаСкачать

К окружности вписанной в треугольник авс проведена касательная пересекающая

БАЗА ЗАДАНИЙ

Задание № 16. Планиметрия с доказательством.

1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.

2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3

3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2.
Ответ: б) 18√3

4. В треугольнике ABC точки A ₁ , B ₁ , C ₁ — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A₁, B₁, C₁, H— лежат на одной окружности.
б) Найдите A₁ H, если BC = 2√3.

5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10

6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4

7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6

8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.

9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.

10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.

11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88

12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC = 55°.

13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.

14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C ₁ , B ₁ соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB ₁ C ₁ .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B ₁ C ₁ =6 и площадь треугольника AB ₁ C ₁ в восемь раз меньше площади четырёхугольника BCB ₁ C _{1 .}

15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.

16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.

17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65

18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4

19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC = (KL+KM-LM)/2 .

б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2

20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3

21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1

22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36

23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4

24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.

25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.

26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.

27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.

28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.

Видео:✓ Простое решение красивой геометрии | Планиметрия | Физтех-2021. Математика | Борис ТрушинСкачать

К окружности, вписанной в трегольник ABC, проведена касательная, пересекающая стороны AC и BC в точках P и Q соответственно?

Геометрия | 5 — 9 классы

К окружности, вписанной в трегольник ABC, проведена касательная, пересекающая стороны AC и BC в точках P и Q соответственно.

Известно, что AB = 33, а периметр треугольника ABC равен 103.

НАйти периметр треугольника CPQ.

Нашел чему равно PQ.

К. PN = PK и KQ = QM (по свойству касательных), то СN + CM = P треуг.

AN = AL и MB = BL, то AN + NB = AB (по св — ву касательных)

ABC = AB + BC + AC, где BC = CM + MB ; AC = CN + AN

Получим : AB + CM + MB + CN + AN = 103 (выделенные величины равно, поэтому их складываем)

AB + 2CM + MB + AN = 103 (см.

Отсюда CM = 51, 5 — 33 = 18, 5

CN + CM = P треуг.

СPQ и CN = CM (по св — ву касат.

CPQ = 2CM = 2 * 18, 5 = 37.

Видео:ЕГЭ по математике. Задание №16 #11Скачать

Через середину P стороны AB треугольника ABC проведена прямая, параллельная стороне AC и пересекающая сторону BC в точке Q?

Через середину P стороны AB треугольника ABC проведена прямая, параллельная стороне AC и пересекающая сторону BC в точке Q.

Найдите длину стороны AC, если известно, что периметр треугольника ABC равен 54см, QC = 12см, а PQ в два раза больше, чем BP.

Видео:Разбор Задачи №16 из Работы СтатГрад от 19 апреля 2019Скачать

КАСАТЕЛЬНАЯ К ОКРУжНОСТИ , ВПИСАННОЙ В ТРЕУГОЛЬНИК ABC ПЕРЕСЕКАЕТ СТОРОНЫ ВС И АС СООТВЕТСТВЕННО В ТОЧКАХ А1 И В1 ?

КАСАТЕЛЬНАЯ К ОКРУжНОСТИ , ВПИСАННОЙ В ТРЕУГОЛЬНИК ABC ПЕРЕСЕКАЕТ СТОРОНЫ ВС И АС СООТВЕТСТВЕННО В ТОЧКАХ А1 И В1 .

НАЙДИТЕ ПЕРИМЕТР ТРЕУГОЛЬНИКА А1В1С1 ЕСЛИ ВС = 5, АС = 6 И АВ = 7 МОЖНО ТОЛЬКО ОТВЕТ БЕЗ РЕШЕНИЯ!

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Периметр треугольника ABC равен 8?

Периметр треугольника ABC равен 8.

В треугольник вписана окружность и к ней проведена касательная, параллельная стороне AB.

Отрезок этой касательной, заключённый между сторонами AC и CB, равен 1.

Найдите сторону AB.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В равнобедренный треугольник ABC вписана окружность, касающаяся боковых сторон треугольника в точках K и E?

В равнобедренный треугольник ABC вписана окружность, касающаяся боковых сторон треугольника в точках K и E.

Найдите периметр треугольника ABC, если хорда KE равна 12 см, а отрезок касательной, заключенной между боковыми сторонами и параллельный основанию, равен 10 см.

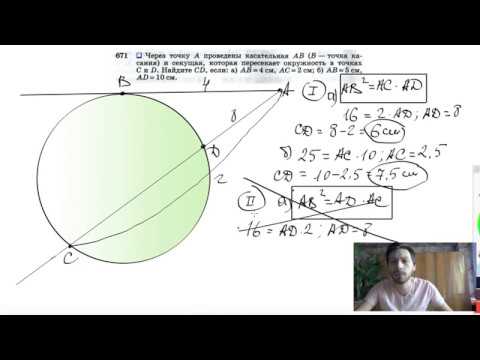
Видео:№671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекаетСкачать

Периметр треугольника ABC равен 12см, а длина диаметра окружности , вписанной в него , равна 6 см?

Периметр треугольника ABC равен 12см, а длина диаметра окружности , вписанной в него , равна 6 см.

Вычислите площадь треугольника ABC.

Видео:Геометрия К окружности, описанной около треугольника ABC, проведена в точке B касательнаяСкачать

Периметр треугольника abc равен 12 окружность касающаяся стороны AB и продолжение сторон AC и BC касается прямой АС в точке Р?

Периметр треугольника abc равен 12 окружность касающаяся стороны AB и продолжение сторон AC и BC касается прямой АС в точке Р.

К этой окружности проведена касательная параллельная прямой AB и пересекающая продолжение сторон АС и ВС в точках M и N так что MN = 3 НАйдите длину отрезка PQ где Q точка касания вписаной окружности треугольника ABC со стороной AC.

Видео:Задача по геометрии.Скачать

К окружнности, вписанной в треугольник ABC, проведены три касательные?

К окружнности, вписанной в треугольник ABC, проведены три касательные.

Периметры отсеченных треугольников равны 10, 12, 7.

Найдите периметр данного треугольника.

Видео:Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

Окружность радиуса 2, вписанная в треугольник ABC, касается средней линии треугольника, параллельной стороне BC?

Окружность радиуса 2, вписанная в треугольник ABC, касается средней линии треугольника, параллельной стороне BC.

Периметр треугольника ABC равен 24.

Найти стороны треугольника.

Видео:Задание 25. Тест 22. ОГЭ. Математика.Скачать

Точки T и O — соответственно середины AB и BC треугольника ABC?

Точки T и O — соответственно середины AB и BC треугольника ABC.

В треугольник BTO вписана окружность.

Вычислите длину радиуса окружности, если известно, что площадь треугольника TBO равна 12 см², а периметр треугольника ABC равен 16.

Видео:Задание 16 из ЕГЭ по математике. Профильный уровеньСкачать

Треугольник ABC – равносторонний?

Треугольник ABC – равносторонний.

Окружность, вписанная в этот треугольник, касается его сторон в точках M и N .

Длина дуги этой окружности равна 1.

Какой периметр имеет треугольник ABC?

На странице вопроса К окружности, вписанной в трегольник ABC, проведена касательная, пересекающая стороны AC и BC в точках P и Q соответственно? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

🎥 Видео

Окружность вписанная в прямоугольный треугольник АВС касается катетов АС и ВС в точках М и N соответСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

ОГЭ без рекламы математика 2021 задача 25 5 и 6 вариантыСкачать

Геометрия Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. НайдитеСкачать

#30. Регион ВсОШ 2023, 10.5Скачать

🔴 ВСЕ ЗАДАНИЯ 26 ИЗ ОТКРЫТОГО БАНКА (ВТОРАЯ ПОЛОВИНА ВСЕХ ЗАДАЧ) | ОГЭ 2017Скачать