Через вершины B и C треугольника ABC проходит окружность, пересекающая стороны AB и AC соответственно в точках K и M.
а) Доказать, что треугольники ABC и AMK подобны.
б) Найти MK и AM, если AB = 2, BC = 4, CA = 5, AK = 1.
а) Из свойств секущих к окружности известно:
Получаем, что треугольники ABC и AMK подобны (так как угол A — общий). Что и требовалось доказать.
б) Из подобия треугольников имеем:
Подставляя сюда известные значения, получим:
Ответ:
| Критерии оценивания выполнения задания | Баллы | |
|---|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 | |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 | |
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Содержание
Видео:ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать  math4school.ruВидео:Окружность вписанная в треугольник и описанная около треугольника.Скачать  ТреугольникиВидео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Основные свойства | ||
 | Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника). Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины. Внешним углом треугольника называется угол, смежный внутреннему углы треугольника. Сумма углов треугольника равна 180°: Внешний угол равен сумме двух внутренних углов, не смежных с ним, и больше любого внутреннего, с ним не смежного: Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол: | |
 | ||
 | Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны: У равных треугольников все соответствующие элементы равны (стороны, углы, высоты, медианы, биссектрисы, средние линии и т.д.) В равных треугольниках против равных сторон лежат равные углы, а против равных углов – равные стороны. | |
 | ||
 | ||
 | ||
 | Подобными называются треугольники, у которых соответствующие стороны пропорциональны. Коэффициент пропорциональности называется коэффициентом подобия: Два треугольника подобны, если:
У подобных треугольников соответствующие углы равны, а соответствующие отрезки пропорциональны: Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. | |
 | ||
 | ||
 | Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны. Три медианы треугольника пересекаются в одной точке, делящей медианы в отношении 2:1, считая от вершины:
| |
 | Длины медиан, проведённых к соответствующим сторонам треугольника, равны: Видео:ОГЭ 2021. Задание 24. Геометрическая задача на вычисление.Скачать  Биссектрисы треугольника | |
 | Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне. Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник. Биссектриса внутреннего угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные двум другим сторонам: Длина биссектрисы угла А : | |
 | ||
 | Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны. Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника. Высоты треугольника обратно пропорциональны его сторонам: Длина высоты, проведённой к стороне а : Видео:Окружность, построенная на стороне треугольника как на диаметреСкачать  Серединные перпендикуляры | |
 | Серединный перпендикуляр – это прямая, которая проходит через середину стороны треугольника перпендикулярно к ней. Три серединных перпендикуляра треугольника пересекаются в одной точке, которая является центром окружности, описанной около данного треугольника. Точка пересечения биссектрисы угла треугольника с серединным перпендикуляром противолежащей стороны лежит на окружности, описанной около данного треугольника. Видео:Задание 26 Теорема косинусов, окружность, вписанные углыСкачать  Окружность, вписанная в треугольник | |
 | Окружность называется вписанной в треугольник, если она касается всех его сторон. Точки касания вписанной окружности сторон треугольника отсекают от его сторон три пары равных между собой отрезков: Радиус вписанной в треугольник окружности – расстояние от её центра до сторон треугольника: Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  Окружность, описанная около треугольника | |
 | Окружность называется описанной около треугольника, если она проходит через все его вершины. Радиус описанной окружности: Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать  Расположение центра описанной окружности | |
 |  |  |
| Центр описанной окружности остроугольного треугольника расположен внутри треугольника. | Центр описанной окружности прямоугольного треугольника совпадает с серединой его гипотенузы. | Центр описанной окружности тупоугольного треугольника расположен вне треугольника. |
Видео:Вершины треугольника делят окружность на три дуги, длины которых относятся как 6:13:17Скачать  Равнобедренный треугольник | ||
 | Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника. В равнобедренном треугольнике углы при основании равны: ∠ A = ∠ C. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой, и высотой: BL – медиана, биссектриса, высота. | |
 | ||
 | Треугольник у которого все стороны равны называется равносторонним или правильным треугольником. Центры вписанной и описанной окружностей правильного треугольника совпадают. Все углы равностороннего треугольника равны: | |
 | ||
 | Треугольник называется прямоугольным, если у него есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой. Прямоугольные треугольники равны если у них равны:
| |
 | Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу: Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу: Высота прямоугольного треугольника, проведённая из вершины прямого угла, может быть определена через катеты и их проекции на гипотенузу: Медиана, проведённая из вершины прямого угла, равна половине гипотенузы: Высота прямоугольного треугольника, проведённая из вершины прямого угла, делит данный треугольник на два треугольника, подобные данному: Площадь прямоугольного треугольника можно определить через катеты: через катет и острый угол: через гипотенузу и острый угол: | |
 | ||
 | ||
 | ||
Три окружности, каждая из которых касается одной стороны (снаружи) и продолжений двух других сторон треугольника, называются вневписанными. Центр вневписанной окружности лежит не пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах. Так точка О1 , центр одной из вневписанных окружностей Δ ABC , лежит на пересечении биссектрисы ∠ A треугольника ABC и биссектрис BО1 и C О1 внешних углов Δ ABC при вершинах B и C . Таким образом, шесть биссектрис треугольника – три внутренние и три внешние – пересекаются по три в четырёх точках – центрах вписанной и трёх вневписанных окружностей. Δ ABC является ортоцентричным в Δ О1О2О3 (точки A , B и C – основания высот в Δ О1О2О3 ). В Δ ABC углы равны 180°–2 О1 , 180°–2 О2 , 180°–2 О3 . Радиус окружности, описанной около Δ О1О2О3 , равен 2 R , где R – радиус окружности, описанной около Δ ABC . Δ ABC имеет наименьший периметр среди всех треугольников, вписанных в Δ О1О2О3 . Если ra , rb , rс – радиусы вневписанных окружностей в Δ ABC , то в Δ ABC верно: для r – для R – для S – для самих ra , rb , rс – Видео:Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать  Теоремы синусов, косинусов, тангенсов; формулы Мольвейде | ||
 | Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности: Теорема тангенсов (формула Региомонтана): Видео:ОГЭ, задание 23 (геометрическая задача на вычисление). Треугольники, часть 2Скачать  Тема: «Применение конструкций треугольник-окружность в решении задач геометрии»Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов Сертификат и скидка на обучение каждому участнику Департамент образования города Москвы Государственное образовательное учреждение высшего профессионального образования МОСКОВСКИЙ ИНСТИТУТ ОТКРЫТОГО ОБРАЗОВАНИЯ Факультет повышения квалификации слушателя факультета повышения квалификации педагогических кадров отделения «Математика» Ивакина Нелля Павловна Тема: «Применение конструкций треугольник-окружность в решении задач геометрии» Заведующий кафедрой математики к.ф.-м.н. Ященко Иван Валериевич «04» апреля 2014г. г. Москва – 2014г. Вспомогательные конструкции и их свойства…………………………… 5 Треугольник и секущая, теорема Менелая ……………………………5 Треугольник и точка, теорема Чевы …………………………………. 7 Вписанный угол. Теорема синусов …………………………….………9 Окружность и касательная, окружность и секущая. Теоремы о свойствах секущих …………………………………………….….……11 Видео:Через вершины А и В треугольника АВС проведена окружность, касающаяся прямыхСкачать  Основные конструкции……………………………………………….….…14Видео:Задание 26 Две окружности, внешнее касаниеСкачать  2.1 Треугольник и описанная окружность………………………….….….142.2 Частные случаи: прямоугольный, равнобедренный и равносторонний треугольник ………………………………………………………….……. 15Треугольник и вписанная (вневписанная) окружность……….………17Задачи для самостоятельного решения. ………………………….………21 Список использованной литературы …………………………………………23 ВведениеПри решении многих задач планиметрии возникают различные конфигурации, в которых участвуют треугольник и окружность. Знание наиболее распространенных комбинаций и их свойств позволяет получать короткие и красивые решения сложных на первый взгляд задач. К таким конструкциям в первую очередь относятся «треугольник и описанная окружность», «треугольник и вписанная окружность», которые довольно подробно изучаются в школьном курсе, в меньшей степени изучаются конструкции «треугольник и вневписанная окружность», «треугольник и окружность, проходящая через две его вершины», «треугольник и окружность, касающаяся двух его сторон» и другие. Взгляд на планиметрию через призму конструкций дает учащимся возможность по-новому посмотреть на хорошо знакомый материал и связать его с новыми знаниями, укрепив их через практическое применение к решению задач. Предлагаемые темы рассчитаны на школьников 10-11 классов, при подготовке к сдаче ЕГЭ (выполнения заданий С4). Цель данных занятий: познакомить старшеклассников с различными конструкциями, в которых участвуют треугольник и окружность и свойствами этих конструкций, научить находить эти конструкции в ходе исследования условий задачи и применять нужные свойства для получения решения. Требования к уровню усвоения содержания предмета Старшеклассники должны знать: основные конструкции, описанные выше и связанные с ними факты и теоремы, ряд вспомогательных конструкций: «треугольник и секущая», «окружность и касательная», «треугольник и точка», «окружность и секущая» и их свойства. Старшеклассники должны уметь: определять, какие конструкции возникают в геометрических задачах, применять подходящие свойства этих конструкций для поиска решения. 1. Вспомогательные конструкции и их свойстваВ этой части мы рассмотрим некоторые важные конфигурации, в которых участвуют треугольник, окружность, прямая или угол. 1.1 Треугольник и секущая, теорема МенелаяСекущей будем называть прямую, которая пересекает некоторую геометрическую фигуру: треугольник, окружность, угол и т.п. Иногда удобно брать не только точки пересечения фигуры и секущей, но и некоторые дополнительные точки: например, точку пересечения прямой, на которой лежит сторона треугольника и секущей.
Теорема Менелая. Пусть Справедлива также обратная теорема Менелая. Теорема, обратная теореме Менелая. В треугольнике АВС точки А1, В1, С1 принадлежат прямым ВС, АС, АВ соответственно, тогда если Упражнение 1. Докажите теорему Менелая. (Указание: опустите на секущую перпендикуляры из вершин треугольника и рассмотрите пары получившихся подобных прямоугольных треугольников. Заменив в (1) отношения гипотенуз на отношения соответствующих катетов и выполнив сокращения, получите нужный результат.) Упражнение 2. Докажите теорему, обратную теореме Менелая. (Указание: воспользуйтесь методом «от противного». Предположите, что, например, точка A 1 не лежит на секущей. Тогда секущая пересечет сторону BC в некоторой точке A 2, для которой выполнена прямая теорема Менелая. Далее самостоятельно получите противоречие.) Р Построим треугольник DEF , где D , E , F – середины сторон, AB , AC и BC соответственно. (по теореме Менелая) Значит, по обратному утверждению теоремы Менелая точки K , L и M лежат на одной прямой, что и требовалось доказать. 1.2 Треугольник и точка, теорема Чевы Второй интересной конструкцией, которую мы рассмотрим, является треугольник, у которого три отрезка, проведенных из вершин на противоположные стороны или их продолжения, пересекаются в одной точке. Свойства этой конструкции описывает теорема Чевы. Т Так же, как и в случае теоремы Менелая, для теоремы Чевы справедливо обратное утверждение. Теорема, обратная теореме Чевы. Если в произвольном треугольнике АВС на сторонах ВС, СА, АВ или их продолжениях взяты соответственно точки А1, В1, С1, для которых выполнено условие то прямые АА1, ВВ1, СС1 пересекаются в одной точке. Упражнение 4. Докажите теорему Чевы. (Указание: попробуйте записать условие теоремы Менелая для треугольников ABB 1 и B 1 BC и секущих CC 1 и AA 1, а затем исключите из этих равенств «лишние» отрезки.) Упражнение 5. Докажите теорему, обратную теореме Чевы. (Указание: вновь используйте метод доказательства «от противного».) Упражнение 6. Решите задачу. На медиане СМ треугольника АВС дана точка Р, через которую проведены прямые АР и ВР, пересекающие стороны ВС и АС треугольника в точках А1 и В1 соответственно. Докажите, что если АА1 равно ВВ1, то данный треугольник равнобедренный. Р По теореме Чевы Если АА1 = ВВ1, то эта трапеция равнобокая, то есть АВ1 = А1В. Тогда по теореме Чевы В1С = А1С, а значит АС = АВ1 + В1С = А1С + А1В = ВС, то есть ∆АВС равнобедренный. 1.3 Вписанный угол. Теорема синусов Свойства угла, вписанного в окружность, подробно изучаются в школьном курсе геометрии. Тем не менее, эта конструкция достойна отдельного упоминания, так как из нее можно получить очень полезное доказательство теоремы синусов. Теорема о вписанном угле. Величина угла, вписанного в окружность, равна половине величины центрального угла, опирающегося на ту же дугу. Теорема синусов. В произвольном треугольнике отношения длин сторон треугольника к синусам противолежащих углов есть постоянная величина, равная диаметру описанной вокруг этого треугольника окружности. Упражнение 7. Докажите теорему синусов. (Указание: воспользуйтесь рисунком и выразите длину хорды (стороны треугольника) через радиус окружности и величину центрального угла.) Упражнение 8. Решите задачу. В треугольнике АВС Р Для сокращенной записи введем обозначение ∟АВС = β. Получаем ∟А В1С1 = β и ∟С В1А1 = β. Следовательно, ∟А1В1С1 = 2 β. По теореме синусов, радиус описанной окружности ∆ А1В1С1 равен
По условию, АС 2 =АВ 2 +ВС 2 -2АВ ·ВС· Ответ: 1.4 Окружность и касательная, окружность и секущая. Теоремы о свойствах секущихВспомогательная конструкция «окружность – секущая» часто встречается в разных задачах. Более того, она связана с важным понятием «степень точки относительно окружности». Мы рассмотрим только несколько конструкций, которые для удобства собраны на одном чертеже. Перечислим некоторые их свойства. Свойство 1. Длины отрезков касательных, проведенных к одной окружности из одной точки M равны ( MT 2 = MO 2 — R 2 ). Свойство 2. Произведения отрезков двух секущих к одной окружности равны ( MA MB = MC MD ). Свойство 3. Произведение отрезков внешней секущей равно квадрату отрезка касательной, проведенной из той же точки ( MA MB = MT 2 = MO 2 — R 2 ). Далее рассмотрим случай, когда точка расположена внутри окружности. Свойство 4. (аналог свойства 2) Произведения отрезков двух секущих к одной окружности равны ( MA MB = MC MD ). С Упражнения 9-13. Докажите свойства 1-5. Упражнение 14. Решите задачу. В окружности радиуса 17 проведена хорда АВ длины 30. Точка С лежит на хорде АВ так, что АС:ВС = 1:3. Найдите радиус окружности, касающейся данной окружности и касающейся хорды АВ в точке С. Решение. 1). Пусть О –центр данной окружности радиуса 17, а r – искомый радиус окружности, касающийся данной окружности и касающийся ее хорды АВ в точке С. Возможны лишь два случая расположения этой окружности: а) окружность и точка О лежат по одну сторону от хорды АВ. б) окружность и точка О лежат по разные стороны от хорды АВ. 2) Пусть точке Р – центр окружности, радиус которой мы ищем, а точка К – точка касания этой окружности с данной. Точка РК = СР = r , СР ┴ АВ. Т ак как точка касания двух окружностей принадлежит прямой, соединяющей их центры, то точки О, Р, К лежат на одной прямой. Поэтому ОК = ОР + РК, ОР = ОК – РК = 17 – r . Из треугольника СРО по теореме косинусов имеем: ОР 2 =СР 2 +СО 2 -2СР·СО· cos ∟ОСР 289 – 34r = CO 2 — 2r· СО ·cos∟ ОСР r = (289 – СО 2 ) : (34 — 2·СО· cos ∟ОСР) (*) ОМ 2 = ВО 2 — ВМ 2 = 17 2 -15 2 = 64 ⇒ СО 2 = СМ 2 + 64. Так как АС = 1/3ВС , то АС = 1/4 АВ = 15/2, СМ = АМ – АС = 15 – 15/2 = 15/2. Итак СО 2 = (15/2) 2 + 64 = 481/4. Поскольку ∟ОСР = 90 о — ∟ОСМ, то СО· cos ∟ОСР = СО· sin ∟ОСМ = ОМ = 8 Итак, r = (289 – 481/4) : (34 — 2·8) = 75/8 ∟ ОСР = r = (289 – СО 2 ) : (34 + 2·СО· cos ∟ОСР) = Ответ: 27/8 или 75/8 2. Основные конструкцииВ этой части мы рассмотрим основные конструкции, которые образуют треугольник и окружность. 2.1 Треугольник и описанная окружностьЦентр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. У остроугольного треугольника эта точка находится внутри, у прямоугольного – на середине гипотенузы, а у тупоугольного – вне треугольника. Упражнение 15. Докажите, что если два треугольника имеют общую сторону, то прямая, проходящая через центры описанных окружностей этих треугольников делит такую сторону пополам (проходит через середину стороны). Из теоремы о вписанном угле следует, что из центра описанной окружности каждая сторона видна под углом, в два раза большем, чем противолежащий угол треугольника. Используйте это свойство для решения следующего упражнения. Упражнение 16. Выразить стороны треугольника через его углы и радиус описанной окружности. Упражнение 17. Докажите для произвольного треугольника следующую формулу: 2.2 Частные случаи: прямоугольный, равнобедренный и равносторонний треугольникКак уже отмечалось выше, у прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы. Отсюда следует, что радиус описанной вокруг прямоугольного треугольника окружности равен половине его гипотенузы. Справедлива также следующая теорема. Теорема. Если радиус описанной окружности некоторого треугольника равен половине длины одной из его сторон, то этот треугольник – прямоугольный. Упражнение 18. Докажите теорему. (Указание: покажите, что центр описанной окружности лежит на середине стороны треугольника, и найдите синус противоположного угла с помощью теоремы синусов.)
Упражнение 19. Выразите отношение радиуса описанной окружности равнобедренного треугольника к его высоте через угол при вершине этого треугольника. Рассмотрим, наконец, равносторонний или правильный треугольник. В этом треугольнике высоты являются медианами, биссектрисами и серединными перпендикулярами. Поэтому центр описанной окружности совпадает с точкой пересечения медиан. Так как точка пересечения медиан делит каждую из них в отношении 2 к 1 считая от вершины, то радиус описанной окружности равен двум третьим от высоты. Таким образом, Упражнение 20. Выразите высоту, сторону и площадь равностороннего треугольника через радиус описанной окружности. 2.3 Треугольник и вписанная (вневписанная) окружность
Рассмотрим некоторые свойства вписанного треугольника. П Упражнение 21. Докажите, что отрезки, соединяющие вершины треугольника с точками касания вписанной окружности, лежащими на противоположных сторонах, пересекаются в одной точке. Упражнение 22. Решите задачу. В треугольнике АВС: АВ = 12, АС = 9, ВС = 6. На прямой ВС взята точка D так, что В D : D С = 1 :7. В треугольнике А D С и А D В вписаны окружности, касающиеся прямой А D в точках Е и F . Найдите длину отрезка EF . Решение. Так как BD CD , то возможны только два случая расположения точки D на прямой BC . а) Точка D лежит на отрезке ВС. б) Точка D лежит на продолжении стороны ВС за точку В. Из соотношения ВD : DС = 1 :7 имеем: В случае а) BD = 1/8 BC = 3/4, CD = 7 BD = 21/4. В случае б) BD = 1/7 DC , BC = 6/7 DC ⇒ BD = 1/6 BC = 1, CD = 7 BD = 7. Получаем DF = (AD+BD-AB)/2, DE = (AD+CD-AC)/2. Таким образом, EF = DE — DF , EF = ( CD – AC – BD + AB )/2. В случае а) EF = (21/4 – 9 — 3/4 + 12)/2 = 1/2·15/2 = 15/4 В случае б) EF = (7 – 9 – 1 + 12)/2 = 9/2 Ответ: 3,75 или 4,5. Если вписанные окружности всем хорошо знакомы, то вневписанными встречаются реже. Поясним, чем они отличаются от вписанных. Итак, центр вневписанной окружности лежит вне треугольника. Это точка пересечения биссектрис одного внутреннего и двух внешних углов треугольника. Вневписанная окружность касается одной стороны и продолжений двух других сторон треугольника. Для треугольника существует три вневписанных окружности. (На рисунке изображены вписанная и вневписанная окружности. Хорошо видно, что точки касания этих окружностей со стороной треугольника не совпадают.) Упражнение 23. Выразите длины отрезков касательных, проведенных из вершин треугольника к вневписанной окружности, через длины сторон этого треугольника. (Указание: используйте метод, который был применен к вписанной окружности.) Найдем выражения для радиусов вписанной и вневписанных окружностей. Начнем со случая вписанной окружности. « Разрежем» треугольник на три треугольника так, как показано на рисунке. Каждый из них имеет высоту, равную радиусу вписанной окружности. Сумма площадей трех треугольников равна площади большого: Отсюда легко получить формулу для вычисления радиуса вписанной окружности: Радиусы вневписанных окружностей можно получить аналогично. Представим площадь треугольника ABC так: Далее применим те же рассуждения, что и ранее. В результате получим следующую формулу: Упражнение 24. Докажите, что прямые, соединяющие вершины треугольника с точками касания сторон или продолжений сторон этого треугольника с вневписанной окружностью, пересекаются в одной точке. (Указание: используйте теорему Чевы.) 3 Задачи для самостоятельного решения. 1. Две окружности внешне касаются в точке А, ВС — их общая внешняя касательная. Доказать, что 2. Две окружности пересекаются в точках А и В. Точки А и В лежат по разные стороны от прямой l , которая пересекает окружности соответственно в точках С, D, Е и М. Доказать, что сумма углов DBE и САМ равна 180°. 3. Две окружности пересекаются в точках А и В. Прямые l 1 и l 2 параллельны, причем l 1 проходит через точку А и пересекает окружности в точках Е и К, а l 2 проходит через точку В и пересекает окружности в точках М и Р. Доказать, что четырехугольник ЕКМР — параллелограмм. 4. Из точки М проведены к окружности с центром в точке О касательные МА и МВ. Прямая l касается окружности в точке С и пересекает МА и МВ соответственно в точках D и Е. Доказать, что: а) периметр треугольника MDE не зависит от Выбора точки С; б) угол DOE не зависит от выбора точки С. 5. Точки А, В, С и D делят окружность на части, отношение которых 1 : 3 : 5 : 6. Найти углы между касательными к окружности, проведенными в точках А, В, С и D. 6. Две равные окружности внешне касаются друг друга и третьей окружности, радиус которой равен 8 см. Отрезок, соединяющий точки касания двух равных окружностей с третьей, равен 12 см. Найти радиусы равных окружностей. 7. Общая хорда двух пересекающихся окружностей равна а и служит для одной окружности стороной правильного вписанного шестиугольника: а для другой вписанного квадрата. Найти расстояние между центрами окружностей. 8. Две окружности радиусами, и R касаются внешним образом. Найти длину их общей внешней касательной. 9. Две окружности радиусами r и R касаются внешним образом. Прямая 1 пересекает окружности в точках А, В, С и D так, что АВ = ВС = CD. Найти AD. 10. Две окружности, радиусы которых относятся как 1 : 3, касаются внешним образом, длина их общей внешней касательной 11. Из внешней точки к окружности проведены секущая длиной 48 см и касательная, длина которой составляет 12. Общая внешняя касательная двух внешне касающихся окружностей составляет с линией центров угол а. Найти отношение радиусов. 13. Из точки А, расположенной вне круга с центром О, проведены секущие АВС и АМК (В и М — ближайшие к А точки окружности, лежащие на секущих). Найти ВС, если известно, что 14. Две окружности пересекаются в точках А и В. Через точку А проведены отрезки АС и AD, каждый из которых, являясь хордой одной окружности, касается другой окружности. Доказать, что АС 2 . BD = AD 2 . B С. 15. АВ и CD — взаимно перпендикулярные пересекающиеся хорды окружности радиуса R. Доказать, что АС 2 + BD 2 = 4R 2 . 16. Доказать, что сумма квадратов расстояний от точки М, взятой на диаметре окружности, до концов любой из параллельных этому диаметру хорд есть для данной окружности постоянная величина. 17. Две окружности внешне касаются в точке С, АВ — их общая внешняя касательная. Найти радиусы, если АС = 8 см, ВС = 6 см. 18. Окружности радиусами R и 19. Окружности радиусами а и b имеют внутреннее касание (а b ), причем центр большей окружности лежит вне меньшей окружности. Хорда АВ большей окружности касается меньшей окружности и образует с общей касательной к окружностям угол 20. В правильном треугольнике АВС на сторонах АВ и АС взяты точки М и К так, что АМ : МВ = 2 : 1, АК : КС = 1 : 2. Доказать, что отрезок КМ равен радиусу окружности, описанной около треугольника АВС. Список использованной литературы Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. 10-11 классы: учеб. Для общеобразоват. учреждений: базовый и профил. уровни– 18-е изд. – М.: Просвещение, 2009. – 255 с. Гусев В.А., Кожухов И.Б., Прокофьев А.А. Геометрия. Полный справочник. – М.: Махаон, 2006. – 320 с. Лаппо Л.Д., Филонов А.Н. Математика. Экспресс-курс подготовки к ЕГЭ: учебное пособие. – М.: Издательство «Экзамен», 2004. – 96с. Мальцев Д.А. Математика. Все для ЕГЭ 2011. Часть 1: учебно-методическое пособие. – Ростов н/Д: Издатель Мальцев Д.А.; М.: НИИ школьных технологий, 2010. – 221 с. Мельникова Н.Б. Геометрия: Дидакт. Метериалы для 10-11 кл. общеобразоват. Учреждений. – 2-е изд. –М.: Мнемозина, 1999. – 272 с. Полонский В.Б., Рабинович Е.М., Якир М.С. Учимся решать задачи по геометрии. Учеб.-метод. пособие. – К. «Магистр», 1996, – 256 стр. Потоскуев Е.В., Звавич. Л.И. Геометрия. 10 кл.: учеб. для общеобразоват. учреждений с углубл. и профильным изучением математики /– 3-е изд. – М.: Дрофа, 2005. – 223 с. Потоскуев Е.В., Звавич. Л.И. Геометрия. 11 кл.: учеб. для общеобразоват. учреждений с углубл. и профильным изучением математики – 3-е изд. – М.:Дрофа, 2003. – 368 с. Прасолов В.В. Задачи по планиметрии: Учебное пособие. – 5-е изд., испр. И доп. –М.: МЦНМО: ОАО «Московские учебники», 2006. – 640с. Прокофьев А.А. Пособие по геометрии для подготовительных курсов (планиметрия). – 4-е изд. перераб. и доп. – М.:МИЭТ, 2007, 232 стр. Шарыгин И.Ф. Геометрия. 10-11 классы: учеб. Для общеобразоват. заведений. – М.: Дрофа, 1999. – 208 с Шарыгин И.Ф. Сборник задач по геометрии. 5000 задач с ответами / И.Ф. | |















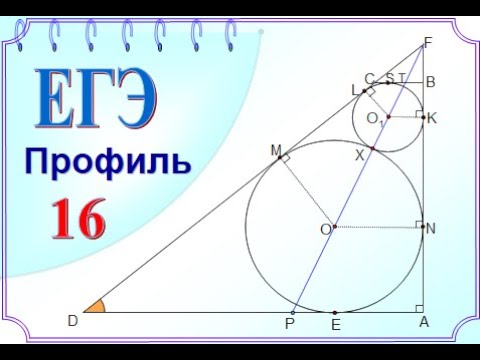















































 пересечен прямой, не параллельной стороне А C и пересекающей две его стороны А B и ВС соответственно в точках C 1 и А1, а прямую А C в точке B 1 тогда
пересечен прямой, не параллельной стороне А C и пересекающей две его стороны А B и ВС соответственно в точках C 1 и А1, а прямую А C в точке B 1 тогда (1)
(1) ,
, ешение
ешение

 . (2)
. (2) ешение.
ешение.





 , АВ =4, ВС =3, точки А 1 , В 1 , С 1 – основания высот треугольника АВС. Найдите радиус окружности, описанной вокруг треугольника А В 1 С 1.
, АВ =4, ВС =3, точки А 1 , В 1 , С 1 – основания высот треугольника АВС. Найдите радиус окружности, описанной вокруг треугольника А В 1 С 1.  ешение.
ешение. .
.
 , чтобы найти R, остается вычислить А 1 В 1 С 1 .
, чтобы найти R, остается вычислить А 1 В 1 С 1 .  Найдем АС по теореме косинусов:
Найдем АС по теореме косинусов: , АС 2 =4 2 +3 2 -2·4·3·
, АС 2 =4 2 +3 2 -2·4·3·  = 17, АС =
= 17, АС =  . Значит А 1 С 1 =
. Значит А 1 С 1 =  и окончательно получаем:
и окончательно получаем:





 90 о + ∟ОСМ, поэтому получаем
90 о + ∟ОСМ, поэтому получаем , здесь a , b и c – стороны, R – радиус описанной окружности, S – площадь треугольника. (Указание: используйте выражение для стороны c из предыдущего упражнения и формулу для площади треугольника
, здесь a , b и c – стороны, R – радиус описанной окружности, S – площадь треугольника. (Указание: используйте выражение для стороны c из предыдущего упражнения и формулу для площади треугольника  .)
.)

 , где a – сторона треугольника.
, где a – сторона треугольника.





 .
. .
. .
.
 .
. .
. см. Найти периметр фигуры, образованной внешними касательными и внешними дугами окружностей.
см. Найти периметр фигуры, образованной внешними касательными и внешними дугами окружностей. от внутреннего отрезка секущей. Найти радиус окружности, если известно, что секущая удалена от центра на расстояние 24 см.
от внутреннего отрезка секущей. Найти радиус окружности, если известно, что секущая удалена от центра на расстояние 24 см. и секущая АМК проходит через центр окружности.
и секущая АМК проходит через центр окружности. касаются внешним образом. Из центра меньшей окружности под углом 30° к линии центров проведен отрезок длиной 2R. Найти длины тех частей отрезка, которые лежат вне окружностей.
касаются внешним образом. Из центра меньшей окружности под углом 30° к линии центров проведен отрезок длиной 2R. Найти длины тех частей отрезка, которые лежат вне окружностей. . Найти АВ.
. Найти АВ.