Из центра окружности проведен к ее плоскости перпендикуляр

Геометрия | 5 — 9 классы

Из центра круга радиуса 9 см восстановлен перпендикуляр к его плоскости.

Найдите расстояние от конца этого перпендикуляра до точек окружности , если длинаперпендикуляра 40 см.

Расстояние от конца перпендикуляра до точек окружности есть гипотенуза прямоугольного треугольника образованного перпендикуляром и радиусом.

Пифагора с = √(9² + 40²) = √(81 + 1600) = 41 см.

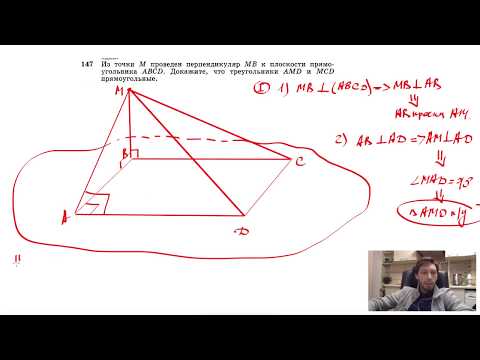
Видео:№147. Из точки М проведен перпендикуляр МВ к плоскости прямоугольника ABCD. Докажите, чтоСкачать

Из точки окружности радиуса 30 см проведен к радиусу перпендикуляр, который поделил радиус в соотношении 3 : 2(считая от центра)Вычислить длину хорды окружности, содержащей перпендикуляр к радиусу?

Из точки окружности радиуса 30 см проведен к радиусу перпендикуляр, который поделил радиус в соотношении 3 : 2(считая от центра)Вычислить длину хорды окружности, содержащей перпендикуляр к радиусу.

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Стороны треугольника 10, 17, 21 см?

Стороны треугольника 10, 17, 21 см.

Из вершины наибольшего угла восстановлен перпендикуляр к плоскости треугольника.

Длина этого перепендикуляра 15 см.

Найдите расстояние от конца( не лежащего на плоскости) перпендикуляра до наибольшей стороны треугольника.

Видео:№140. Из точки А, не принадлежащей плоскости α, проведены к этой плоскости перпендикуляр АОСкачать

Из центра круга радиуса 5 см восставлен перпендикуляр к его плоскости?

Из центра круга радиуса 5 см восставлен перпендикуляр к его плоскости.

Найдите длину этого перпендикуляра , если расстояние от конца перпендикуляра доточекокружности равно 13 см.

Видео:Геометрия 10 класс (Урок№10 - Перпендикуляр и наклонные.)Скачать

Точки А и В, лежащие в перпендикулярных плоскостях, соединенные отрезком длиной d?

Точки А и В, лежащие в перпендикулярных плоскостях, соединенные отрезком длиной d.

Перпендикуляры проведены из этих точек до линии пересечения плоскостей, равны а и b.

Найдите расстояние между основаниями этих перпендикуляров.

Видео:Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

8) Из центра равностороннего треугольника со стороной 0, 126 м восставлен перпендикуляр к плоскости этого треугольника?

8) Из центра равностороннего треугольника со стороной 0, 126 м восставлен перпендикуляр к плоскости этого треугольника.

Найдите расстояние от вершины перпендикуляра до сторон треугольника.

Видео:№138. Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которымиСкачать

Из центра круга, площадь которого 200, 96 см2 , проведен к его плоскости перпендикуляр, длина которого 12 см ?

Из центра круга, площадь которого 200, 96 см2 , проведен к его плоскости перпендикуляр, длина которого 12 см .

Найти расстояние от конца этого перпендикуляра до точек окружности.

Видео:Стереометрия "с нуля" Урок 6 Перпендикуляр и наклонная к плоскостиСкачать

Стороны равнобедренного треугольника равны 17, 17 и 30 см?

Стороны равнобедренного треугольника равны 17, 17 и 30 см.

Из вершины большого угла восстановлен перпендикуляр к плоскости треугольника.

Его длина 15 см.

Найдите расстояние от концов этого перпендикуляра до большей стороны треугольника.

Видео:10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Стороны прямоугольника равны 9 и 12 см?

Стороны прямоугольника равны 9 и 12 см.

Из середины большей стороны восстановлен перпендикуляр длиной 4, 8см к плоскости прямоугольника.

Найти расстояние от конца этого перпендикуляра до одной из диагоналей.

Приложите , пожалуйста, рисунок для решения.

Видео:Наклонная, проекция, перпендикуляр. 7 класс.Скачать

Длины катетов прямоугольного треугольника равны 9 см и 16 см?

Длины катетов прямоугольного треугольника равны 9 см и 16 см.

К плоскости треугольника из середины гипотенузы восстановлен перпендикуляр, длина которого равна 12 см.

Вычислите расстояния от свободного конца перпендикуляр до катетов.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

В плоскости М описана окружность, длина которой равна с?

В плоскости М описана окружность, длина которой равна с.

Из центра О окружности восстановлен к плоскости перпендикуляр ОА = h.

Найти угол между этим перпендикуляром и прямой, соединяющей его конец А с произвольной точкой N окружности.

На странице вопроса Из центра круга радиуса 9 см восстановлен перпендикуляр к его плоскости? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

1) Р(периметр) трапеции. = 2АВ + ВС + АД = 2АВ + 5 + АД = 23 ; = > АД = 23 — 5 — 2АВ = 18 — 2АВ. 2) Т. К. АС — бис — са угла А, то углы ВАС и САД равны. Но углы ВСА и САД равны как внутренние накрест лежащие при ВСIIАД и секущей АС. Тогда углы В..

За т. Синусов можно a / sina = b / sinb = c / sinc a / sina = c / sinc 8 / 0. 8 = x / 1 0. 8x = 8 x = 10 Ответ : АВ = 10.

Изобразите на рисунке взаимное расположение точек А, В и С, если а)АС = 3АВ A_. _. _. _. _B_. _. _. _. _. _. _. _. _. _C б)АВ = — 3АС ; C_. _. _. _. _A_. _. _. _. _. _. _. _. _. _. _. _. _. _. _B в)АС = 1 / 3АВ А_. _. _. _. _С_. _.

6. Треугольники АВС и ВСД равны по : 1. Угол 1 = углу 4 (по условию), 2. Угол 2 = углу 3 (по условию), 3. Сторона ВД — общая Ответ : треугольники равны по первому признаку.

S = AB * AC * sin A sin 45 = корень2 / 2 S = 6. 5 * 6корень2 * корень2 / 2 = 78 / 2 = 39.

Общая хорда двух пересекающихся окружностей видна из их центров под углами 90° и 60°. Найти радиус большей окружности, если центры окружностей лежат по разные стороны от хорды, а расстояние между центрами равно 0, 25(1 + √3). ————— Обозначим центр ..

(по усл. ) — это «по условию» (по Th о пар. Пр. ) — это «по теореме о параллельности прямых» (по смете. Угл. ) — это «по смежным углам».

Описанная окружность (центр расположили на оси OX) ; в полярных координатах Прямая x = d пересекает окружность в точках A и B (|AB| = c известно, ). Луч, выходящий из начала координат и образующий угол с осью OX, пересекает AB в точке D : а окружн..

Так, вторая попытка : ) Постараюсь коротко. 1) Окружность заданного радиуса R. 2) в ней хорда заданной длины AB. 3) диаметр DF через середину AB — точку M ; обозначу DM = d ; 4) на MF, как на диаметре, строится окружность. O1 — её центр 5) DK — к..

(180° — 130°) : 2 = 25° Его углы : 130°, 25°, 25°.

Видео:Построение окружности по трём точкам.Скачать

Одной линейкой

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Задача

Даны окружность с центром О и точка А вне окружности. а) Проведен диаметр окружности. Пользуясь только линейкой*, опустите перпендикуляр из точки А на этот диаметр. б) Через точку А проведена прямая, не имеющая общих точек с окружностью. Пользуясь только линейкой, опустите перпендикуляр из точки О на эту прямую.

*Примечание. Под «линейкой» в задачах на построение всегда подразумевается не измерительный инструмент, а геометрический — с его помощью можно только проводить прямые (через две имеющиеся точки), но не измерять расстояние между точками. Кроме того, геометрическая линейка считается односторонней — с ее помощью нельзя провести параллельную прямую, просто приложив одну сторону линейки к двум точкам и проведя линию вдоль другой стороны.

Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Подсказка 1

Используйте концы диаметра, а не центр окружности.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Подсказка 2

Угол с вершиной на окружности, опирающийся на ее диаметр, — прямой. Зная это, вы можете построить две высоты в треугольнике, образованном концами диаметра и точкой А.

Видео:Геометрия 10 класс Атанасян №138 Как найти наклонную и проекцию если известен перпендикуляр и уголСкачать

Подсказка 3

Попробуйте решить сначала более простой случай, чем заданный в пункте б), — когда данная прямая пересекает окружность.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Решение

а) Пусть ВС — данный диаметр (рис. 1). Для решения задачи просто вспомним первые две подсказки: если провести прямые AВ и АC, а затем соединить точки их пересечения с окружностью с нужными вершинами треугольника ABC, то получатся две высоты этого треугольника. А так как высоты треугольника пересекаются в одной точке, то прямая CH будет третьей высотой, то есть искомым перпендикуляром из А к диаметру ВС.

б) Решение этого пункта, однако, даже в том случае, который дан в третьей подсказке, не кажется более простым: да, мы можем провести диаметры, соединить их концы и получить прямоугольник ABCD (рис. 2, на котором, для простоты, точка А отмечена на окружности), но как это приближает нас к построению перпендикуляра из центра окружности?

А вот как: так как треугольник AOB равнобедренный, то перпендикуляр (высота) OK пройдет через середину K стороны AB. А значит, задача свелась к нахождению середины этой стороны. Как ни удивительно, но окружность больше нам совсем не нужна, да и точка D тоже, в общем, «лишняя». А вот отрезок CD — не лишний, но на нем нам потребуется не какая-то конкретная точка, а совершенно произвольная точка E! Если обозначить за L точку пересечения BE и AC (рис. 3), а затем продлить AE до пересечения с продолжением BC в точке M, то прямая LM — это решение всех наших забот и проблем!

Правда, очень похоже, что LM пересекает AB посередине? Это и правда так. Попробуйте доказать это. Мы же отложим доказательство до конца решения задачи.

Итак, мы научились находить середину отрезка AB, а значит, научились опускать перпендикуляр на AB из центра окружности. Но что делать с исходной задачей, в которой данная прямая не пересекает окружность, как на рис. 4?

Постараемся свести задачу к уже решенной. Это можно сделать, например, так.

Сначала построим прямую, симметричную данной относительно центра окружности. Построение понятно из рис. 5, на котором данная прямая — горизонтальная под окружностью, а построенная симметричная ей — выделена красным (две синие точки могут быть взяты на окружности совершенно произвольно). Заодно проведем через центр О еще одну прямую, перпендикулярную к одной из сторон получившегося в окружности прямоугольника, чтобы получить на данной прямой два равных по длине отрезка.

Имея две параллельные прямые, на одной из которых уже отмечены два конца и середина отрезка, возьмем произвольную точку T (например, на окружности) и построим такую точку S, что прямая TS будет параллельна имеющимся двум прямым. Это построение показано на рис. 6.

Тем самым мы получили хорду окружности, параллельную данной прямой, то есть свели задачу к решенной ранее версии, ведь к такой хорде проводить перпендикуляр из центра окружности мы уже умеем.

Осталось привести доказательство факта, который мы использовали выше.

Четырехугольник ABCE на рис. 3 — трапеция, L — точка пересечения ее диагоналей, а M — точка пересечения продолжений ее боковых сторон. По известному свойству трапеции (его еще называют замечательным свойством трапеции; здесь можно посмотреть, как оно доказывается) прямая ML проходит через середины оснований трапеции.

Собственно, еще раз мы фактически опирались на эту же теорему уже в последней подзадаче, когда проводили третью параллельную прямую.

Видео:ОГЭ. Математика. Задание 26 | Перпендикуляр в окружности | Борис Трушин |Скачать

Послесловие

Теория геометрических построений одной линейкой, когда задана вспомогательная окружность с центром, разработана замечательным немецким геометром XIX века Якобом Штейнером (правильнее произносить его фамилию Steiner как «Штайнер», но в отечественной литературе уже давно закрепилось написание с двумя «е»). О его математических достижениях мы уже однажды рассказывали в задаче «Короче, Склифосовский». В книге «Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга» Штейнер доказал теорему, согласно которой любое построение, которое может быть выполнено с помощью циркуля и линейки, может быть выполнено и без циркуля, если задана всего одна окружность и отмечен ее центр. Доказательство Штейнера сводится к демонстрации возможности осуществления базовых построений, обычно выполняемых с помощью циркуля, — в частности, к проведению параллельных и перпендикулярных прямых. Наша задача, как легко видеть, является частным случаем этой демонстрации.

Впрочем, к некоторым задачам Штейнер привел не единственный способ решения. Приведем второй способ и мы.

Возьмем на данной прямой две произвольные точки A и B (рис. 7). Сначала строим перпендикуляр из A на (синюю) прямую BO — это фактически решение нашей первой задачи, потому что эта прямая содержит диаметр окружности; все соответствующие построения на рис. 7 выполнены синим цветом. Затем строим перпендикуляр из B на (зеленую) прямую AO — это точно такое же решение точно такой же задачи, построения выполнены зеленым цветом. Тем самым мы получили две высоты треугольника AOB. Третья высота этого треугольника проходит через центр O и точку пересечения двух других высот. Она и является искомым перпендикуляром к прямой AB.

Но и это еще не все. Несмотря на всю (относительную) простоту второго способа, он «избыточно длинный». Это означает, что существует другой способ построения, требующий меньшего числа операций (в задачах на построение каждая линия, проведенная циркулем или линейкой, считается как одна операция). Построения, требующие минимального среди известных количества операций, французский математик Эмиль Лемуан (Émile Lemoine, 1840–1912) назвал геометрографическими (см.: Geometrography).

Итак, вашему вниманию предлагается геометрографическое решение пункта б). Оно требует всего 10 шагов, при этом шесть первых — «естественные», а следующие три — «удивительные». Самый последний шаг, проведение перпендикуляра, пожалуй, тоже следует назвать естественным.

Мы хотим провести красный пунктирный перпендикуляр (рис. 8), для этого нам нужно отыскать на нем какую-нибудь точку, отличную от О. Поехали.

1) Пусть A — произвольная точка на прямой, а C — произвольная точка на окружности. Проводим прямую AC.

2)–3) Проводим диаметр OC (вторично пересекающий окружность в точке D) и прямую AD. Отмечаем вторые точки пересечения прямых AC и AD с окружностью — B и E, соответственно.

4)–6) Проводим BE, BD и CE. Прямые CD и BE пересеклись в точке H, а BD и CE — в точке G (рис. 9).

Кстати, а могло ли случиться так, что BE оказалось бы параллельно CD? Да, безусловно. В случае, когда диаметр CD перпендикулярен AO, то именно так и случается: BE и CD параллельны, а точки A, O и G лежат на одной прямой. Но возможность брать точку C произвольно предполагает наше умение выбрать ее так, чтобы CO и AO не были перпендикулярны!

И вот теперь обещанные удивительные шаги построения:

7) Проводим GH до пересечения с данной прямой в точке I.
8) Проводим CI до пересечения с окружностью в точке J.
9) Проводим BJ, которая пересекается с GH. где? Правильно, в красной точке, которая находится на вертикальном диаметре окружности (рис. 10).

10) Проводим вертикальный диаметр.

Вместо шага 8 можно было бы провести прямую DI, а затем на шаге 9 соединить вторую точку ее пересечения с окружностью с точкой E. Результат был бы той же самой красной точкой. Правда, это удивительно? Причем, даже неясно, что удивляет сильнее — то, что красная точка оказывается одной и той же для двух способов построения, или то, что она лежит на искомом перпендикуляре. Впрочем, геометрия — это ведь не «искусство факта», а «искусство доказательства». Так что постарайтесь доказать это.

Мелкая придирка не по существу:
> правильнее произносить его фамилию Steiner как «Штайнер», но в
> отечественной литературе уже давно закрепилось написание с двумя «е»

— ничего подобного. Так принято передавать немецкое -ei- для всех персон примерно до середины XX века. Причины этого не вполне понятны: фонетический переход -ei- в [-ai-] произошел за много веков до появления этой традиции транскрипции на русский
(в отличие, например, от перехода -ille- из [iλ] в [ij]: Марсель, Гильом — который произошел лишь в XIX веке, когда русская транскрипция уже устоялась).

Но по какой бы причине русская транскрипция с немецкого ни оказалась отстающей от реальной фонетики на много веков, она именно такова. Передавать Штейнера и прочих немцев XIX века через -ай- было бы анахронизмом. Не говоря уже о том, что Штейнер, помимо немецкой, еще и распространенная в России и других странах идишская фамилия, а их принято передавать через -ей- и по сей день.

А по существу вопрос: теорема гласит, что «любое построение, которое может быть выполнено с помощью циркуля и линейки, может быть выполнено и без циркуля, если задана всего одна окружность и отмечен ее центр».

Что имеется в виду под «если задана всего одна окружность»? Имеется ли в виду, что в задаче дана только одна окружность, и задание центра позволяет построить линейкой все то, что можно построить циркулем? Или имеется в виду, что берем любую задачу (скажем, деление отрезка пополам), и достаточно где-нибудь в произвольном месте задать окружность и ее центр, чтобы задача деления отрезка пополам решалась одной линейкой?

Да, имеется в виду ровно это. На плоскости чертежа задана произвольная окружность и ее центр. Это позволяет выполнить одной линейкой всё, что можно сделать циркулем и линейкой.

А деление отрезка пополам и так решается одной линейкой (без вспомогательной окружности). Вот одним циркулем — не решается.

> А деление отрезка пополам и так решается одной линейкой (без вспомогательной окружности

Допускаю, хотя не знаю такого способа.

> Вот одним циркулем — не решается.

Этого не может быть. По теореме Мора-Маскерони.

Этого противоречит вашим словам, будто линейкой можно построить середину отрезка.

Вот смотрите: если мы можем одной линейкой построить касательную к окружности из точки A, значит, возьмем две такие касательные. Проведем хорду, опирающуюся на две точки касания.

По вашим словам (выше), одной линейкой можно найти середину отрезка, а значит, и этой хорды.

Из исходной точки A через середину хорды проведем прямую. Это будет (продолженный) диаметр окружности.

Возьмем произвольную точку B и повторим с ней и той же окружностью то же самое. Получим второй диаметр.

Два диаметра дают нам центр окружности.

Итого получается, что если, как вы утверждаете, одной линейкой можно построить и касательную из заданной точки к заданной окружности, и середину заданного отрезка, то одной линейкой можно построить и центр данной окружности. Однако хорошо известно (доказано, по-моему, тем же Штейнером через сечения наклонного конуса), что это невозможно. А если б было возможно, то рассказанная вами теорема Штейнера-Понселе не имела бы смысла: получается, любое построение циркулем и линейкой можно было бы совершить просто линейкой безо всяких дополнительных условий (или точнее, требовалось бы иметь где-то окружность не обязательно с отмеченным центром).

Касательную одной линейкой точно можно построить, и это ничему не противоречит.

Что касается утверждения о построении середины отрезка, я хотел сказать вот что: для этого не нужно иметь вспомогательную окружность, достаточно иметь вспомогательную параллельную прямую.

Да, это тоже исследовано Штейнером. Он рассмотрел списки задач, разрешимых линейкой при следующих дополнительных условиях
а) дана одна параллельная прямая или отрезок, разделенный в известном рациональном отношении
б) даны две пары параллельных прямых, или два отрезка, деленные в рац. отношениях, или одна пара параллельных и один такой отрезок
в) дан вспомогательный квадрат

Все эти условия позволяют решать линейкой какой-то класс задач на построение, причем а) Ответить

Тогда и задача немного другая, и решение другое. Фактически в вашей задаче требуется построить квадрат по заданным противоположным вершинам (B и C).

PS. Насчет касательных. Да, конечно, построение не очень короткое — в сумме явно больше 15 линий получится. Через точку пересечения высот — экономнее

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Из центра окружности проведен к ее плоскости перпендикуляр

19.1. Определения шара, сферы и их элементов

С шаром и сферой мы уже знакомы. Напомним их определения.

Определение. Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не большем данного R ( R > 0). Данная точка называется центром шара, а данное расстояние R — радиусом шара .

Определение. Сферой называется множество всех точек пространства, находящихся от данной точки на расстоянии, равном данному R. Данные точка и расстояние R называются соответственно центром и радиусом сферы.

На рисунке 193 изображён шар с центром О и радиусом R = OА.

Из определений шара и сферы следует, что шар с центром О и радиусом R является объединением двух множеств точек: 1) множества точек M пространства, для которых OM (они называются внутренними точками шара и образуют его внутренность); 2) множества всех М, для которых ОМ = R (эти точки являются граничными точками шара, а их объединение составляет границу шара, которая называется шаровой поверхностью и является сферой c центром О и радиусом R ) .

Радиусом шара называют также всякий отрезок, соединяющий центр шара с точкой шаровой поверхности. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара . Концы любого диаметра шара называются диаметрально nротивоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара ( сферы ) . На рисунке 193 отрезки ОА, ОВ, ON, OS — радиусы шара; отрезки АВ , NS — диаметры шара; A и B — диаметрально противоположные точки шара. Из определения диаметра шара следует, что он равен удвоенному радиусу шара.

Покажем, что шар — тело вращения. Для этого рассмотрим полукруг F с центром О и радиусом R (рис. 194, а ). При вращении полукруга F вокруг прямой, содержащей его диаметр NS, образуется некоторое тело F 1 (рис. 194, б ). Так как вращение вокруг прямой — движение и точка О принадлежит оси l вращения, то каждая точка тела F 1 удалена от точки O на расстояние, не большее R (движение сохраняет расстояния между точками). Это означает, что тело F 1 есть шар с центром О и радиусом R. Кроме того, при вращении границы полукруга — полуокружности — вокруг прямой l образуется сфера. Прямая, содержащая любой диаметр шара, может быть рассмотрена как ось вращения. Следовательно, сечением шара плоскостью, перпендикулярной его оси вращения l и пересекающей шар, является круг, а сечением сферы такой плоскостью — окружность этого круга; центр круга (окружности) есть точка пересечения секущей плоскости с осью l.

Плоскость, проходящая через центр шара (сферы), называется диаметральной плоскостью шара ( сферы ) . Сечением шара диаметральной плоскостью является круг, радиус которого равен радиусу шара. Такой круг называется большим кругом, а его окружность — большой окружностью ; большая окружность является пересечением сферы и её диаметральной плоскости.

19.2. Изображение сферы

Рассмотрим сферу, диаметр NS которой проведён вертикально (рис. 195, а ). Большая окружность, по которой сферу пересекает диаметральная плоскость, перпендикулярная диаметру (оси) NS, называется экватором , а точки N и S — полюсами сферы . Окружность, ограничивающая круг — изображение сферы, — называется абрисом или очерковой линией .

Типичная ошибка (!) при изображении сферы (рис. 195, б ) в том, что, изображая её экватор эллипсом, полюсы изображают расположенными на абрисе.

Для верного и наглядного изображения сферы вспомним, как в курсе черчения изображают фигуру на комплексном двухкартинном чертеже (эпюре) посредством ортогонального её проектирования на две взаимно перпендикулярные плоскости, одну из которых называют фронтальной (обозначают V ) , а другую — профильной (обозначают W ) плоскостями проекций.

Сферу расположим так, чтобы её ось N ′ S ′ была параллельна профильной ( W ), но не параллельна фронтальной ( V ) плоскостям проекций. Тогда ортогональные проекции сферы на плоскости V и W имеют вид, изображённый на рисунке 196. На нём: равные круги — проекции сферы на плоскости V и W ; отрезки A 1 B 1 и N 1 S 1 — профильные проекции соответственно экватора и оси сферы; точки N, S — фронтальные проекции полюсов (строятся с помощью линий связи); точки А, В — фронтальные проекции концов диаметра экватора, параллельного фронтальной плоскости (строятся с помощью линий связи); отрезок CD — фронтальная проекция диаметра C ′ D ′ сферы, перпендикулярного профильной плоскости; эллипс с осями АВ и CD — фронтальная проекция экватора. При таком расположении относительно плоскостей проекций сфера изображается так, как показано на рисунках 195, a ; 196, a.

Обратите внимание! Полюсы N и S не лежат на абрисе, и экватор изображается эллипсом. При этом положение полюсов N и S и положение вершин А и В эллипса-экватора взаимосвязаны.

Действительно, из равенства △ ОBF = △ ЕNО (см. рис. 196, а ) следует: OВ = EN, BF = NO. Это означает: а) если изображены полюсы N и S сферы, то вершины А и В эллипса — изображения экватора определяются из равенств OВ = ОА = NE, где NE || OD ; б) если изображён экватор (т. е. дана малая ось AB эллипса-экватора), то положение полюсов N и S определяется из равенств ON = OS = BF, где BF || OD.

На рисунке 197, а — верное и наглядное изображение сферы, на рисунке 197, б — изображение сферы верное (почему?), но не наглядное; на рисунке 197, в — неверное изображение (почему?).

 ЗАДАЧА (3.106). Найти в пространстве множество вершин всех прямых углов, опирающихся на данный отрезок АВ.

Решени е. Если ∠ АМВ = 90 ° , то точка М принадлежит окружности с диаметром АВ (рис. 198, a ).

Проведём произвольную плоскость α , содержащую отрезок АВ. В этой плоскости множество всех точек М, из которых отрезок AB виден под прямым углом, есть окружность, для которой отрезок AB — диаметр. Точки А и В этому множеству точек не принадлежат. (Почему?) Таким образом, искомое множество вершин прямых углов, опирающихся на отрезок AB , есть сфера с диаметром AB . Точки А и В этому множеству точек-вершин не принадлежат.

19.3. Уравнение сферы

Составим уравнение сферы с центром А ( a ; b ; с ) и радиусом R в декартовой прямоугольной системе координат Oxyz.

Пусть М ( x ; у ; z ) — любая точка этой сферы (рис. 199). Тогда MA = R или MA 2 = R 2 . Учитывая, что MA 2 = ( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 , получаем искомое уравнение cферы

( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 = R 2 .

Если начало системы координат совпадает с центром A сферы, то a = b = c = 0 , а сфера в такой системе координат имеет уравнение

x 2 + y 2 + z 2 = R 2 .

Из полученных уравнений следует, что сфера — поверхность второго порядка.

Так как для любой точки М ( х ; у ; z ) шара с центром А ( a ; b ; с ) и радиусом R выполняется МА ⩽ R, то этот шар может быть задан неравенством

( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 ⩽ R 2 .

При этом для всех внутренних точек М шара выполняется условие МА 2 R 2 , т. е.

( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 R 2 ,

для точек М шаровой поверхности — условие

т. е. ( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 = R 2 ,

для точек М вне шара — условие

т. е. ( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 > R 2 .

19.4. Пересечение шара и сферы с плоскостью

Рассмотрим подробнее вопрос о пересечении шара и сферы с плоскостью. Имеет место следующая теорема.

Теорема 30 (о пересечении шара и сферы с плоскостью ) . 1) Если расстояние от центра шара до данной плоскости меньше радиуса шара, то пересечением шара с плоскостью является круг. Центром этого круга является основание перпендикуляра, проведённого из центра шара на плоскость, или сам центр шара, если плоскость проходит через этот центр. Пересечением сферы с плоскостью является окружность указанного круга. Радиус r сечения в этом случае равен r = , где R — радиус шара, a d — расстояние от центра шара до плоскости сечения. 2) Если расстояние от центра шара до данной плоскости равно радиусу шара, то плоскость имеет с шаром и ограничивающей его сферой только одну общую точку. 3) Если расстояние от центра шара до данной плоскости больше радиуса, то плоскость не имеет с шаром общих точек.

Доказательств о. Пусть точка О — центр шара, R — его радиус; α — данная плоскость, точка A — основание перпендикуляра, проведённого из центра O на плоскость α . Обозначим ρ ( О ; α ) = | ОА | = d — расстояние от центра шара до плоскости α .

Рассмотрим каждый из случаев взаимного расположения шара и данной плоскости α .

1) ρ ( O ; α ) = d R и плоскость α не проходит через центр О шара (рис. 200). Докажем, что пересечение шара и плоскости есть круг с центром А и радиусом r = . Для этого достаточно убедиться, что любая точка пересечения шара и плоскости α есть точка круга с центром А и радиусом r = и, обратно, любая точка этого круга есть точка указанного пересечения.

Действительно, пусть М — произвольная точка шара, принадлежащая плоскости α (см. рис. 200). В прямоугольном треугольнике AOM по теореме Пифагора ОM 2 = ОА 2 + АМ 2 , откуда AM = . Так как точка М принадлежит шару, то ОМ ⩽ R, тогда OM 2 – OA 2 ⩽ R 2 – d 2 , поэтому АМ ⩽ . Это означает, что точка М сечения шара плоскостью α находится от точки А на расстоянии, не большем , следовательно, она принадлежит кругу с центром А и радиусом .

Обратно, пусть М — произвольная точка плоскости α , принадлежащая кругу с центром А и радиусом r = . В прямоугольном треугольнике AOM по теореме Пифагора OM 2 = ОA 2 + AM 2 . Так как AM ⩽ r , то OM 2 ⩽ OA 2 + r 2 = d 2 + R 2 – d 2 = R 2 , откуда OM ⩽ R . Значит, точка М принадлежит данному шару. Учитывая, что точка М принадлежит и плоскости α , приходим к выводу: точка M принадлежит пересечению данного шара и плоскости α .

Если неравенства, которые использовались в предыдущем доказательстве, заменить равенствами, то, рассуждая аналогично, можно доказать, что при d R пересечением сферы и плоскости является окружность с центром А и радиусом r = . Проделайте это самостоятельно.

Если плоскость α проходит через центр O шара, то d = 0, значит, r = R, т. е. сечением шара такой плоскостью является большой круг, а сечением сферы — большая окружность (см. рис. 200).

2) ρ ( O ; α ) = d = OA = R (рис. 201).

Так как ОА = ρ ( O ; α ) = R, то точка А, являющаяся основанием перпендикуляра из центра О шара на плоскость α , принадлежит шаровой поверхности, ограничивающей данный шар.

Пусть M — произвольная точка плоскости α , отличная от точки A (см. рис. 201). Тогда длины наклонной ОМ и перпендикуляра OA, проведённых из точки О к плоскости α , удовлетворяют неравенству OM > ОА = R. Значит, точка М не принадлежит шару. Следовательно, плоскость α имеет только одну общую точку с шаром — точку А.

3) ρ ( О ; α ) = ОА = d > R (рис. 202). Для любой точки М плоскости α выполняется (почему?) ОМ ⩾ d > R. Это означает, что на плоскости α нет точек шара. Теорема доказана. ▼

 ЗАДАЧА (3.161). Через середину радиуса шара проведена перпендикулярная к нему плоскость. Радиус шара равен R. Найти: а) площадь получившегося сечения; б) площади боковой и полной поверхностей конуса, основанием которого служит получившееся сечение шара, а вершиной — центр шара; в) площади боковой и полной поверхностей правильной треугольной пирамиды, вписанной в этот конус.

Решени е. а) Пусть точка O — центр шара, OD — его радиус, точка С — середина радиуса OD ; α — секущая плоскость, проходящая через точку С перпендикулярно OD.

Рассмотрим сечение шара диаметральной плоскостью, проходящей через его радиус OD. Этим сечением является большой круг с центром О и радиусом R (рис. 203); АВ — диаметр круга — сечения данного шара плоскостью α .

Так как АВ ⟂ OD и точка С — середина радиуса OD, то отрезок AB равен стороне правильного треугольника, вписанного в окружность радиуса R, значит, АВ = R , откуда

АС = r = , где r — радиус сечения шара плоскостью α . Тогда площадь этого сечения равна π r 2 = .

б) Найдём площадь поверхности конуса с вершиной О и радиусом основания r = .

Образующая ОЕ конуса (рис. 204) равна радиусу R данного шара. Поэтому площадь боковой поверхности этого конуса равна

π r • R = π • • R = ,

а площадь его полной поверхности — + = π R 2 • (2 + ).

в) Найдём площадь поверхности правильной треугольной пирамиды OEFK, вписанной в конус, радиус основания которого СK = r = , боковое ребро OE пирамиды равно радиусу R данного шара (см. рис. 204).

Так как △ ЕFK — правильный, вписанный в окружность радиуса r = , то сторона этого треугольника равна r , т. е. EF = . Тогда S △ EFK = = .

Площадь боковой поверхности пирамиды равна 3 S △ EOF = EF • ОН, где OH — апофема пирамиды. В прямоугольном треугольнике OHF находим

ОН = = = .

Тогда EF • OH = — площадь боковой поверхности пирамиды.

Следовательно, площадь полной поверхности пирамиды равна

+ = R 2 ( + ).

Ответ: a) ; б) π R 2 (2 + ); в) ; R 2 ( + ).

19.5. Плоскость, касательная к сфере и шару

Из теоремы 30 следует, что плоскость может иметь со сферой (с шаром) только одну общую точку.

Определение. Плоскость, имеющая только одну общую точку со сферой (с шаром), называется касательной плоскостью к сфере (шару), а их единственная общая точка называется точкой касания (рис. 205).

Также говорят, что плоскость касается сферы (шара) .

Любая прямая, лежащая в касательной плоскости к сфере и проходящая через точку их касания, называется касательной прямой к сфере ; эта прямая имеет со сферой единственную общую точку — точку касания, и радиус сферы, проведённый в точку касания, перпендикулярен касательной прямой.

Заметим, что если прямая a касается сферы в точке М , то эта прямая касается в точке М той окружности большого круга, которая является сечением сферы и диаметральной плоскости, проходящей через прямую a.

Справедливо и обратное: если прямая a касается окружности большого круга сферы в точке М , то эта прямая касается в точке М самой сферы.

Более того, так как прямая a, касающаяся сферы в точке М , имеет со сферой лишь одну общую точку — точку М , то эта прямая касается любой окружности, по которой пересекаются данная сфера и любая (не только диаметральная) плоскость, проходящая через прямую a. А поскольку радиус, проведённый в точку касания прямой и окружности, перпендикулярен касательной прямой, то центры всех этих окружностей — полученных сечений сферы — лежат в плоскости, проходящей через точку М перпендикулярно касательной прямой a. При этом, если точка О — центр данной сферы радиуса R , точка А — центр окружности радиуса r , по которой пересекает сферу одна (любая) из плоскостей, проходящих через касательную в точке М прямую к данной сфере, ϕ — величина угла между этой секущей плоскостью и проходящей через точку М диаметральной плоскостью данной сферы, то справедливо равенство r = R • cos ϕ ( △ ОАМ — прямоугольный, так как отрезок ОА перпендикулярен секущей плоскости (почему?)).

Для плоскости, касательной к сфере, справедливы теоремы, аналогичные теоремам о прямой, касательной к окружности на плоскости.

Теорема 31. Если плоскость касается сферы, то она перпендикулярна радиусу, проведённому в точку касания.

Доказательств о. Пусть дана сфера с центром O и радиусом R. Рассмотрим плоскость α , касающуюся данной сферы в точке M (см. рис. 205) и докажем, что ОM ⟂ α .

Предположим, что радиус ОM — не перпендикуляр, а наклонная к плоскости α . Значит, расстояние от центра сферы до плоскости α , равное длине перпендикуляра, проведённого из центра О на плоскость α , меньше радиуса. Тогда по теореме 30 плоскость α пересекает сферу по окружности. Но по условию теоремы плоскость α касается сферы и имеет с ней единственную общую точку M. Пришли к противоречию, которое и доказывает, что OM ⟂ α . Теорема доказана. ▼

Справедлива обратная теорема.

Теорема 32. Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведённому в эту точку, то она касается сферы.

Доказательств о. Пусть плоскость α проходит через точку M сферы и перпендикулярна радиусу ОM (см. рис. 205). Значит, расстояние от центра сферы до плоскости равно радиусу ОM. Тогда по теореме 30 плоскость α и сфера имеют единственную общую точку M, следовательно, плоскость α касается сферы (в точке M ). Теорема доказана. ▼

Так как сечение шара плоскостью есть круг, то можно доказать, что для шара выполняются следующие метрические соотношения:

— диаметр шара, делящий его хорду пополам, перпендикулярен этой хорде;

— отрезки всех касательных прямых, проведённых к шару из одной расположенной вне шара точки, равны между собой (они образуют поверхность конуса с вершиной в данной точке, а точки касания этих прямых — окружность основания этого конуса);

— произведение длин отрезков хорд шара, проходящих через одну и ту же внутреннюю точку шара, есть величина постоянная (равная R 2 – a 2 , где R — радиус шара, a — расстояние от центра шара до данной точки);

— если из одной и той же точки вне шара проведены к нему секущая и касательная, то произведение длины отрезка всей секущей на длину отрезка её внешней части равно квадрату длины отрезка касательной (и равно a 2 – R 2 , где R — радиус шара, a — расстояние от центра шара до данной точки).

19.6. Вписанные и описанные шары и сферы

Определение. Шар называется вписанным в цилиндр, если основания и каждая образующая цилиндра касаются шара (рис. 206).

Цилиндр в таком случае называется описанным около шара. В цилиндр можно вписать шар тогда и только тогда, когда он равносторонний.

Определение. Шар называется описанным около цилиндра, если основания цилиндра служат сечениями шара (рис. 207).

Цилиндр при этом называют вписанным в шар. Около любого цилиндра можно описать шар. Центром шара служит середина оси цилиндра, а радиус шара равен радиусу круга, описанного около осевого сечения цилиндра.

Определение. Шар называется описанным около конуса, если основание конуса — сечение шара, а вершина конуса принадлежит поверхности шара (рис. 208).

Конус при этом называют вписанным в шар.

Центр шара, описанного около конуса, совпадает с центром круга, описанного около осевого сечения конуса, а радиус шара равен радиусу этого круга.

Определение. Шар называется вписанным в конус, если основание и все образующие конуса касаются шара.

Конус при этом называют описанным около шара (рис. 209). Центр вписанного в конус шара совпадает с центром круга, вписанного в осевое сечение конуса, а радиус шара равен радиусу этого круга.

Определение. Шар называется вписанным в многогранник, если он касается всех граней многогранника.

Многогранник в таком случае называют описанным около шара (рис. 210).

Не во всякий многогранник можно вписать шар. Например, вписать шар можно в любую треугольную или правильную пирамиду. А в прямую призму, в основании которой лежит прямоугольник, не являющийся квадратом, шар вписать нельзя.

При нахождении радиуса r вписанного в многогранник шара (если таковой существует) удобно пользоваться соотношением

V многогр = • r • S полн. поверх .

Шар называется вписанным в двугранный угол, если он касается его граней. Центр вписанного в двугранный угол шара лежит на биссекторной плоскости этого двугранного угла. При этом для радиуса r шара, вписанного в двугранный угол, величины α этого угла и расстояния m от центра шара до ребра двугранного угла справедлива формула: r = m • sin . Этой формулой часто пользуются при решении задач.

Шар называется вписанным в многогранный угол, если он касается всех граней многогранного угла. При решении задач, в которых рассматриваются вписанные в многогранный угол шары, удобно пользоваться соотношением: r = m • sin , где r — радиус шара, вписанного в многогранный угол, m — расстояние от центра шара до ребра многогранного угла, α — величина двугранного угла при этом ребре.

Если все плоские углы трёхгранного угла равны по 60 ° , то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно 3 r ; если все плоские углы трёхгранного угла прямые, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно r . Эти соотношения часто используют при решении задач, в которых рассматриваются те или иные комбинации шаров с правильными тетраэдрами или прямоугольными параллелепипедами.

Определение. Шар называется описанным около многогранника, если все вершины многогранника принадлежат поверхности шара (рис. 211) . Многогранник при этом называют вписанным в шар.

Не около всякого многогранника можно описать шар. Например, около любой правильной или любой треугольной пирамиды шар описать можно, а около четырёхугольной пирамиды, в основании которой лежит ромб, не являющийся квадратом, шар описать нельзя (около ромба нельзя описать окружность). Более того, нельзя описать шар около любой наклонной призмы.

Вообще, для того чтобы около многогранника можно было описать шар, необходимо, чтобы около любой его грани можно было описать круг. При этом центр описанного шара может лежать как внутри многогранника, так и вне его или на его поверхности (даже на ребре многогранника), и проектируется в центр описанного около любой грани круга. Кроме того, перпендикуляр, опущенный из центра описанного около многогранника шара на ребро многогранника, делит это ребро (как хорду шара) пополам.

Мы уже говорили о пирамидах, все рёбра которых одинаково наклонены к основанию. Около таких пирамид всегда можно описать шар, центр которого лежит на луче, содержащем высоту пирамиды.

Высота h пирамиды, радиус R к описанного около основания пирамиды круга и радиус R описанного около этой пирамиды шара связаны соотношением:

( R – h ) 2 + = R 2 .

Приведём формулы для вычисления радиусов вписанных и описанных шаров для правильных многогранников с ребром a.

В задачах иногда ещё рассматривают шары, касающиеся всех рёбер данного многогранника. Для куба, например, такой шар существует и его радиус равен , где a — ребро куба.

19.7. Площади поверхностей шара и его частей

Часть шара, заключённая между секущей плоскостью и одной из двух частей его сферической поверхности, называется шаровым сегментом (рис. 212 и 214). Поверхность шарового сегмента называется сегментной поверхностью : она представляет собой часть шаровой поверхности, отсекаемую какой-нибудь плоскостью. Круг АВ, по которому плоскость пересекает шар, называется основанием шарового сегмента, а окружность этого круга — основанием сегментной поверхности. Отрезок ОС радиуса, перпендикулярного секущей плоскости, называется высотой шарового сегмента ( сегментной поверхности ) .

Часть шара, заключённая между двумя параллельными секущими плоскостями, называется шаровым слоем (см. рис. 212, 214). Поверхность шарового слоя называется шаровым поясом. Шаровой пояс — часть шаровой поверхности, заключённая между двумя параллельными секущими плоскостями. Перпендикуляр, проведённый из точки одного основания к плоскости другого, называется высотой шарового слоя ( шарового пояса ).

Сегментную поверхность и шаровой пояс можно рассматривать как поверхности вращения: в то время, как при вращении полуокружности CAA 1 D (см. рис. 212) вокруг диаметра CD образуется шаровая поверхность (сфера), при вращении дуги СА этой полуокружности вокруг того же диаметра образуется сегментная поверхность, а при вращении дуги AA 1 — шаровой пояс.

Тело, образованное при вращении кругового сектора с углом ϕ ( ϕ ° ) вокруг прямой, которая содержит диаметр круга, не имеющий с круговым сектором общих внутренних точек, называется шаровым сектором .

Из этого определения следует, что поверхность шарового сектора состоит из сегментной поверхности и боковой поверхности конуса (рис. 213, а , б ) или из поверхности шарового пояса и боковых поверхностей двух конусов (рис. 213, в, г ).

На рисунке 214 изображены различные элементы шара и сферы (шаровой сектор имеет простейший вид).

Рассмотрим вопрос о вычислении площадей сферы, сегментной поверхности, шарового пояса и шарового сектора.

а) Площадь сферы. Пусть ABCDEF — правильная ломаная линия, вписанная в данную полуокружность; a — длина её апофемы (рис. 215). При вращении полуокружности вокруг её диаметра AF образуется сфера, а при вращении ломаной ABCDEF вокруг этого же диаметра AF образуется некоторая поверхность Ф .

За площадь сферы, образованной вращением полуокружности вокруг её диаметра, принимают предел, к которому стремится площадь поверхности Ф, образованной вращением вокруг того же диаметра правильной n- звенной ломаной линии, вписанной в полуокружность, при n → + ∞ ( число сторон неограниченно возрастает ).

Поверхность Ф является объединением поверхностей, образованных вращением звеньев ломаной линии, вписанной в полуокружность, вокруг её диаметра. Этими поверхностями являются боковые поверхности либо конуса (для первого и последнего звеньев ломаной), либо цилиндра (для звеньев, параллельных оси вращения; их может и не быть), либо усечённого конуса (для всех остальных звеньев ломаной).

При вычислении площадей получившихся поверхностей воспользуемся следствиями из теорем 26, 27, 29. Площадь S i ( i = 1, 2, . n ) поверхности, образованной вращением любого звена, равна произведению 2 π , расстояния b i от середины звена до центра сферы и длины m i проекции этого звена на ось вращения, т. е. S i вращ = 2 π • b i • m i .

Так как ломаная — правильная, то все b i равны апофеме a n данной n- звенной ломаной, а m 1 + m 2 + m 3 + . + m n = 2 R и S 1 + S 2 + S 3 + . + S n = 4 π • a n • R . Причём a n = , где p n — периметр данной ломаной. Поскольку ограниченная переменная величина при n → + ∞ становится бесконечно малой, то при n → ∞ апофема a n стремится к радиусу R полуокружности.

Следовательно, предел площади поверхности Ф при n → ∞ равен 4 π R • R = 4 π R 2 . Этот предел и принимается за величину площади сферы радиуса R :

S сферы = 4 π R 2 .

б) Площади сегментной поверхности и шарового пояса. Если правильная ломаная вписана не в полуокружность, а в некоторую её часть, например в дугу AD (см. рис. 215), при вращении которой образуется сегментная поверхность, то рассуждения, аналогичные предыдущим, приводят к выводу:

S сегм. поверх = 2 π Rh ,

где h — высота сферического сегмента.

Если же ломаная вписана в дугу ВЕ (см. рис. 215), при вращении которой образуется шаровой пояс, то получим:

S шар. пояса = 2 π Rh ,

где h — высота шарового пояса.

Проделайте эти рассуждения самостоятельно.

в) Площадь поверхности шарового сектора. Эта площадь может быть получена как сумма площадей поверхности сферического сегмента и боковой поверхности одного конуса (см. рис. 213, а, б ) или как сумма площадей поверхности сферического слоя и боковых поверхностей двух конусов (см. рис. 213, в, г ).

Рассмотрим частный случай (см. рис. 213, а, б ). Если R — радиус сферы, h — высота шарового сегмента, то площадь боковой поверхности конуса с вершиной в центре сферы, образующей R , и радиусом основания (докажите это) равна π R , а площадь сегментной поверхности равна 2 π Rh. Значит, для площади шарового сектора справедлива формула

S шар. сект = π R (2 h + ) .

 ЗАДАЧА (3.418). Основанием треугольной пирамиды SABC является равносторонний треугольник АВС , сторона которого равна 4. Известно также, что AS = BS = , a SC = 3. Найти площадь сферы, описанной около этой пирамиды.

Решени е. Решим эту задачу двумя методами.

Первый метод ( геометрич е ски й). Пусть точка О — центр сферы, описанной около данной пирамиды; D — точка пересечения медиан правильного △ АВС ; точка Е — середина отрезка АВ (рис. 216).

Центр О сферы равноудалён от всех вершин △ АBС, поэтому принадлежит прямой, проходящей через точку D перпендикулярно плоскости АВС.

Так как точка Е — середина отрезка АВ, то SE ⟂ АВ ( AS = BS ) и СЕ ⟂ АВ ( △ АВС — правильный). Значит, по признаку перпендикулярности прямой и плоскости AB ⟂ ( CSE ) , поэтому ( CSE ) ⟂ ( ABC ) (по признаку перпендикулярности двух плоскостей). Это означает, что прямая OD, а следовательно, и точка О — центр сферы — лежат в плоскости CSE.

Точка D является центром окружности, описанной около △ АВС. (По этой окружности плоскость АВС пересекает сферу, описанную около данной пирамиды.) Если L — точка пересечения прямой СЕ и упомянутой окружности, то CL — её диаметр. Найдём длину диаметра CL.

В правильном △ AВС имеем: CE = = 2 ; CD = СЕ = . Тогда CL = 2 CD = .

Далее △ BSE ( ∠ BES = 90 ° ): SE 2 = SB 2 – BE 2 = 19 – 4 = 15 (по теореме Пифагора); △ SEC (по теореме косинусов):

cos C = = = ;

△ SLC (по теореме косинусов):

SL 2 = SC 2 + CL 2 – 2 SC • CL • cos C = ⇒ SL = .

Плоскость CSL проходит через центр О сферы, следовательно, пересекает сферу по большой окружности, которая описана около △ CSL. Значит, радиус R этой окружности равен радиусу сферы, описанной около данной пирамиды. Найдём длину радиуса R.

В треугольнике CSL имеем = 2 R. Так как в этом треугольнике cos C = , то sin C = = . Тогда R = = : = .

Находим площадь Q сферы:

Q = 4 π R 2 = 4 π • = π .

Второй метод ( коо р динатны й). Введём в пространстве декартову прямоугольную систему координат так, чтобы её начало совпадало с вершиной А данной пирамиды, направление оси абсцисс — с направлением луча АС, ось аппликат была перпендикулярна плоскости основания АВС пирамиды (рис. 217).

В этой системе координат вершины основания пирамиды имеют координаты: А (0; 0; 0), B (2; 2 ; 0), C (4; 0; 0).

Обозначив через х, у, z координаты вершины S пирамиды, найдём их из условий: AS = BS = , CS = 3 .

AS 2 = x 2 + y 2 + z 2 = 19,
ВS 2 = ( x – 2) 2 + ( y – 2 ) 2 + z 2 = 19,
C S 2 = ( x – 4) 2 + y 2 + z 2 = 9.

Решая систему уравнений

x 2 + y 2 + z 2 = 19, ( x – 2) 2 + ( y – 2 ) 2 + z 2 = 19, ( x – 4) 2 + y 2 + z 2 = 9,

находим: х = , у = , z = .

Таким образом, вершина S имеет следующие координаты:

S .

Пусть центр O сферы имеет координаты a, b, с, а её радиус равен R. Так как сфера описана около пирамиды SABC, то OA 2 = OB 2 = OC 2 = OS 2 = R 2 . Это соотношение в координатном виде равносильно системе уравнений

a 2 + b 2 + c 2 = R 2 , ( a – 2) 2 + ( b – 2 ) 2 + c 2 = R 2 , + + = R 2 , ( a – 4) 2 + b 2 + c 2 = R 2 .

Вычитая из первого уравнения четвёртое, получаем a = 2, после чего, вычитая из первого уравнения второе, получаем b = .

После вычитания третьего уравнения системы из первого её уравнения получаем:

= 0.

Подставив в это уравнение вместо a и b найденные их значения, получаем с = . Отсюда: R 2 = a 2 + b 2 + c 2 = 4 + + = . Тогда искомая площадь Q сферы равна:

Q = 4 π R 2 = π .

Ответ: π (кв. ед.).

19.8. Объёмы шара и его частей

Рассмотрим фигуру, образованную вращением равнобедренного прямоугольного треугольника с гипотенузой 2 R вокруг прямой, проходящей через вершину прямого угла параллельно гипотенузе (рис. 218, а ). Объём этой фигуры равен разности объёма цилиндра с высотой 2 R , радиусом основания R и удвоенного объёма конуса высоты R , радиуса основания R :

V = π • R 2 • 2 R – 2 • π • R 2 • R = π • R 3 . (*)

Шар радиуса R (рис. 218, б ) и образованную выше фигуру вращения расположим между двумя параллельными плоскостями, расстояние между которыми равно 2 R . Шар при этом будет касаться каждой из данных плоскостей, а фигуру вращения расположим так, чтобы её ось вращения была перпендикулярна этим плоскостям (см. рис. 218). (Плоскость, которая содержит верхнее основание цилиндра и касается сферы в точке N , на рисунке не изображена.)

Будем пересекать наши фигуры плоскостями, параллельными данным плоскостям и удалёнными от центра шара на расстояние x (0 ⩽ x ⩽ R ).

При х = 0 площади сечений обеих фигур равны π • R 2 ; при х = R площади сечений равны нулю. В остальных случаях площадь сечения шара равна π • ( ) 2 = π • ( R 2 – x 2 ), а площадь сечения другой фигуры (ею является кольцо) равна π • R 2 – π • x 2 . Следовательно, площади равноудалённых от центра шара сечений рассматриваемых фигур равны (относятся, как 1 : 1). Поэтому на основании принципа Кавальери равны и объёмы этих тел. Тогда на основании (*):

V шара = • π • R 3 ,

гдe R — радиус шара.

Для получения объёма шарового сегмента высоты h рассмотрим предыдущую ситуацию для R – h ⩽ x ⩽ R (при h R ) (рис. 218, 219). Применяя принцип Кавальери, получим: объём шарового сегмента равен разности объёма цилиндра высоты h и радиуса основания R и объёма усечённого конуса высоты h и радиусов оснований R и R – h , т. е.

V = π • h • R 2 – π • h • ( R 2 + R • ( R – h ) + ( R – h ) 2 ) =
= π • h 2 • (3 R – h ) .

При h > R объём шарового сегмента можно найти как разность объёма шара и объёма шарового сегмента высоты 2 R – h (рис. 220): V = π • R 3 – • π • (2 R – h ) 2 • (3 R – (2 R – h )) = π • h 2 (3 R – h ) , т. е. получаем ту же самую формулу. Подставляя в эту формулу h = R , получим V = π • R 2 (3 R – R ) = π • R 3 , что соответствует объёму полушара.

Мы показали, что в шаре радиуса R объём любого шарового сегмента высоты h может быть вычислен по формуле:

V шар. сегм = π • h 2 • (3 R – h ) ,

или в другом виде

V шар. сегм = π • h 2 • .

📹 Видео

Стереометрия "с нуля" Урок 7. Теорема о трех перпендикулярахСкачать

10 класс, 21 урок, Угол между прямой и плоскостьюСкачать