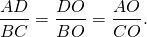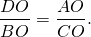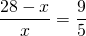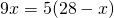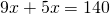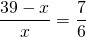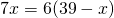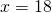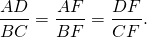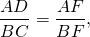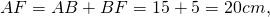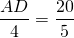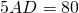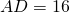Из трапеции 4 треугольника

Математика | 10 — 11 классы

Как разделить трапецию двумя отрезками на четыре треугольника.

Проведи диоганали и всё).

Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Как разделить треугольник двумя отрезками так, чтобы получить два треугольника, один четырёхугольник и один пятиугольник?

Как разделить треугольник двумя отрезками так, чтобы получить два треугольника, один четырёхугольник и один пятиугольник?

Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Как разделить трапецию на 4 равных треугольника двумя линиями?

Как разделить трапецию на 4 равных треугольника двумя линиями?

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Разделить четырёхугольник двумя прямыми на четыре треугольника?

Разделить четырёхугольник двумя прямыми на четыре треугольника.

Видео:8 класс, 6 урок, ТрапецияСкачать

Как разделить треугольник двумя отрезками так, чтобы получить два треугольника, один четырёхугольник и один пятиугольник?

Как разделить треугольник двумя отрезками так, чтобы получить два треугольника, один четырёхугольник и один пятиугольник?

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Как разделить четырёх угольник двумя линиями на четыре одинаковых треугольника?

Как разделить четырёх угольник двумя линиями на четыре одинаковых треугольника.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Разделить (не равносторонняя трапеция) двумя отрезками на 4 одинаковых треугольника?

Разделить (не равносторонняя трапеция) двумя отрезками на 4 одинаковых треугольника.

Видео:Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

Разделить четырехугольник на четыре равных треугольника двумя отрезками?

Разделить четырехугольник на четыре равных треугольника двумя отрезками.

Видео:Геометрия 8 класс (Урок№4 - Трапеция)Скачать

Как разделить треугольник на два треугольника четырёх угольник и пяти угольник двумя отрезками?

Как разделить треугольник на два треугольника четырёх угольник и пяти угольник двумя отрезками.

Видео:Площадь прямоугольника. Как найти площадь прямоугольника?Скачать

Как разделить разностороннюю трапецию двумя отрезками на четыре одинаковых треугольника?

Как разделить разностороннюю трапецию двумя отрезками на четыре одинаковых треугольника.

Видео:Диагонали трапеции и точка их пересеченияСкачать

Как разделить равнобедренную трапецию двумя линиями , чтобы получить 4 одинаковых треугольника?

Как разделить равнобедренную трапецию двумя линиями , чтобы получить 4 одинаковых треугольника.

Вы зашли на страницу вопроса Как разделить трапецию двумя отрезками на четыре треугольника?, который относится к категории Математика. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

1)100% — 15% = 85% 2)120•85% = 10. 200(р. ) Ответ : инженер получил 10. 200 рублей премию.

56 : 28 = 2(р) 4×2 = 8(м). Ответ : 8м.

28 / 4 = 7 рублей стоит 1 метр ленты 56 / 7 = 8 лент Ответ : на 56 руб можно купить 8 м ленты.

S = a * b s = 4 * 6 = 24 это только площадь.

А = 4 см, в = 6 см, S = а * в, S = 4 * 6 = 24 см², значит длинами сторон других прямоугольников с такой же площадью могут быть : а = 2, в = 12, а = 3, в = 8.

4 / 3 = 1, 33 * 100 = 133% вообще получается 1, 3(3) в периоде.

LXXIV (римские) = 74(арабские).

Это вроде число 74, но это не точно.

1)350 : 10 = 35(дц) синий флаг 2)35 + 75 = 110(дц) белый флаг 3)350 + 35 + 110 = 495(ш) вместе Ответ : 495шелка.

Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Видео:Можно ли так повернуть налево?/Три задачки для опытных водителейСкачать

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Видео:8 класс, 15 урок, Площадь трапецииСкачать

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Основания трапеции равны 4 и 10 Найдите больший из отрезков на которые делит среднюю линию диагональСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Трапеция, решение задач. Вебинар | МатематикаСкачать

Подобные треугольники в трапеции

Рассмотрим базовые задачи на подобные треугольники в трапеции.

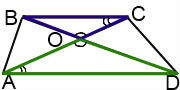
I. Точка пересечения диагоналей трапеции — вершина подобных треугольников.

Рассмотрим треугольники AOD и COB.

Визуализация облегчает решение задач на подобие. Поэтому подобные треугольники в трапеции выделим разными цветами.

1) ∠AOD= ∠ COB (как вертикальные);

2) ∠DAO= ∠ BCO (как внутренние накрест лежащие при AD ∥ BC и секущей AC).

Следовательно, треугольники AOD и COB подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Одна из диагоналей трапеции равна 28 см и делит другую диагональ на отрезки длиной 5 см и 9 см. Найти отрезки, на которые точка пересечения диагоналей делит первую диагональ.

AO=9 см, CO=5 см, BD=28 см. BO =?, DO- ?

Доказываем подобие треугольников AOD и COB. Отсюда

Выбираем нужные отношения:

Пусть BO=x см, тогда DO=28-x см. Следовательно,

BO=10 см, DO=28-10=18 см.

Ответ: 10 см, 18 см.

Известно, что О — точка пересечения диагоналей трапеции ABCD (AD ∥ BC). Найти длину отрезка BO, если AO:OC=7:6 и BD=39 см.

Аналогичн0, доказываем подобие треугольников AOD и COB и

Пусть BO=x см, тогда DO=39-x см. Таким образом,

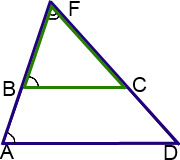
II. Продолжения боковых сторон трапеции пересекаются в точке.

Аналогично задаче I, рассмотрим треугольники AFD и BFC:

2) ∠ DAF= ∠ CBF (как соответственные углы при BC ∥ AD и секущей AF).

Следовательно, треугольники AFD и BFC подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Продолжения боковых сторон AB и CD трапеции ABCD пересекаются в точке F. Меньшее основание BC равно 4 см, BF=5 см, AB=15 см. Найти большее основание трапеции.

Доказываем, треугольники AFD и BFC — подобны.

В следующий раз рассмотрим задачи на отношение площадей подобных треугольников.

📽️ Видео

Коллаб 4 каналов. 4 замечательные точки трапецииСкачать

35. Геометрия на ЕГЭ по математике. Трапеция.Скачать

Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать