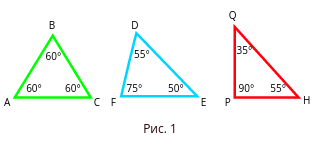Сумма углов треугольника — это сумма
всех внутренних углов треугольника.
Так, как углы измеряются в градусах, соответственно значение
суммы углов треугольника также измеряется в градусах.
Сумма углов треугольника есть величина постоянная,
неизменяемая, она равна 180 градусам, вне зависимости
от вида рассматриваемого треугольника.
На рисунке 1 изображены равносторонний,
разносторонний и прямоугольный треугольники,
их суммы внутренних углов равны 180 градусам.
Также, существует теорема, которая доказывает
утверждение о том, что сумма углов треугольника
180 градусов, она называется теоремой
о сумме углов треугольника.
Теорема о сумме углов треугольника — это теорема в
геометрии о сумме углов произвольного треугольника на плоскости.
- Каков максимально возможный угол в треугольнике?
- Какой угол в треугольнике самый большой?
- Какой правильный многоугольник имеет наибольший внутренний угол?
- Как найти угол треугольника?
- Какой угол самый маленький?
- Какая сторона треугольника самая длинная?
- Как найти недостающий угол в треугольнике?
- Могут ли 22 градуса быть внутренним углом правильного многоугольника?
- Как называется 50-сторонний многоугольник?
- Есть ли минимальное количество острых внутренних углов?
- Как найти угол треугольника с 3 сторонами?
- Как найти угол треугольника с двумя углами?
- Как найти угол прямоугольного треугольника?
- Почему самая длинная сторона противоположна наибольшему углу?
- Как называется самая длинная сторона треугольника?
- Какой треугольник имеет максимальную площадь?
- Какая самая короткая сторона прямоугольного треугольника?
- Какая сторона треугольника A?
- Работает ли теорема Пифагора для каждого треугольника?
- Как определить угол наклона?
- Как решить треугольник SSA?
- Как решить треугольник SAS?
- Может ли треугольник иметь только один острый угол?
- Может ли треугольник не иметь острых углов?
- Треугольник. Формулы определения и свойства треугольников.
- Определение треугольника
- Классификация треугольников
- 1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
- 2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
- 3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
- 4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
- 5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
- 6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
- Свойства треугольника
- 1.Свойства углов и сторон треугольника.
- 2.Теорема синусов.
- 3. Теорема косинусов.
- 4. Теорема о проекциях
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
Видео:Почему в треугольнике против большей стороны - больший угол ➜ ДоказательствоСкачать

Каков максимально возможный угол в треугольнике?
Вы предполагаете, что наименьший возможный угол равен 1, а наибольший возможный угол равен 178 для треугольника.
Треугольник с такими углами имеет углы 1, 1, 178, так как сумма всех углов треугольника равна 180.
Мы можем взять угол меньше 1.
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Какой угол в треугольнике самый большой?
В треугольнике: самая короткая сторона всегда противоположна наименьшему внутреннему углу. Самая длинная сторона всегда противоположна наибольшему внутреннему углу.
Видео:Внешний угол треугольникаСкачать

Какой правильный многоугольник имеет наибольший внутренний угол?
Многоугольник с наименьшим числом сторон — это треугольник. Правильный треугольник будет равносторонним треугольником, и каждый из его углов будет составлять 60 градусов, и это наименьший внутренний угол. Наибольший внутренний угол правильного многоугольника не ограничен.
Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Как найти угол треугольника?
Ответ: Если вы знаете два угла, вы можете вычислить третий, поскольку сумма всех углов равна 180 градусам. Если стороны — a, b, а гипотенуза — c (противоположный угол A), а углы — A, B и C, то Sin A = a / c, поэтому a = cSin A. Также Cos A = b / c, так что b = cCos A.
Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Какой угол самый маленький?
Всегда помните, что самый маленький угол в треугольнике всегда противоположен самой короткой стороне. Кроме того, самый большой угол всегда противоположен самой длинной стороне. Ответ: Наименьший угол составляет 55.49 градуса с округлением до двух знаков после запятой.
Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Какая сторона треугольника самая длинная?
Гипотенуза всегда противоположна прямому углу и всегда является самой длинной стороной треугольника.
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Как найти недостающий угол в треугольнике?
Шаг 2: сложите два известных угла внутри треугольника. Чтобы определить неизвестный угол, обязательно используйте общую сумму 180 °. Если даны два угла, сложите их, а затем вычтите из 180 °. Если два угла одинаковы и неизвестны, вычтите известный угол из 180 °, а затем разделите на 2.
Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Могут ли 22 градуса быть внутренним углом правильного многоугольника?
Если 22 ° — внутренний угол, то 180 ° — 22 °, т.е. 158 ° — внешний угол. Таким образом, 22 ° не может быть внутренним углом правильного многоугольника.
Видео:Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать

Как называется 50-сторонний многоугольник?
В геометрии пятиугольник, или пятиугольник, или 50-угольник — это многоугольник с пятидесяти гранями.
Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Есть ли минимальное количество острых внутренних углов?
Любой выпуклый многоугольник может иметь не более трех острых внутренних углов. Для любого острого внутреннего угла внешний угол будет больше 3 градусов. Сумма всех внешних углов в многоугольнике всегда равна 90 градусам, поэтому не может быть 360 или более острых внутренних углов.
Видео:№236. Сравните углы треугольника ABC и выясните, может ли быть угол А тупым, если: а) АВСкачать
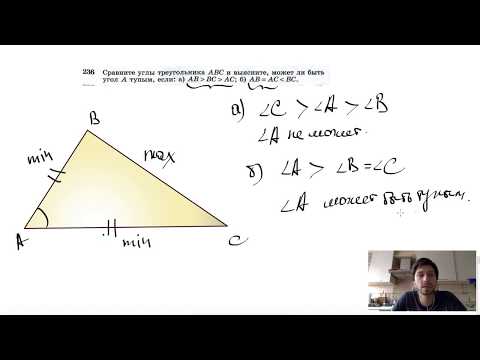
Как найти угол треугольника с 3 сторонами?
Пример
- Шаг 1 Нам известны две стороны: Соседняя (6,750) и Гипотенуза (8,100).
- Шаг 2 SOHCAHTOA сообщает нам, что мы должны использовать косинус.
- Шаг 3 Вычислить смежное значение / гипотенуза = 6,750 / 8,100 = 0.8333.
- Шаг 4 Найдите угол на вашем калькуляторе, используя cos-1 0.8333:
Видео:В треугольнике АВС углы А и С равны 40 и 60 градусовСкачать

Как найти угол треугольника с двумя углами?
Чтобы найти третий угол треугольника, когда известны два других угла, вычтите количество градусов в двух других углах из 180o.
Видео:Найдите угол: задача по геометрииСкачать

Как найти угол прямоугольного треугольника?
Ключевые моменты
- Теорема Пифагора, a2 + b2 = c2, a 2 + b 2 = c 2, используется для определения длины любой стороны прямоугольного треугольника.
- В прямоугольном треугольнике один из углов имеет значение 90 градусов.
- Самая длинная сторона прямоугольного треугольника называется гипотенузой, и это сторона, противоположная углу в 90 градусов.
Видео:№228. Найдите углы равнобедренного треугольника, если один из его углов равен: а) 40°Скачать

Почему самая длинная сторона противоположна наибольшему углу?
Как вы могли догадаться, наибольший угол будет противоположным 18, потому что это самая длинная сторона. Следовательно, величина угла в середине будет противоположной 13. Теорема: если одна сторона треугольника длиннее другой стороны, то угол, противоположный длинной стороне, будет больше, чем угол, противоположный более короткой стороне.
Видео:Как найти углы в треугольникеСкачать
Как называется самая длинная сторона треугольника?
Видео:ВНЕШНИЕ УГЛЫ ТРЕУГОЛЬНИКА 😉 #shorts #математика #егэ #огэ #профильныйегэСкачать

Какой треугольник имеет максимальную площадь?
Свойство максимальной площади равносторонних треугольников. Частный случай изопериметрической теоремы говорит нам, что среди всех треугольников с одинаковым периметром равносторонний имеет наибольшую площадь.
Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Какая самая короткая сторона прямоугольного треугольника?
Третья сторона — сторона, противоположная прямому углу — называется гипотенузой прямоугольного треугольника. Две более короткие стороны обычно называют «ногами». Эта формула называется теоремой Пифагора в честь Пифагора.
Видео:Углы треугольникаСкачать
Какая сторона треугольника A?
Стороны треугольника известны следующим образом: гипотенуза — это сторона, противоположная прямому углу, или определяемая как самая длинная сторона прямоугольного треугольника, в данном случае h. Противоположная сторона — это сторона, противоположная интересующему нас углу, в данном случае a.
Видео:IBLS — Существует ли треугольник, у которого все углы прямые? #shortsСкачать

Работает ли теорема Пифагора для каждого треугольника?
Теорема Пифагора утверждает, что для всех прямоугольных треугольников «квадрат гипотенузы равен сумме квадратов на двух других сторонах». Теорема Пифагора работает только для прямоугольных треугольников, поэтому вы можете использовать ее, чтобы проверить, имеет ли треугольник прямой угол или нет.
Видео:В треугольнике ABC углы А,В и С относятся как 1 :1:7 .Найти углы треугольника ABC.7 кл.ОгэСкачать

Как определить угол наклона?
Если два угла треугольника имеют размеры 60 и 80 градусов, сложите числа вместе, чтобы получить сумму 140. Затем вычтите эту сумму из общей меры углов для треугольника, которая составляет 180 градусов: 180 — 140 = 40 градусов.
Как решить треугольник SSA?
Решение треугольников SSA
- сначала используйте Закон синусов, чтобы вычислить один из двух других углов;
- затем добавьте три угла к 180 °, чтобы найти другой угол;
- наконец, снова используйте Закон синуса, чтобы найти неизвестную сторону.
Как решить треугольник SAS?
Решение треугольников SAS
- используйте Закон косинусов для вычисления неизвестной стороны,
- затем используйте Закон синусов, чтобы найти меньший из двух других углов,
- а затем добавьте три угла к 180 °, чтобы найти последний угол.
Может ли треугольник иметь только один острый угол?
Ни одного острого угла !! Потому что один острый означает два тупых угла, каждый больше 90 градусов. Два тупых угла в сумме составляют более 180 градусов. Но три угла треугольника должны составлять ровно 180 градусов. Таким образом, должно быть как минимум два острых угла.
Может ли треугольник не иметь острых углов?
Поскольку сумма углов треугольника в евклидовой геометрии должна составлять 180 °, ни один евклидов треугольник не может иметь более одного тупого угла. Острый и тупой треугольники — это два разных типа наклонных треугольников — треугольники, которые не являются прямыми треугольниками, потому что у них нет угла 90 °.
Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны: