Из точки м к окружности

Видео:№150. Даны окружность, точка А, не лежащая на ней, и отрезок PQ. Постройте точку М на окр-тиСкачать

Ваш ответ

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

решение вопроса

Видео:Точки на числовой окружностиСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,835
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Из точки М к окружности с центром О и радиусом 8см проведены касательные AM и BM (A и B — Точки касания)?

Геометрия | 5 — 9 классы

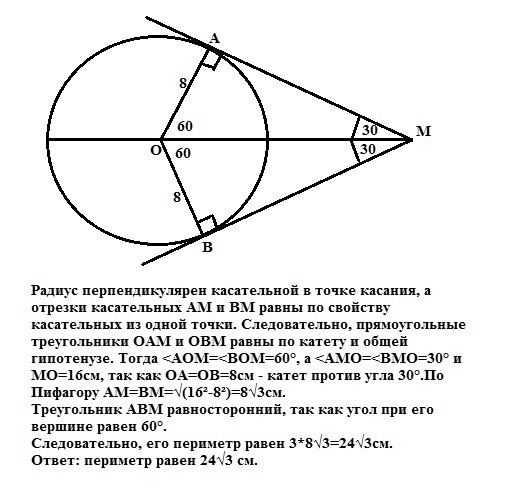
Из точки М к окружности с центром О и радиусом 8см проведены касательные AM и BM (A и B — Точки касания).

Найдите периметр треугольника ABM, если угол AOB = 120 градусов.

Радиус перпендикулярен касательной в точке касания, а отрезки касательных АМ и ВМ равны по свойству касательных из одной точки.

Следовательно, прямоугольные треугольники ОАМ и ОВМ равны по катету и общей гипотенузе.

Тогда &lt ; AOM = &lt ; BOM = 60°, а &lt ; АМО = &lt ; BMO = 30° и МО = 16см, так как ОА = ОВ = 8см — катет против угла 30°.

По Пифагору АМ = ВМ = √(16² — 8²) = 8√3см.

Треугольник АВМ равносторонний, так как угол при его вершине равен 60°.

Следовательно, его периметр равен 3 * 8√3 = 24√3см.

Ответ : периметр равен 24√3 см.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Из точки А к окружности с центром О проведены касательные АВ и АС В и С точки касания найдите ВАС и если ВОА = 80 градусов?

Из точки А к окружности с центром О проведены касательные АВ и АС В и С точки касания найдите ВАС и если ВОА = 80 градусов.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Из точки А проведены две касательные окружности с центром в точке О?

Из точки А проведены две касательные окружности с центром в точке О.

Найдите радиус окружности если угол между касательными равен 60 градусов, а расстояние от точки А до точки О равно 8.

Видео:2017 на окружности по разные стороны от диаметра AB взяты Точки M и NСкачать

Из точки B к окружности с центром О проведена касательная, A — точка касания?

Из точки B к окружности с центром О проведена касательная, A — точка касания.

Найдите радиус окружности, если AB = 6√3, угол ABO = 30°.

Видео:Если из точки M проведены две касательные ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Из точки А, лежащей вне окружности с центром в точке О, проведены две касательные?

Из точки А, лежащей вне окружности с центром в точке О, проведены две касательные.

Найдите угол между ними, если угол между радиусами этой окружности, проведенный в точке касания, равен 120°.

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Из точки а к окружности с центром о проведена касательная?

Из точки а к окружности с центром о проведена касательная.

Точка в — точка касания.

Найдите длину отрезка оа если радиус окружности равен 4, 5 а угол ВОА = 60.

Видео:Геометрия. ОГЭ по математике. Задание 15Скачать

Из точки М к окружности с центром О проведены касательные МА и МВ, А и В — точки касания , Угол АМВ = 70 градусов ?

Из точки М к окружности с центром О проведены касательные МА и МВ, А и В — точки касания , Угол АМВ = 70 градусов !

Найдите углы треугольника ОВМ.

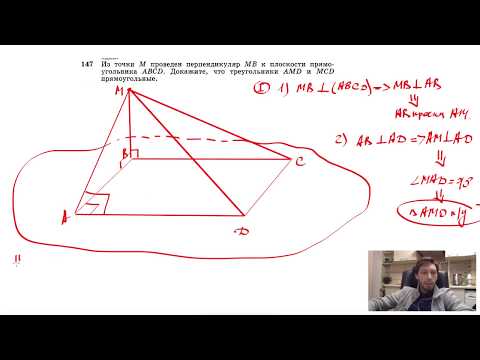
Видео:№147. Из точки М проведен перпендикуляр МВ к плоскости прямоугольника ABCD. Докажите, чтоСкачать

К окружности с центром O проведена касательная BA (A — точка касания)?

К окружности с центром O проведена касательная BA (A — точка касания).

Известно, что угол OBC = 130 градусам.

Найдите угол AOB.

Видео:Из точки С проведены две касательные к окружности с центром в точке ОСкачать

Окружности с центром точке О проведена касательная АВ, А — точка касания Найдите радиус окружности , если ОВ = 4см, уголАОВ = бетта?

Окружности с центром точке О проведена касательная АВ, А — точка касания Найдите радиус окружности , если ОВ = 4см, уголАОВ = бетта.

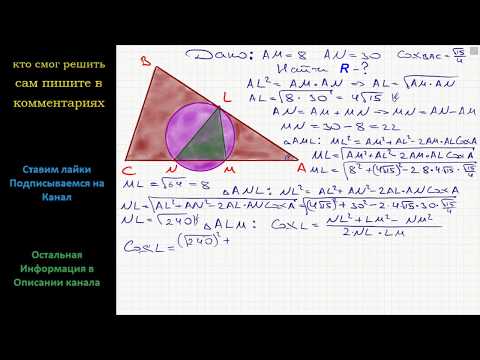
Видео:Задача№25 ОГЭ Точка M и N лежат на стороне АС. Найдите радиус окружности, если cos ВАС ...Скачать

К окружности с центром О проведена касательная АР, Р — точка касания?

К окружности с центром О проведена касательная АР, Р — точка касания.

найдите радиус окружности, если ОА = 15, АР = 12 Из точки А к окружности с центром О проведены две касательные, К и Р — точки касания.

Известно, что угол КАР = 82 градуса.

Найдите угол РОА К окружности проведены касательные РМ и РН, М и Н — точки касания.

Найдите угол НМР, если угол МРН = 40 градусов К окружности с центром в точке О проведена касательная BT Т точка касания .

Найдите площадь треугольника BОТ если угол BОТ равен 60 градусов, а радиус окружности равен 2 К окружности с центром О проведена касательные СМ и СN М и N точки касания.

Отрезки СО и МN пересекаются в точке А.

Найдите длину отрезка MN, если СМ = 13, АС = 12 СТАВЛЮ34 ; БАЛА НАДО РЕШИТЬ КАК МОЖНО БЫСТРЕЙ ЗАВТРА УЖЕ СДАВАТЬ!

Видео:ОГЭ Задание 25 Две окружностиСкачать

Из точки М к окружности с центром О и радиусом 8см проведены касательные АМ и ВМ (А и В — точки касания)?

Из точки М к окружности с центром О и радиусом 8см проведены касательные АМ и ВМ (А и В — точки касания).

Найдите периметр треугольника АВМ, если угол АОВ = 120°.

Вы зашли на страницу вопроса Из точки М к окружности с центром О и радиусом 8см проведены касательные AM и BM (A и B — Точки касания)?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

1. сумма∠NMP и ∠MNT — 180°⇒это односторонние углы, NK║MP 2. ∠PKT и∠PKB — смежные, тогда∠РКТ = 180° — 68° = 112° 3. NB||MP, РТ — секущая, ∠MPK = 180° — 112° = 68° 4. PT — биссектриса⇒∠MPT и ∠KPT = 68° : 2 = 34° 5. Углы KTP и MPT — внутренние разно..

(ну как — то так) т. К. треугольник равнобедренный, то углы при основании равны. 2 решения я придумал.

А)3х = 90 х = 30 градусов. Б)x + x / 8 = 90 9x / 8 = 90 9x = 720 x = 80 градусов.

Решение смотри в файлах.

Ответ : решение представлено на фотоОбъяснение .

Х (см) — наибольшая сторона (х — 2) (см) — вторая сторона (х — 4) (см) — третьясторона (х — 6) (см) — четвертая сторона Периметр четырехугольника = 132 см, с. У. х + х — 2 + х — 4 + х — 6 = 132 4х — 12 = 132 4х = 132 + 12 4х = 144 х = 36(см) — наибо..

Обозначим большую сторону через x, тогда три другие (x — 2), (x — 4) и (x — 6). Периметр — это сумма длин всех сторон, значит x + x — 2 + x — 4 + x — 6 = 132 4x — 12 = 132 4x = 144 x = 36 см — большая сторона Три другие стороны 34 см, 32 см, 30 см.

S = 1 / 2(a + b)×h = 1 / 2×( 3 + 5)×4 = 1 / 2×8×4 = 16 Ответ : 16.

∠1 + ∠2 + ∠3 = 5∠4 ∠1 + ∠2 + ∠3 + ∠4 = 6∠4 6∠4 = 360º ∠4 = 60º.

В = 24 + 31 = 55 А = 180 — (90 + 31) = 59(теорема о сумме углов треугольника) С = 180 — 90 — 24 = 66(Теорема о сумме углов треугольника).

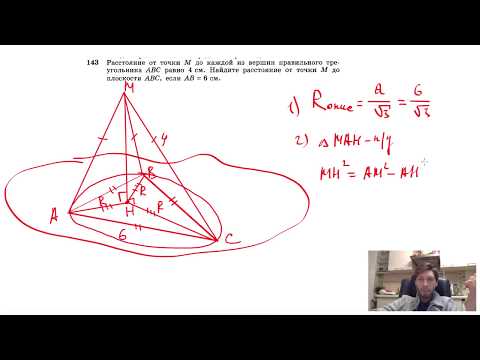
Видео:№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать

Касательная к окружности

О чем эта статья:

Видео:Быстрый разбор задания по геом| На окружности по разные стороны от диаметра AB взяты точки M и N.Скачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Физика - движение по окружностиСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

📹 Видео

Геометрия Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 8 и 30 отСкачать

Геометрия На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что угол NBAСкачать

№785. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD.Скачать