Из точки а к окружности проведены касательная ав 12см

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Ваш ответ

Видео:Геометрия Из одной точки проведены две касательные к окружности. Длина каждой касательной 12 см, аСкачать

решение вопроса

Видео:Из точки A проведены две касательные к окружности ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,049
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№635. Через точку А окружности проведены касательная и хорда, равная радиусу окружности.Скачать

ПОМОГИТЕ ПЛИЗ К окружности с центром в точке о проведены касательная ав и секущая ао Найдите радиус окружности, если AB = 12 см, AO = 13 см?

Геометрия | 5 — 9 классы

ПОМОГИТЕ ПЛИЗ К окружности с центром в точке о проведены касательная ав и секущая ао Найдите радиус окружности, если AB = 12 см, AO = 13 см.

Секущая проведена через центр окружности.

Касательная касается под углом — 90 градусов соединяешь О и В и получается прямоугольный треугольник.

Далее по теореме пифагора АВ = корень из 169 — 144 и получается корень из 25 а это 5 вот и все решение).

Видео:Геометрия Из точки А, не лежащей на окружности, проведены к ней касательная и секущая. Расстояние отСкачать

К окружности с центром в точке О проведены касательная AB и секущая АО?

К окружности с центром в точке О проведены касательная AB и секущая АО.

Найдите радиус окружности, если AB = 15см, АО = 17см.

Видео:Геометрия Из внешней точки к окружности проведены секущая длиной 12 см и касательная, длина которойСкачать

К окружности с центром в точке О проведены касательная AB и секущая AO?

К окружности с центром в точке О проведены касательная AB и секущая AO.

Найдите радиус окружности, если AB = 12 см, AO = 13 см.

Видео:№658. Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая ADСкачать

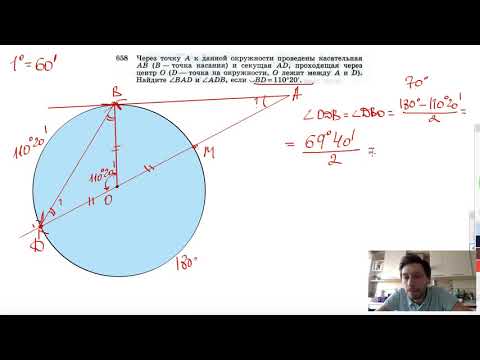
К окружности с центром в точке О проведены касательная AB и секущая AO?

К окружности с центром в точке О проведены касательная AB и секущая AO.

Найдите радиус окружности, если AB = 12 см, AO = 13 см.

Видео:Из точки A проведены две касательные к окружности ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

К окружности с центром в точке О проведены касательная АВ и секущая АО?

К окружности с центром в точке О проведены касательная АВ и секущая АО.

Найдите радиус окружности, если АВ = 12 см, АО = 13 см.

Видео:К окружности с центром в точке O проведены ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

К окружности с центром в точке О проведены касательная АВ и секущая АО?

К окружности с центром в точке О проведены касательная АВ и секущая АО.

Найдите радиус окружности, если АВ = 12см, АО = 13см.

Видео:Геометрия Из одной точки проведены к окружности две касательные, длина каждой из которых равна 12 смСкачать

К окружности с центром в точке О проведены касательная АВ и секущая АО?

К окружности с центром в точке О проведены касательная АВ и секущая АО.

Найдите радиус окружности, если АВ = 12см АО = 13см.

Видео:Геометрия Докажите, что если через точку A к окружности проведены касательная AM (M – точка касания)Скачать

К окружности с центром в точке О проведены касательная АВ и секущая АО?

К окружности с центром в точке О проведены касательная АВ и секущая АО.

Найдите радиус окружности, если АВ = 12, Ао = 13.

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Из точки А не лежащей на окружности, проведены к ней касательная и секущая?

Из точки А не лежащей на окружности, проведены к ней касательная и секущая.

Расстояние от точки А до точки касания равна 12 см, а до одной из точек перисичения секущейся окружностью равна 18 см .

Найдите радиус окружности если секущаяся удалена от ее центра на 3 см.

Видео:ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

К окружности с центром в точке O проведены касательная AB и секущая AO?

К окружности с центром в точке O проведены касательная AB и секущая AO.

Найдите радиус окружности, если AB = 12см, AO = 13 см.

Видео:ОГЭ 2021 Задание 16Скачать

К окружности с центром в точке О проведены касательная АВ и секущая АО?

К окружности с центром в точке О проведены касательная АВ и секущая АО.

Найдите радиус окружности, если АВ = 14, АО = 50.

Если вам необходимо получить ответ на вопрос ПОМОГИТЕ ПЛИЗ К окружности с центром в точке о проведены касательная ав и секущая ао Найдите радиус окружности, если AB = 12 см, AO = 13 см?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Рисунок 3, основание это радиус круга, соответственно диаметр равен 4, а высота 3 она же образующая.

5 + 5 + 7 = 17 (см) ₽ 5 + 5 + 5 = 15(СМ) ₽.

Рассмотрим BKC, КЕ биссектриса т. Е делит угол пополам значит ВКЕ = СКЕ.

Ответ : |BC| = a = 2√3. |2AO + 2CO| = 4. |AС — (3 / 2) * ОС| = 3. Объяснение : В равностороннем треугольнике центр описанной окружности лежит на пересечении высот треугольника, которые являются и биссектрисами и медианами. АО — радиус описанной о..

Привет, BD — выстота = >BDC = 90° найдем угол DBC = 180 — (90 + 42) = 48° Треугольники авd и abd равны = >ABD = 48 ABC = 48 + 48 = 96°.

Пусть A1 — начало координат Ось X — A1B Ось Y — A1D1 Ось Z — A1A A1D1 (0 ; 1 ; 0) M(1 ; 1 ; 0. 5) D(0 ; 1 ; 1) Уравнение A1MD ax + by + cz = 0 подставляем координаты точек a + b + 0. 5c = 0 b + c = 0 Пусть с = — 2 тогда b = 2 a = — 1 — x + 2y — 2z ..

Р = а + в + с (68 — 16) : 2 = 26(см) боковая сторона треугольника.

68 — 16 = 52приходится на две стороны, так как треугольник равнобедренный то стороны равные 52 : 2 = 26 боковая сторона.

36 : 2 = 18 — отрезок КВ 18 : 2 = 9 — отрезок МК.

1) Точки в пл. АДД1 : А , Д Д1 , А1 . Точки в пл. АВС : А , В , С , Д . 2) MS лежит в пл. АВСД МД в пл. АВСД и АА1Д1Д АВ в пл. АВСД и АА1В1В 3) АА1 , ВВ1 , СС1 , ДД1 перпендикулярны пл. АВСД 4) прямой АД параллельны пл. ВВ1С1С и А1В1С1Д1 5) ..

Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Касательная к окружности

О чем эта статья:

Видео:№645. Из концов диаметра АВ данной окружности проведены перпендикуляры АА1 и ВВ1 к касательнойСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:№671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекаетСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

🌟 Видео

№636. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиесяСкачать

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

8 класс, 32 урок, Касательная к окружностиСкачать