Используя единичную окружность найдите знак разности tg 145 tg 140

Алгебра | 10 — 11 классы

13. Используя единичную окружность, найдите знак разности : а) sin 255˚ – sin 115˚ ; б) cos 30˚ – ctg 30˚.

14. Найдите знак произведения, используя правило знаков по четвертям : а) cos 160˚ tg 250˚ ; б) tg ctg ; в) tg 1, 3 ctg (–1, 4) sin (–0, 9).

13. а) 255˚ — угол третьей координатной четверти, синус отрицателен.

115˚ — угол второй координатной четверти, синус положителен.

Б) 30˚ — угол первой координатной четверти, и косинус, и котангенс положительны.

При этом значение котангенса больше значения косинуса.

14. а) 160˚ — угол второй координатной четверти, и косинус, и тангенс отрицательны.

В) 1, 3 — в первой координатной четверти, знак положительный.

–1, 4 — в четвертой координатной четверти, котангенс отрицательный.

–0, 9 — в четвертой координатной четверти, синус отрицательный.

Видео:Формулы приведения - как их легко выучить!Скачать

Определите знак выражений sin 20 tg120 sin( — 45) cos 70 ctg 240 tg( — 130)?

Определите знак выражений sin 20 tg120 sin( — 45) cos 70 ctg 240 tg( — 130).

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Найдите : sin( — 60) ; cos( — 180) ; sin( — 90) ; ctg( — 45)?

Найдите : sin( — 60) ; cos( — 180) ; sin( — 90) ; ctg( — 45).

Видео:Вычисление значений тригонометрических функцийСкачать

Выразите А)cos a, tg a и ctg a через sin a б)sin a, tg a и ctg a через cos а в)sin a, cos а и ctg a через tg a г)sin a, cos а и tg a через ctg a?

Выразите А)cos a, tg a и ctg a через sin a б)sin a, tg a и ctg a через cos а в)sin a, cos а и ctg a через tg a г)sin a, cos а и tg a через ctg a.

Видео:9 класс. Алгебра. Определение тригонометрических функций. Свойства тригонометрических функций.Скачать

Sin ^ 2a + cos ^ 2a — sin ^ 2a + ctg ^ 2a * sin ^ 2a?

Sin ^ 2a + cos ^ 2a — sin ^ 2a + ctg ^ 2a * sin ^ 2a.

Видео:Функция. Множество значений функции. Практическая часть. 10 класс.Скачать

Определите знак произведения : cos 20 градусов sin 100 градусов tg 500 градусов cos 120 градусов sin ( — 50градусов ) ctg 200 градусов?

Определите знак произведения : cos 20 градусов sin 100 градусов tg 500 градусов cos 120 градусов sin ( — 50градусов ) ctg 200 градусов.

Видео:Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

Определите знак выражения cos 100 tg 250 sin 300 ctg 100?

Определите знак выражения cos 100 tg 250 sin 300 ctg 100.

Видео:Определить знак выражения cos123°tg231°sin312°. Как решить Самый простой метод решения ТригонометрияСкачать

Докажите тождество : а)sin⁴ α — cos⁴ α = sin² α — cos² α ; б)sin² b — cos² c = sin² c — cos² b ; в)ctg² d — cos² d = ctg² d — cos² d?

Докажите тождество : а)sin⁴ α — cos⁴ α = sin² α — cos² α ; б)sin² b — cos² c = sin² c — cos² b ; в)ctg² d — cos² d = ctg² d — cos² d.

Видео:9 класс, 15 урок, Определение числовой функции. Область определения, область значения функцииСкачать

Какой знак имеют : а) sin a б) cos a в) tg a г) ctg a, если а = 240?

Какой знак имеют : а) sin a б) cos a в) tg a г) ctg a, если а = 240.

Видео:Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать

Определить знак выражения a) sin 95°x cos 95° = б) cos 130° x sin 420° = в) tng 361° x ctg 203° =?

Определить знак выражения a) sin 95°x cos 95° = б) cos 130° x sin 420° = в) tng 361° x ctg 203° =.

Видео:Задача 6 №27922 ЕГЭ по математике. Урок 139Скачать

Определите знаки sin cos tg и ctg 2, 8?

Определите знаки sin cos tg и ctg 2, 8.

Если можно подробно ; ).

Перед вами страница с вопросом 13. Используя единичную окружность, найдите знак разности : а) sin 255˚ – sin 115˚ ; б) cos 30˚ – ctg 30˚?, который относится к категории Алгебра. Уровень сложности соответствует учебной программе для учащихся 10 — 11 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

1)√55 2) 2√7 = √(7 * 4) = √28. 3)7 = √49 4)2√13 = √(4 * 13) = √52. Теперь когда все цифры записаны в виде корня легко найти наибольшее, ведь корень из наибольшего числа дает наибольшее значение, значит верный ответ 1)√55.

(6 * 9 ^ x — 1 — 10) / (9 ^ 2x — 1 — 9)≤1 9 ^ (x — 1) = 9 ^ x / 9 Умножим числитель и знаменатель на 9 (6 * 9 ^ x — 90) / (9 ^ 2x — 81) — 1≤0 (6 * 9 ^ x — 90 — 9 ^ 2x + 81) / (9 ^ 2x — 81)≤0 (9 ^ 2x — 6 * 9 ^ x + 9) / (9 ^ 2x — 81)≥0 (9 ^ x — 3)² / (..

Lg(5 — x) = Lg4 ^ 3 — Lg8, Lg(5 — x) = Lg4 ^ 3 / 8, Lg(5 — x) = Lg8, 5 — x = 8, — x = 8 — 5, — x = 3, x = 3 / ( — 1) = — 3. Ответ : x = — 3.

Так как у нас корень чётной степени, следовательно подкоренное выражение не может быть отрицательным( параллельно учитываем , что знаменатель не должен равняться 0). Получаем : y + 3>0, y> — 3. Ответ : ( — 3 : + бесконечность). ( — 3) не входит в ..

Сама теорема звучит так : Вертикальные углы равны 2. 2 угол DOC и угол AOB вертикальны и угол DOA и уголCOB тоже равны Угол DOA и угол COB равны так как вертикальные следовательно они = 138 Угол DOC и Угол AOB равны 180 — 138 по теореме смеж углов =..

11. а)1)180 — 30 = 150 2 * 3 * sin150 = 6 * 0. 5 = 3 2)180 — 60 = 120 4 * √3 * sin120 = 4√3 * (√3 / 2) = 6 3)180 — 45 = 135 1, 7 * 2, 2 * sin135 = 3, 74 * (√2 / 2) = 1, 87√2 4)(4 / 3) * (3 / 4) * sin150 = 0. 5.

Область определения функции : Х ≠ — 7.

Решение приложено на фото .

28 / (v — 1) + 28 / (v + 1) = 3 28(v + 1) + 28(v — 1) = 3(v² — 1) 56v = 3v² — 3 3v² — 56v — 3 = 0 D = 3172 √D = √3172 = 2√793 v = 1 / 6[56 + 2√793] км / час v2 = 1 / 6[56 — 2√793].

Видео:100 тренировочных задач #150 / Решите неравенство |sinx|≥|cosx|Скачать

Знаки тригонометрических функций

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.

угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты y к координате x .

Обозначение: sin α = y ; cos α = x ; tg α = y : x .

Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:

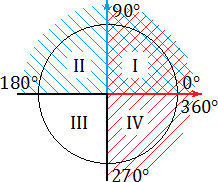
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:

1. sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата y ). А координата y будет положительной именно в I и II координатных четвертях;
2. cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;
3. tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x y II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;
4. cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) IV четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) II четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова II четверть, косинусы там отрицательны. Поэтому cos (5π/6) II координатная четверть, поэтому cos (2π/3) I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) II координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это IV координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
5. tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это II четверть, т.е. tg (3π/4) IV четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) III координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это I координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.

В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.

Задача. Найдите sin α, если sin 2 α = 0,64 и α ∈ [π/2; π].

Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.

Задача. Найдите cos α, если cos 2 α = 0,04 и α ∈ [π; 3π/2].

Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.

Задача. Найдите sin α, если sin 2 α = 0,25 и α ∈ [3π/2; 2π].

Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.

Задача. Найдите tg α, если tg 2 α = 9 и α ∈ [0; π/2].

Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!

💡 Видео

Разбор 36 вариантов Ященко. Вариант 11Скачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать

Текстовые задачи. Профильный ЕГЭ. Задание 10Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

ЕГЭ Математика Задание 6#27935Скачать