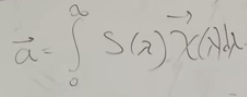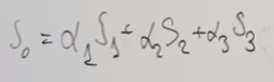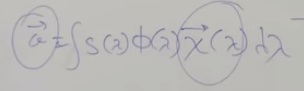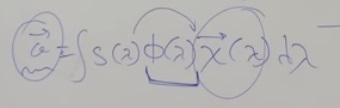Интерполяция цвета в треугольнике (5 видео)

Интерполяция цвета в треугольнике

Рассматривается частный случай растровой развертки полигона в окне вывода, когда известны цвета вершин этого полигона. Эти цвета могут быть либо заданы, либо рассчитаны с использованием некоторой модели освещенности.
Так, в 3ds Max полигону можно задать произвольной сложности материал, указать группу сглаживания, в сцене разместить источники света, задать параметры выбранной программы воспроизведения и пр. Далее приложение, а точнее отвечающий за воспроизведение плагин обеспечит расчет цветовых характеристик выводимых полигонов и их отображение в заданных видовых окнах или в окне программы воспроизведения (рис. 1).

Рис. 1. Модифицированная сфера

Для получения рис. 1 можно употребить, например, следующий код:

delete $*
mrbl = marble()
mrbl.coords.Tiling = [7, 7, 1]
std = standard showInViewport:true diffuseMap:mrbl
—meditmaterials[1] = std
sph = sphere radius:30 pos:[0, 0, 0] material:std segs:32 mapcoords:on
convertToPoly sph
move sph.verts[#] [0, 0, -37]
move sph.verts[#] [0, 0, -35]
move sph.verts[#] [0, 0, -33]
move sph.verts[#] [0, 0, -27]
move sph.verts[#] [0, 0, -20]
move sph.verts[#] [0, 0, -10]
move sph.verts[#] [0, 0, -5]
move sph.verts[#] [0, 0, -1]
rotate sph (eulerAngles 0 -15 0)
backgroundColor = gray
max quick render

При закраске Гуро рассчитываются RGB-компоненты цвета каждой вершины полигональной модели объекта. Эти значения используются затем для расчета RGB-компонентов при растровой развертке полигонов модели.
Значимым элементом модели освещенности являются нормали к полигонам (рис. 2), расчет которых в 3ds Max зависит от принадлежности полигона к той или иной группе сглаживания.

Рис. 2. Объект и его нормали

Нормали рассчитываются в каждой вершине полигона (рис. 3); полученные значения используются затем при расчете цвета вершины.

Рис. 3. Все полигоны в одной группе сглаживания: в каждой вершине по одной нормали

Иная картина будет, если полигоны входят в разные группы сглаживания (рис. 4).

Рис. 4. Групп сглаживания нет: в каждой вершине по 4 нормали

В приводимом далее материале полагается, что известны RGB-компоненты цветов в вершинах полигональной модели объекта и решается задача растровой развертки полигона с интерполяцией его вершинных цветов.
Рассматривается случай выпуклых полигонов.
При интерполяции цветов полагается, что используется прямоугольное проецирование, при котором 3d-точка P(X, Y, Z) отобразится на плоскости проекций в виде точки с координатами x, y:

Изображение выводится как растровый образ заданного размера, например 200*160 пикселей, создаваемый конструктором bitmap:

btmp = bitmap 200 160 color:white.

Замечание. Рассматриваемый подход является серьезным упрощением схемы преобразований координат, применяемой в графических приложениях.

Механизм интерполяции цветов проиллюстрируем на примере заливки отрезка, одна вершина которого имеет белый цвет, а другая — черный (рис. 5).

Рис. 5. К расчету R-компоненты цвета в точке Rc выводимого отрезка

fn drawLine p1 p2 prnt = (
l = line render_renderable:off wireColor:black parent:prnt
addNewSpline l
addKnot l 1 #corner #line p1
addKnot l 1 #corner #line p2
updateShape l
)
delete $*
r = 2; h = 40; d = 15; h7 = 0.7 * h
clr = white; clr2 = black
cl = cylinder radius:1 height:h wireColor:gray
sphere radius:r pos:[0, 0, 0] wireColor:clr parent:cl
sphere radius:r pos:[0, 0, h7] wireColor:gray parent:cl
sphere radius:r pos:[0, 0, h] wireColor:clr2 parent:cl
— Размерные линии
drawLine [0, 0, 0] [-d, 0, 0] cl
drawLine [0, 0, 0.7 * h] [-0.5 * d, 0, h7] cl
drawLine [0, 0, h] [-d, 0, h] cl
drawLine [-0.9 * d, 0, 0] [-0.9 * d, 0, h] cl
drawLine [-0.4 * d, 0, 0] [-0.4 * d, 0, h7] cl
rotate cl (eulerAngles 0 45 0)

Пусть R_a и R_b — значения R-компонент вершин отрезка (используется система цветов RGB).
Рассчитаем значение R-компоненты цвета произвольной точки C отрезка по формуле линейной интерполяции:

Rc = (1 — t) * Ra + t * Rb,

d_ab — длина выводимого отрезка;
d_ac — расстояние между А и С.
Последние значения рассчитываются по известным 3d-координатам точек А и С. В случае прямоугольного проецирования X и Y координаты точек А и С и их проекций совпадают.
Выведем для примера растровую развертку отрезка прямой, с толщиной по оси Х в 7 пикселей.
Заметим, что X-координата выводимого отрезка при увеличении Y на 1 изменяется на угловой коэффициент k (x = k * y + b). Поэтому очередная X-координата находится простым суммированием:

Используем для получения результата следующий код:

delete $*
— Создаем растровый образ
btmp = bitmap 300 150 color:brown
clrA = white
clrB = black
d = 20
d2 = d + 100
pa = [10, 10, 10]
pb = [290, 140, 100]
xa = pa[1]; ya = pa[2]; za = pa[3]
xb = pb[1]; yb = pb[2]; zb = pb[3]
dx = xb — xa; dy = yb — ya; dz = zb — za
if dy == 0 do messageBox «Error: dy = 0»
k = dx / dy
k2 = sqrt (k * k + 1)
dab = sqrt (dx * dx + dy * dy + dz * dz)
x = xa
y = floor ya
mLL = abs (floor dy)
for n = -3 to 3 do setPixels btmp [x + n, y] #(clrA)
dx = 0
dac = 0
for m = 1 to mLL do (
y += 1
x += k
dac += k2
t = dac / dab
clrC = (1 — t) * clrA + t * clrB
for n = -3 to 3 do setPixels btmp [x + n, y] #(clrC)
)
— Результат приведен на рис. 6 (используется физическая система координат)
display btmp

Рис. 6. Растровая развертка отрезка с интерполяцией цветов

dac = sqrt (dx * dx + m * m)

заменено на инкрементную схему:

k2 = sqrt (k * k + 1)
(dx = m * k, поэтому dac = m * k2, где значение m нарастает с шагом 1).

В качестве полигона используем четырехугольник (рис. 7), для отображения которого применен следующий код:

fn drawNGn d = (
nGn = line render_renderable:off render_displayRenderMesh:off
seed 2
addNewSpline nGn
addKnot nGn 1 #corner #line (random [0, 0, 0] [-d, d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [-d, -d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [d, -d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [d, d, 0])
close nGn 1
updateShape nGn
convertToPoly nGn
nGn.wireColor = gray
move nGn [d, d, 0]
return nGn
)
delete $*
nGn = drawNGn 60
arrClrs = #(white, yellow, black, [6, 135, 113])
vrts = nGn.verts
for k = 1 to 4 do sphere radius:3 wireColor:arrClrs[k] pos:vrts[k].pos

Рис. 6. Вершины полигона показаны в виде сфер (цвет сферы совпадает с цветом вершины)

Входными данными рассматриваемой задачи являются координаты вершин полигона и цвета вершин.
Выполним растровую развертку полигона, используя для расчета цветов пикселей известные цвета вершин, применив следующую последовательность действий:

Найти вершины pMi и pMa многоугольника с минимальной и максимальной Y-координатами.
y = pMi[2]
xL = pMi[1]; xR = xL;
— Цвета нижних вершин
clrAL = clrPMi; clrAR = clrAL, где clrPMi — цвет вершины pMi;
dacL = 0; dacR = 0
Найти вершины pL и pR, смежные с pMi (pL[1] 0.0): 1
default: 0
)
)
— Округление числа до целого значения
fn round x = (
fx = floor x
cx = ceil x
return if 0.5 * (fx + cx) > x then fx else cx
)
fn fndDab p1 p2 = (
dx = p2[1] — p1[1]
dy = p2[2] — p1[2]
dz = p2[3] — p1[3]
return sqrt (dx * dx + dy * dy + dz * dz)
)
— Этап stp заливки (интерполяционной развертки полигона)
fn oneStp yEI clrAL clrBL clrAR clrBR stp = (
while yI 0 do for x = xLI to xRI do (
setPixels btmp [x, yI] #(clr)
clr += dClr
)
)
)
fn fillInNGn nGn arrClrs = (
local k, m, pL, pR, pN, pE
nV = nGn.verts.count
arrVs = for k = 1 to nV collect nGn.verts[k].pos
arrVsY = copy arrVs #nomap
qsort arrVsY compareFNY
pMi = arrVsY[1]
pMa = arrVsY[nV]
y = pMi[2]
yI = round y
xL = pMi[1]
xR = xL
k = findItem arrVs pMi
pL = if k == 1 then arrVs[nV] else arrVs[k — 1]
pR = if k == nV then arrVs[1] else arrVs[k + 1]
if pL[1] > pR[1] do (
pT = pL
pL = pR
pR = pT
)
clrPMi = arrClrs[k]
clrAL = clrPMi
clrAR = clrPMi
clrBL = arrClrs[findItem arrVs pL]
clrBR = arrClrs[findItem arrVs pR]
kL = (xL — pL[1]) / (y — pL[2])
kR = (xR — pR[1]) / (y — pR[2])
kL2 = sqrt (kL * kL + 1)
kR2 = sqrt (kR * kR + 1)
dabL = fndDab pMi pL
dabR = fndDab pMi pR
dacL = 0
dacR = 0
for stp = 1 to nV do (
yE = amin pL[2] pR[2]
if yE == pL[2] then (
pE = pL
pN = pR
)
else (
pE = pR
pN = pL
)
— Очередной шаг растровой развертки полигона
oneStp (round yE) clrAL clrBL clrAR clrBR stp
if yE == pMa[2] do exit
m = findItem arrVs pE
pE1 = if m == 1 then arrVs[nV] else arrVs[m — 1]
pE2 = if m == nV then arrVs[1] else arrVs[m + 1]
pEN = if pE2[2] > pE1[2] then pE2 else pE1
— Угловой коэффициент kE линии между вершинами pE и pEN
kE = (pEN[1] — pE[1]) / (pEN[2] — pE[2])
kE2 = sqrt (kE * kE + 1)
clrBN = arrClrs[findItem arrVs pEN]
dabN = fndDab pE pEN
if pN == pL then (
pR = pEN
clrAR = clrBR
clrBR = clrBN
kR = kE
kR2 = kE2
dacR = 0
dabR = dabN
)
else (
pL = pEN
clrAL = clrBL
clrBL = clrBN
kL = kE
kL2 = kE2
dacL = 0
dabL = dabN
)
)
)
fn drawNGn d = (
nGn = line render_renderable:off render_displayRenderMesh:off
seed 2
addNewSpline nGn
addKnot nGn 1 #corner #line (random [0, 0, 0] [-d, d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [-d, -d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [d, -d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [d, d, 0])
close nGn 1
updateShape nGn
convertToPoly nGn
nGn.wireColor = gray
move nGn [d, d, 0]
return nGn
)
— Основная программа (поверка процедур интерполяционной заливки полигона)
delete $*
w = 200
h = 160
— Создаем растровую карту белого цвета
btmp = bitmap w h color:white
— Генерируем полигон (четырехугольник)
nGn = drawNGn 80
— Задаем цвета вершин четырехугольника
arrClrs = #(gray, yellow, black, brown)
—arrClrs = #(black, white, black, white)
—
vrts = nGn.verts
for k = 1 to 4 do sphere radius:3 wireColor:arrClrs[k] pos:vrts[k].pos
—
— Интерполяционная развертка многоугольника
fillInNGn nGn arrClrs
— Отображение результата (см. рис. 8)
display btmp

Рис. 8. Интерполяционная развертка полигона с наборами цветов вершин:
gray, yellow, black, brown и black, white, black, white

Та же, что и описанная выше схема, используется при закраске Гуро, с той разницей, что цвета вершин рассчитываются по правилам, определенным моделью освещения. Сами же модели создаются исходя о физических представлениях о природе света, свойств материала, влияющих на отражение, преломление и в ряде случаях на излучение света.

Содержание

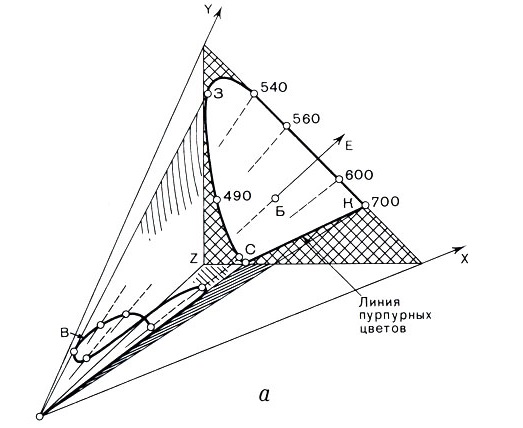
У цветового треугольника не два, а один угол
Простейшая модель цвета, в которой работал Шредингер
Окраска
Яркость
Насыщенность
Цветовой тон
Цветность
Метамерия
Фиолетовые окраски
Художник видит три цвета в точке, остальные — два
Баланс белого
Цветовой треугольник
Мондриан
Цветовое тело
Теорема Максимова
Задача цветовой сегментации
Фототехника
Мониторы
Краски для принтера
Lena512.tiff
Уроки по OpenGL с сайта OGLDev
Урок 09 — Интерполяция
Прямиком к коду!
🔍 Видео

Видео:4.1 Интерполяция кубическими сплайнамиСкачать

У цветового треугольника не два, а один угол

Как увидеть цвет, которого в природе не бывает?

Четыре года назад на Хабре был пост с интересным и полезным видео «Как устроен цвет». Лектор — Дмитрий Николаев, заведующий сектором зрительных систем ИППИ РАН.

Я сделал расшифровку (в меру своего понимания материала), потому что считаю и тему важной и подачу — отличнейшей. Пока набирал текст, чуть не поменял своё φ(λ). Слово спикеру:

Поговорим о математике и геометрии цвета, о том, какие абстрактные структуры заложены в этом слове.

Что такое «цвет» не знает никто.

Цвет — это что-то, о чем говорит человек, наблюдающий и познающий мир с помощью глаза.

Глаз регистрирует какие-то свойства электромагнитного излучения, называемого светом, попадающего в глаз, преломляющегося на хрусталике, проецируемого на сетчатку. «Колбочки» регистрируют какие-то мощностные свойства. И дальше внезапно человек говорит о каком-то «цвете».

В физике нет цвета, а есть спектральные свойства излучения.

«Цвет» связан с относительным распределением спектральной энергии, мощности или потока излучения. (При прохождении через призму человек видит характерную «радугу».)

Совершенно точно, «цвет» — психологический феномен. Цвет — это ощущение, к объективной физике не имеющий отношения.

Мы можем говорить о цвете вещей — красная рубашка — «краснота» рубашки напрямую никак не связана с тем, какое излучение придет от этой рубашки в глаз.

«Цвет» располагается на стыке трёх миров — биологии, физики, психологии.

Феномен цветопостоянства (цветовая константность) — способность человека, вне зависимости от того, что прилетело в глаз от конкретной точки объекта, оперировать термином «окраска объекта».

Не знаю ни одной системы технического зрения, которая обладает хорошей цветовой константностью (2014 год). Белый автомобиль освещенный красным закатным солнцем — техника ошибается, человек — нет.

Цвет есть свойство спектрального состава излучений. Общее всем излучением. в т. ч. и визуально неразличимым для человека.
— Шредингер

Это определение только половина правды. Если бы цвет соответствовал только излучению (а не к объектам в дополнение), то Шредингер был абсолютно прав.

Простейшая модель цвета, в которой работал Шредингер

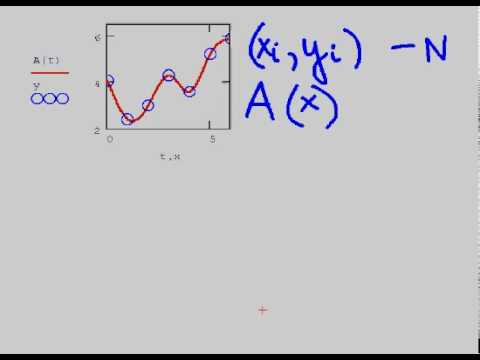
S(λ) — спектральное распределение светового потока. Мы говорим что этот цвет несет в себе фотоны с разными энергиями. Или это распределение электромагнитных волн с разными длинами волн.

X(λ) В глазу есть три типа «колбочек», каждый характеризуется спектром чувствительности, насколько много электронов выбивается из пигментов, которые находятся в этой клетке, в зависимости от того, какой фотон он поглотил. Это вектор.

Рассмотрим физически бесконечно малый участок сетчатки и скажем что в каждой точке у нас возникает три числа:

Каждый светочувствительный элемент суммирует все фотоны на разных длинах волн. В разных типах колбочек. Сколько-то электронов выбито в красном, сколько-то в синем, сколько-то в зеленом.

В реальности есть некоторые алгоритмы интерполяции, и в камере, и в человеке.

Как удалось понять что эта штука трёхмерная? Что у вектора «а» (электрически трудно вытащить) три компоненты? Днём. Ночью — одна, в сумерках — четыре. Но мы будем говорить о дневном зрении. Установить это удалось раньше, нежели разобрались с колбочками, с помощью колориметрических опытов.

Шредингер говорил о колориметрических условиях наблюдения. В поле зрения человека попадает только равномерно светящийся участок, как-будто человек смотрит в окуляр, и попадает только излучение определенного спектрального состава. При этом он может назвать цвет, который он видит. Но перечисление этих цветов ничего не скажет о размерности цветового пространства.

Был сделан следующий интересный эксперимент. Поле зрения человека было разделено на две области. В одну область подавался конкретный спектр. В другую половинку направляли смесь нескольких других источников. А человеку давали крутить столько ручек, смесь от скольки источников туда подавалась. И человека заставляли ответить на вопрос, может ли он выставить ручки так, чтобы он визуально не мог отличить границу между смесью и референтным излучением.

Выяснилось, что если предоставить человеку три ручки, то он всегда может уравнять любое излучение. И все другие испытуемые тоже не увидят границ. Двумя нельзя. Можно так подобрать две ручки и начальное базовое, что никаким способом не сможет.

Почему это работает с точки зрения нашего интеграла?

С учетом того, что наш интеграл — это линейная проекция из бесконечномерного пространства функций S.

Если у нас есть три некомпланарных вектора. Всегда есть разложение, причем все эти вещи неотрицательны.

Вот есть два окошка, где вы можете взвешенно суммировать, но не вычитать. Поэтому вместо того чтобы «вычитать» в одном окошке, мы «прибавляем» в другом. И всегда можно разложить на три базовых излучения.

Так было показано, что цветовое пространство внутри человека трёхмерно.

Это важный опыт. И никакое количество обнаруженных колбочек в человеческом глазе не может заменить этого опыта. Потому что обнаруженное число разных типов светочувствительных клеток в человеческом глазу может ограничить размерность этого пространства сверху. Если есть три типа колбочек, то цветовое пространство не выше трёх.

Дальтоникам достаточно две рукоятки. У них другое цветовое пространство. Поэтому неверно утверждать, что они «не видят» какого-то цвета. Для них некоторые пары наших цветов являются одним цветом. Причем таких пар бесконечно много. Но нет такого участка спектра, который они не различают.

«Зелёный и красный очень близко». Простейший лингвистический эксперимент: сколько вы можете цветов назвать между зелёным и синим, и между зелёным и красным.

Связано это с тем, что концентрация светочувствительных рецепторов в фовеальной области («зеленых» и «красных») — подавляющее большинство, а синих практически нет, они расположены на периферии. Поэтому человеческий глаз как прибор может очень точно, за счет усреднения многих колбочек оценить спектральный состав в области красно-зеленого, хотя сами детекторы показывают очень скореллированные сигналы, а сильно декореллированный синий сигнал теряет в точности из-за того, что он пространственно очень редок.

Дискомфорт от ярких синих надписей возникает из-за того, что мы воспринимаем их краем глаза, а краем глаза мы не любим смотреть.

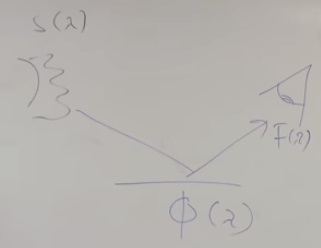
Основной недостаток определения Шрёдингера связан с тем, что он вообще игнорировал то, как человек «пользуется» цветом. Человек не смотрит на абстрактное излучение, он смотрит на цвет, который отражается от поверхности.

Я всё время буду для простоты полностью игнорировать геометрию, индикатрисы рассеяния, и буду говорить только об относительном спектральном составе. как мощность меняется, меня не будет большую часть времени беспокоить. Исчезнут все интегралы по телесным углам и много чего неприятного.

«Интеграл», который «прилетает» в глаз имеет такой вид:

Вот отсюда растут все цветовые ощущения.

Возвращаясь к эксперименту с одуванчиком, хочу сказать, что человеческое зрение решает феноменальную задачу, невообразимую. Если рассмотреть одну точку она очевидно неразрешима. Оцените.

Мы знаем вот эти три числа (векторы «а»), мы знаем в результате самокалибровки вот эти три функции X(h). Мы НЕ знаем как устроено солнце, оно всегда разное, на закате, в зените, в зависимости от облаков, лампы разноцветные.

Задача цветового зрения человека оценить вот эту функцию:

Эта функция задает материал. Эта функция говорит, спелый фрукт или нет. Эту функцию мы хотим определить по трем числам, при условии, что она домножилась на другую неизвестную функцию.

Пока мы не оценили, как/чем был освещен объект, мы ничего не можем сказать о цвете. Если бы этот механизм не работал, мы бы путались, если бы нам показывали красную бумажку, освещенную белым цветом и белую бумажку, освещенную красным цветом. А мы не путаемся. До тех пор, пока в поле зрения более чем только эта бумажка. Если бумажка висит в пустоте — мы не можем различить. Если объектов много то сразу понятно, какого цвета освещение, какого бумага.

Мозг решает кучу задач, о которых мы не догадываемся, пока не приходится запрограммировать робота, тогда начинаешь понимать сколько всего делает зрительная система человека.

Окраска

Выделим это понятие из слова «цвет». Окраска — объективная характеристика физического предмета. Даже если я закрываю глаза, окраска не исчезает, она присуща самому предмету, в отличие от «цвета», который есть ощущение.

Яркость

Существуют черно-белые телевизоры и цвет можно почти «изжить». Остается мощностная компонента цвета. Нужно разделять слова «яркость» и «светлота». Яркость относится к излучению, а светлота — к объекту. Объект может быть светлым, а освещение — ярким. И то и другое — мощностные характеристики, но принадлежат разным мирам и это важно. Коэффициент отражения зажет между 0 и 1, а мощность излучения сверху ничем не ограничена.

Белый объект в черно-белом мире существует, а «белого» (максимально яркого освещения) излучения не существует.

Насыщенность

Существует параметр, естественно объясняемый человеку. Насыщенность — насколько цвет далёк от серой шкалы. Насыщенность — это то, что уменьшается при разбавлении любым серым цветом. Максимальная насыщенность у излучения лазера. (Чуть позже поговорим про химические психоактивные вещества.)

Цветовой тон

Это то, что остается от цвета в цветовом пространстве, после того, как мы ввели две предыдущие координаты. Иногда мы путаем цвет и цветовой тон. Этому есть и физические и биологические предпосылки.

Цветность

Это та двухкомпонентная часть цвета, которая не мощностная. Если из цвета излучения «выкинуть» «яркость», то останется «цветность».

Метамерия

В отличие от любой женщины, мужчина напрочь игнорирует явление метамерии. Каждая девушка знает, что не стоит покупать кофточку, которая подходит к юбке под люминесцентном свете, пока не протестировал это при естественном освещении. Это интуитивное знание о существовании метамерии окраски.

Метамерия излучения — это когда мы знаем, что существует бесконечно много разных спектров, которые могут попасть на глаз, чтобы у человека появилось одинаковое ощущение.

Цвет (по Шредингеру) — это то общее у всех спектров, которые вызывают одно и то же ощущение.

Метамерия окрасок. Если две разные окраски выглядят одинаково при некотором фиксированном S, отсюда никак не следует, что при другом S они будут совпадать.

Гарантировать что они будут совпадать, мы можем только для одинаковых φ, то есть для абсолютно одинаковых спектров. Мы можем подобрать такие отвратительные спектры источников, полосные например, с какими-то пиками, что две окраски, которые только что казались одного цвета станут разными. И вот это как раз и происходит в магазинах.

Три четверти задачи цветовой константности — это оценить S(λ) в той точке, где находится объект, то есть оценить как он был освещен. После этого мы получаем историю, похожую на колориметрические условия наблюдения.

На западе широко используются линейные модели. Выберем три таких спектра, что любая окраска может быть приближена к линейной комбинации этих трёх базовых окрасок. И получаем связь параметров окраски через матрицу 3х3. Всё становится красиво, есть куча алгоритмов, правда работают они очень плохо. Есть глубокая причина.

И примитивная причина — вы не можете различные узкополосные спектры одновременно хорошо аппроксимировать суммой трёх любых.

Если есть узкий пик, который непрерывно катается по шкале длин волн, то линейная модель не может все эти узкие спектры одновременно хорошо аппроксимировать.

Существует ли модель, которая умеет это делать? Да, существует. Гауссовская модель.

Мы считаем, что φ(λ) — это экспонента от полинома второй степени. У неё три параметра. Она умеет аппроксимировать белый, она легко апрроксимирует любой узкий спектр, но серию «колокольчиков» она уже не сможет.

Цвета и высокой и низкой насыщенности гауссовская модель аппроксимирует одинаково хорошо. Это очень важное её свойство. Второе свойство:

В нашем интеграле функции между собой перемножаются. Для того, чтобы параметры модели никуда не ускакивали, важно, чтобы модель была замкнута относительно операции умножение.

Фиолетовые окраски

Есть одно «но». Есть фиолетовые окраски, они имеют такой спектр — сильно не ноль в красной области и сильно не ноль в синей области и гауссиана с этим не может работать. Но есть трюк.

Если под экспонентой стоит полином с ненулевым квадратичным коэффициентом, у нас гауссиана превращается в экспоненциальную растущую параболу. И интеграл от нуля до бесконечности перестает быть конечным, но, поскольку мы всегда наблюдаем это через глаз, где гауссианы успевают убывать быстрее, для этого у них старший коэффициент должен быть по модулю больше чем у этой окраски, то оказывается, что интеграл в результате берется, и мы можем спокойно работать с не очень насыщенным фиолетовыми окрасками и фиолетовыми излучениями.

Как оценить спектр источника излучения? Если мы это сделаем, то дальше, введя цветовую модель, мы решим задачу цветовой константности. Существует несколько гипотез на этот счет. Наиболее ранние модели были такие: если человек видит в сцене белый объект или если он видит блик (на гладкой диэлектрической поверхности видит отражение источника).

Вне зависимости от цвета самого объекта блик несет спектр цвета источника. Там не происходит «умножения» на окраску.

Все окрашенные диэлектрические поверхности в первом приближении могут быть описаны диэлектрической моделью блика Шеффера, когда есть зеркальное отражение, например, от пота на лбу, и есть рассеянное отражение от частиц пигмента «в глубине».

«Зеркальная компонента» — как если бы от белого объекта. В блике любой диэлектрик выглядит как белый. С металлами не так. Гладкий металл отражает «своим» цветом. Блик от золота всегда желтый. Блик от меди всегда красный.

Художник видит три цвета в точке, остальные — два

Ещё одна вещь, которая осложняет понятие «цвет», связана с тем, что когда мы смотрим в одну точку, мы видим сразу три цвета. Первое что мы «видим» (можем научиться видеть) — это «что же оттуда прилетело». Чтобы хорошо это видеть, нужна трубочка. Если человек не видит «что прилетело», он не сможет стать художником-реалистом. Много трюков и много самотренировки требуется художнику, чтобы понять, что из какой точки прилетело и нарисовать именно «это». Тогда картина будет реалистичной. Вместо этого мозг решает полезные задачи (поскольку быть художником абсолютно бесполезно в гонке за выживание). Мозг определят что туда «упало». Глядя на улицу, мы понимаем, что трава освещена закатным солнцем. Тень голубовата, потому что освещена небом. И одновременно вы видите в этой точке какого цвета объект. Глядя на человеческое лицо вы увидите мельчайший румянец, потому что это эволюционно чрезвычайно важно (зарумянилась девушка или нет), но при этом вам все равно, как падают тени на её лицо, освещена она закатом или полуденным солнцем, или это облачное небо. Проблема в том, что не художник видит это одновременно два цвета, не отдавая себе отчет в этом, а художник должен видеть три цвета.

Когда мы рисуем то, что мы видим, в смысле окрасок, мы начинаем рисовать как дети. А художнику приходится отключать очень много алгоритмов зрения, чтобы превратиться в «фотоаппарат».

Баланс белого

«Баланс белого» в фотоаппаратах не значит вообще ничего. Это шаманство. Как в кулинарных книгах — «варить до готовности», «добавьте соли и перца». Для фотографа это имеет смысл, они знают что будет меняться, если эту рукоятку повернуть, но на самом деле абсолютно не понятно что это такое. Я догадываюсь что там происходит, но это хуже чем о цвете говорить. Я бы предпочел не говорить о «балансе белого», надо держаться твердой почвы.

Цветовой треугольник

У нас есть некоторое трёхмерное цветовое пространство в котором живут наши вектора , условно назовём его RGB, чтобы компьютерщикам было легче. И Вернулись к излучениям. Кто-то светит в глаз.

Вопрос: Любые ли комбинации R, G и B возможны?
Ответ: Конечно же, нет.

Мы рисовали спектры чувствительности. Они частично пересекаются. Они нигде не строго ноль, там где другие не ноль. Это значит, что вы не можете возбудить одну колбочку, не возбудив, хотя бы немного, колбочку другого типа.

Если бы мы могли освещать «спектром с отрицательной энергией», то мы могли бы в любую точку пространства, включая и отрицательные, зайти.

Если осветим вот так, всё будет хорошо, но это физически невозможно.

Математически можно сказать вот что: Всевозможные спектры излучений в исходном бесконечномерном пространстве образуют конус (не «круглый», а из линейной алгебры).

Конус — это такая структура, что если вектор принадлежит конусу, то вектор умноженный на неотрицательное число тоже принадлежит конусу.

Неотрицательные функции одного аргумента, которыми мы бомбардируем наш глаз — они образуют конус.

Представьте бесконечномерный куб и тот «квадрант», где все оси положительные, там и будет жить наш конус.

Поскольку наш глаз осуществляет линейную проекцию а пространство RGB, то здесь, в цветовом пространстве, все допустимые реакции тоже будут образовывать конус. Более того — выпуклый конус. Это значит что сумма двух векторов конуса с неотрицательными коэффициентами так же принадлежат конусу.

Построим сечение и сделаем центральную проекцию. Плоскость цветности мы можем ввести как угодно. Из нуля растет яркость.

На плоскости цветности, раз это конус, у нас должна быть какая-то выпуклая фигура.

То что эта штука называется треугольником — это отдельный юмор. У неё два угла. Но я вас сейчас с лёгкостью докажу, что на самом деле у цветового треугольника должен быть один угол. И это очевидно. Почему их два — совершенно не понятно.

Вспомнив, как устроены функции, и что это выпуклое множество, мы можем сказать, что любую функцию можно собрать из выпуклой суммы дельта-функций.

Математики меня бы убили за такую вещь, но… в пределе. Что бы это ни значило.

Давайте возьмем такую мелкую-мелкую дискретизацию и скажем, что любая функция в пределах этой дискретизации — это сумма каких-то столбиков. Это значит, что любой спектр, который может попасть нам в глаз — это выпуклая комбинация каких-то лазерных излучений, бесконечно узких. Это значит, что весь цветовой конус — это выпуклая оболочка реакций на лазерное излучение. С цветовым треугольником то же самое. ЦТ- это на плоскости цветности выпуклая оболочка лазерных излучений.

Начнем двигаться лазером из ультрафиолетового в инфракрасный. в цветовом пространстве мы обойдем какую-то петлю.

Почему петлю? Из нуля уйдем и в ноль вернемся.

Потому что на УФ не реагируем, на ИК тоже не реагируем.

Какая-то произвольная траектория.

Человек специфическим образом устроен, что здесь нет вогнутостей:

Это петля. У неё один единственный «клюв». И мы эту штуку гладко проецируем на плоскость. И у неё должен быть один «клюв». Это очевидно. В остальных местах всё непрерывно.

Дело в том что этот излом находится непосредственно в центре центральной проекции. А производные с двух разных сторон — разные.

Это не «клюв», который сходится к одной касательной, касательная справа и касательная слева — разные.

Поэтому УФ часть «клюва» проецируется сюда:

А все лазерные излучения живут вот здесь:

И каждой части этой дуги цветового треугольника приписать какую-то длину волны.

А вот этой штуке нельзя приписать никакие длины волн:

Потому что здесь замыкается выпуклая оболочка. Таких лазеров не бывает. Это можно возбудить только двумя дельта функциями минимум.

Цветовой треугольник — это выпуклая оболочка над реакциями на лазерное излучение.

Не все точки нашего RGB достижимы в принципе, по физике. Есть, как я говорил, трюк. Можно очень сильно дать человеку по голове, либо принять каких-либо веществ. Что для мозга то же самое. Если у нас уже на этапе обработки будут возникать удивительные числа, то там они могут возникать такие, которых в природе не бывает. С колбочки такого прийти не могло. Но в зрительной коре, под воздействием какой-то химии или механики, такие комбинации возникнуть могут. Или во сне. Во сне же мы получаем сигналы не от колбочек. В принципе, мы можем видеть цвета, которых в природе не бывает.

Вопрос: А в воображении можем?
Ответ: Я ничего не могу сказать про ваше воображение, простите. Будучи абсолютно честным, я даже про ваше существование ничего не могу сказать, а вы про воображение просите.

Мондриан

Был такой художник — Пит Мондриан. С Кандинским и Малевичем считается отцом абстрактной живописи.

У Мондриана есть характерные картины из прямоугольников нескольких цветов.

В цветоведении «мондриан» стал нарицательным, потому что это очень хороший воображаемый объект, наблюдая за реакцией человека, который смотрит на «мондриан» можно много сказать про зрительную систему. Меняя цвета на картине и меняя освещенность можно что-то понять про человека. Например, поняли, что если на картине есть белый, то человек не путает освещение с окраской, если белого нет, то может путать.

Если взять мондриан, который не бликует, очень матовый, и его осветить равномерно, а потом мы будем менять всевозможные окраски на мондриане. Что в цветовом пространстве (при фиксированном Х(глазе) и S(источнике)) «высечет».

Некоторые фотоаппараты фотографируют ИК сигнал от пульта телевизора — синим. И это только меньшее зло. На самом деле цветопередача любого фотоаппарата отвратительная. Но интерпретационная мощь человеческого зрительного аппарата настолько велика, что мы на это забиваем.

Человек насыщенные цвета любит больше, поэтому у телевизоров насыщенность задрана. Чтоб человек предпочитал телевизор смотреть а не в окошко. В окошке — серо и отвратительно, в телевизоре — прекрасно.

Цветовое тело

Фиксированно Х, фиксированно S, меняем φ, но оно зажато от 0 до 1.

Кроме черной точки:

есть белая точка:

Когда φ строго равен 1. Белый объект, всё отражает (если источник желтый, то «желтая точка»). За пределы этой точки мы уже не выйдем. Это уже не конус. Что же это?

Это выпуклая симметричная фигура, чечевицеобразная.

Почему эта штука симметрична? Это просто. На любой спектр окраски найдется другой, такой, что это единица минус первый спектр.

Теорема Максимова

Если вы знаете форму цветового тела, вы можете восстановить спектр S(λ) для всех λ. Для меня это просто шок. К несчастью, это не может быть хорошим алгоритмом цветовой константности, потому что никогда не бывает настолько много цветов, которые наблюдает человек, и они все по-разному освещены по мощности.

Солнце похоже на недокаленную лампочку(желтая), а небо, наоборот, — на перекаленную лампочку (голубая). Это к вопросу про цветовую температуру. Начали аппроксимировать источники света планковскими источниками. А у планковского источника есть соответствующая температура. До какой температуры надо абсолютно черное тело нагреть, чтобы оно такой спектр выдало из себя.

Я могу взять всевозможные:

для каждого планковского источника, которых всего однопараметрическое семейство, я могу построить цветовое тело, я могу спроецировать это цветовое тело на плоскость цветности, и оно займет не весь цветовой треугольник. Если я вижу в сцене что-то что выпадает за эту проекцию, я могу исключить этот источник из списка гипотез о том, чем это было освещено.

На западе это называется алгоритм gamut. Как применять теорему Максимова непонятно, потому что цветовое тело мы можем наблюдать только в лаборатории.

Задача цветовой сегментации

Есть более простая задача, чем задача цветовой константности. Вопрос, можем ли мы, глядя на фотографию, определить где кончается один цвет и начинается другой. Не называя цвета. Сказать — здесь скачок окраски.

Будем считать, что у нас нет текстур и акварелей. Однородные объекты, а между собой разные, они собой делят пространство и есть области с разной окраской. Разбиение изображения на эти области — это задача цветовой сегментации.

Много лет люди наступают на одни и те же грабли. Люди говорят: «Я же вижу что весь стол коричневый, значит, и программа должна это видеть.» Нужно просто покластеризовать цветовое распределение хорошим алгоритмом. Не работает. И никогда не заработает. Поскольку исходная посылка была ложной. То, что мы видим как объект одного цвета, в цветовом пространстве никак точкой саппроксимированно быть не может. В большинстве случаев. Если это равномерно освещенный мондриан, то да.

Представим идеального сферического коня в вакууме. Определенного цвета. Вот он висит и освещен бесконечно далёким солнцем. Сбоку. Вопрос: как будет проецироваться этот конь в цветовое пространство?

Ответ. В отличие от плоского коня, сферический конь в цветовом пространстве будет подмножеством прямой, проходящей через начало координат.

С этой штукой k-means не справится. И большая часть вещей выглядит так. А если сфера была ещё и гладкой, а не матовой, то возникает блик и у нас индикатрисса рассеяния имеет два члена, тогда у нас под интегралом будет взвешенная сумма двух цветов, и вот это штука станет кусочком плоскости, проходящей через ноль.

Можно показать, что в разных простейших случаях наблюдения различных объектов и разных условиях освещения, однородно окрашенные объекты будут проецироваться в цветовое пространство как линейные подмногообразия. Не обязательно через ноль проходят.

Можно ввести ранговую классификацию: иногда это будут точки, иногда — плоскости, который проходят через ахроматическую прямую. И по описанию сцены, утверждая, был ли белый источник, был ли объект гладким, или что источников было два, причем один параллельный а другой диффузный (как небо, со всех сторон), можно понять не только размерность этого подмногообразия, но и его положение относительно нуля и ахроматической прямой.

Оказывается, что это важно, потому что мы можем тогда сказать, как эта штука проецируется на плоскость цветности, потому то если это линейное подпространство, то она теряет в размерности при проекции на цветовой треугольник, что хорошо. А если мы спроецируем, то что мы видим на окружность цветового тона, то окажется, что во многих случаях, когда даже если это была плоскость, она на ЦТ стала прямой, проходящей через серую точку, а потому она спроецировалась в одну точку на окружности цветового тона. И вот это очень важно.

Человек потому и выделяет цветовой тон как отдельную координату в цветовом пространстве, потому то это наиболее стабильная компонента цвета при изменениях освещения и наблюдения.

В нашем цветовом пространстве есть ахроматическая прямая, куда проецируются спектры равные константе

Фототехника

У фотоаппарата спектры чувствительности должны быть линейной комбинацией человеческих, тогда ему достаточно трёх светочувствительных элементов, но поскольку это не так, то нужно больше, а делают три и не сводимых к человеку, поэтому у аппарата цветопередача далека от идеальной.

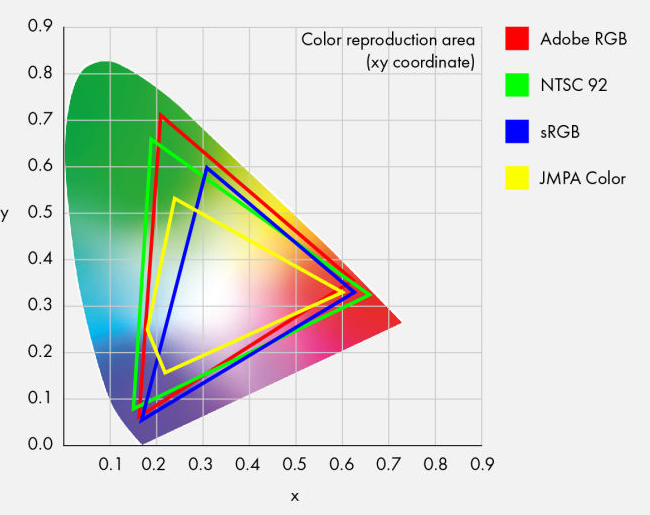
Мониторы

Интересно, что про мониторы ответ совершенно другой. Хороший монитор должен иметь как минимум пять типов источников света. Монитор может только выпуклую комбинацию своих трёх цветов изображать, а это всегда подмножество истинного ЦТ человека. Чтобы хорошо его саппроксимировать нужно взять еще несколько фильтров и пятиугольником аппроксимировать. В Америке есть одна фирма, которая планирует рано или поздно сыграть на этом.

Краски для принтера

Из-за метамерии окрасок, красок у принтера должно быть бесконечно много. Иначе не будет такого, что при разных источниках цвета картинка всё равно выглядит правильно. Это одна из причин, почему у профессиональных принтеров количество красок достаточно велико. И постоянно выпускают «патчи», которые улучшают метамерию при наблюдении в люминисцентном свете.

Lena512.tiff

C 1973 года в индустрии обработки изображений принято новые алгоритмы испытывать на изображении:

Вот тут даже разыскали эту «Лену».

У самих специалистов-тестировщиков изображение ниже простирается гораздо дальше. Я вот и подумал, почему бы цветоведам не придумать свою шутки и девушка в мандриане может стать стандартом.

Видео:Графика с нуля | Растеризация треугольника, интерполяцияСкачать

Уроки по OpenGL с сайта OGLDev

Видео:Интерполяция. ТемаСкачать

Урок 09 — Интерполяция

В этом уроке демонстрируется важная часть 3D конвейера — интерполяция, которую растеризатор через переменные выводит из вершинного шейдера. Как вы уже заметили, чтобы получить на экране какие-либо объекты, необходимо назвать и задать одну из переменных вершинного шейдера как ‘gl_Position’. Это 4-вектор, содержащий однородные координаты вершин. XYZ компоненты вектора делятся на W элемент (процесс, называемый нахождением перспективы (perspective divide) и рассматривается в уроке, посвященной этой теме) и любые элементы, выходящие за размеры окна ([-1,1] для XY; [0,1] для Z) будут обрезаны. Результат преобразуется в координаты пространства экрана и затем треугольник (или любой другой примитив) рендерится на экран растеризатором.

Растеризатор выполняет интерполяцию между тремя вершинами треугольника (или проходя от строки к строке или каким-то другим способом) и «посещает» каждый пиксель внутри треугольника запуская для него фрагментный шейдер. От пиксельного шейдера ожидается цвет пикселя, который растеризатор помещает в буфер цвета для отображения (не считая несколько дополнительных проверок типа теста глубины и т.д.). Любые другие данные, выходящие из вершинного шейдера не проходят эти этапы. Если фрагментный шейдер не требует переменную явно (а вы можете смешивать и сочетать несколько пиксельных шейдеров с одним и тем же вершинным), тогда драйвер оптимизации отбросит любые ее упоминания в вершинном (но только для данной комбинации шейдеров). А если фрагментный шейдер использует эту переменную, то растеризатор интерполирует ее во время растеризации и каждый вызов пиксельного шейдера будет получать свое интерполированное значение в соответствии с его позицией. Обычно это означает, что числа для пикселя, который немного правее, будут слегка различаться (хотя чем дальше треугольник от камеры, тем различия все меньше).

Две вещи, которым необходима интерполяция — это нормали для треугольника и координаты текстуры. Нормаль у вершины чаще подсчитывается как среднее между всеми нормалями у треугольников, которые содержат эту вершину. Если объект не полностью плоский, то обычно это значит, что все 3 нормали вершин одного треугольника будут отличаться друг от друга. В этом случае мы полагаемся на интерполяцию для расчетов освещения, чтобы получить более реалистичные эффекты света. Случай координат текстур аналогичен. Эти координаты — часть модели, и они указываются для каждой вершины. Для «покрытия» треугольника текстурой, необходимо выполнить одинаковые операции для каждого пикселя и указать правильные координаты текстуры для этого пикселя. Эти координаты и есть результат интерполяции.

В этом уроке мы увидим эффект интерполяции с помощью раскрашивания стороны треугольника различными цветами. Из-за моей лень, цвет мы генерируем в вершинном шейдере. Более утомительным способом является предоставление данных буфером вершин. Обычно не требуется поставлять цвет из вершинного буфера. Мы передаем координаты текстуры и цвет из нее. После этот цвет участвует в расчетах света.

Видео:4.2 Интерполяция многочленом НьютонаСкачать

Прямиком к коду!

Переменные, передающиеся между этапами конвейера должны быть глобальными, а так же объявлены с ключевым словом ‘out’. Цвет — это 4-й вектор, первые 3 элемента которого RGB значения (соответственно) и W это альфа значение (прозрачность пикселя).

Цвета в графическом конвейере обычно представлены в виде вещественных чисел в отрезке [0.0, 1.0]. Позже эти числа будут переведены в целочисленные от 0 до 255 для каждого канала цвета (всего 16M оттенков). Мы устанавливаем цвет вершины как функцию от ее позиции. Сначала мы используем заготовленную функцию clamp(), которая проверит, не выходят ли наши значения из промежутка 0.0-1.0. Мы делаем это потому, что нижняя левая вершина треугольника имеет координаты -1,-1. Если взять значения как есть, то они будут интерполированы растеризатором, и пока и X и Y равны 0 мы ничего не увидим, потому что любые значения меньше либо равные 0 будут рендерится черными. Это значит, что половина стороны во всех направлениях будет черной до тех пор, пока цвет не дойдет до 0 и после станут чем-то другим. С помощью ограничения мы сделали только нижнюю левую вершину черной, дальше цвет быстро будет набирать яркость. Поэкспериментируйте с функцией clamp — удалите ее совсем или измените параметры, что бы увидеть эффект.

Результат функции clamp не сразу переходит в выходную переменную, поскольку она 4-вектор, а позиция — 3-вектор (clamp не изменяет количество элементов, только их значения). В GLSL не существует такого конвейера по умолчанию, поэтому мы должны сделать это явно. Для этого мы используем обозначение ‘vec4(vec3, W)’, которое создает 4-вектор объединением 3-вектора с полученным числом W. В нашем случае мы используем 1.0 чтобы пиксель был полностью непрозрачным.

Противоположный выходному цвету в VS входящий цвет в FS. Эта переменная претерпевает интерполяцию растеризатором, поэтому каждый FS будет (возможно) выдавать разный цвет.

Мы используем интерполяционный цвет в качестве цвета пикселя без каких-либо изменений и на этом завершаем этот урок.