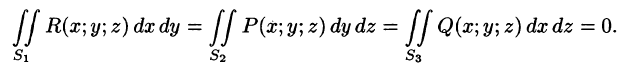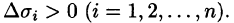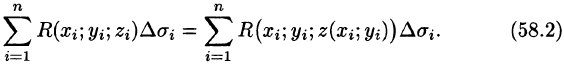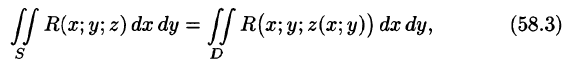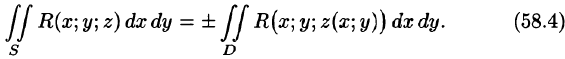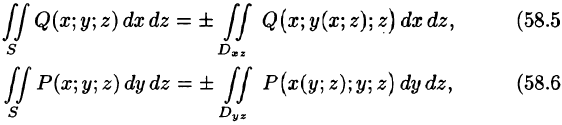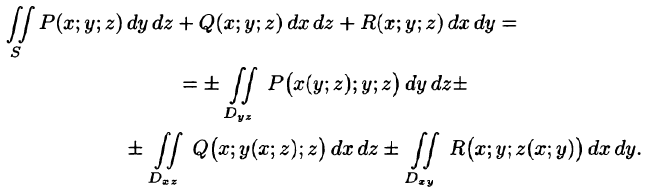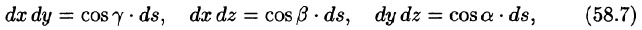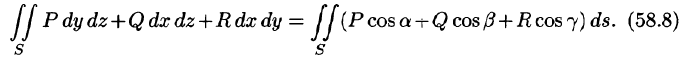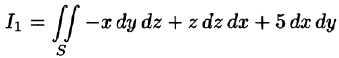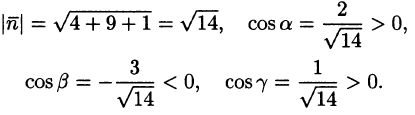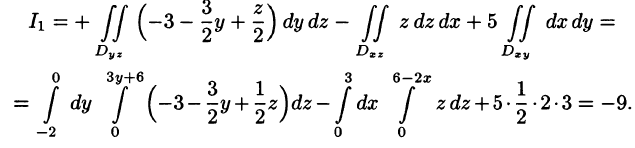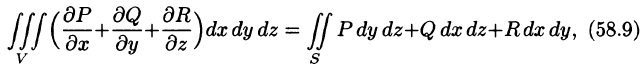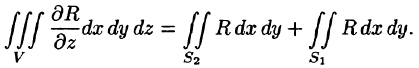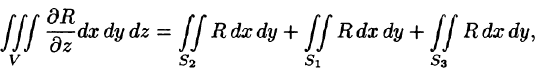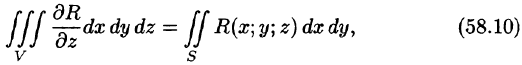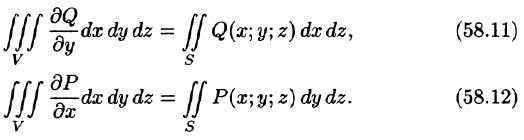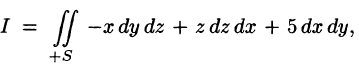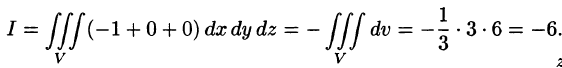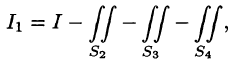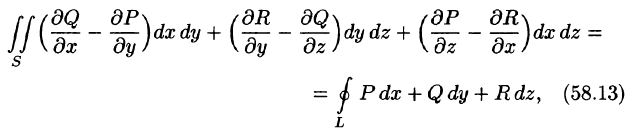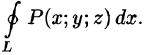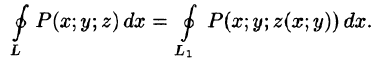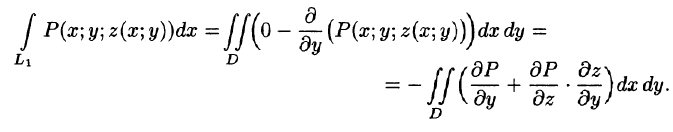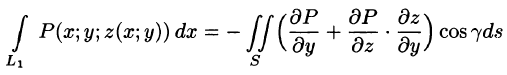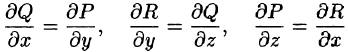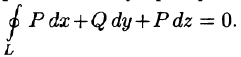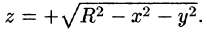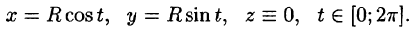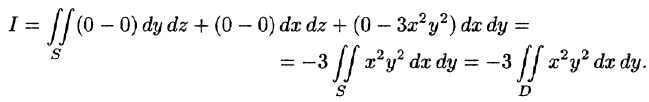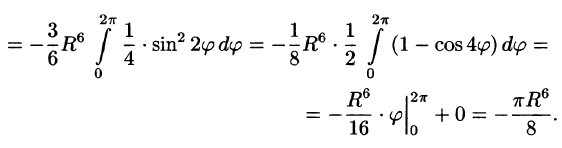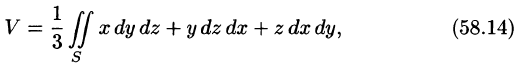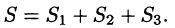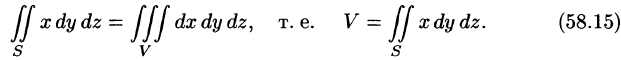Определение. Если функция определена на кусочно-гладкой кривой L и точки этой кривой разбивают ее на n элементарных дуг, в каждой из которых выбрана точка то , называется интегралом от f(z) по кривой L и обозначается или, в случае замкнутого контура L .
Если функция непрерывна на L, то интеграл существует (его часто называют контурным):
являются криволинейными интегралами от функций двух действительных переменных.
Если кривая L задана параметрическими уравнениями:
и каждая из этих функций гладкая, то
Известно, что вместо двух вещественных параметрических уравнений линии L можно ввести одно эквивалентное им комплексно-параметрическое уравнение
тогда уравнение (2.35) можно переписать так:
Формула (2.36) удобна для вычисления контурных интегралов.
Теорема 1 (основная теорема Коши). Если функция f(z) аналитична в односвязной области, то для любого кусочно-гладкого замкнутого контура L, лежащего в этой области,
Следствие. Если функция f(z) аналитична в односвязной замкнутой области, ограниченной кривой L, то
Заметим, что из теоремы Коши следует: если функция f(z) аналитична в односвязной области D, то для любой незамкнутой кривой L, принадлежащей D, интеграл от f(x) по L зависит только от начальной точки z0 и конечной точки z, т.е. от формы кривой (пути) L не зависит. При этом:
где F(z) – одна из первообразных функций для f(z), т.е. F’(z) = f(z). Формула (2.37) называется формулой Ньютона-Лейбница.
Теорема 2. Если функция f(z) аналитична в замкнутой области (односвязной или многосвязной) и L – граница D, то для любой точки z0, лежащей внутри этой области, справедливы следующие формулы:
Интеграл в правой части формулы (2.39) называется интегралом Коши для функции f(z), а сама эта формула носит название интегральной формулы Коши.
Формулу (2.39) часто называют интегральной формулой Коши для n-й производной функции f(z), и она выражает тот факт, что аналитическая функция, заданная в замкнутой области , дифференцируема сколько угодно раз в каждой точке z области D (следовательно, производные f’(z), f’’(z),,… аналитичны в точке z).
Отметим, что формула (2.39) получается из интегральной формулы Коши (2.38) в результате последовательного дифференцирования n раз по z0 под знаком интеграла.
Вычислить контурный интеграл где L – прямолинейный отрезок, соединяющий точку z = 0 с точкой z = 3+7i.
1) Сделаем схематический рисунок пути (контура) интегрирования (рис. 2.3).
2) 
Из условия z = 0, следует, что
из условия z = 3+7i, следует, что
3) Установим, как изменяется параметр t при движении от точки z = 0 до точки z = 3 + 7i.
При z = 0 у нас х = 0 и у = 0, а значит, из параметрических уравнений t = 0; при z = 3 + 7i имеем x = 3 и у = 7, тогда из тех же уравнений находим t = 1.
Таким образом, . Используем формулу (2.36):
Если путь интегрирования состоит из двух отрезков, то составляются параметрические уравнения для каждого участка отдельно и находятся два интеграла.
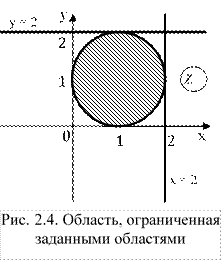
Построить область, заданную на комплексной плоскости
Запишем область в другом виде с учетом, что получим:
Это область, ограниченная окружностью с центром в точке (1, 1) и радиусом 1.
Ограничение запишем в виде:
Ограничение имеет вид:
Получили область, ограниченную графиками:
Изобразим область на графике (рис. 2.4). Заданная область заштрихована.
Найти интеграл от функции комплексного переменного, используя основную теорему Коши:

1) Построим область интегрирования:
Получили уравнение окружности с центром в точке О и радиусом (рис. 2.5).
2) Найдем точки и изобразим их на рисунке 2.5.
Из формулы (2.38) следует, что
Получаем, что . Точка не попадает в область интегрирования, следовательно,
1) Определяем интеграл, используя формулу (2.38):
Найти интеграл от функции комплексного переменного используя основную теорему Коши: .
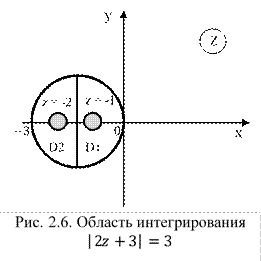
1) Построим область интегрирования:
Получили уравнение окружности с центром в точке О и радиусом (рис. 2.6).
2) Найдем точки и изобразим их на рисунке 2.6.
Из формулы (2.38) следует, что
Обе точки лежат в области интегрирования, следовательно, разбиваем область интегрирования на две замкнутые области D1 и D2. Интеграл разбиваем на два:
3) Определяем интегралы, используя формулу (2.38), найдем интеграл по области D1, где :
Найдем интеграл по области D2, где :
Складываем полученные интегралы и получаем:
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
- Поверхностные интегралы в математике с примерами решения и образцами выполнения
- Поверхностный интеграл первого рода
- Интеграл по цилиндрической поверхности
- Интеграл по сферической поверхности
- Определение и свойства поверхностных интегралов
- Поверхностный интеграл I рода
- Вычисление поверхностного интеграла I рода
- Некоторые приложения поверхностного интеграла I рода
- Площадь поверхности
- Масса поверхности
- Моменты, центр тяжести поверхности
- Поверхностный интеграл II рода
- Вычисление поверхностного интеграла II рода
- Формула Остроградского-Гаусса
- Формула Стокса
- Некоторые приложения поверхностного интеграла II рода
- Калькулятор Интегралов. Решение Определенных и Неопределенных Интегралов (первообразных)
- 💡 Видео
Видео:ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

Поверхностные интегралы в математике с примерами решения и образцами выполнения
При изучении темы «Поверхностные интегралы» вы познакомитесь с понятием интеграла по поверхности от функции трех
переменных и научитесь сводить его к двойному (а затем — к повторному), проецируя заданную поверхность на одну из координатных плоскостей. Кроме того, вы научитесь вычислять интегралы по части цилиндрической и сферической поверхностей.
Видео:Уравнение окружности (1)Скачать

Поверхностный интеграл первого рода
Постановка задачи. Вычислить поверхностный интеграл
где 
и некоторыми неравенствами.
План решения. Поверхностный интеграл сводится к двойному
проецированием 
где D — проекция 
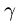
к поверхности 
Замечание:
Если уравнение F(x,y,z) = 0 не определяет однозначно функцию z = z(x,y), то проецируем 
также разбить поверхность на части и воспользоваться аддитивностью интеграла).
1.Единичные нормальные векторы 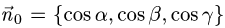
2.Проекцию D поверхности 

3.Находим z = z(x, у), решая уравнение F(x, у, z) = 0.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному.
Пример:
Вычислить поверхностный интеграл
где 
расположенная в первом октанте (т.е. 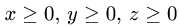
Решение:
1.Единичные нормальные векторы 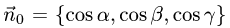
поверхности, заданной уравнением F(x, у, z) = 0, определяются формулой
В данном случае F(x,y,z) = х + 2у + 3z — 1. Следовательно,
2.Поверхность 
Ее проекцию D на плоскость XOY находим, исключая z из условий,
определяющих 
3.Из уравнения х + 2у + 3z — 1 = 0 находим z(x, у) = (1 — х — 2у)/3.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному:
Ответ.
Интеграл по цилиндрической поверхности
Постановка задачи. Вычислить поверхностный интеграл
где 
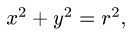
z = 0 и z = h.
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
В этих координатах поверхность задается условиями
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
где 
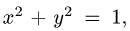
z = 0, z = 2.
Решение:
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
В этих координатах поверхность задается условиями
2.Так как 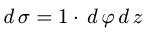
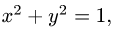
3.Вычисляем повторный интеграл:
Ответ.
Интеграл по сферической поверхности
Постановка задачи. Вычислить поверхностный интеграл
где 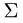
1.Вводим на заданной поверхности (сфере) криволинейные координаты
В этих координатах поверхность задается условиями
2.Так как 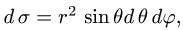
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
где 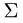
Решение:
1.Вводим на заданной поверхности (сфере) криволинейные координаты
В этих координатах поверхность задается условиями
2.Так как 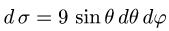
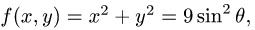
3.Вычисляем повторный интеграл:
Ответ.
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Определение и свойства поверхностных интегралов




Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Поверхностный интеграл I рода
Обобщением двойного интеграла является так называемый поверхностный интеграл.
Пусть в точках некоторой поверхности S, с площадью S , пространства Oxyz определена непрерывная функция f(х; у; z). Разобьем поверхность S на п частей 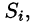
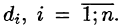
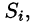
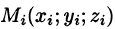
Она называется интегральной для функции f(x;y;z) по поверхности S.
Если при 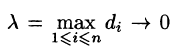
Таким образом, по определению,
Отметим, что «если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f(x;y;z) непрерывна на этой поверхности, то поверхностный интеграл существует» (теорема существования).
Поверхностный интеграл I рода обладает следующими свойствами:
3. Если поверхность S разбить на части 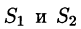
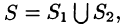
4.Если на поверхности S выполнено неравенство
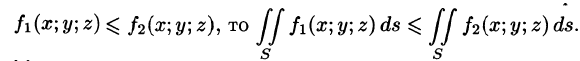
7.Если f(x; у, z) непрерывна на поверхности S, то на этой поверхности существует точка 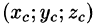
(теорема о среднем значении).
Видео:Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

Вычисление поверхностного интеграла I рода
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области D — проекции поверхности S на плоскость Оху.
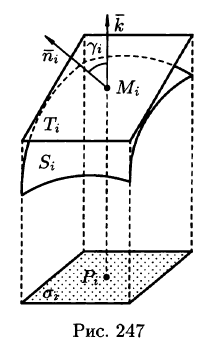
Разобьем поверхность S на части 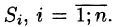
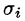
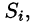
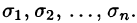
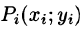
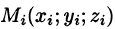
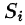
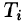
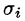
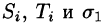
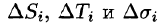

Обозначив через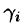
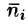
(область 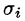
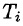
Если поверхность S задана уравнением z = = z(x;y), то, как известно (см. (45.2)), уравнение касательной плоскости в точке 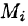
где 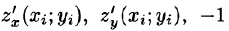
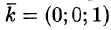
Равенство (57.4) принимает вид
В правой части формулы (57.2) заменим 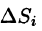
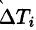
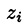
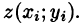
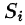
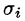
выражающую интеграл по поверхности S через двойной интеграл по проекции S на плоскость Оху.
Отметим, что если поверхность S задана уравнением вида у = y(x;z) или х = x(y;z), то аналогично получим:
где 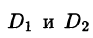
Пример:
Вычислить 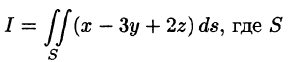
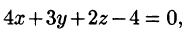
Решение:
Запишем уравнение плоскости в виде
Находим 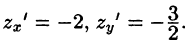
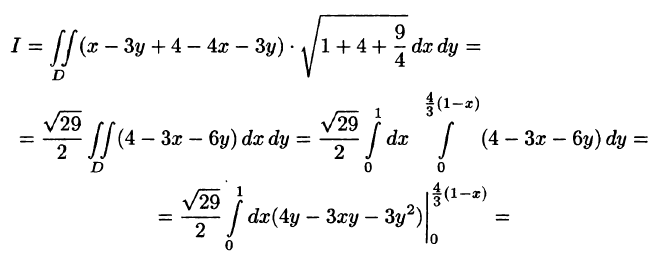
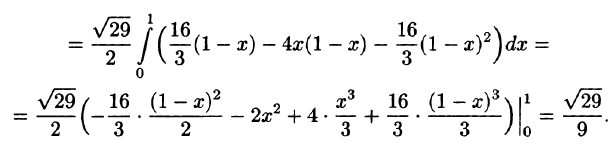
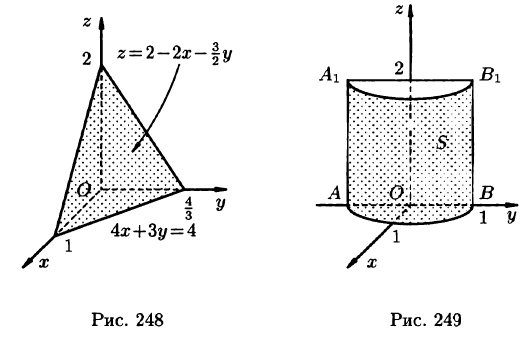
Пример:
где S — часть цилиндрической поверхности 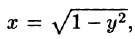
Решение:
Воспользуемся формулой (57.6). Поскольку
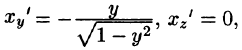
то где 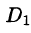
Некоторые приложения поверхностного интеграла I рода
Приведем некоторые примеры применения поверхностного интеграла I рода.
Площадь поверхности
Если поверхность S задана уравнением z = z(x; у), а ее проекция на плоскость Оху есть область D, в которой z(x;y), zx'(x; у) и zy'(x;y) — непрерывные функции, то ее площадь S вычисляется по формуле
Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы 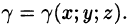
Масса поверхности
Пусть плотность распределения массы материальной поверхности есть 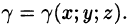
- Разбиваем поверхность S на п частей
площадь которой обозначим
.
- Берем произвольную точку
в каждой области
. Предполагаем, что в пределах области
плотность постоянна и равна значению ее в точке
.
- Масса
области
мало отличается от массы
фиктивной однородной области с постоянной плотностью
4. Суммируя 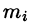
5.За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей 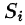
Моменты, центр тяжести поверхности
Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:
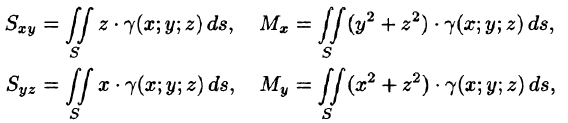
Пример:
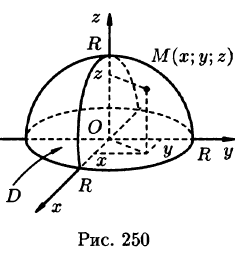
Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы. Решение: На рисунке 250 изображена полусфера радиуса R. Ее уравнение 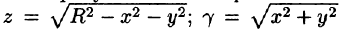
По формуле (57.7) находим:
Переходим к полярным координатам:
внутренний интеграл вычислен с помощью подстановки r= Rsint:
Видео:Уравнение окружностиСкачать

Поверхностный интеграл II рода
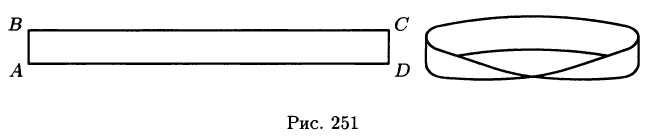
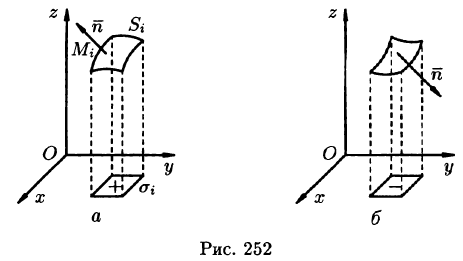
Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.
Пусть задана двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением z =f(x;y), где f(x;y), 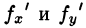
Далее, пусть в точках рассматриваемой двусторонней поверхности S в пространстве Oxyz определена непрерывная функция f(x; у; z). Выбранную сторону поверхности (в таком случае говорят, что поверхность ориентирована) разбиваем на части 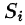
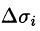
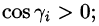
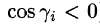
где 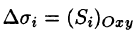
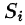
Предел интегральной суммы (58.1) при 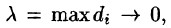
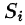
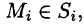
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:
Общим видом поверхностного интеграла II рода служит интеграл
где P, Q, R — непрерывные функции, определенные в точках двусторонней поверхности S.
Отметим, что если S — замкнутая поверхность, то поверхностный интеграл по внешней стороне ее обозначается 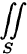
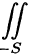
Из определения поверхностного интеграла II рода вытекают следующие его свойства:
- Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
- Постоянный множитель можно выносить за знак поверхностного интеграла.
- Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
- Поверхностный интеграл II рода по всей поверхности
равен сумме интегралов по ее частям
(аддитивное свойство), если
пересекаются лишь по границе, их разделяющей.
- Если
— цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Вычисление поверхностного интеграла II рода
Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла.
Пусть функция R(x; у, z) непрерывна во всех точках поверхности S, заданной уравнением z = z(x; y), где z(x; у) — непрерывная функция в замкнутой области D (или 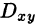
Выберем ту сторону поверхности S, где нормаль к ней образует с осью Oz острый угол. Тогда
Так как 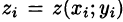
Правая часть этого равенства есть интегральная сумма для функции R(x;y;z(x;y)), непрерывной в области D. Переходя к пределу в равенстве (58.2) при 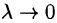
выражающую поверхностный интеграл II рода по переменным х и у через двойной интеграл. Если выбрать вторую сторону, т. е. нижнюю, поверхности S, то полученный двойной интеграл берут со знаком «минус». Поэтому
где 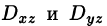
В формуле (58.5) поверхность S задана уравнением у = y(x;z), а в формуле (58.6) — уравнением х = x(y;z). Знаки перед интегралами выбираются в зависимости от ориентации поверхности S (так, в формуле (58.5) берем знак «плюс», если нормаль к поверхности образует с осью Оу острый угол, а знак «минус» — если тупой угол).
Для вычисления общего поверхностного интеграла II рода используют формулы (58.4)-(58.6), проектируя поверхность S на все три координатные плоскости:
Замечание:
Можно показать справедливость равенств
— элемент площади поверхности 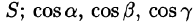
Поверхностные интегралы I и II рода связаны соотношением
Пример:
по верхней стороне части плоскости 2х — Зу + z = 6, лежащей в IV октанте.
Решение:
На рисунке 253 изображена заданная часть плоскости. Нормаль п, соответствующая указанной стороне поверхности, образует с осью Оу тупой угол, а с осями Ох и Oz — острые. В этом можно убедиться, найдя направляющие косинусы нормального вектора 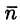
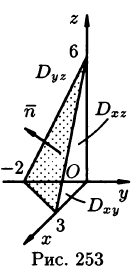
Поэтому перед двойными интегралами в формулах (58.4) и (58.6) следует брать знак «плюс», а в формуле (58.5) — знак «минус». Следовательно,
Формула Остроградского-Гаусса
Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченному этой поверхностью устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y,z), R(x;y;z) непрерывны вместе со своими частными производными первого порядка в пространственной области V, то имеет место формула
где S — граница области V и интегрирование по S производится по ее внешней стороне.
Формула (58.9) называется формулой Остроградского-Гаусса (является аналогом формулы Остроградского-Грина (см. п. 56.3).
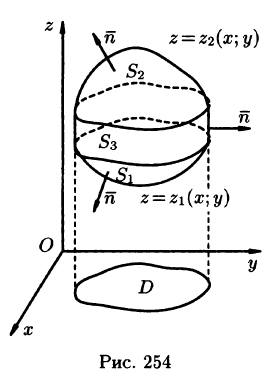
Пусть область V ограничена снизу поверхностью 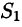
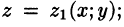
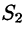
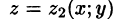
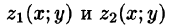
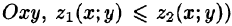
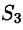
Рассмотрим тройной интеграл
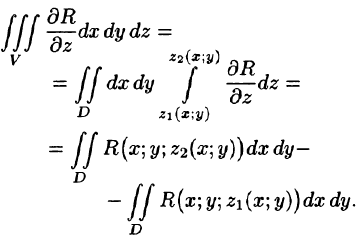
Двойные интегралы в правой части равенства заменим поверхностными интегралами II рода по внешней стороне поверхностей 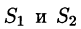
Добавляя равный нулю интеграл 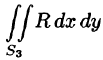
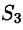
где S — поверхность, ограничивающая область V. Аналогично доказываются формулы
Складывая почленно равенства (58.10), (58.11) и (58.12), получаем формулу (58.9) Остроградского-Гаусса.
Замечания:
- Формула (58.9) остается справедливой для любой области V, которую можно разбить на конечное число областей рассмотренного вида.
- Формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.
Пример:
где S — внешняя сторона пирамиды, ограниченной плоскостями 2х — Зу + z = 6, х = 0, у = 0, z = 0.
Решение:
По формуле (58.9) находим:
Заметим, что интеграл 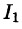
где поверхности 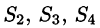
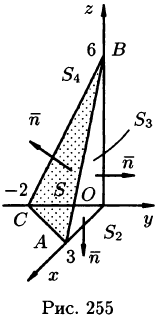
Формула Стокса
Связь между поверхностными и криволинейными интегралами II рода устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y;z) и R(x;y;z) непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности S, то имеет место формула
где L — граница поверхности S и интегрирование вдоль кривой L производится в положительном направлении (т. е. при обходе границы L поверхность S должна оставаться все время слева).
Формула (58.13) называется формулой Стокса (Д. Г. Стоке — английский математик, физик).
Пусть z = f(x;y) — уравнение поверхности S, функции 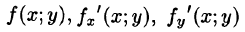
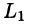
Будем считать, что поверхность S пересекается с любой прямой, параллельной оси Oz, не более чем в одной точке. Выберем верхнюю сторону поверхности S. Рассмотрим сначала интеграл вида
Значения функции Р(х; у; z) на L равны значениям функции P(x; y;z(x;y)) на 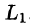
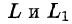
Применим к этому интегралу формулу Остроградского-Грина (см. п. 56.3). Тогда получим:
Преобразуем полученный двойной интеграл в равный ему поверхностный интеграл II рода (см. п. 58.2). Для этого последнее равенство перепишем в виде
(см. 58.7) и используем уравнение нормали к поверхности S (см. (45.3)). Так как выбрана верхняя сторона поверхности S, т. е. 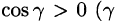
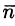
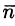
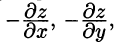
Отсюда 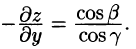
Аналогично получаются при соответствующих условиях еще два равенства:
Складывая почленно три последних равенства, получаем формулу Стокса (58.13).
Отметим, что формулу Стокса (58.13) можно применить и для поверхностей более сложного вида (разбив ее на части рассмотренного выше типа).
Формулу Стокса можно применять для вычисления криволинейного интеграла по замкнутому контуру с помощью поверхностного интеграла.
Из формулы Стокса вытекает, что если выполняются условия
то криволинейный интеграл по произвольному пространственному замкнутому контуру L равен нулю:
Следовательно, в данном случае криволинейный интеграл не зависит от вида пути интегрирования.
Пример:
Вычислить 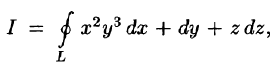
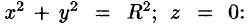
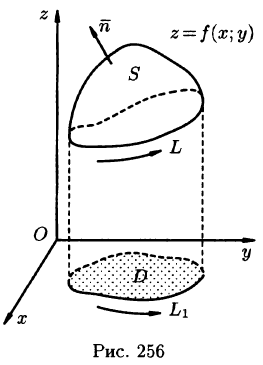
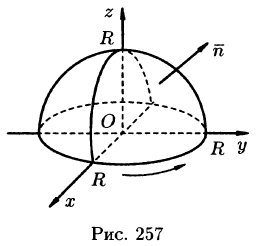
б) используя формулу Стокса, взяв в качестве поверхности полусферу
Решение: Поверхность интегрирования изображена на рисунке 257.
а) Запишем уравнение окружности в параметрической форме:
По формуле (56.7) имеем:
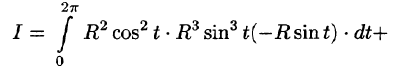
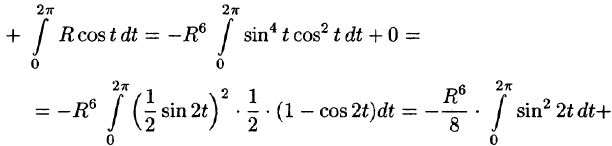
б) По формуле Стокса (58.13) находим:
Переходя к полярным координатам, получаем:
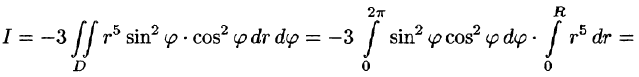
Некоторые приложения поверхностного интеграла II рода
С помощью поверхностного интеграла 11 рода можно найти объем тела, ограниченного сверху поверхностью 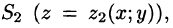
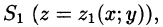
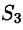
где
Действительно, положив в формуле Остроградского-Гаусса (58.9) 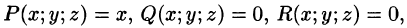
Аналогично, полагая P = 0, Q = у, R = 0, находим еще одну формулу для нахождения объема тела с помощью поверхностного интеграла II рода:
Наконец, положив Р = 0, Q = 0, R = z, по формуле (58.9) находим третью формулу
выражающую объем тела через поверхностный интеграл II рода.
Сложив почленно равенства (58.15)-(58.17) и разделив на три, получим формулу (58.14).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Калькулятор Интегралов. Решение Определенных и Неопределенных Интегралов (первообразных)
| Верхний предел | ∫ |
| Нижний предел | Ввод распознает различные синонимы функций, как asin , arsin , arcsin Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x) Список математических функций и констант : • ln(x) — натуральный логарифм • sh(x) — гиперболический синус • ch(x) — гиперболический косинус • th(x) — гиперболический тангенс • cth(x) — гиперболический котангенс • sch(x) — гиперболический секанс • csch(x) — гиперболический косеканс • arsh(x) — обратный гиперболический синус • arch(x) — обратный гиперболический косинус • arth(x) — обратный гиперболический тангенс • arcth(x) — обратный гиперболический котангенс • arsch(x) — обратный гиперболический секанс • arcsch(x) — обратный гиперболический косеканс 💡 ВидеоСоставляем уравнение окружностиСкачать  УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать  Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать  Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать  Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать  УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать  Площадь фигуры через двойной интеграл в полярных координатахСкачать  Площадь круга через интегралСкачать  УРАВНЕНИЕ ОКРУЖНОСТИ. ЗАДАНИЕ 18 (С5). АРТУР ШАРИФОВСкачать  Уравнение окружности. Практика. Урок 7. Геометрия 9 классСкачать  Как решают уравнения в России и СШАСкачать  |


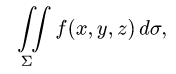
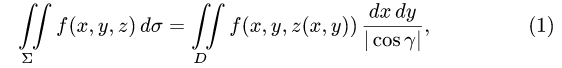
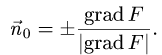
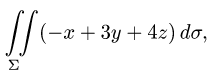
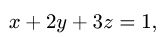
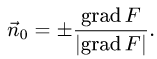
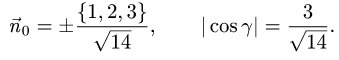
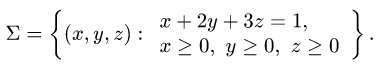
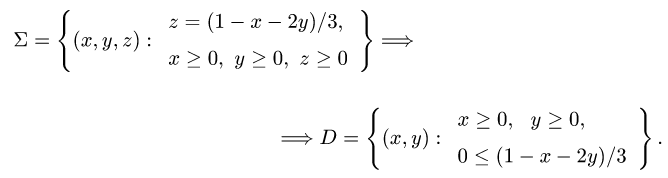
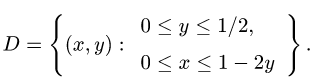
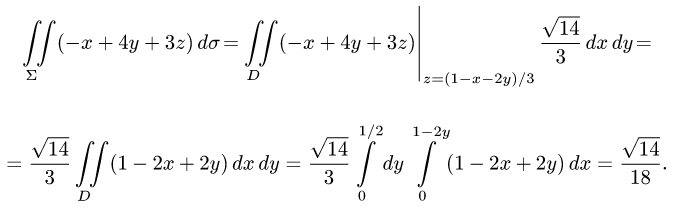
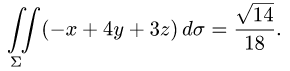
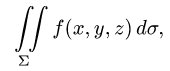
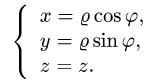
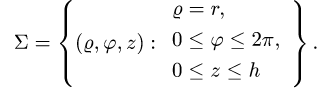
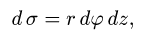
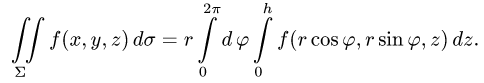
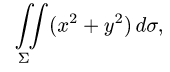
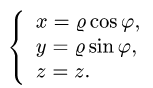
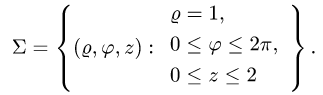
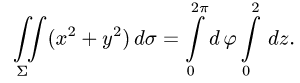
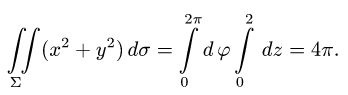
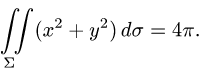
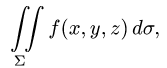
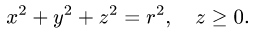
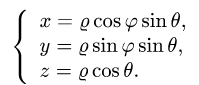
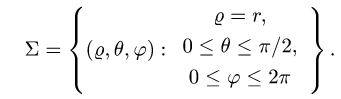
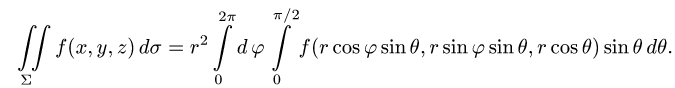
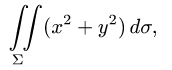
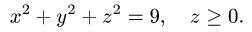
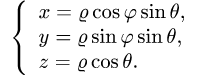
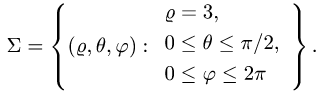
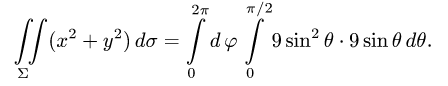
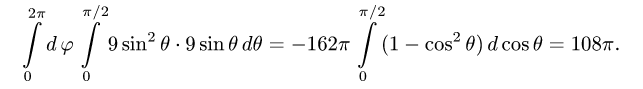
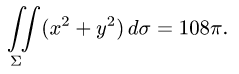


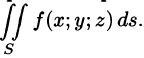
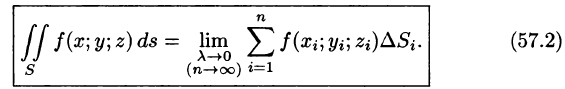
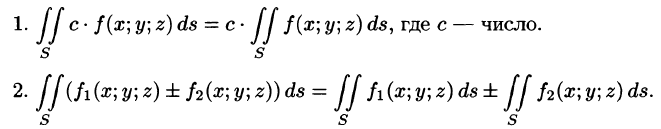
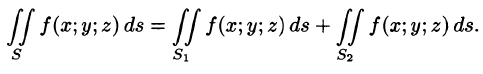
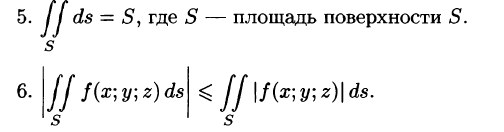
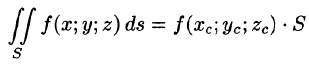
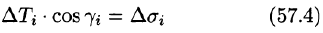
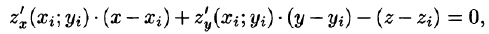
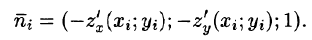
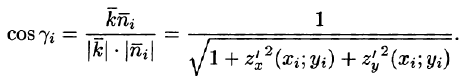
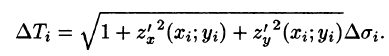
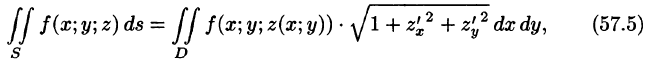
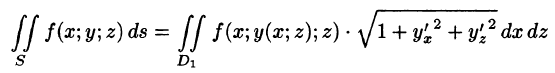
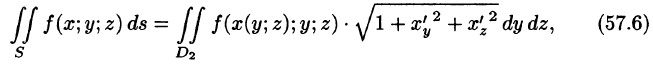
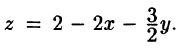
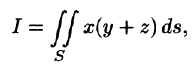
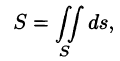
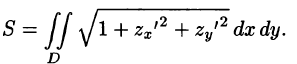
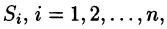 площадь которой обозначим
площадь которой обозначим 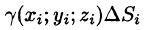 фиктивной однородной области с постоянной плотностью
фиктивной однородной области с постоянной плотностью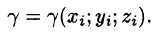
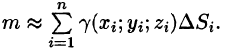
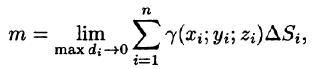
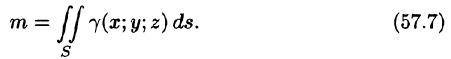
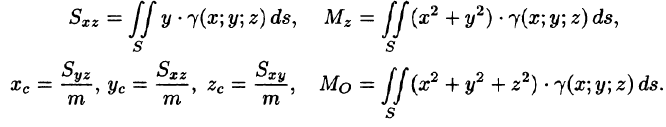
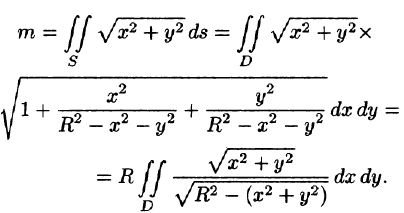
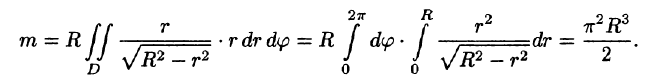
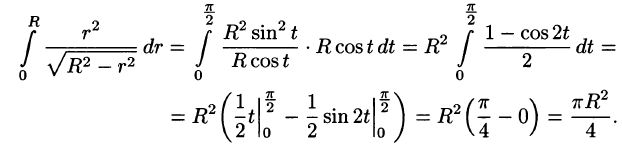

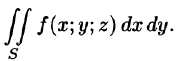
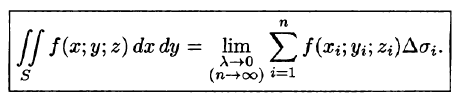
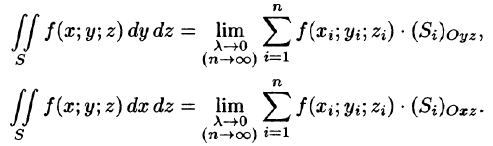
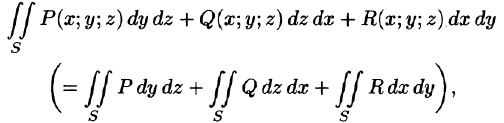
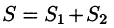 равен сумме интегралов по ее частям
равен сумме интегралов по ее частям 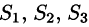 — цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
— цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то