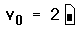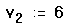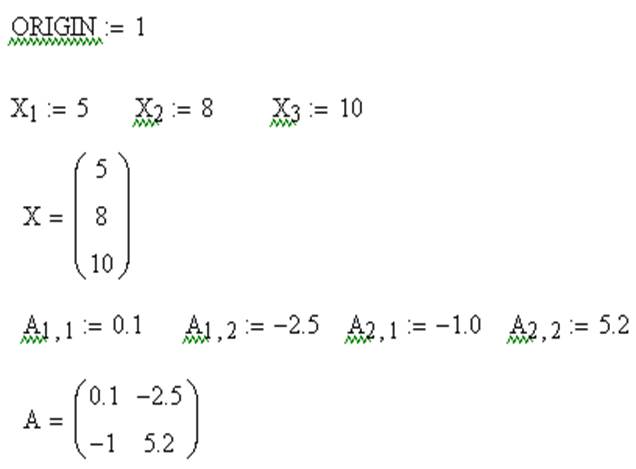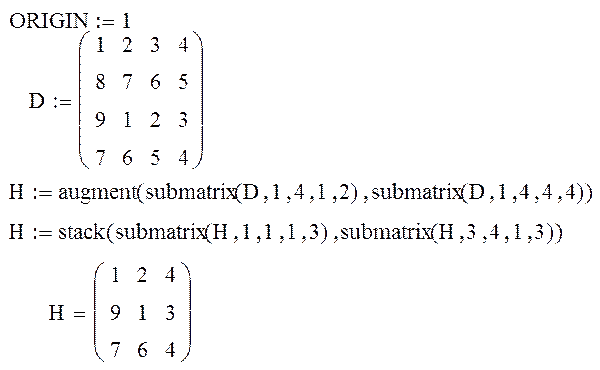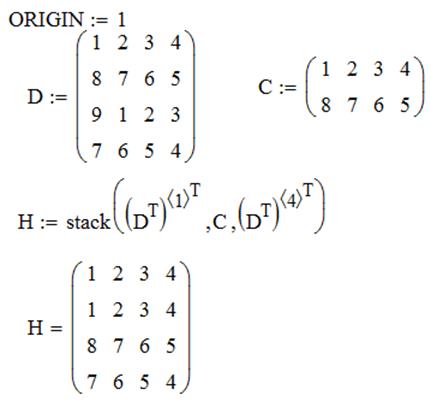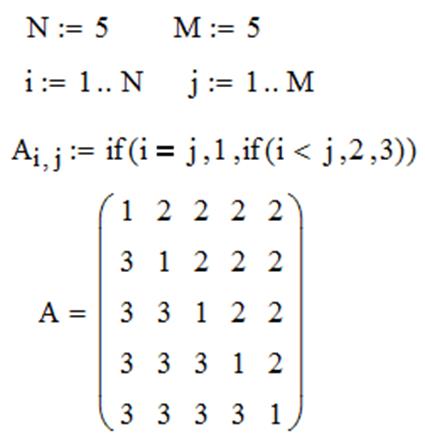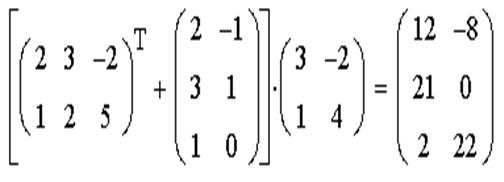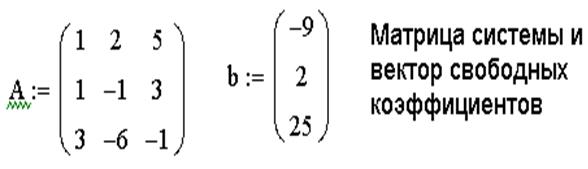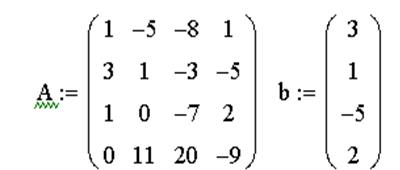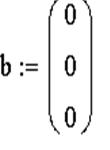Можно обращаться к отдельным элементам массива, используя нижние индексы. Можно также обращаться к отдельному столбцу массива, используя верхний индекс. Чтобы напечатать нижний индекс, используйте клавишу левой скобки [ и поместите в поле целое число или пару целых чисел. Чтобы вставить оператор верхнего индекса, нажмите [Ctrl]6 и поместите в поле целое число.
Вектор и элементы матрицы обычно нумеруются, начиная с нулевой строки и нулевого столбца. Чтобы изменить этот порядок, замените значение встроенной переменной ORIGIN.
Нижние индексы и элементы вектора
Верхнее уравнение на Рисунке 1 определяет вектор v. Чтобы увидеть нулевой элемент вектора v:
- Напечатайте v[0=
Можно также определять отдельные элементы вектора, используя нижний индекс слева от определения. Чтобы заменить значение на 6:
- Напечатайте v[2:6
Рисунок 2 показывает, как это выглядит.
Когда определяются элементы вектора, часть из них можно оставлять неопределенными. Например, если v не был определен, и определяется равным 10, то v0, v1, и v2 все окажутся неопределенными. Mathcad заполняет эти элементы нулями, пока в них не будут внесены необходимые значения. Иллюстрация этого приведена на Рисунке 3. Будьте внимательны: так можно нечаянно создать очень большие векторы и матрицы.
Рисунок 3: Mathcad заполняет нулями все элементы, которые явно не определены.
Нижние индексы и элементы матрицы
Чтобы просматривать или определить элемент матрицы, используйте два нижних индекса, отделяемые запятой. Вообще, чтобы обратиться к элементу в i -той строке и j-том столбце матрицы M, напечатайте:
Обратите внимание, что нижние индексы, подобно делению и возведению в степень удерживают ввод. Что бы ни печаталось после [, всё остается в нижнем индексе, пока не будет нажат [Space], чтобы выйти оттуда.
Если нужно что-то добавить в выражение, нажмите[Space], чтобы заключить все имя элемента матрицы, Mi,j , в выделяющую рамку.
Рисунок 4 показывает некоторые примеры того, как определить отдельные элементы матрицы и как просмотреть их. Обратите внимание, что, как и в случае с векторами, Mathcad заполняет неопределенные элементы матрицы нулями.
Можно также определять элементы вектора или матрицы формулой типа vi :=i, где i — дискретный аргумент. См. следующую главу “Дискретные аргументы”.
Рисунок 4: Определение и просмотр элементов матрицы.
Рисунок 5: Использование оператора верхнего индекса для извлечения столбца из матрицы.
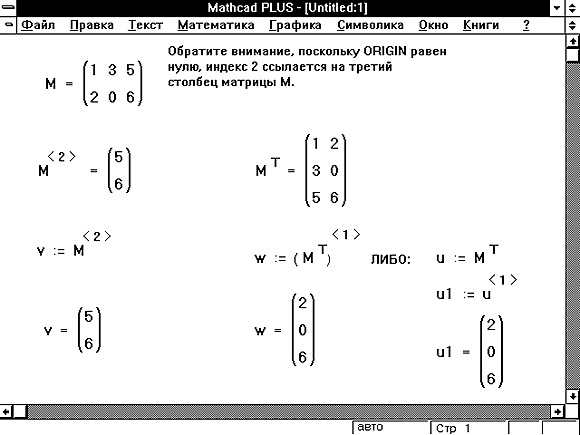
Верхние индексы и столбцы матрицы
Чтобы обратиться ко всему столбцу массива, нажмите [Ctrl]6 и поместите номер столбца в появившееся поле. Рисунок 5 ниже показывает, как присвоить вектору v значение третьего столбца матрицы M.
Можно также извлекать отдельную строку из матрицы, извлекая столбец из транспонированной матрицы. Иллюстрация этого приведена на Рисунке 5.
Изменение значения ORIGIN
По умолчанию массивы Mathcad нумеруются с нулевого элемента. Чтобы изменить этот порядок, замените значение встроенной переменной ORIGIN. Когда используются нижние индексы, Mathcad учитывает, что массивы нумеруются начиная с принятого значения ORIGIN.
Предположим, что нужно, например, чтобы все массивы начинались с первого элемента. Заменить значение ORIGIN во всем документе можно двумя способами:
- Выбрав команду Встроенные переменные из меню Математика и заменив значение ORIGIN.
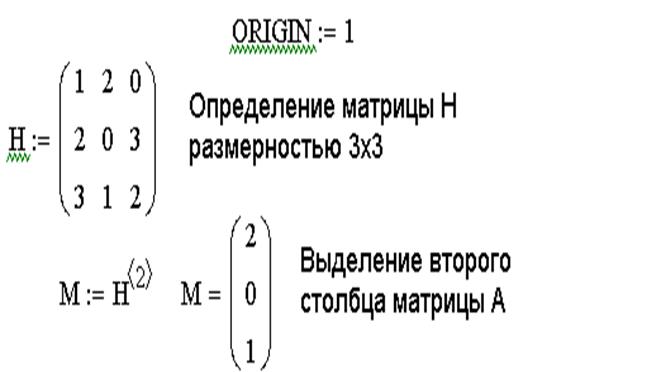
- Введя глобальное определение для ORIGIN в любом месте рабочего документа. Например, чтобы установить значение ORIGIN равное 1, напечатайте: ORIGIN
Рисунок 6: Массивы, нумерующиеся с первого элемента вместо нулевого.
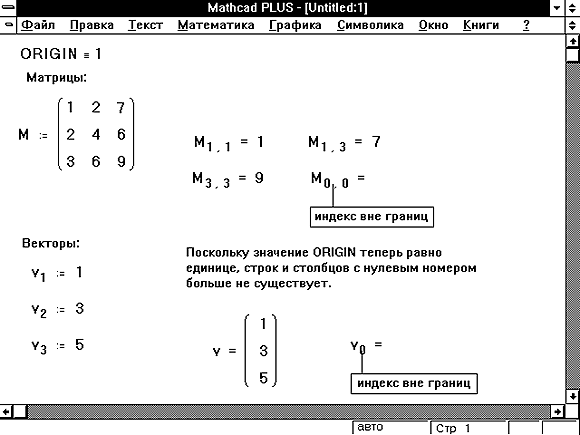
Если изменить ORIGIN на 1, Mathcad больше не будет воспринимать нулевой элемент для векторов или нулевые строки и столбцы для матриц. Рисунок 6 показывает рабочий документ с ORIGIN, равным 1. Заметьте, что при попытке обращения к Mathcad теперь сообщает об ошибке “индекс вне границ”.
При переопределении ORIGIN в рабочем документе имейте в виду следующее:
- Если ORIGIN определяется в рабочем документе, а не с помощью команды Встроенные переменные, используйте одно глобальное определение. Хотя можно переопределять ORIGIN с помощью :=, это приведет к путанице. Если изменить ORIGIN в середине рабочего документа, Mathcad будет показывать, что массивы имеют n элементов, где n — разница между старым и новым значением ORIGIN.
- Не забудьте, что ORIGIN нужно напечатать заглавными буквами. Хотя ORIGIN — встроенная переменная, и она не чувствительна к шрифту, все имена переменных Mathcad, в том числе и встроенных, чувствительны к регистру.
- Когда определяется массив, Mathcad присваивает нулевое значение любым неопределенным элементам. Иллюстрацию этого см. на Рисунке 3 в этой главе.
- Если неосторожно определить массив, начиная с первого элемента, когда ORIGIN установлен на своё значение по умолчанию, равное нулю, будут получаться неожиданные ответы от функций массива подобных mean и fft. Дело в том, что Mathcad будет автоматически определять x0 = 0 для всех этих массивов. Этот дополнительный элемент искажает значения, возвращаемые функциями массива. Чтобы избежать этой проблемы, выберите Встроенные переменные из меню Математика и установите ORIGIN равным 1 в диалоговом окне “Встроенные переменные”.
- Когда ORIGIN устанавливается в диалоговом окне “Встроенные переменные”, его значение применяется ко всем массивам. Невозможно сделать так, чтобы одни массивы использовали один ORIGIN, а другие — другой.
- Можно использовать ORIGIN, чтобы определить переменные с отрицательными нижними индексами. Если ORIGIN устанавливается равным -10, все массивы будут нумероваться с -10.
- Если сослаться на элемент массива с нижним индексом меньшим, чем ORIGIN, Mathcad отмечает обращение к массиву сообщением об ошибке “индекс вне границ”.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Видео:7. MathCad. Векторы и матрицыСкачать

Индекс вектора в маткаде
Глава 3. Работа с векторами и матрицами
3.2 Нумерация элементов и определение параметров матрицы
Нумерация элементов матрицы
Элементы матрицы определяются двумя нижними индексами, элементы вектора – одним.
Для ввода нижнего индекса можно щелкнуть в математической панели на кнопке х n Subscript (Нижний индекс), но лучше использовать клавишу [ (открывающаяся квадратная скобка), так как во время работы с матрицами вводить нижний индекс приходится очень часто.
Чтобы из матрицы выделить вектор (один из столбцов матрицы), используется верхний индекс. Эта операция применяется не очень часто, поэтому для ее выполнения лучше использовать математическую панель инструментов:
– Введите имя матрицы и выделите его синим уголком курсора.
– В математическом меню щелкните на кнопке Matrix and Vector Toolbar (Панель векторов и матриц) и щелкните на кнопке M Matrix Column (Столбец матрицы).
– В появившемся месте ввода пишите номер столбца.
Встроенная переменная ORIGIN
Начало нумерации элементов в векторах и матрицах определяется встроенной переменной ORIGIN .
По умолчанию ORIGIN =0, то есть первый элемент вектора, первая строка и первый столбец матрицы имеют индекс ноль.
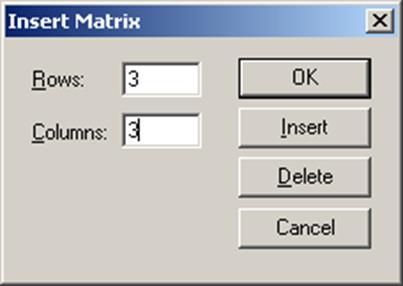
Чтобы изменить нумерацию индексов в первой строке документа, наберите (прописными буквами) ORIGIN :=1. Можно переопределить встроенную переменную ORIGIN другим способом. Выберите в главном меню команду Tools → Worksheet Options (Инструменты→Параметры документа), в открывшемся окне перейдите на вкладку Built – In Variables → ORIGIN (Встроенные переменные) и в поле Array Origin ( ORIGIN ) введите индекс первого элемента массива (рис.4.2). Переменной ORIGIN можно присваивать разные значения, в том числе отрицательные.
В MathCAD есть встроенные функции, в алгоритм которых по умолчанию включены величины с нулевым индексом, например, mean (вычисление среднего значения) или fft (разложение в ряд Фурье). Если ORIGIN :=1 введено с клавиатуры, неизбежна ошибка в расчетах. Измените значения встроенной переменной ORIGIN в главном меню MathCAD , и ошибки в расчетах не будет.


Определение параметров матрицы
В MathCAD есть встроенные функции для определения параметров матрицы (рис. 3.4 ):
– rows ( M ) – число строк в массиве или векторе;
– cols ( M ) – число строк в массиве;
– last ( M ) – индекс последнего элемента в векторе;
– max ( M ) и min ( M ) – максимальное и минимальное значения элементов в массиве
– сумма элементов вектора вычисляется нажатием кнопки ∑ V на панели Matrix ;
– tr ( M ) – сумма диагональных элементов квадратной матрицы, называемая следом матрицы, где M – имя матрицы.


число строк в массиве 
число столбцов в массиве 
индекс последнего элемента в векторе
max и min элементы в массиве


Рис. 3. 4 Функции определения параметров массивов
Видео:Как поставить нижний(верхний) индекс в программе Mathcad (Маткад)Скачать

Векторы и матрицы в MathCAD
Нижняя граница индексации в MathCAD определена системной переменной ORIGIN. По умолчанию ORIGIN=0. Значение переменной можно переопределить. Например, ORIGIN=1.
Векторы и матрицы в MathCAD можно задавать путем ввода их элементов. Для ввода индекса элемента массива используется символ – [.
Поэлементный ввод массива Х
| Вводимые символы | Отображаемые символы |
| X [ 1 Shift+: 5 | X1:=5 |
| X [ 2 Shift+: 8 | X2:= 8 |
| X [ 3 Shift+: 10 | X3:= 10 |
Поэлементный ввод матрицы А
| Вводимые символы | Отображаемые символы |
| A [ 1,1 Shift+: 0.1 | A11 := 0.1 |
| A [ 1,2 Shift+: -2.5 | A12 := -2.5 |
| A [ 2,1 Shift+: -1.0 | A21 := -1.0 |
| A [ 2,2 Shift+: 5.2 | A22 := 5.2 |
Для операций с матрицами и векторами предназначена панель Matrix, которая открывается щелчком по кнопке 
ПанельMatrix содержит следующие кнопки:

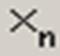
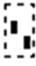

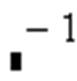

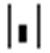
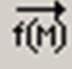
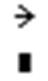
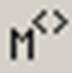
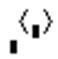






Действия, которые необходимо выполнить, чтобы ввести матрицу в рабочий документ при помощи кнопки 
1. Ввести с клавиатуры имя матрицы и знак присваивания;
2. Щелчком по кнопке 
3. Определить число строк (Rows) и число столбцов (Columns) будущей матрицы;
4. Закрыть окно диалога, щелкнув по кнопке OK;
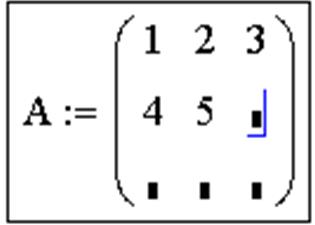
5. Ввести элементы матрицы, установив курсор в поле ввода, которое появится справа от знака присваивания:
Функции определения матриц и операции с блоками матриц:
matrix(m,n,f) – создает и заполняет матрицу A=<aij> размерности m на n, каждый элемент которой aij равен значению функции f(i,j);
diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;
identity(n) – создает единичную матрицу порядка n;
augment(A,B) – из матриц А и В формируется третья матрица, первые столбцыкоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число строк);
stack(A,B) – из матриц А и В формируется третья матрица, первые строкикоторой содержат матрицу А, а последние — матрицу В (матрицы А и В должны иметь одинаковое число столбцов);
submatrix(A,l,k,p,r) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l
Re(A) – возвращает матрицу (вектор) действительных частей матрицы (вектора) А с комплексными элементами;
Im(A) – возвращает матрицу (вектор) мнимых частей матрицы (вектора) А с комплексными элементами;
Функции вычисления различных числовых характеристик матриц:
last(v) – вычисление номера последнего элемента вектора v;
length(v) – вычисление количества элементов вектора v;
rows(A) – вычисление числа строк в матрице А;
cols(A) – вычисление числа столбцов в матрице А;
max(A) – вычисление наибольшего элемента в матрице (векторе) А;
min(A) – вычисление наименьшего элемента в матрице (векторе) А;
mean(A) – вычисление среднего значения матрицы (вектора) А;
tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;
ranc(A) – вычисление ранга матрицы А;
Функции, реализующие численные алгоритмы:
rref(A) – приведение матрицы А к ступенчатому виду;
geninv(A) – вычисляет матрицу, левую обратную к матрице А, L∙A=E, где Е – единичная матрица размером n×n, L – прямоугольная матрица размером n×m, А – прямоугольная матрица размером m×n;
lsolve(A,b) – решение системы линейных алгебраических уравнений A∙x=b.
lu(A) – выполняет треугольное разложение матрицы А: A=С∙L∙U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка;
qr(A) – выполняет разложение матрицы А: A=Q∙R, где Q – ортогональная матрица, а R – верхняя треугольная матрицы;
cholesky(A) – выполняет разложение матрицы А по схеме Холецкого: А=L∙L T , где А — квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;
sort(v) – сортировка элементов вектора v в порядке возрастания их значений;
reverse(v) – перестановка элементов вектора v в обратном порядке;
csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n-й столбец;
rsort(A,n) – перестановка столбцов матрицы А таким образом, чтобы отсортированной оказалась n-я строка.
ЗАДАЧА 1. Сформировать матрицу H из элементов матрицы D, исключив третий столбец и вторую строку.
ЗАДАЧА 2. Сформировать матрицу H следующим образом. Первая и последняя строки равны строкам матрицы D, остальные совпадают с матрицей C.
ЗАДАЧА 3. Сформировать матрицу таким образом, чтобы элементы на главной диагонали были равны 1, выше главной диагонали – 2, а ниже – 3.
ЗАДАЧА 4. Элементы матрицы формируются по формуле 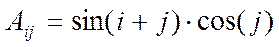
ЗАДАЧА 5. Выполнить действия над матрицами А, В, С:
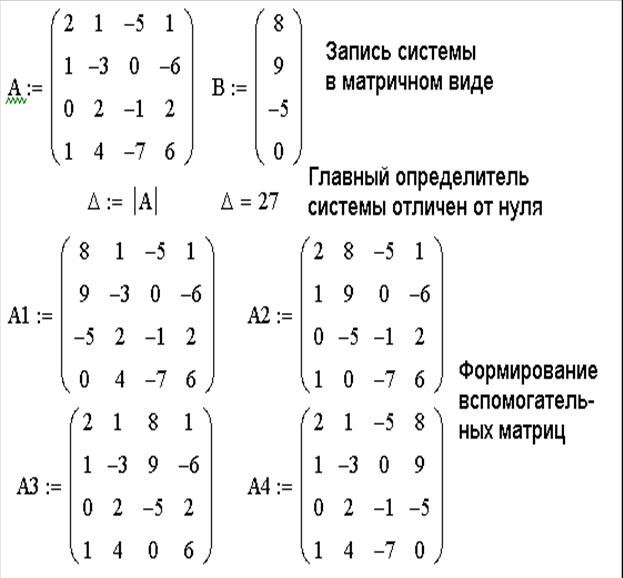
ЗАДАЧА 6. Решить систему линейных уравнений при помощи правила Крамера:
Для решения поставленной задачи необходимо выполнить следующие действия:
1. Сформировать матрицу системы А и вектор правых частей b.
2. Вычислить главный определитель ∆.
3. Сформировать вспомогательные матрицы (удобно скопировать матрицу А несколько раз и последовательно заменять в ней столбцы на вектор b) для вычисления определителей ∆i;
4. Вычислить определители ∆i;
5. Найти решение системы по формуле xi=∆i/∆.
ЗАДАЧА 7. Решить систему линейных уравнений методом обратной матрицы.
1. Сформировать матрицу коэффициентов и вектор свободных членов системы.
2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов.
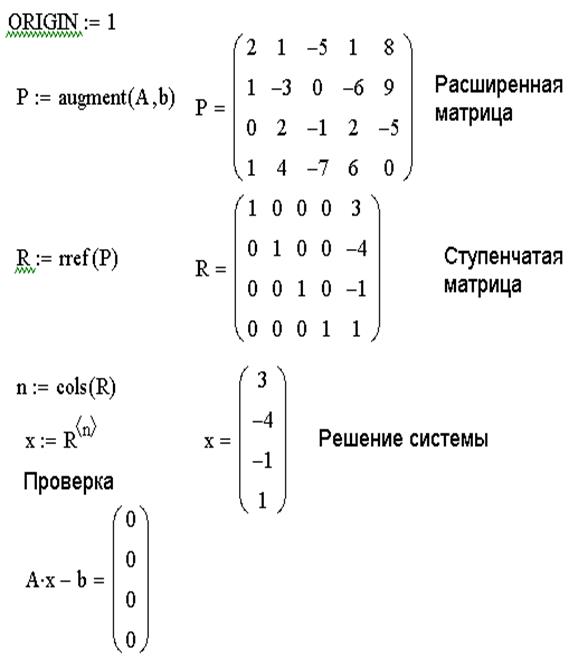
ЗАДАЧА 8. Решить систему линейных уравнений методом Гаусса.
Порядок решения задачи:
1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.
2. Сформировать расширенную матрицу системы при помощи функции augment(A,b);
3. Используя функцию rref(A), привести расширенную матрицу к ступенчатому виду.
4. Получить решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте.
5. Выполнить проверку Ax-B=0.
ЗАДАЧА 9. Решить систему при помощи функции lsolve:
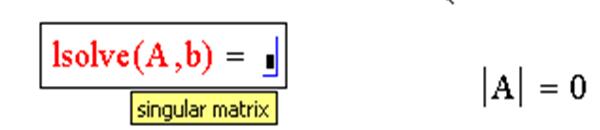
Пример системы, которая не имеет решений:
Пример системы, которая имеет бесконечное множество решений
ЗАДАЧА 10. Решить систему при помощи решающего блока.
Решающий блок начинается с ключевого слова Given (Дано), которое необходимо ввести с клавиатуры.
Правее и ниже ключевого слова записываются уравнения системы.
Знак равенства в уравнениях вводится при помощи клавиш Ctrl+= или выбирается на панели инструментов Boolean.
Правее и ниже последнего уравнения системы вводится функция Find(x1,x2,…xn) (Найти), в скобках перечисляются имена переменных, значения которых нужно найти.
Численное решение системы можно получить, поставив знак равенства после функции Find(x1,x2,…xn).
Символьное решение получится, если после функции Find(x1,x2,…xn) указать знак стрелки, который находится в панели инструментов Symbolic (Ctrl+.).
📽️ Видео
Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать

Векторы и матрицыСкачать
Численные и текстовые индексы в MathCADСкачать

Матрицы в Mathcad(создание и редактирование матриц)(Урок 3.1)Скачать
Функции для работы с матрицами и векторами в MathCAD 14 (21/34)Скачать
Программа MathCAD. Урок 8. Текстовые и численные индексы в MathCADСкачать
Векторная диаграмма токов в программе MathcadСкачать

Основы работы в Mathcad ГрафикиСкачать

Reverse engineering | Исходный код из исполняемого файла | ghidraСкачать

#7. Реализация динамического массива на С++ с помощью std::vector | Структуры данныхСкачать

MathCad компланарность векторов.wmvСкачать

Урок 4. МКЭ в Mathcad. Вектор узловой нагрузкиСкачать

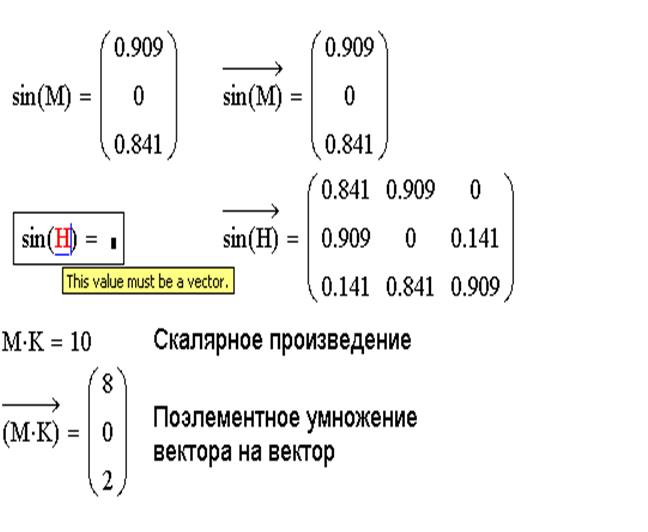
Матрицы. Скалярное и векторное произведение векторов в Mathcad, матричные функции(Урок 3.3)Скачать
Создание матриц в MathCAD 14 (18/34)Скачать
Матрицы и векторы. Настройки Mathcad при работе с матрицами. Урок 12Скачать

PTC Mathcad - Basic Arrays and Range VariablesСкачать

ВекторыСкачать