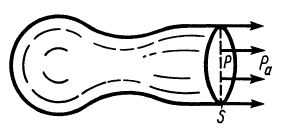
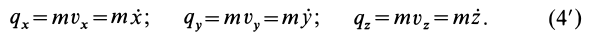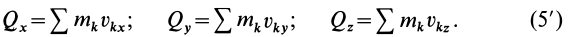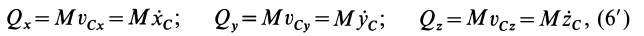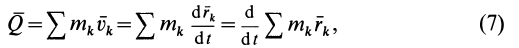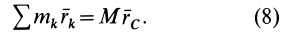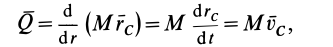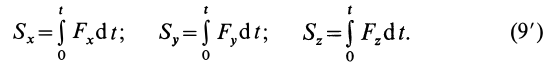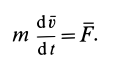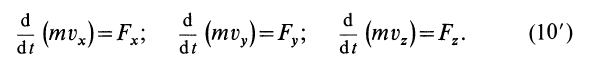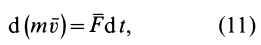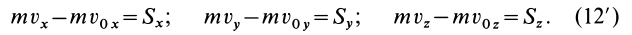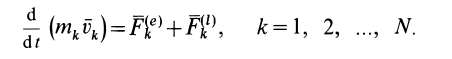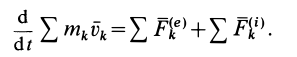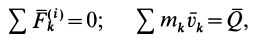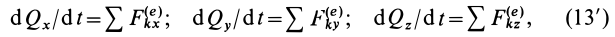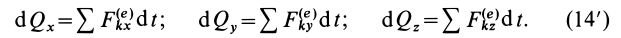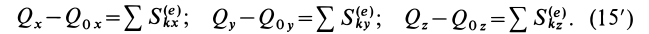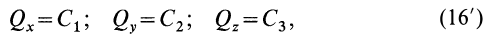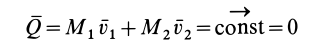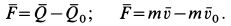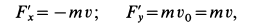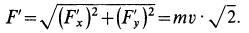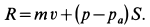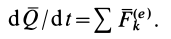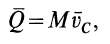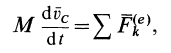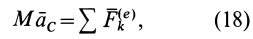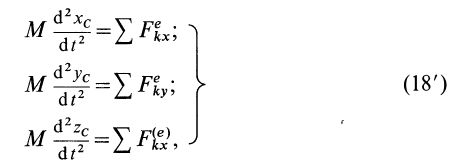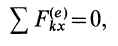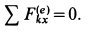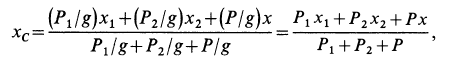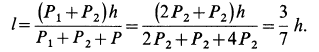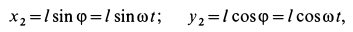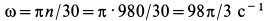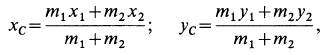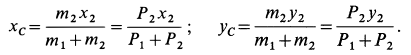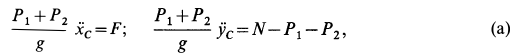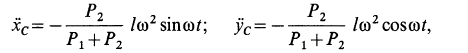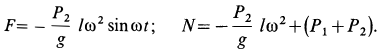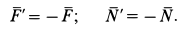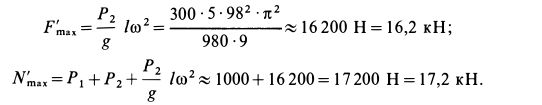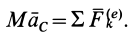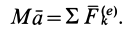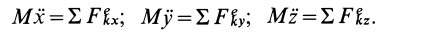§1. Количество движения системы (импульс системы)
Количество движения (импульс тела) – векторная физическая величина, равная произведению массы тела на его скорость:
Импульс (количество движения) – одна из самых фундаментальных характеристик движения тела или системы тел.
Запишем II закон Ньютона в другой форме, учитывая, что ускорение Тогда следовательно
Произведение силы на время ее действия равно приращению импульса тела:
Где — импульс силы, который показывает, что результат действия силы зависит не только от ее значения, но и от продолжительности ее действия.
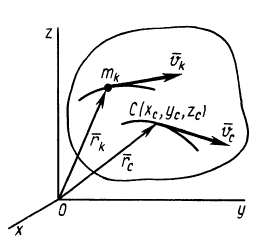
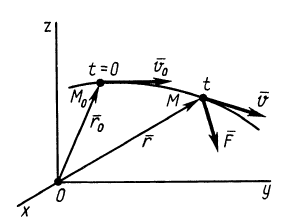
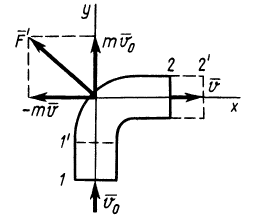
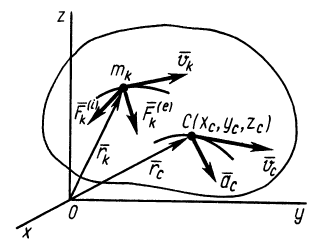
Количеством движения системы (импульсом) будем называть векторную величину , равную геометрической сумме (главному вектору) количеств движения (импульсов) всех точек системы (рис.2):
Из чертежа видно, что независимо от величин скоростей точек системы (если только эти скорости не параллельны) вектор может принимать любые значения и даже оказаться равным нулю, когда многоугольник, построенный из векторов
, замкнется. Следовательно, по величине нельзя полностью судить о характере движения системы.
Рис.2. Количество движения системы
§2. Теорема об изменении количества движения (импульса)
Пусть на тело массой m в течение некоторого малого промежутка времени Δt действовала сила Под действием этой силы скорость тела изменилась на Следовательно, в течение времени Δt тело двигалось с ускорением:
Из основного закона динамики (второго закона Ньютона) следует:
Следовательно, алгебраическое приращение количества движения материальной точки при прямолинейном движении за время ∆t равна импульсу действующей силы за тот же промежуток времени.
§3. Закон сохранения количества движения (закон сохранения импульса)
Из теоремы об изменении количества движения системы можно получить следующие важные следствия:
1) Пусть сумма всех внешних сил, действующих на замкнутую систему, равна нулю:
Тогда из уравнения следует, что Q==const. Таким образом, если сумма всех внешних сил, действующих на замкнутую систему, равна нулю, то вектор количества движения (импульса) системы будет постоянен по модулю и направлению.
2) Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например Оx) равна нулю:
Тогда из уравнения следует, что при этом Qx=const. Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения (импульса) системы на эту ось есть величина постоянная.
Эти результаты и выражают закон сохранения количества движения системы: при любом характере взаимодействия тел, образующих замкнутую систему, вектор полного импульса этой системы все время остается постоянным.
Из них следует, что внутренние силы изменить суммарное количество движения системы не могут.
Закон сохранения полного импульса изолированной системы – это универсальный закон природы. В более общем случае, когда система незамкнута, из следует, что полный импульс незамкнутой системы не остается постоянным. Его изменение за единицу времени равно геометрической сумме всех внешних сил.
Рассмотрим некоторые примеры:
а) Явление отдачи или отката. Если рассматривать винтовку и пулю как одну систему, то давление пороховых газов при выстреле будет силой внутренней. Эта сила не может изменить суммарное количество движения системы. Но так как пороховые газы, действуя на пулю, сообщают ей некоторое количество движения, направленное вперед, то они одновременно должны сообщить винтовке такое же количество движения в обратном направлении. Это вызовет движение винтовки назад, т.е. так называемую отдачу. Аналогичное явление получается при стрельбе из орудия (откат).
б) Работа гребного винта (пропеллера). Винт сообщает некоторой массе воздуха (или воды) движение вдоль оси винта, отбрасывая эту массу назад. Если рассматривать отбрасываемую массу и самолет (или судно) как одну систему, то силы взаимодействия винта и среды как внутренние не могут изменить суммарное количество движения этой системы. Поэтому при отбрасывании массы воздуха (воды) назад самолет (или судно) получает соответствующую скорость движения вперед, такую, что общее количество движения рассматриваемой системы останется равным нулю, так как оно было нулем до начала движения.
Аналогичный эффект достигается действием весел или гребных колес.
в) Реактивное движение. В реактивном снаряде (ракете) газообразные продукты горения топлива с большой скоростью выбрасываются из отверстия в хвостовой части ракеты (из сопла реактивного двигателя). Действующие при этом силы давления будут силами внутренними, и они не могут изменить суммарное количество движения системы ракета — продукты горения топлива. Но так как вырывающиеся газы имеют известное количество движения, направленное назад, то ракета получает при этом соответствующую скорость движения вперед.
Вопросы для самопроверки:
— Что называется количеством движения механической системы?
— Как формулируется теорема об изменении количества движения системы?
— Запишите математическое выражение теоремы об изменении количества движения механической системы в дифференциальной и интегральной форме.
— В каком случае количество движения механической системы не изменяется?
— Как определяется импульс переменной силы за конечный промежуток времени? Что характеризует импульс силы?
— Чему равны проекции импульса постоянной и переменной силы на оси координат?
— Чему равен импульс равнодействующей?
— Как изменяется количество движения точки, движущейся равномерно по окружности?
— Что называется количеством движения механической системы?
— Чему равно количество движения маховика, вращающегося вокруг неподвижной оси, проходящей через его центр тяжести?
— При каких условиях количество движения механической системы не изменяется? При каких условиях не изменяется его проекция на некоторую ось?
— Почему происходит откат орудия при выстреле?
— Могут ли внутренние силы изменить количество движения системы или количество движения ее части?
— От каких факторов зависит скорость свободного движения ракеты?
— Зависит ли конечная скорость ракеты от времени сгорания топлива?
- Теоремы об изменении количества движения и о движении центра масс в теоретической механике
- Вычисление количества движения системы
- Элементарный и полный импульсы силы
- Теорема об изменении количества движения точки
- Теорема об изменении количества движения системы
- Законы сохранения количества движения
- Теорема о движении центра масс системы
- Дифференциальные уравнения поступательного движения твердого тела
- Теоремы об изменении количества движения точки и системы
- Упражнения для самостоятельной работы
- 🎦 Видео
Видео:27. Теорема об изменении главного вектора количества движения механической системыСкачать

Теоремы об изменении количества движения и о движении центра масс в теоретической механике
Содержание:
Количество движения точки и системы:
Одной из мер движения точки или системы является количество их движения.
Количеством движения материальной точки
Количество движения точки в физике часто называют импульсом материальной точки.
Проекции количества движения точки на прямоугольные декартовы оси координат:
Размерность количества движений в СИ — 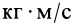
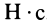
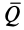
и, следовательно, проекции количества движения системы на прямоугольные декартовы оси координат
Вектор количества движения системы 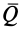
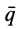
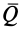
Видео:Количество движения системы ЗадачиСкачать

Вычисление количества движения системы
Количество движения системы можно выразить через массу системы 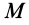
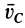
В проекциях на прямоугольные декартовы оси соответственно
где 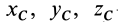
где 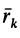
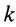
Рис. 40
По формуле для радиуса-вектора центра масс,
Подставляя значение статического момента массы (8) в (7), имеем
так как масса системы 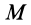
Видео:Момент количества движенияСкачать

Элементарный и полный импульсы силы
Действие силы 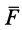
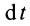
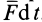
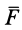
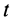
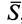
Проекции импульса силы на прямоугольные оси координат выражаются формулами
Единица импульса силы — 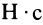
Видео:Меры движения точки и системыСкачать

Теорема об изменении количества движения точки
Дифференциальное уравнение движения материальной точки под действием силы 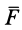
Так как масса точки 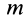
Формула (10) выражает теорему об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе.
В проекциях на координатные оси (10) можно представить в виде
Рис. 41
Если обе части (10) умножить на 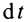
т. е. дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.
Проецируя обе части (11) на координатные оси, получаем
Интегрируя обе части (11) в пределах от нуля до 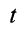
где 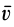
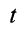
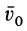
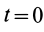
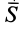
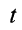
Выражение в форме (12) часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени. В проекциях на координатные оси эту теорему можно представить в следующем виде:
Для материальной точки теорема об изменении количества движения в любой из форм, по существу, не отличается от дифференциальных уравнений движения точки.
Видео:Момент количества движения системыСкачать

Теорема об изменении количества движения системы
Аналогично тому, как для одной материальной точки, выведем теорему об изменении количества движения для системы в различных формах. Пусть к точкам системы приложены внешняя и внутренняя силы. Тогда для каждой точки можно применить теорему об изменении количества движения, например в форме (10) (см. рис. 40):
Суммируя по всем точкам системы правые и левые части этих соотношений и учитывая, что сумма производных равна производной от суммы, получаем
Так как, по свойству внутренних сил и определению количества движения системы,
то приведенное соотношение можно представить в виде
Выражение (13) является теоремой об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих на систему. В проекциях на прямоугольные декартовы оси координат
т. е. производная по времени от проекции количества движения системы на какую-либо координатную ось равна сумме проекций всех внешних сил системы на ту же ось.
Умножая обе части (13) на 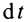
т. е. дифференциал количества движения системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на систему. В проекциях на координатные оси эта теорема примет вид
Вычисляя интегралы от обеих частей (14) по времени- от нуля до получаем теорему импульсов для системы в конечной или интегральной форме:
где 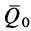
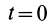
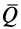
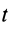
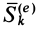
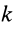
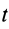
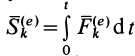
Теорема импульсов для системы в конечной форме формулируется так: изменение количества движения системы за какое-либо время равно векторной сумме всех импульсов внешних сил, действующих на систему за то же время. В проекциях на прямоугольные оси согласно (15) имеем:
Внутренние силы системы не входят явно в теорему об изменении количества движения системы в любой из форм и, следовательно, не влияют непосредственно на изменение количества движения системы. Они могут влиять на изменение количества движения только неявно через внешние силы.
Из теоремы об изменении количества движения для точки и системы при некоторых условиях для внешних сил можно получить так называемые первые интегралы системы дифференциальных уравнений точки и системы. Эти первые интегралы называют законами сохранения количества движения или проекции количества движения на ось. Рассмотрим эти законы сохранения для точки и системы одновременно, считая материальную точку механической системой, состоящей из одной точки.
Законы сохранения количества движения
Законы сохранения количества движения системы получаются как частные случаи теоремы об изменении количества движения для системы в зависимости от особенностей системы внешних сил, приложенных к рассматриваемой механической системе, а для одной точки — от особенностей сил, действующих на точку. Внутренние силы при этом могут быть любыми, так как они явно не влияют на изменение количества движения системы.
Возможны два частных случая.
1. Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, т. е. 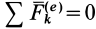
Этот закон (точнее, частный случай теоремы) формулируется так: если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению. В проекциях на координатные оси, по этому закону,
где 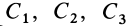
В соотношения (16) и (16′) входят производные от координат точек по времени не выше первого порядка и не входят вторые производные от этих координат. Следовательно, эти соотношения являются первыми интегралами дифференциальных уравнений системы (3).
2. Если равна нулю проекция главного вектора внешних сил на какую-либо координатную ось 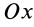
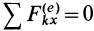
Выражение (17) является законом сохранения проекции количества движения системы: если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю, то проекция количества движения на ту же ось является постоянной величиной.
Применим закон сохранения количества движения системы для объяснения принципа реактивного движения. Пусть, например, система состоит из двух сочлененных твердых тел, находящихся в покое и свободных от действия внешних сил. Тогда для рассматриваемой системы количество движения все время постоянно и равно нулю. Допустим, что при взрыве пиропатрона (действие внутренних сил) первому телу массой 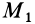
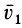
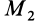
т. е. второе тело движется в сторону, противоположную первому телу. Если его движению препятствует какая-либо связь, то рассматриваемое тело давит на эту связь с некоторой силой по направлению скорости 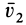
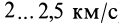
Теорему об изменении количества движения в той или другой форме удобно применять для решения задач именно в рассмотренных частных случаях, хотя в некоторых случаях ее применяют и в общем случае. Отметим, что внутренние силы не влияют на изменение количества движения в изолированных системах, т. е. в системах, которые не соприкасаются с другими телами, не принадлежащими к рассматриваемой системе, или окружающей систему материальной средой.
В неизолированных механических системах внутренние силы, вызывая движение отдельных частей системы вследствие взаимодействия с внешними телами или окружающей материальной средой, могут вызвать внешние силы в виде сил реакций связей или изменения активных сил, которые могут изменить количество движения системы.
Количество движения системы может зависеть от внутренних сил только неявно, через внешние силы.
Рис. 42
Пример №1
Через изогнутую под прямым углом трубу постоянного сечения за 1 с протекает жидкость массой 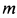
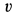
Решение:
Применим к объему жидкости, заключенному между стенками трубы и поперечными сечениями 1 и 2, теорему об изменении количества движения в форме теоремы импульсов за промежуток времени, равный 1 с. За секунду точки жидкости из сечения 1 сместятся на расстояние 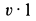
где 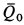
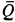
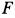
Так как в общей части объема жидкости количества движения, входящие в 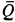
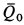
Сила давления жидкости 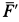
Проецируя (б) на оси координат, получаем
так как 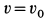
Направление силы давления жидкости 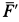
Рис. 43
Если бы через сечение 1 жидкость не поступала, а образовывалась внутри трубы, как в реактивном двигателе образуются газы после сгорания топлива, а через сечение 2 она выходила (рис. 43), то сила 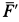
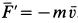
Эта сила 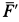
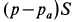
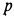
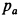
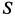
Полная реактивная сила двигателя
По направлению реактивная сила 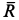
Видео:§4.3. Главный вектор и главный момент сил инерцииСкачать

Теорема о движении центра масс системы
Следствием теоремы об изменении количества движения системы является теорема о движении центра масс системы. По теореме об изменении количества движения системы (13),
Но количество движения системы можно вычислить по формуле (6):
где 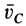
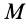
Подставляя (6) в (13) и учитывая, что масса системы постоянна, получаем теорему о движении центра масс в векторной форме:
где 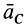
Рис. 44
Теорема о движении центра масс формулируется так: центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к рассматриваемой механической системе.
Проецируя (18) на прямоугольные декартовы оси координат (рис. 44), получаем дифференциальные уравнения движения центра масс:
где 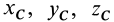
Из теоремы о движении центра масс можно получить следствия, аналогичные законам сохранения количества движения и проекции количества движения на ось.
1. Если главный вектор внешних сил, действующих на систему, равен нулю, т. е. 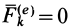
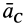
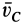
2. Если проекция, например на ось 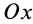
то из (18′) следует, что проекция ускорения 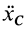
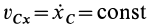
Рис. 45
Если дополнительно в начальный момент 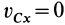
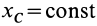
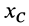
Внутренние силы не влияют явно на движение центра масс. Они могут влиять только неявно, через внешние силы. Следовательно, одними внутренними силами, без внешних, нельзя вывести из равновесия или изменить движение центра масс системы. Но внутренними силами для неизолированной механической системы можно создать движение отдельных частей системы и, следовательно, взаимодействие с внешними телами, вызывая этим внешние силы реакций связей или изменяя активные силы. Это может изменить движение центра масс или вывести его из равновесия.
Пусть человек стоит на абсолютно гладкой горизонтальной плоскости вблизи скрепленного с этой плоскостью тела. Так как на человека не действуют внешние силы в горизонтальном направлении, то внутренними силами он не может вывести из равновесия в этом направлении свой центр масс. Но человек может оттолкнуться рукой от препятствия, т. е. внутренними силами вызвать внешнюю силу реакций препятствия и таким образом вызвать движение своего центра масс в горизонтальном направлении. Все, что движется по Земле, летает в воздухе, плавает по воде, совершает это с помощью внутренних сил, создавая внешние силы трения на твердых поверхностях внешних тел, отталкиваясь от воздуха или воды.
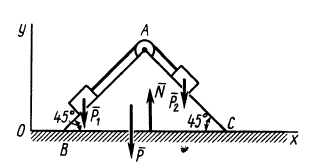
Пример №2
Два груза с силами тяжести 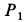
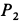
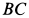
Найти перемещение клина по плоскости при опускании груза 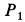
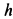
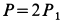
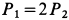
Решение:
Внешними силами, действующими на клин вместе с грузами, являются силы тяжести 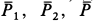
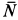
Учитывая, что в начальный момент система находится в покое, на основании второго следствия из теоремы о движении центра масс имеем 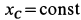
Вычислим 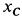
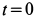
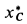
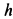
Для момента
где 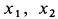
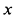
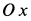
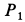
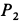
Пусть вся система вместе с клином переместилась в положительном направлении оси 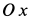
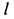
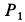
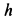
так как грузы вместе с клином передвинутся на 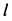
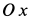
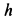
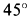
Так как 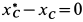
Так как величина 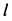
Рис. 46
Пример №3
В электромоторе корпус (статор) имеет силу тяжести 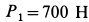
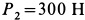
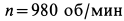
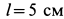
Определить горизонтальную силу, с которой действует мотор на болты, крепящие его к фундаменту, и вертикальное давление на пол.
Решение:
Предположим, что при 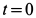
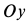
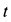
где
Для определения давления мотора на болты и пол рассмотрим в качестве механической системы весь мотор, для которого внешней силой в горизонтальном направлении является только сила действия болтов 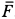
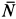
где 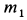
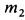
Центр масс корпуса закрепленного мотора является неподвижной точкой и находится в начале координат. Следовательно, 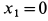
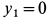
Используя дифференциальные уравнения движения центра масс всего мотора в проекциях на координатные оси, получим
где 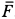
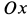
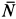
то из (а) следует
Сила действия мотора на болты 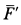
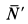
Наибольшие числовые значения этих сил
Если болтов нет, то корпус мотора может подпрыгивать в направлении оси 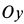
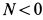
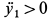
Дифференциальные уравнения поступательного движения твердого тела
Из теоремы о движении центра масс системы получаются дифференциальные уравнения поступательного движения твердого тела. Имеем
Но при поступательном движении твердого тела ускорения всех точек тела одинаковы по модулю и направлению, т. е. 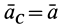
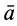
Проецируя на оси координат, имеем:
Это и есть дифференциальные уравнения поступательного движения твердого тела в проекциях на прямоугольные оси координат. В этих уравнениях х, у, z являются координатами произвольной точки тела, в частности могут быть координатами его центра масс. Тело, совершающее поступательное движение, имеет три степени свободы, и поэтому можно составить три дифференциальных уравнения его движения.
Дифференциальные уравнения поступательного движения твердого тела аналогичны дифференциальным уравнениям движения одной материальной точки. С помощью этих уравнений можно решать такие же задачи, как и для одной точки.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Теорема об изменении кинетического момента
- Теорема об изменении кинетической энергии
- Потенциальное силовое поле
- Закон сохранения механической энергии
- Относительное движение материальной точки
- Геометрия масс
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Теорема об изменении количества движенияСкачать

Теоремы об изменении количества движения точки и системы
Количеством движения материальной точки называется векторная величина mV, равная произведению массы точки на вектор ее скорости. Вектор mV приложен к движущейся точке.
Количеством движения системы называют векторную величину Q, равную геометрической сумме (главному вектору) количеств движения всех точек системы:
Вектор Q является свободным вектором. В системе единиц СИ модуль количества движения измеряется в кг • м/с или Н • с.
Как правило, скорости всех точек системы различны (см., например, распределение скоростей точек катящегося колеса, показанное на рис. 6.21), и поэтому непосредственное суммирование векторов в правой части равенства (17.2) является затруднительным. Найдем формулу, с помощью которой величина Q вычисляется значительно легче. Из равенства (16.4) следует, что
Взяв от обеих частей производную по времени, получим 
т. е. количество движения системы равно произведению массы всей системы на скорость ее центра масс.
Заметим, что вектор Q, подобно главному вектору сил в статике, является некоторой обобщенной векторной характеристикой движения всей механической системы. В общем случае движения системы ее количество движения Q можно рассматривать как характеристику поступательной части движения системы вместе с ее центром масс. Если при движении системы (тела) центр масс неподвижен, то количество движения системы будет равно нулю. Таково, например, количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс.
Пример. Определить количество движения механической системы (рис. 17.1, а), состоящей из груза А массой тА — 2 кг, однородного блока В массой 1 кг и колеса D массой mD — 4 кг. Груз А движется со скоростью VA — 2 м/с, колесо D катится без скольжения, нить нерастяжима и невесома. Решение. Количество движения системы тел
Тело А движется поступательно и QA =mAVA (численно QA = 4 кг • м/с, направление вектора QA совпадает с направлением VA). Блок В совершает вращательное движение вокруг неподвижной оси, проходящей через его центр масс; следовательно, QB — 0. Колесо D совершает плоскопараллельное
движение; его мгновенный центр скоростей находится в точке К, поэтому скорость его центра масс (точки Е) равна VE = VA/2= 1 м/с. Количество движения колеса QD — mDVE — 4 кг • м/с; вектор QD направлен горизонтально влево.
Изобразив векторы QA и QD на рис. 17.1, б, находим количество движения Q системы по формуле (а). Учитывая направления и числовые значения величин, получим Q
кг • м/с, направление вектора Q показано на рис. 17.1, б.
Учитывая, что a -dV/dt, уравнение (13.4) основного закона динамики можно представить в виде
Уравнение (17.4) выражает теорему об изменении количества движения точки в дифференциальной форме: в каждый момент времени производная по времени от количества движения точки равна действующей на точку силе. (По существу это другая формулировка основного закона динамики, близкая к той, которую дал Ньютон.) Если на точку действует несколько сил, то в правой части равенства (17.4) будет равнодействующая сил, приложенных к материальной точке.
Если обе части равенства умножить на dt, то получим
Векторная величина, стоящая в правой части этого равенства, характеризует действие, оказываемое на тело силой за элементарный промежуток времени dt эту величину обозначают dS и называют элементарным импульсом силы, т. е.
Импульс S силы F за конечный промежуток времени /, — /0 определяется как предел интегральной суммы соответствующих элементарных импульсов, т. е.
В частном случае, если сила F постоянна по модулю и по направлению, то S = F(t| -/0) и S— F(tl — /0). В общем случае модуль импульса силы может быть вычислен по его проекциям на координатные оси:
Теперь, интегрируя обе части равенства (17.5) при т = const, получим
Уравнение (17.9) выражает теорему об изменении количества движения точки в конечной (интегральной) форме: изменение количества движения точки за некоторый промежуток времени равно импульсу действующей на точку силы (или импульсу равнодействующей всех приложенных к ней сил) за тот же промежуток времени.
При решении задач пользуются уравнениями этой теоремы в проекциях на координатные оси
Теперь рассмотрим механическую систему, состоящую из п материальных точек. Тогда для каждой точки можно применить теорему об изменении количества движения в форме (17.4), учитывая приложенные к точкам внешние и внутренние силы:
Суммируя эти равенства и учитывая, что сумма производных равна производной от суммы, получаем
Так как по свойству внутренних сил HFk =0 и по определению количества движения ^fnkV/c = Q, то окончательно находим
Уравнение (17.11) выражает теорему об изменении количества движения системы в дифференциальной форме: в каждый момент времени производная по времени от количества движения системы равна геометрической сумме всех внешних сил, действующих на систему.
Проецируя равенство (17.11) на координатные оси, получим
Умножая обе части (17.11) на dt и интегрируя, получим
где 0,, Q0 — количества движения системы в моменты времени соответственно и /0.
Уравнение (17.13) выражает теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за какое-либо время равно сумме импульсов всех внешних сил, действующих на систему за то же время.
В проекциях на координатные оси получим
Из теоремы об изменении количества движения системы можно получить следующие важные следствия, которые выражают закон сохранения количества движения системы.
- 1. Если геометрическая ^умма всех внешних сил, действующих на систему, равна нулю (LFk =0), то из уравнения (17.11) следует, что при этом Q = const, т. е. вектор количества движения системы будет постоянен по модулю и направлению.
- 2. Если внешние силы, действующие на систему, таковы, что сумма их проекций на какую-либо ось равна нулю (например, I e kx = 0), то из уравнений (17.12) следует, что при этом Qx = const, т. е. проекция количества движения системы на эту ось остается неизменной.
Отметим, что внутренние силы системы не участвуют в уравнении теоремы об изменении количества движения системы. Эти силы, хотя и влияют на количество движения отдельных точек системы, не могут изменить количество движения системы в целом. Учитывая это обстоятельство, при решении задач рассматриваемую систему целесообразно выбирать так, чтобы неизвестные силы (все или их часть) сделать внутренними.
Закон сохранения количества движения удобно применять в тех случаях, когда по изменению скорости одной части системы надо определить скорость другой ее части.
Задача 17.1. К тележке массой тх — 12 кг, движущейся по гладкой горизонтальной плоскости, в точке А с помощью цилиндрического шарнира прикреплен невесомый стержень AD длиной /= 0,6 м с грузом D массой т2 — 6 кг на конце (рис. 17.2). В момент времени /0 = 0, когда скорость тележки и <)— 0,5 м/с, стержень AD начинает вращаться вокруг оси А, перпендикулярной плоскости чертежа, по закону ф = (тг/6)(3^ 2 — 1) рад (/—в секундах). Определить: u=f[t) — закон изменения скорости тележки.
Решение. Рассмотрим механическую систему, состоящую из тележки и груза D, в произвольном положении (см. рис. 17.2). Отметим, что для удобства дальнейших расчетов в качестве произвольного положения системы изображается такое ее положение, при котором все координаты ее элементов (частей системы) будут положительными.
Изобразим действующи^ на_ систему_ внешние силы: силы тяжести Р|, Р2 и реакции плоскости N’, N» (сила Рх приложена в центре тяжести Сх тележки, который будем считать расположенным под точкой А). Сил трения нет, так как плоскость гладкая. Проведем связанные с неподвижной плоскостью координатные оси Оху так, чтобы ось х была горизонтальна.
Чтобы определить и, воспользуемся теоремой об изменении количества движения системы в проекциях на горизонтальную ось х:
Так как все внешние силы вертикальны, то 2F e kx =0. Следовательно, Qx — const. Обозначив через С значение этой постоянной величины, получим
Для рассматриваемой механической системы Q = Q Т +Q°, где Q т =т^и и Q D =m2VD — количества движения тележки и груза D соответственно (скорость й тележки и скорость VD груза определяются по отношению к неподвижной системе отсчета Оху).
Тогда из равенства (а) следует, что
Для определения VDx рассмотрим движение груза D как сложное, считая его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня ЛД вокруг оси А), а движение самой тележки — переносным. Тогда VD = Ve + Vr и
Но Ve = u и, следовательно, Vex= и. Вектор Vr направлен перпендикулярно стержню AD и численно равен Vr =koAD =Ар = Int. Изобразим этот вектор на рис. 17.2, считая величину ф положительной, и найдем Vtx — — — Vr cos ф. Окончательно равенство (в) примет вид
Подставив это выражение в равенство (б), получим
Отметим, что это равенство справедливо в любой момент времени. Постоянную интегрирования С определим по начальным условиям: при /0 = 0 и — и0. Подстановка этих значений в (д) дает С — (т <+ т2)и0, и тогда уравнение (д) примет вид
Отсюда находим зависимость скорости и тележки от времени
Подставив сюда значения соответствующих величин, находим искомую зависимость u—j <t),м/с.
Ответ: и — [0,5 + 0,2n/cos(rc/ 2 /2 — п/6)].
§ 17.3. Теорема о движении центра масс
Теорему об изменении количества движения механической системы можно выразить еще в другой форме, носящей название теоремы о движении центра масс.
Подставив в уравнение (17.11) равенство Q =MVC, получим
Если масса М системы постоянна, то получим
где ас — ускорение центра масс системы.
Уравнение (17.15) и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех внешних сил, действующих на систему.
Проецируя равенство (17.15) на координатные оси, получим
где xc, yc, zc — координаты центра масс системы.
Эти уравнения представляют собой дифференциальные уравнения движения центра масс в проекциях на оси декартовой системы координат.
Обсудим полученные результаты. Предварительно напомним, что центр масс системы является геометрической точкой, расположенной подчас вне геометрических границ тела. Действующие же на механическую систему силы (внешние и внутренние) приложены ко всем материальным точкам системы. Уравнения (17.15) дают возможность определить движение центра масс системы, не определяя движения отдельных ее точек. Сопоставив уравнения (17.15) теоремы о движении центра масс и уравнения (13.5) второго закона Ньютона для материальной точки, приходим к заключению: центр масс механической системы движется как материальная точка, масса которой равна массе всей системы, и как будто бы к этой точке приложены все внешние силы, действующие на систему. Таким образом, решения, которые получаем, рассматривая данное тело как материальную точку, определяют закон движения центра масс этого тела.
В частности, если тело движется поступательно, то кинематические характеристики всех точек тела и его центра масс одинаковы. Поэтому поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе всего тела.
Как видно из (17.15), внутренние силы, действующие на точки системы, не оказывают влияния на движение центра масс системы. Внутренние силы могут оказать влияние на движение центра масс в тех случаях, когда под их воздействием меняются внешние силы. Примеры этого будут приведены далее.
Из теоремы о движении центра масс можно получить следующие важные следствия, которые выражают закон сохранения движения центра масс системы.
1. Если геометрическая сумма всех внешних сил, действующих на систему, равна нулю (LFk =0), то из уравнения (17.15) следует,
что при этом ас = 0 или Vc = const, т. е. центр масс этой системы
движется с постоянной по модулю и направлению скоростью (иначе, равномерно и прямолинейно). В частном случае, если вначале центр масс был в покое (Vc =0), то он и останется в покое; откуда
след ует, что его положение в пространстве не изменится, т. е. rc = const.
2. Если внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например, ось х) равна нулю (?F e kx = 0), то из уравнения (17.16) следует, что при этом хс =0 или VCx =хс = const, т. е. проекция скорости центра масс системы на эту ось есть величина постоянная. В частном случае, если в начальный момент Vex = 0, то и в любой последующий момент времени это значение сохранится, а отсюда следует, что координата хс центра масс системы не изменится, т. е. хс — const.
Рассмотрим примеры, иллюстрирующие закон движения центра масс.
Примеры. 1. Как было отмечено, движение центра масс зависит только от внешних сил, внутренними силами изменить положение центра масс нельзя. Но внутренние силы системы могут вызвать внешние воздействия. Так, движение человека по горизонтальной поверхности происходит под действием сил трения между подошвами его обуви и поверхностью дороги. Силой своих мышц (внутренние силы) человек ногами отталкивается от поверхности дороги, отчего в точках контакта с дорогой возникает сила трения (внешняя для человека), направленная в сторону его движения.
- 2. Аналогичным образом двигается автомобиль. Внутренние силы давления в его двигателе заставляют вращаться колеса, но так как последние имеют сцепление с дорогой, то возникающие силы трения «толкают» машину вперед (в результате колеса не вращаются, а двигаются плоскопараллельно). Если же дорога будет абсолютно гладкой, то центр масс автомобиля будет неподвижен (при нулевой начальной скорости) и колеса при отсутствии трения будут пробуксовывать, т. е. совершать вращательное движение.
- 3. Движение с помощью гребного винта, пропеллера, весел происходит за счет отбрасывания некоторой массы воздуха (или воды). Если рассматривать отбрасываемую массу и движущееся тело как одну систему, то силы взаимодействия между ними, как внутренние, не могут изменить суммарное количество движения этой системы. Однако каждая из частей этой системы будет двигаться, например, лодка вперед, а вода, которую отбрасывают весла, — назад.
- 4. В безвоздушном пространстве при движении ракеты «отбрасываемую массу» следует «брать с собой»: реактивный двигатель сообщает движение ракете за счет отброса назад продуктов горения топлива, которым заправлена ракета.
- 5. При спуске на парашюте можно управлять движением центра масс системы человек — парашют. Если мышечными усилиями человек подтягивает стропы парашюта так, что меняется форма его купола либо угол атаки воздушного потока, то это вызовет изменение и внешнего воздействия воздушного потока, а тем самым оказывается влияние на движение всей системы.
Задача 17.2. В задаче 17.1 (см. рис. 17.2) определить: 1) закон движения тележки х< = /)(/), если известно, что в начальный момент времени t0 = О система находилась в покое и координата х10 = 0; 2) ^акон изменения со временем суммарного значения нормальной реакции N(N = N’ + N») горизонтальной плоскости, т. е. N=f2(t).
Решение. Здесь, как и в задаче 17.1, рассмотрим систему, состоящую из тележки и груза D, в произвольном положении под действием приложенных к ней внешних сил (см. рис. 17.2). Координатные оси Оху проведем так, чтобы ось х была горизонтальна, а ось у проходила через точку А0, т. е. место расположения точки А в момент времени t—t0 — 0.
1. Определение закона движения тележки. Для определения х, = /,(0 воспользуемся теоремой о движении центра масс системы. Составим дифференциальное уравнение его движения в проекции на ось х:
Так как все внешние силы вертикальны, то T,F e kx = 0, и, следовательно,
Проинтегрировав это уравнение, найдем, что Мхс = В, т. е. проекция скорости центра масс системы на ось х есть величина постоянная. Так как в начальный момент времени
Интегрируя уравнение Мхс = 0, получим
т. е. координата хс центра масс системы постоянна.
Запишем выражение Мхс для произвольного положения системы (см. рис. 17.2), приняв во внимание, что хА — х<, xD — х2 и х2 — х< — I sin ф. В соответствии с формулой (16.5), определяющей координату центра масс системы, в данном случае Мхс — т<х< + т2х2‘.
для произвольного момента времени
В соответствии с равенством (б) координата хс центра масс всей системы остается неизменной, т. е. хД^,) = xc(t). Следовательно, приравняв выражения (в) и (г), получим зависимость координаты х, от времени.
О т в е т: Х — 0,2[0,5 + sin(n/ 2 /2 — 7т/6)] м, где t — в секундах.
2. Определение реакции N. Для определения N=f2(t) составим дифференциальное уравнение движения центра масс системы в проекции на вертикальную ось у (см. рис. 17.2):
Отсюда, обозначив N= N + N», получим
1 cos Ф» получим
Продифференцировав это равенство два раза по времени (учитывая при этом, что уС1 и уА величины постоянные и, следовательно, их производные равны нулю), найдем
Подставив это выражение в уравнение (е), определим искомую зависимость N от t.
где ф = (я/6)(3/ —1), t — в секундах, N— в ньютонах.
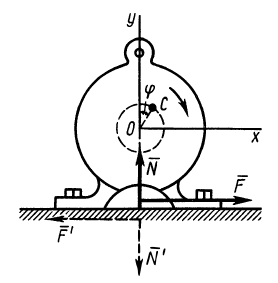
Задача 17.3. Электрический мотор массой тх прикреплен на горизонтальной поверхности фундамента болтами (рис. 17.3). На валу мотора под прямым углом к оси вращения закреплен одним концом невесомый стержень длиной /, на другом конце стержня насажен точечный груз А массой т2. Вал вращается равномерно с угловой скоростью со. Найти горизонтальное давление мотора на болты. Решение. Рассмотрим механическую систему, состоящую из мотора и точечного груза А, в произвольном положении. Изобразим действующие на систему внешние силы: силы тяжести Рх, Р2, реакцию фундамента в виде вертикальной силы N и горизонтальной силы R. Проведем координатную ось х горизонтально.
Чтобы определить горизонтальное давление мотора на болты (а оно будет численно равно реакции R и направлено противоположно вектору R), составим уравнение теоремы об изменении количества движения системы в проекции на горизонтальную ось х:
Для рассматриваемой системы в ее произвольном положении, учитывая, что количество движения корпуса мотора равно нулю, получим Qx = — т2УАсощ. Принимая во внимание, что VA = aз/, ф = со/ (вращение мотора равномерное), получим Qx — — m2co/cos со/. Дифференцируя Qx по времени и подставляя в равенство (а), найдем R— m2co 2 /sin со/.
Заметим, что именно такие силы являются вынуждающими (см. § 14.3), при их воздействии возникают вынужденные колебания конструкций.
Видео:Количество движения системыСкачать

Упражнения для самостоятельной работы
- 1. Что называют количеством движения точки и механической системы?
- 2. Как изменяется количество движения точки, равномерно движущейся по окружности?
- 3. Что характеризует импульс силы?
- 4. Влияют ли внутренние силы системы на ее количество движения? На движение ее центра масс?
- 5. Как влияют на движение центра масс системы приложенные к ней пары сил?
- 6. При каких условиях центр масс системы находится в покое? движется равномерно и прямолинейно?
7. В неподвижной лодке при отсутствии течения воды на корме сидит взрослый человек, а на носу лодки — ребенок. В каком направлении переместится лодка, если они поменяются местами?
В каком случае модуль перемещения лодки будет большим: 1) если ребенок перейдет к взрослому на корму; 2) если взрослый перейдет к ребенку на нос лодки? Каковы будут при этих движениях перемещения центра масс системы «лодка и два человека»?
🎦 Видео
Теоретическая механика. Динамика.Скачать

Теорема об изменении количества движения точкиСкачать

§ 2.2. Количество движения. Импульс силыСкачать

Урок 104. Импульс. Закон сохранения импульсаСкачать

Момент инерцииСкачать

Некоторые теоремы динамики механической системыСкачать

Физика - импульс и закон сохранения импульсаСкачать

Теоретическая механика.Теорема об изменении количества движения.Кинетический момент(момент импульса)Скачать

Геометрия масс. Теорема о движении центра массСкачать

Общее уравнение динамики. Расчет механической системы.Скачать

Урок 79. Центр масс тела и методы определения его положенияСкачать