- Пространственная система сил
- Пространственная система сходящихся сил
- Разложение силы по трем осям координат
- Аналитический способ определения равнодействующей пространственной системы сходящихся сил
- Аналитические условия равновесия пространственной системы сходящихся сил
- Момент силы относительно оси
- Аналитические условия равновесия пространственной системы произвольно расположенных сил
- Теорема о моменте равнодействующей относительно оси (теорема Вариньона)
- iSopromat.ru
- Решение задач, контрольных и РГР
- Набор студента для учёбы
- Плоская система сил в теоретической механике
- Случай приведения к равнодействующей силе
- Случай приведения к паре сил
- Теорема о моменте равнодействующей силы (Теорема Вариньона)
- Различные формы условий равновесия плоской системы сил
- Теорема о трех моментах (вторая форма условий равновесия)
- Третья форма условий равновесия
- Статически определимые и статически неопределимые задачи
- Равновесие системы тел
- Распределенные силы
- Параллельные силы постоянной интенсивности, распределенные по отрезку прямой линии
- Параллельные силы, распределенные по отрезку прямой с интенсивностью, изменяющейся по линейному закону
- Реакция заделки
- Решение задач на равновесие плоской системы сил, приложенных к твердому телу и системе тел
- Пример 1.
- Пример 2.
- Теорема Вариньона
- Задача 1.
- Задача 2.
- Задача 4.
- Задача 5.
- Задача 6.
- Задача 7.
- Задача 8.
- Задача 9.
- Равновесие произвольной плоской системы сил
- Задача 10.
- Задача 11.
- Задача 12.
- Задача 13.
- Задача 14.
- Задача 15.
- Задача 16.
- Задача 17.
- Задача 18.
- Справочный материал по статике
- Плоская система сходящихся сил
- Простая стержневая система
- Равновесие цепи
- Задача 19.
- Теорема о трех силах
- Задача 20.
- 📸 Видео
Видео:§4.3. Главный вектор и главный момент сил инерцииСкачать

Пространственная система сил
Пространственная система сходящихся сил
Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил .
Пространственная система сил называется сходящейся , если линии действия всех сил системы пересекаются в одной точке.
Теорема: пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Пусть дана пространственная система n сходящихся сил (F1, F2, F3. Fn) . На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма последовательно сложим все силы и получим их равнодействующую:
Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей пространственной системы сходящихся сил неприемлемы, а применяется только аналитический способ (метод проекций) .
Проекция силы на ось в пространстве находится по проецирующим перпендикулярам, и может быть определена при помощи тригонометрических функций. При определении проекций сил пространственной системы потребуется система координат с осями X , Y , Z , поскольку силы системы не располагаются в одной плоскости.
Правило знаков для проекций будет таким же, как и для плоской системы сил – совпадающие по направлению с координатной осью силы считаются положительными, в противном случае – отрицательными. Если вектор силы параллелен какой-либо оси координат, то он проецируется на эту ось в натуральную величину, если же вектор перпендикулярен оси, его проекция на эту ось будет равна нулю.
Разложение силы по трем осям координат
Пусть дана сила F (см. рисунок 1) .

Достроим полученное изображение до параллелепипеда, у которого составляющие Fx , Fy и Fz являются ребрами, а сила F – диагональю.
Из изложенного можно сделать вывод: равнодействующая трех взаимно-перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах .
Из рисунка видно, что в случаях разложения силы F по трем взаимно-перпендикулярным направлениям x , y , z составляющие Fx , Fy и Fz равны по модулю проекциям силы F на эти оси.
Зная проекции силы на три взаимно-перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:
модуль силы: F = √(Fx 2 + Fy 2 + Fz 2 ) (здесь и далее √ — знак корня) ;
направляющие косинусы: cos(F,x) = Fx/F; cos(F,y) = Fy/F; cos(F,z) = Fz/F .
Аналитический способ определения равнодействующей пространственной системы сходящихся сил
Рассмотренный выше способ разложения силы F на три составляющие по направлению координатных осей x , y , z можно применить для каждой из сходящихся сил пространственной системы. Тогда вместо данной системы n сходящихся сил мы получим эквивалентную ей систему 3n сил, из которых n сил действуют по оси x , n сил – по оси y , и n сил – по оси z .
Равнодействующая проекций сил системы на ось x равна их геометрической сумме, то же самое можно сказать и о равнодействующих проекций сил на оси y и z .
Таким образом, систему 3n сил можно заменить эквивалентной ей системой трех сил, каждая из которых представляет собой равнодействующую проекций сил данной системы на ту или иную ось координат.
Проекции силы на три взаимно-перпендикулярные оси и составляющие силы, направленные по этим осям, равны по модулю, следовательно, проекции равнодействующей равны:
Очевидно, что равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах, и по известным проекциям равнодействующей можно определить модуль и направление самой равнодействующей.
Аналитические условия равновесия пространственной системы сходящихся сил
Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система сил находится в равновесии, т. е. эквивалентна нулю, то можно сделать вывод, что равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей тоже равны нулю, причем эти проекции равны сумме проекций составляющих.
Отсюда вытекают условия равновесия пространственной системы сходящихся сил:
ΣX = 0; ΣY = 0; ΣZ = 0 .
Эти условия формируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую их трех координатных осей равнялась нулю.
Момент силы относительно оси
Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (см. рисунок 2) . Червяк передает червячному колесу силу F , не лежащую в плоскости, перпендикулярной оси.
Разложим силу F на три взаимно-перпендикулярные составляющие F1 , F2 и F3 .
Составляющую F1 назовем окружной силой , составляющую F2 – осевой силой , а составляющую F3 – радиальной силой .
Из рисунка видно, что составляющая F1 вызывает вращательное действие, которое измеряется произведением силы F1 на радиус колеса r ; составляющая F2 стремится сдвинуть червячное колесо вдоль оси, а составляющая F3 стремится изогнуть ось колеса.
Очевидно, что вращающее действие сил F2 и F3 относительно оси колеса равно нулю.
Таким образом, если нужно найти момент силы относительно оси, то следует принимать в расчет только составляющую F1 , лежащую в плоскости, перпендикулярной оси, и не пересекающую ось (иначе ее момент будет равен нулю).
Ранее было отмечено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением.
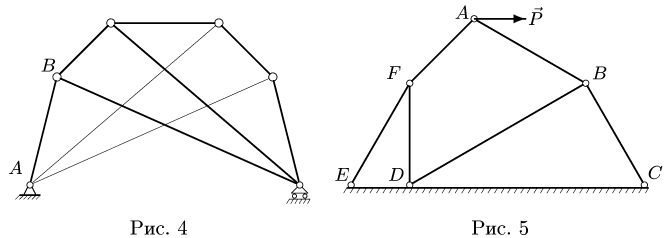
Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Это определение поясняет рисунок 3 .
Момент силы относительно оси условимся записывать следующим образом:
Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, если же сила стремится вызвать вращение по часовой стрелке, ее момент считаем отрицательным.
Момент силы относительно оси не меняется при перемещении силы вдоль оси ее действия.
Момент силы будет равен нулю в двух случаях (не считая случаев, когда сила равна нулю или направлена вдоль оси):
- если вектор силы параллелен оси, так как при этом проекция силы на плоскость, перпендикулярную оси, равна нулю (см. рисунок 3, сила FZ) ;
- если линия действия силы пересекает ось, так как при этом плечо равно нулю (сила F3 на рисунке 2) .
Аналитические условия равновесия пространственной системы произвольно расположенных сил
Пространственная система сил, в которой линии действия составляющих сил расположены произвольно, т. е. линии их действия могут не пересекаться и находиться в разных плоскостях, называется произвольно расположенной системой сил.
Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю.
Строгое обоснование приведенного выше условия равновесия пространственной системы произвольно расположенных сил требует знания некоторых вопросов, не предусмотренных программами учреждений среднего профессионального образования, поэтому условие равновесия такой системы здесь приводится без доказательства.
Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:
- ΣX = 0; ΣMx(Fi) = 0;
- ΣY = 0; ΣMy(Fi) = 0;
- ΣZ = 0; ΣMz(Fi) = 0.
Свободное тело в пространстве имеет шесть степеней свободы, а именно: возможность перемещаться в направлениях трех взаимно-перпендикулярных осей координат и возможность вращаться вокруг этих осей. Таким образом, шести степеням свободы тела в пространстве соответствуют шесть условий равновесия.
Если система сил, приложенных к свободному телу, удовлетворяет всем шести условиям равновесия, то возможность трех перемещений и трех вращений тела под действием сил системы исключена, поэтому тело будет находится в равновесии.
Очевидно, что все выведенные ранее условия равновесия для различных систем сил являются частными случаями условия равновесия пространственной системы произвольно расположенных сил.
Так как условия равновесия пространственной системы сил справедливы для любых прямоугольных осей координат, то при решении данной задачи систему координат можно изменять, т. е. часть уравнений равновесия составить для одних осей координат, а часть – для измененных. В некоторых случаях этот прием упрощает решение задач.
Теорема о моменте равнодействующей относительно оси
(теорема Вариньона)
Теорема: момент равнодействующей относительно оси равен алгебраической сумме моментов, составляющих сил относительно этой же оси .
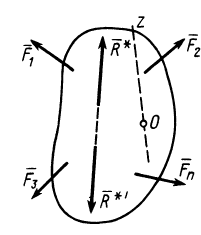
Пусть даны пространственная система n произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы сил FΣ (см. рисунок 4) :
Приложим к телу другую систему сил, равнодействующая которой F’Σ по модулю равна FΣ и направлена по той же линии действия, но в противоположную сторону, т. е. является уравновешивающей данной системы сил.
Тогда можно записать:
Так как обе записанные выше системы сил эквивалентны нулю, т. е. уравновешены, то к ним можно применить любое условие равновесия, например
Запишем это условие для обеих систем:
Так как правые части этих равенств равны, то будут равны и левые :
Сократив общее слагаемое Mx(F’Σ) , получим:
Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

iSopromat.ru
Теорема Вариньона гласит: момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.
В некоторых случаях при определении момента силы возникают трудности в расчете плеча силы.
Теорема Вариньона значительно упрощает решение этого вопроса.
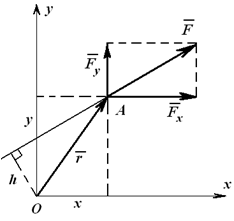
Например, момент силы F относительно точки O можно определить как алгебраическую сумму моментов сил Fx и Fy (на которые можно разложить силу F) относительно той же точки O (рисунок 1.17). То есть
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Момент силы относительно точки и осиСкачать

Решение задач, контрольных и РГР
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
Видео:Теорема Вариньона о моменте равнодействующейСкачать

Набор студента для учёбы
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Видео:2.2. Главный вектор и главный момент плоской системы сил. Приведение к простейшему видуСкачать
Плоская система сил в теоретической механике
Содержание:
Плоская система сил:
Плоскую систему сил можно привести к более простой системе сил, состоящей из силы или пары сил. Эти случаи возможны, если система сил не находится в равновесии, т. е. если одновременно не равны нулю главные вектор и момент системы сил. Рассмотрим эти частные случаи.
Видео:Основная теорема статикиСкачать

Случай приведения к равнодействующей силе
- Если при приведении плоской системы сил к какому-либо центру окажется, что главный вектор
Равнодействующая сила
в этом случае проходит через центр приведения, а по величине и направлению совпадает с главным вектором
.
- Если при приведении плоской системы сил главный вектор
и главный момент
, то такую систему можно упростить и привести к одной равнодействующей силе
.
Эта сила по величине и направлению совпадает с главным вектором 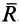
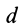
Рис. 40
Действительно, пусть при приведении к точке 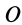
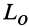
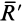
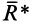
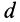
Повернем пару сил, чтобы ее силы были параллельны главному вектору 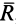
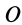
Так как 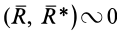
Итак, систему сил, приведенную к силе с парой сил, в том случае, когда 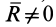
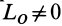
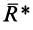
Равнодействующую силу 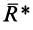
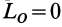
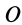
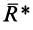
Видео:Приведение системы сил к простейшему видуСкачать

Случай приведения к паре сил
Если при приведении плоской системы су л к какому-либо центру окажется, что главный вектор 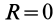
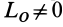
Если главный вектор равен нулю при приведении к одному какому-либо центру, то он равен нулю и при приведении к любому другому центру, так как главный вектор, являясь векторной суммой сил системы, не зависит от выбора центра приведения. Главный момент не зависит от центра приведения только в том случае, когда 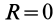
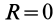
Таким образом, рассмотрены случаи, которые возможны при приведении плоской системы сил к какому-либо центру. Если 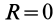
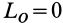
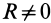
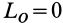
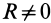
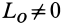
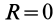
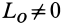
Теорема о моменте равнодействующей силы (Теорема Вариньона)
Для случая, когда любая система сил, приложенных к твердому телу, плоская или пространственная, приводится к равнодействующей силе, часто применяют так называемую теорему Вариньона: векторный момент равнодействующей рассматриваемой системы сил относительно любой точки равен сумме векторных моментов всех сил этой системы относительно той же точки.
Рис. 41
Пусть на твердое тело действует любая система сил 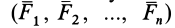
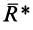
Добавим к заданной системе сил ее уравновешивающую силу 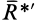
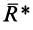
т.е. при добавлении к системе сил уравновешивающей силы, согласно определению уравновешивающей силы, образуется новая система сил, эквивалентная нулю и, следовательно, удовлетворяющая условиям равновесия системы сил, приложенных к твердому телу. В частности, сумма векторных моментов сил этой новой системы сил относительно любой точки 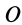
так как 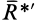
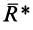
откуда следует теорема Вариньона
Если правую и левую части векторного равенства (6) спроецировать на произвольную ось 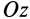
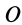
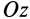
т. е. момент равнодействующей силы относительно произвольной оси равен сумме моментов сил системы относительно той же оси.
Для случая плоской системы сил, если точку 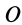
Это теорема Вариньона для плоской системы сил: алгебраический момент равнодействующей плоской системы сил относительно любой точки, лежащей в плоскости действия сил, равен сумме алгебраических моментов всех сил этой системы относительно той же точки.
Различные формы условий равновесия плоской системы сил
Получены общие условия равновесия плоской системы сил, действующих на твердое тело, в следующей форме:
Условия равновесия (9) назовем условиями равновесия плоской системы сил в первой форме.
Условия равновесия плоской системы сил, приложенных к твердому телу, можно сформулировать в других эквивалентных формах. Существуют еще две эквивалентные формы необходимых и достаточных условий равновесия.
Рассмотрим эти условия равновесия в виде теоремы о трех моментах и третьей формы условий равновесия.
Теорема о трех моментах (вторая форма условий равновесия)
Для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю, т. е.
Необходимость этих условий равновесия плоской системы сил обусловлена тем, что если плоская система сил находится в равновесии, то силы этой системы удовлетворяют условиям равновесия в первой основной форме (9). А тогда из последнего условия (9) следует, что сумма алгебраических моментов сил относительно любой точки (следовательно, и точек 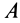
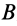
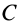
Для доказательства достаточности условий (10) для равновесия плоской системы сил, действующих на твердое тело, можно привести следующие рассуждения. Так как главные моменты относительно трех точек 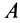
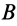
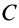
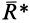
Рис. 42
Выбрав за центр приведения точку 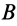
Эти условия для равнодействующей силы 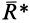
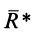
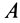
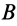
Из последнего условия (10) после применения теоремы Вариньона получаем
Но 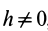
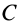
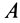
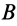
Третья форма условий равновесия
Условия равновесия плоской системы сил можно сформулировать и так: для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил относительно двух любых точек, лежащих в плоскости действия сил, были равны нулю и алгебраическая сумма проекций этих сил на какую-либо ось плоскости, не перпендикулярную прямой, проходящей через две моментные точки, также была равна нулю, т. е.
где за ось 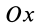
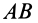
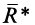
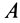
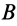
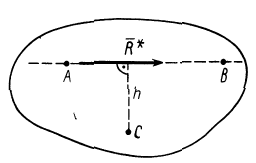
Из последнего условия (11) (рис.43) следует, что
так как ось 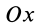
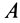
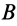
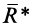
В частном случае плоской системы параллельных сил можно сформулировать другую форму условий равновесия этой системы сил: для равновесия плоской системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил относительно двух любых точек, лежащих в плоскости сил, были равны нулю, т. е.
Точки 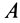
При применении условий равновесия (12) удобно за момент-ные точки 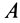
Рис. 43
Видео:Приведение системы сил к простейшему видуСкачать

Статически определимые и статически неопределимые задачи
Для любой плоской системы сил, действующих на твердое тело, имеется только три независимых условия равновесия, каждое из которых не является следствием двух других. Независимые условия равновесия можно брать в трех различных формах.
Следовательно, для любой плоской системы сил из условий равновесия можно найти не более трех неизвестных, а для плоских систем параллельных и сходящихся сил — не более двух неизвестных. Если в какой-либо задаче число неизвестных окажется больше числа независимых условий равновесия, то такую задачу нельзя решить методами статики без рассмотрения прежде всего деформаций тела, т. е. без отказа от основной гипотезы статики об абсолютно твердом теле.
Задачи, в которых число неизвестных не больше числа независимых условий равновесия для данной системы сил, приложенных к твердому телу, называют статически определимыми. Для любой плоской системы сил, приложенных к твердому телу, в статически определимой задаче число неизвестных должно быть не больше трех, а для плоских систем параллельных и сходящихся сил — не больше двух.
Пример простейшей статически неопределимой задачи приведен на рис. 44, где представлена балка заданной длины, закрепленная на концах с помощью двух неподвижных цилиндрических шарниров 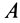
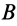
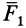
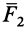
Чтобы сделать задачу статически определимой, надо балку на одном конце закрепить, например с помощью так называемой катко-вой опоры. Тогда одна неизвестная будет равна нулю; если катковая опора находится в точке 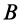
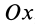
Рис. 44
Равновесие системы тел
Рассмотрим равновесие сил, приложенных к системе нескольких взаимодействующих между собой тел. Тела могут быть соединены между собой с помощью шарниров, соприкасаться друг с другом и взаимодействовать одно с другим, вызывая силы взаимодействия. Такую систему взаимодействующих тел иногда называют сочлененной системой тел.
Силы, действующие на рассматриваемую систему тел, можно разделить на внешние и внутренние.
Внешними называют силы, с которыми на тела рассматриваемой системы действуют тела, не входящие в эту систему.
Внутренними называют силы взаимодействия между телами рассматриваемой системы.
Если, например, рассматриваемой системой тел является железнодорожный поезд, то внешними силами являются силы веса вагонов и тепловоза, действие рельсов на колеса вагонов и тепловоза, силы сопротивления воздуха. Внутренними силами являются натяжения в стяжках, сила давления газа и т. п.
Силы веса для любой системы тел, в которую не входит Земля, всегда являются внешними.
При рассмотрении равновесия сил, приложенных к системе тел, можно мысленно расчленить систему тел на отдельные твердые тела и к силам, действующим на эти тела, применить условия равновесия, полученные для одного тела. В эти условия равновесия войдут как внешние, так и внутренние силы системы тел. Внутренние силы на основании аксиомы о равенстве сил действия и противодействия в каждой точке сочленения двух тел образуют равновесную систему сил (силы 
Рис. 45
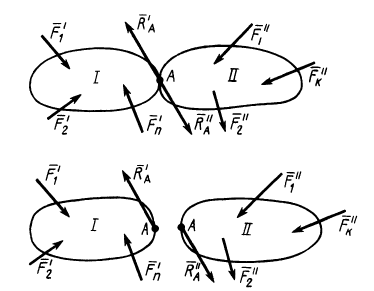
Покажем это на примере системы двух тел и плоской системы сил (рис. 45). Если составить условия равновесия для каждого твердого тела системы тел, то для тела
для тела
Кроме того, из аксиомы о равенстве сил действия и противодействия для двух взаимодействующих тел имеем
Если сложить (13) и (14), учитывая (15 и (16), то
Представленные равенства и есть условия равновесия внешних сил, действующих на систему двух тел.
Для системы 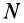
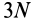
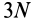
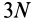
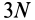
Распределенные силы
В статике рассматривают силы, приложенные к твердому телу в какой-либо его точке, и поэтому такие силы называют сосредоточенными. В действительности обычно силы бывают приложены к какой-либо части объема тела или его поверхности, а иногда к некоторой части линии. Так как все аксиомы и теоремы статики формулируются для сосредоточенных сил, приложенных к твердому телу, то необходимо рассмотреть способы перехода от распределенных сил к сосредоточенным в простейших, наиболее часто возникающих случаях.
Распределенные силы прежде всего характеризуются интенсивностью распределенной силы, т.е. силой, приходящейся на единицу объема, поверхности или длины линии. В основном встречаются параллельные и сходящиеся распределенные силы. К параллельным силам, распределенным по объему тела, относится вес частиц этого тела. Сила давления воды на плотину относится к распределенным параллельным силам по поверхности плотины. Сила тяжести частиц тонкой проволоки характеризует распределенные силы по длине линии.
Рассмотрим замену сосредоточенными силами только распределенных сил по длине линии, т. е. линейных распределенных сил. Для простоты возьмем случаи, когда отрезок линии, по которому распределены силы, является отрезком прямой, а интенсивность этих сил или постоянна (силы распределены по прямоугольнику), или распределена по линейному закону, в простейшем случае — по треугольнику. Комбинируя эти два случая, можно получить линейное распределение интенсивности распределенной силы в более общем случае.
Параллельные силы постоянной интенсивности, распределенные по отрезку прямой линии
Пусть на участке 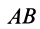
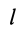
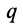
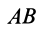
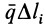
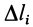
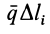
Рис. 46
Равнодействующая 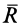
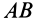
Если параллельные силы постоянной интенсивности 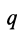
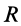
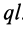
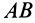
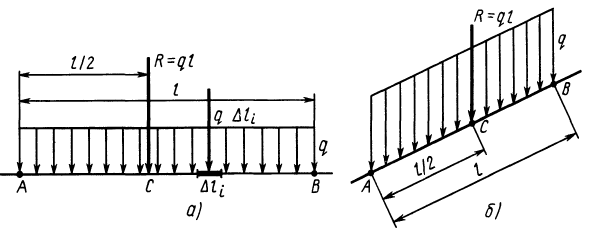
Параллельные силы, распределенные по отрезку прямой с интенсивностью, изменяющейся по линейному закону
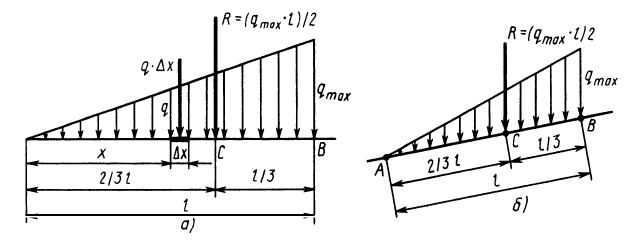
Рассмотрим распределенные параллельные силы, изменяющиеся по линейному закону (рис. 47, а). Обычно считают, что такие силы распределены по треугольнику. Параллельные распределенные по треугольнику силы приводятся к равнодействующей 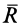
где 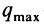
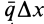
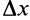
Рис. 47
Если 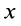
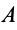
После этого, вставляя под интеграл вместо 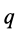
Точка приложения 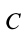
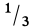
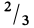
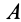
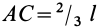
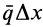
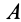
Заменяя 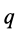
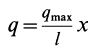
Учитывая, что 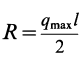
Если параллельные силы с интенсивностью, изменяющейся по линейному закону, распределены по отрезку прямой, наклоненному к направлению сил (рис. 47, б), то их равнодействующая 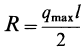
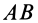
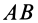
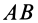
В более сложных случаях распределенных сил равнодействующую силу и ее точку приложения обычно определяют путем интегрирования и применения теоремы Вариньона. Величину равнодействующей в случае непараллельных распределенных сил находят так же, как и для параллельных, только суммируют (и, следовательно, интегрируют) не элементарные сосредоточенные силы 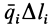
Реакция заделки
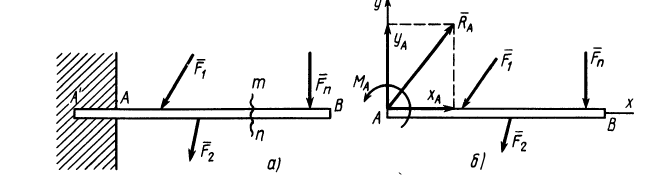
Пусть имеем тело, например балку 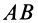
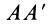
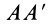
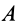
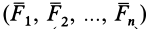
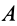
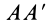
К части балки 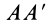
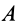
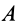
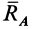
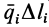
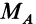
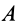
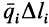
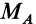
Таким образом, заделка в отличие от шарнира создает не только не известную по величине и направлению реакцию 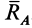
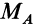
Очевидно, если рассмотреть любую часть балки, расчленив ее мысленно по сечению 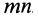
Рис. 48
Решение задач на равновесие плоской системы сил, приложенных к твердому телу и системе тел
Рассмотрим общие положения о решении задач на равновесие плоской системы сил, действующих на одно твердое тело и на систему тел. Весь процесс решения задачи на равновесие сил можно расчленить на ряд этапов, которые характерны для большинства задач.
К выбранному для рассмотрения телу или системе тел надо приложить все действующие силы, как активные, так и реакции связей; если нужно, расчленить систему тел на отдельные тела или группы тел. Если связью является абсолютно гладкая поверхность какого-либо тела, то реакция связи в этом случае направлена по нормали к общей касательной в точке соприкосновения в сторону, противоположную тому направлению, в котором связь препятствует перемещению рассматриваемого тела.
Если связью является цилиндрический шарнир, позволяющий телу вращаться вокруг его оси, то реакцию шарнира, лежащую в плоскости, перпендикулярной оси, следует разложить на две заранее не известные составляющие по положительным направлениям осей координат. Если эти составляющие после их определения из уравнений равновесия будут иметь знак минус, то составляющие реакции направлены противоположно положительному направлению осей координат.
Все гибкие связи (канаты, тросы, ремни и т. п.) создают реакции, направленные по касательной к гибкой связи в данной точке.
Если связью является заделка, которая в отличие от цилиндрического шарнира не позволяет телу поворачиваться, то кроме двух неизвестных составляющих реакций в этой точке надо еще приложить пару сил с не известным заранее моментом заделки.
Эти же случаи связей возможны и при расчленении систем тел.
Выявление всех сил, действующих на рассматриваемое тело или систему тел, особенно правильная замена различных видов связей их реакциями, является одним из главных этапов при решении задач на равновесие.
При расчленении системы тел надо следить, чтобы силы взаимодействия между телами или группами тел сочленной системы в точках сочленения были равны по модулю, но противоположны по направлению. При рассмотрении системы тел (или их группы) силы взаимодействия между телами системы (или их группы) прикладывать не нужно, так как эти силы являются внутренними и в уравнения равновесия для системы тел (или группы) не войдут.
Рис. 49
После выявления всех сил надо выбрать оси координат и моментные точки, а затем, составив условия равновесия сил в одной из форм, решить полученные уравнения относительно неизвестных.
Решение уравнений будет более простым, если при их составлении в каждое из уравнений добавляется по одной новой неизвестной. Этого удается достичь, если за моментную точку брать такую, в которой пересекаются две искомые силы. Такой точкой обычно является цилиндрический шарнир. Оси координат надо брать так, чтобы одна или две неизвестные силы были перпендикулярны одной из осей координат и, следовательно, параллельны другой оси. В этом случае в соответствующее условие равновесия для одного тела войдет только одна неизвестная сила.
Приведем примеры решения задачи на плоскую систему сил.
Пример 1.
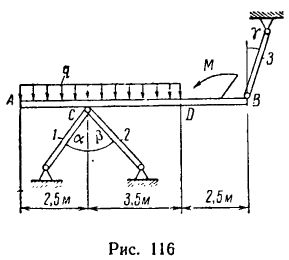
Дана система двух твердых тел, соединенных с помощью шарнира 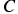
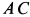
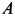
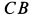
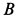
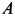
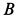
Решение. Заменим распределенные силы сосредоточенными. Величина равнодействующей силы 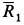
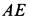
Точка приложения силы 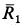
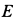
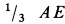
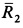
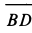
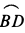
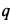
Рис. 50
Линия действия равнодействующей силы 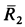
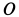
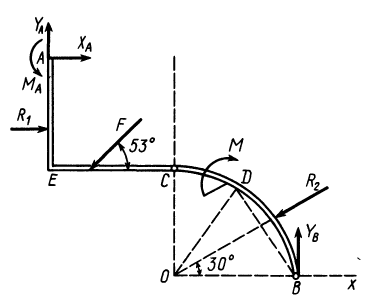
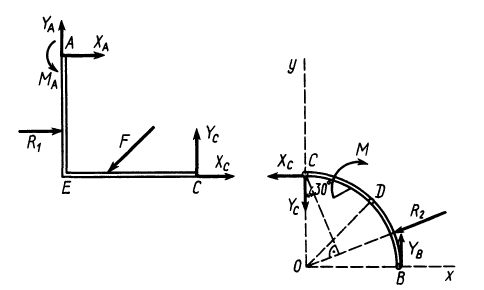
Рассмотрим сначала равновесие системы двух тел, состоящих из балки 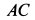
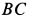
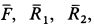
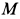
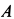
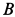
Реакции заделки в точке 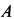
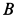
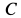
В дальнейшем целесообразно на рисунках у стрелок, изображающих силы, ставить только буквы, обозначающие значения сил, без знака вектора над ними (рис. 51). Это уменьшит число неизвестных и, следовательно, количество уравнений для их определения.
Всего имеется шесть неизвестных, считая составляющие силы реакции в шарнире 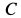
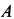
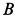
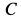
Рис. 51
Составим для арки 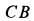
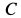
откуда получаем 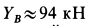
После этого для всей системы тел применим условие равновесия в форме суммы проекций сил на оси 
откуда 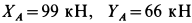
Для определения момента пары сил 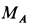
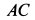
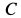
откуда 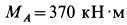
Если дополнительно требуется определить силы 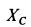
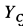
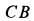
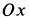
Из этих уравнений получаем
Для контроля правильности определения реакций в точках 
Задача считается решенной, если известны проекции искомых сил на оси координат, так как по проекциям легко определяются модули этих сил и косинусы углов сил с осями координат.
Пример 2.
Для системы тел, находящихся в равновесии, определить реакцию шарнира 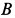
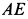
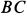
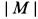
Рис. 52
Решение. Рассмотрим всю систему тел, освободив ее от связей, т.е. от цилиндрических шарниров в 
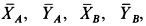
Для определения 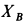
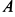
откуда 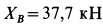
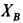
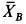
Рис. 53
Другие условия равновесия сил для всей системы тел не позволяют определить неизвестную 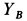
Рассмотрим отдельно равновесие стержня 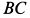
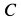
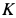
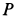
Для определения 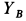
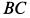
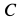
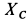
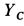
Отсюда находим 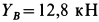
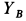
Для приобретения опыта силового анализа в системах тел рассмотрим дополнительно еще несколько вариантов частей системы тел и отдельных тел с приложенными к ним силами (рис. 54. 57).
Рис. 54
Рис. 55
Рис. 56
Рис. 57
При замене отбрасываемых тел силами учтено, что оси блоков 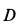
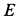
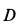
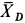
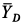
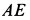
При отбрасывании нити следует учитывать, что ее натяжение во всех точках при отсутствии трения в осях блоков одинаково по величине и направлено по касательной к нити. Нить при этом должна испытывать только растяжение. При рассмотрении отдельного блока силы натяжения нитей следует приложить в двух точках, в которых отбрасываются части нити.
Теорема Вариньона
Из формулы, определяющей расстояние от центра приведения до линии действия равнодействующей,
(см. рис. 74) можно вывести уравнение, выражающее теорему Вариньона для произвольной плоской системы сил: 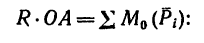
момент равнодействующей относительно любой точки равен алгебраической сумме моментов заданных сил относительно той же точки.
Теорема Вариньона находит широкое применение при решении задач по статике, в частности во всех тех задачах, где рассматривается равновесие рычага.
При помощи теоремы Вариньона очень просто определяется равнодействующая какого угодно числа параллельных сил 
Известно, что модуль равнодействующей любой плоской системы сил равен модулю главного вектора:
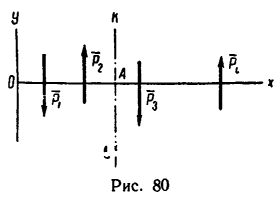
Но если в данном случае расположить оси проекции так, как показано на рис. 80, одну ось — перпендикулярно к силам, а другую—параллельно им, то
Таким образом, модуль равнодействующей, параллельной системы сил равен абсолютному значению алгебраической суммы проекций сил на ось, параллельную этим силам.
Так как 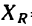
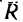
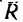
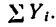
Определив модуль и направление равнодействующей, по теореме Вариньона находим расстояние ОА, на котором расположена
KL- линия действия R от произвольно выбранного центра моментов О.
Задача 1.
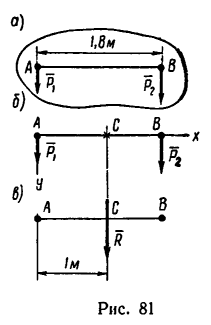
Определить равнодействующую двух параллельных сил 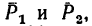
1. Примем за начало осей проекций точку А. Ось х расположим перпендикулярно к данным силам и направим ее вправо, а ось у направим вдоль силы 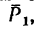
2. Найдем модуль равнодействующей:
Так как сумма проекций положительна, то вектор равнодействующей направлен тоже вниз.
3. Приняв за центр моментов точку А, найдем расстояние АС от точки A до линии действия равнодействующей.
В данном случае
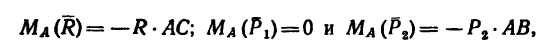
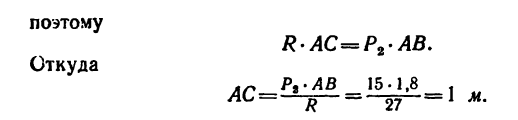
Таким образом, равнодействующая двух данных сил численно равна 27 н, и линия ее действия расположена от точки А на расстоянии АС = 1 м (рис. 81, в).
Задача 2.
Найти равнодействующую двух параллельных сил 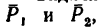
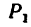
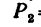
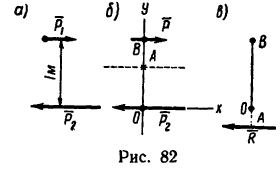
1. Расположим оси Ох и Оу так, как показано на рис. 82, б.
2. Найдем модуль равнодействующей:
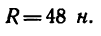
Сумма проекций заданных сил имеет отрицательное значение. Следовательно, равнодействующая направлена влево (ось Ох направлена вправо).
3. Приняв за центр моментов точку О и предположив, что линия действия R пересекает отрезок ОВ в точке А, составим уравнение
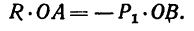
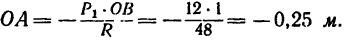
Числовое значение О А получается отрицательным, значит этот отрезок от точки О необходимо отложить в противоположную сторону от ранее предполагаемого.
Равнодействующая заданных сил численно равна 48 и, направлена влево, и линия ее действия лежит ниже точки О на 0,25 м (рис. 82, в).
Задача 3.
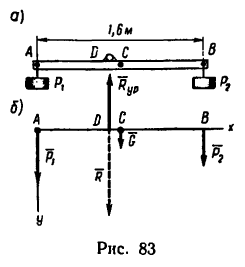
К концам прямолинейной однородной планки длиной 1,6 м и весом 5 н прикреплены два груза (рис. 83): слева —груз 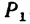
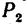
1. Изобразим на рис. 83 в горизонтальном положении планку АВ с грузами 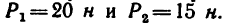
Таким образом, к планке приложена система трех параллельных сил, действующих в одну сторону (рис. 83, б).
2. Оси проекций расположим, как показано на рис. 83, б.
3. Найдем модуль равнодействующей сил
Равнодействующая направлена вертикально вниз.
4. Определим, на каком расстоянии AD от точки А (левого конца планки) расположена линия действия равнодействующей:
Линия равнодействующей проходит через точку D на расстоянии 0,7 м от левого конца планки.
В этом месте и необходимо прикрепить к планке петельку. Если теперь за петельку подвесить планку на гвоздь или прикрепить к нити, то планка будет находиться в равновесии, оставаясь горизонтальной, так как равнодействующая R уравновесится реакцией 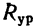
Задача 4.
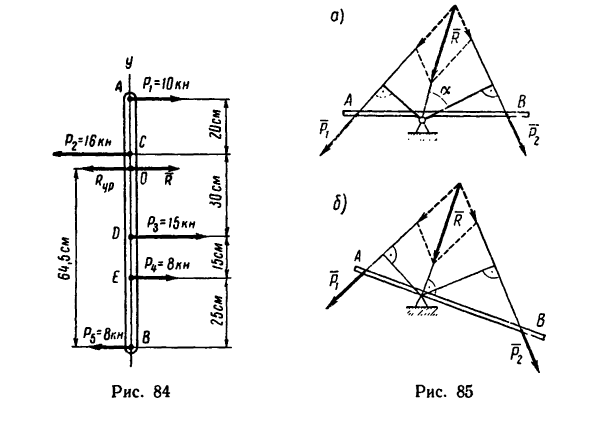
Балансир АВ, на который действуют пять горизонтально направленных параллельных сил (рис. 84), должен находиться в равновесии в вертикальном положении, будучи насаженным на горизонтальную ось.
Определить, где необходимо поместить ось балансира, пренебрегая его весом.
1. Расположив оси проекций, как указано на рис. 84, найдем модуль равнодействующей системы параллельных сил:
Таким образом, равнодействующая направлена вправо.
2. Определим расстояние ВО от нижнего конца балансира до линии действия 
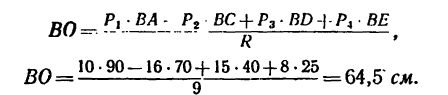
Следовательно, линия действия равнодействующей пересекает находящийся в вертикальном положении балансир на расстоянии 64,5 см от нижнего конца В. Здесь (в точке О) и нужно поместить ось балансира.
Следующую задачу рекомендуется решить самостоятельно.
Задача 5.
Где необходимо поместить ось балансира, описанного в предыдущей задаче, если силу 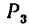
Ответ. ВО = 29,5 см.
Задачи, приведенные ниже, решаются при помощи так называемого условия равновесия рычага, непосредственно вытекающего из теоремы Вариньона.
Рычагом можно назвать любое тело, поворачивающееся либо вокруг закрепленной оси, либо около линии контакта, образующейся при свободном направлении на другое тело.
Находясь под действием сил, рычаг уравновешен лишь в том случае, если линия действия равнодействующей пересекает ось или линию опоры. Причем если опорой рычага АВ служит закрепленная ось (неподвижный шарнир), то линия действия равнодействующей может быть направлена к рычагу под любым углом а (рис. 85, а). Если же рычаг АВ свободно опирается на идеально гладкую опору
(рис. 85, б), то линия действия равнодействующей должна быть перпендикулярна к опорной поверхности.
В любом нз этих случаев равновесие возникает потому, что система сил, действующих на рычаг, уравновешивается реакцией опоры 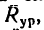
выражающее условие равновесия рычага.
Задача 6.
Масса неоднородного стержня составляет 4,5 кг. Для определения положения центра тяжести стержня его левый конец положен на гладкую опору, а правый зацеплен крюком динамометра (рис. 86, а). При горизонтальном положении стержня динамометр показывает усилие 1,8 кГ. Расстояние АВ —130 см от левой опоры до динамометра определено путем непосредственного измерения. Определить ^положение центра тяжести стержня.
1. Рассмотрим стержень как рычаг с опорой в точке А. Кроме реакции опоры, на него действуют две нагрузки: вес G = 4,5 кГ (1 кг массы притягивается к земле силой, равной 1 кГ), приложенный в центре тяжести на искомом расстоянии х от опоры А, и усилие пружины динамометра Я = 1,8 кГ (рис. 86, б).
2. Составим уравнение равновесия рычага:
В данном случае относительно точки А моменты создают две силы 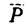
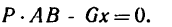
Решаем полученное уравнение: 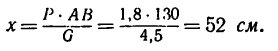
Центр тяжести стержня расположен на расстоянии 52 см от левой опоры.
Задача 7.
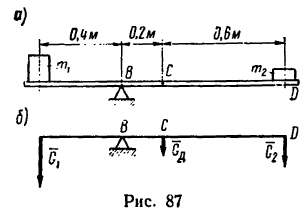
Какова должна быть масса однородной доски (рис. 87, а), чтобы, опираясь в точке В на гладкую опору, она с положенными на нее грузами 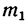
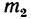
1. Рассматривая доску как рычаг, видим, что на нее действуют гри нагрузки: вес левого груза 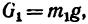
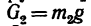
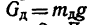
2. Для равновесия доски необходимо, чтобы алгебраическая сумма моментов этих сил относительно опоры В равнялась нулю. Следовательно,
3. Подставив вместо весов их выражения через массы и разделив обе части равенства на постоянную величину g (ускорение свободного падения 9,81 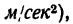
4. Отсюда находим массу доски:
Масса доски 8 кг.
Задача 8.
Предохранительная заслонка открывается в тот момент, когда давление в резервуаре превышает внешнее атмосферное на р=150 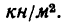
На каком расстоянии х от опоры рычага необходимо поместить груз весом G = 120 н, чтобы заслонка открылась при заданном давлении, если площадь отверстия в резервуаре 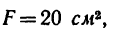
1. На рычаг АВС предохранительного устройства действуют две нагрузки: вес груза G = 120 н и сила Р, открывающая заслонку:
2. Условие равновесия рычага выразится уравнением
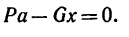
3. Решая это уравнение, находим 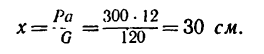
Груз необходимо поместить на расстоянии 30 см от опоры В.
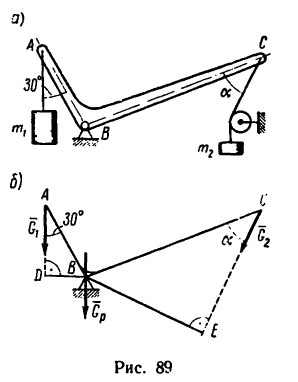
Задача 9.
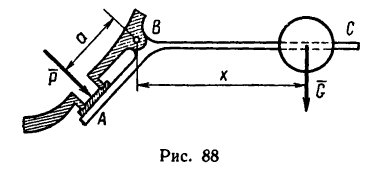
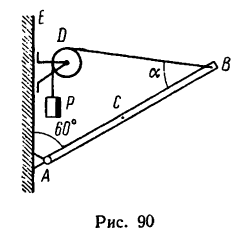
На рис. 89, а изображен коленчатый рычаг АВС, к короткому колену которого при помощи нити прикреплен груз массой 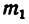
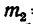
Под каким углом а к длинному колену необходимо расположить вторую нить, чтобы нить, удерживающая первый груз, образовала с АВ угол 30°? Расстояния
Считать, что при этом положении рычага линия действия собственного веса рычага 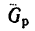
1. На рис. 89, б изобразим расчетную схему рычага; к точке А отвесно приложен вес первого груза 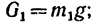
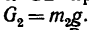
2. Замечая, что 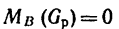
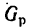
3. Выразив плечи BD и BE через длины колен рычага, а веса 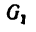
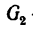
Этому значению sin а соответствует прямой угол. Следовательно,
Поэтому нить, удерживающую второй груз, нужно расположить перпендикулярно к длинному колену рычага.
Следующую задачу рекомендуется решить самостоятельно.
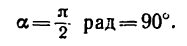
Равновесие произвольной плоской системы сил
Задача на равновесие произвольной плоской системы сил решается по той же общей схеме, которая приведена в § 8-2. Придерживаясь этой схемы, необходимо учитывать следующее.
Как известно, любую плоскую систему сил можно привести к главному вектору 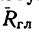
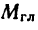
Если же система сил уравновешена (тело, находящееся под действием такой системы сил, либо неподвижно, либо равномерно вращается около неподвижной оси, либо находится в равномерном и прямолинейном поступательном движении), то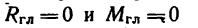
Для произвольной плоской системы сил из этих двух условий непосредственно получаем три уравнения равновесия:
Первое и второе выражения — уравнения проекций — образуются из условия 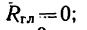
Если на тело действует система параллельных сил, то уравнений равновесия получится только два: уравнение проекций на ось, параллельную силам, и уравнение моментов
При решении некоторых задач одно или оба уравнения проекций целесообразно заменить уравнениями моментов относительно каких-либо точек, т. е. систему уравнений равновесия можно представить в таком виде:
или
В первом случае линия, проходящая через точки А и В, не перпендикулярна к оси х. Во втором случае центры моментов А, В и С не лежат на одной прямой линии.
Для системы параллельных сил соответственно получаем два уравнения моментов:
В этом случае точки А и В не лежат на прямой, параллельной силам.
В задачах, решаемых при помощи уравнений равновесия, обычно рассматриваются тела, находящиеся в состоянии покоя, тогда система сил, действующих на это тело, уравновешена.
Силы, действующие на тело, делятся на две группы. Одна группа сил называется нагрузками (активные силы), вторая группа сил называется реакциями связей (пассивные силы).
Нагрузки, как правило, бывают заданы. Они имеют числовое значение, точку приложения к телу и направление их действия.
В рассматриваемых ниже задачах используются лишь три разновидности нагрузок: сосредоточенные силы, равномерно распределенные силы * и пары сил (статические моменты) **.
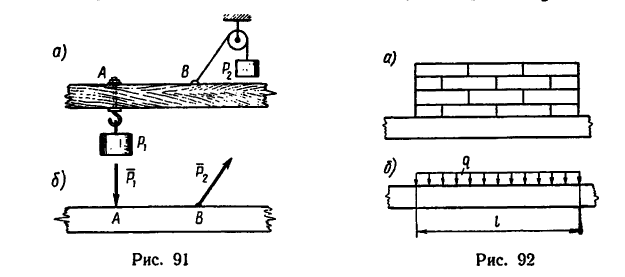
Сосредоточенными называются силы, приложенные к точке тела. Если, например, на тело действуют нагрузки 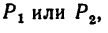
заново на рис. 91, а, действия этих нагрузок можно считать приложенными соответственно к точкам А или В тела и на расчетных схемах изобразить так, как это выполнено на рис. 91, б.
Равномерно распределенные нагрузки, например кирпичная кладка (рис. 92, а), или собственный вес однородного тела (бруса, балки) постоянного поперечного сечения по всей его длине задается при помощи двух параметров —интенсивности q и длины l на протяжении которой они действуют. На расчетных схемах эти нагрузки изображаются так, как показано на рис. 92, б.
* К распределенным нагрузкам относятся также неравномерно распределенные нагрузки, но в настоящем пособии они не рассматриваются.
** Здесь не рассматриваются случаи, когда пары сил действуют на некотором расстоянии непрерывной цепочкой моментов (распределенные моменты).
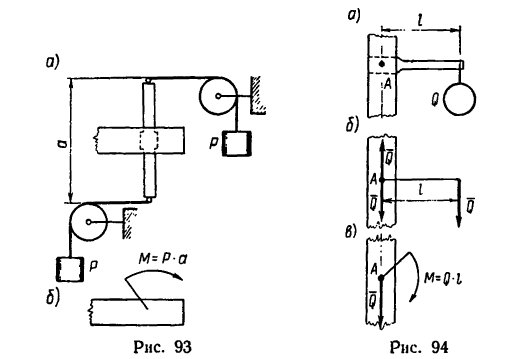
Пара сил (сосредоточенный момент), например, может быть образована двумя одинаковыми грузами Р, действующими на тело так, как показано на рис. 93, а. Условное изображение пары сил, действующей на тело, показано на рис. 93, б.
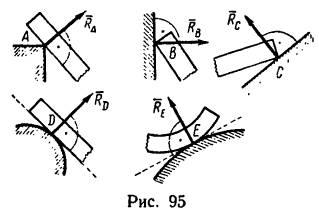
Очень часто в каком-либо месте тела возникает совместное действие сосредоточенной силы и момента. Пусть, например, груз Q подвешен на конце бруса, жестко заделанного другим концом
в каком-либо теле (рис. 94, а). Если перенести действие силы в точку А тела (рис. 94, б), то получим в ней совместное действие сосредоточенной силы и момента.
Как правило, в задачах по статике реакции связей —искомые величины. Для каждой искомой реакции связи обычно необходимо
знать ее направление и числовое значение (модуль).
Направления реакций идеальных связей — связей без трения — определяют в зависимости от вида связи по следующим правилам.
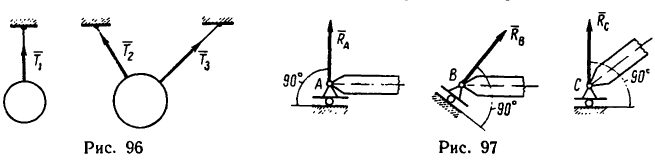
1. При свободном опирании тела на связь реакция связи направлена от связи к телу перпендикулярно либо к поверхности тела 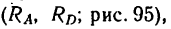
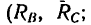
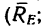
Во всех этих случаях связь препятствует движению тела в одном направлении —перпендикулярном к опорной поверхности.
2. Если связями являются нити, цепи, тросы (гибкая связь), то они препятствуют движению тела только будучи натянутыми.
Поэтому реакции нитей, цепей, тросов всегда направлены вдоль их самих в сторону от тела к связи (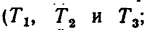
3. Если связь тела с какой-либо опорной поверхностью осуществляется при помощи подвижного шарнира (рис. 97), то его реакция направлена перпендикулярно к опорной поверхности. Таким
образом, подвижный шарнир (т. е. шарнир, ось которого может передвигаться вдоль опорной поверхности) представляет собой конструктивный вариант свободного опирания.
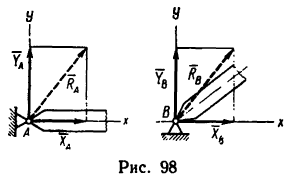
4. Если соединение тела со связью осуществляется при помощи неподвижного шарнира (рис. 98), то определить непосредственно направление реакции нельзя, за исключением тех частных случаев, которые описаны ниже.
Шарнирное соединение препятствует поступательному перемещению тела во всех направлениях в плоскости, перпендикулярной к оси шарнира. Направление реакции неподвижного шарнира может быть любым в зависимости от направления действия остальных сил. Потому сначала определяют две взаимно перпендикулярные составляющие 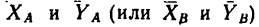
Направление реакции неподвижного шарнира непосредственно определяют в двух следующих случаях:
- а) если, кроме реакции шарнира, все остальные силы (нагрузки и реакция другой связи) образуют систему параллельных сил, то реакция неподвижного шарнира также параллельна всем силам;
- б) если, кроме реакции шарнира, на тело действуют еще только две непараллельные силы, то линия действия реакции неподвижного шарнира проходит через ось шарнира и точку пересечения двух других сил (задачи 47-9 и 48-9).
5. Движение тела может быть ограничено жесткой заделкой в какой-либо опоре (рис. 99). В этом случае даже одна жесткая заделка обеспечивает равновесие тела при любых нагрузках.
ее реакции заранее определить нельзя и сначала определяют составляющие 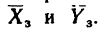
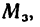
Таким образом, если опорой тела является жесткая заделка, то со стороны последней на тело действуют реакция заделки, которую можно заменить двумя взаимно перпендикулярными составляющими, и момент заделки.
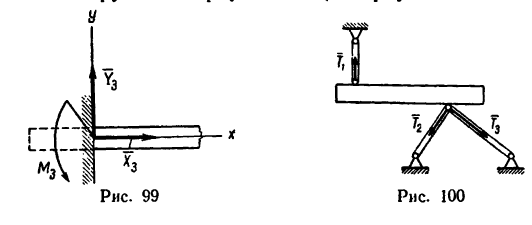
6. Иногда тело удерживается в равновесии при помощи жестких стержней, шарнирно соединенных с телом и с опорами (рис. 100). В отличие от гибкой связи (см. п. 2) такие стержни могут испытывать не только растяжение, но и сжатие.
Возможны и такие случаи, когда нельзя заранее установить, какие стержни растянуты, а какие сжаты. Поэтому при составлении уравнений равновесия исходят из того, что все стержни растянуты. Если же некоторые стержни окажутся в действительности сжатыми, то в результате решения числовые значения реакций таких стержней получатся отрицательными.
Задача 10.
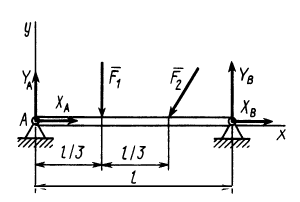
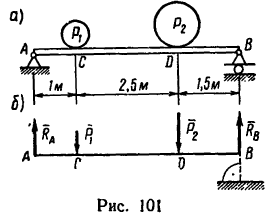
На горизонтальную балку АВ, левый конец которой имеет шарнирно-неподвижную опору, а правый —шарнирноподвижную, в точках С и D поставлены два груза: 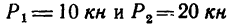
1. Рассмотрим равновесие балки АВ, на которую в точках С и D действуют две вертикальные нагрузки 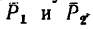
2. Освободив правый конец балки от связи и заменив ее действие реакцией 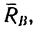
3. Составим систему уравнений равновесия вида (5), приняв для одного уравнения за центр моментов точку А, а для другого — точку В;
4. Решая уравнения, из (I) находим
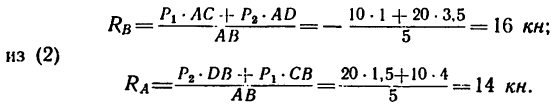
5. Проверим правильность решения, составив уравнение проекций сил на вертикальную ось у:
Подставляя в это уравнение числовые значения, получаем тождество
14 — 10 — 20+16=0 или 0 =0
Значит задача решена правильно.
При решении задач рекомендуется не пренебрегать проверкой. От правильности определения реакций опор зависит правильность всего остального решения или расчета.
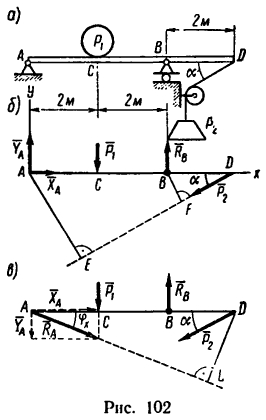
Задача 11.
На консольную балку, имеющую в точке А шарнирно-неподвижную, а в точке В шарнирно-подвижную опору, действуют две сосредоточенные нагрузки: 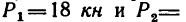
1. Рассматривая находящуюся в равновесии балку AD, видим, что в точке С на нее действует вертикально вниз нагрузка 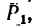
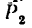
2. Освобождаем балку от связен и заменим их действие реакциями. В месте шарнирно-подвижной опоры В возникает вертикальная реакция 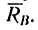
3. Для полученной системы из пяти сил, произвольно расположенных в плоскости, составим систему уравнений равновесия вида (3), расположив ось х вдоль балки, а за центры моментов приняв точки А и В:
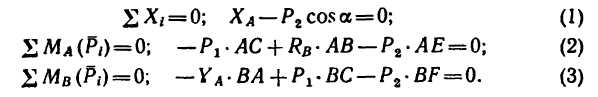
4. Решаем полученные уравнения.
ХА = Р2 cos а = 50 cos 40° = 38,3 кн.
Так как
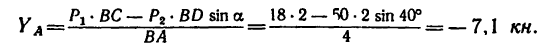
Знак минус, получившийся в последнем случае, показывает, что 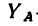
5. При необходимости реакцию 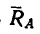
Модуль реакции шарнира А найдем из формулы
Направление реакции Ra установим, определив угол
откуда
6. Проверим правильность решения задачи. Так как при решении не использовано уравнение проекций на ось у, то используем его для проверки:
Уравнение составлено по рис. 102, б.
После подстановки в это уравнение известных значений получим:
В данном случае, проверка решения при помощи уравнения проекций не дает возможности установить правильность определения полной реакции 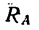
Подставляем в это уравнение числовые значения, имея в виду, что
Расхождение в результатах, равное 0,3, получается из-за округлений при вычислениях.
В следующих задачах проверка решения не приводится и ее рекомендуется производить самостоятельно.
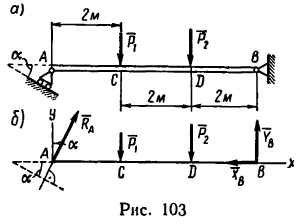
Задача 12.
Горизонтальная балка имеет в точке А шарнирноподвижную опору, плоскость которой наклонена к горизонту под углом а=25° (рис. 103, а), а в точке В — шарнирно-неподвижную опору. Балка нагружена в точках С и D двумя сосредоточенными силами 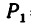
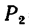
Определить реакции опор.
1. Так же как и в задаче 75-14, балка нагружена двумя параллельными силами, но в отличие от этой задачи здесь реакция подвижного шарнира 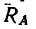
2. Расположив оси х и у как показано на рис. 103, б, составляем уравнения равновесия вида (1):
3. Решаем полученные уравнения. Из уравнения (3) находим 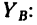
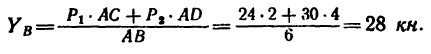
Из уравнения (2) находим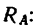
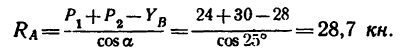
Из уравнения (1) находим
Таким образом, реакция шарнира А
а составляющие реакции шарнира В
и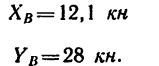
4. Проверку решения производим при помощи уравнения моментов относительно точки С или D.
Следующую задачу рекомендуется решить самостоятельно.
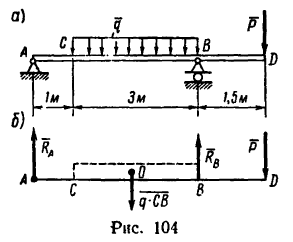
Задача 13.
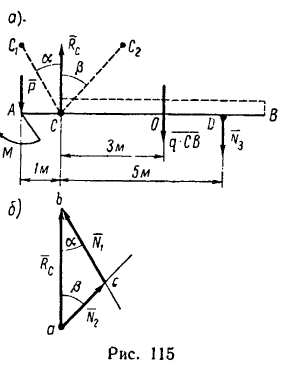
На консольную балку, имеющую в точке А шарнирно-неподвижную, а в точке В шарнирно-подвижную опору,
действуют две нагрузки (рис. 104, а): в точке D — сосредоточенная нагрузка Р=8 кн, а на участке СВ — равномерно распределенная нагрузка интенсивностью q — 2 кн/м. Определить реакции опор.
1. В этой задаче, кроме сосредоточенной силы Р, на участке СВ действует равномерно распределенная сила, интенсивность которой q. Полная величина этой нагрузки (ее равнодействующая) равна q-CB и приложена в точке О посредине участка СВ (рис. 104, б), т. е.
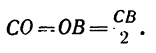
2. Так же как в задаче 75-14, реакция 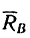
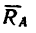
3. Составим два уравнения моментов относительно точек В и А:
4. Из уравнения (1)
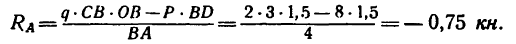
Отрицательное значение реакции 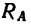
Из уравнения (2) находим
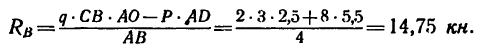
Таким образом, реакция шарнира А равна 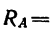
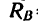
5. Для проверки решения можно использовать уравнение проекций на вертикальную ось.
Задача 14.
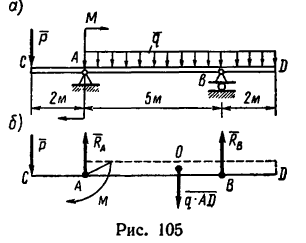
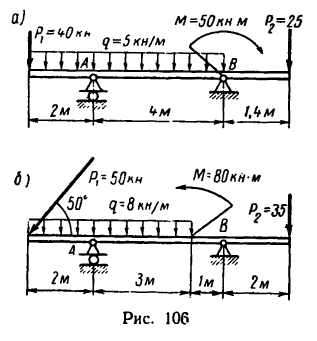
На двухконсольную балку с шарнирно-неподвижной опорой в точке Лис шарнирно-подвижной в точке В действуют, как показано на рис. 105,а, сосредоточенная сила Р—10 кн, сосредоточенный момент (пара сил)
М = 40 кн м и равномерно распределенная нагрузка интенсивностью q — 0,8 кн/м. Определить реакции опор.
1. В отличие от предыдущей задачи здесь, кроме сосредоточенной силы и равномерно распределенной нагрузки, равнодействующая 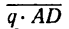
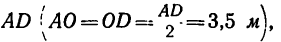
момент М, направленный по часовой стрелке (рис. 105, б).
2. После освобождения балки от связей и замены связей их реакциями 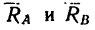
* Перед тем как приступить к рассмотрению этой и следующих задач, необходимо вспомнить два важных свойства нары сил.
3. Составим два уравнения моментов относительно точек В и А:
4. Решая эти уравнения, находим, что
Следующую задачу рекомендуется решить самостоятельно.
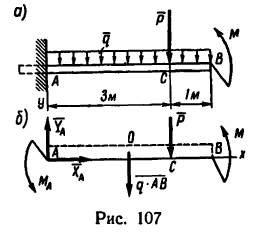
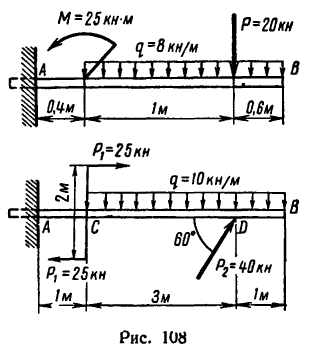
Задача 15.
Жестко заделанная у левого конца консольная балка АВ (рис. 107, а) нагружена равномерно распределенной
нагрузкой интенсивностью q 
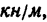
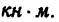
Решение.
1. На балку действуют три нагрузки: в точке С—вертикальная сосредоточенная сила Р, по всей длине балки — равномерно распределенная нагрузка, которую заменим сосредоточенной силой
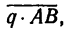
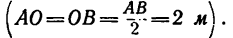
конец балки нагружен моментом М, действующим против хода часовой стрелки (рис. 107, б).
2. Равновесие балки обеспечивается жесткой заделкой у точки А. Освободив балку от связи, заменим ее действие силой — реакцией связи 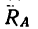
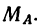
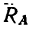
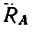
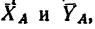
3. Составим уравнения равновесия —уравнение проекции на оси х и у и уравнение моментов относительно точки А:
4. Из уравнения (1)
а это означает, что горизонтальная составляющая реакции заделки 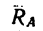
Выше найдено, что 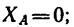
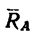
5. Проверку правильности решения можно произвести при помощи уравнения моментов относительно точки С или В. В любое из них входят обе найденные величины.
Следующую задачу рекомендуется решить самостоятельно.
Задача 16.
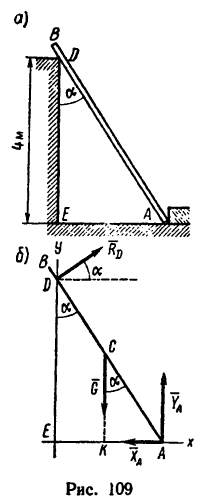
Однородный брус длиной AB = 5 м и весом G = 400 н концом А упирается в гладкий горизонтальный пол и в гладкий вертикальный выступ, а в точке D— в ребро вертикальной стенки высотой ED=4 м. В этом положении брус образует с вертикальной плоскостью стенки угол a = 35° (рис. 109, а). Определить реакции опор.
1. В отличие от предыдущих задач здесь нет ни шарнирных опор, ни жесткой заделки. Брус свободно опирается о пол, выступ и ребро стенки. Нагрузкой является только вес бруса, приложенный по его середине, так как брус однороден.
2. Освободив брус от связей, изобразим его вместе со всеми действующими на него силами (рис. 109, б): в точке С на брус действует
его вес 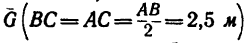
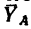
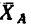
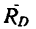
3. Таким образом, на брус действуют четыре силы: 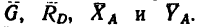
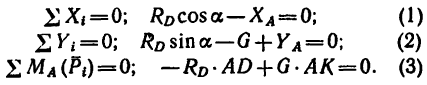
4. Решаем полученную систему уравнений.
Предварительно определяем АК и AD. Из рис. 109, б находим, что
И теперь из уравнения (3):
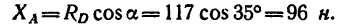
5. Проверку можно произвести при помощи уравнения моментов относительно точки С.
Задача 17.
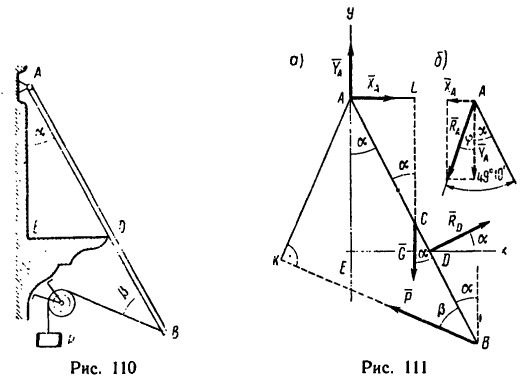
Однородный брус АВ длиной 5 л и весом G = 180 и, прикрепленный к вертикальной стене шарниром А, опирается в точке D на выступ, ширина которого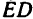
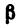
1. К брусу АВ приложены две нагрузки—его собственный вес G в середине бруса (так как брус однородный), действующий вертикальную вниз, и к нижнему концу —сила 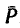
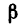
2. Брус, имеет две опоры. В точке D он свободно опирается на ребро выступа ED, и поэтому реакция выступа 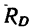
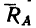
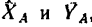
Таким образом, на брус АВ действует уравновешенная система пяти сил
3. Поместив начало осей координат в точке Е и расположив их в соответствии с выбранным направлением сил 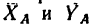
4. Находим плечи AL, AD и АК
Теперь решаем полученные уравнения.
Из уравнения (3)
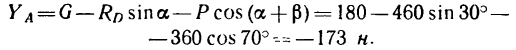
5. Знаки «минус» у числовых значений составляющих реакции шарнира А показывают, что составляющая 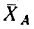
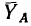
6. Находим модуль полной реакции 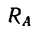
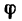
Из рис. 111,6 видно, что реакция шарнира А образует с брусом АВ угол (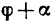
Таким образом, реакция выступа перпендикулярна к брусу и равна 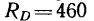
Так как направление и числовое значение полной реакции шарнирно-неподвижной опоры не зависят от первоначально предполагаемого выбора направления составляющих 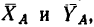
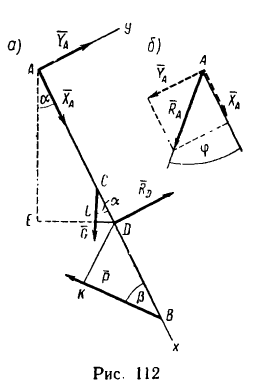
1. Можно, например, предположить, что одна из составляющих реакции шарнира направлена вдоль бруса АВ, а вторая — перпендикулярно к нему.
2. Изобразим при таком предположении силы, приложенные к брусу, на рис. 112, а. Расположим оси х и у как показано на том же рисунке и составим уравнения равновесия, приняв за центр моментов [для уравнения 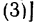
Теперь решим уравнения.
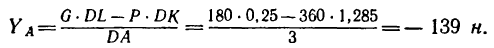
Из уравнения (2)
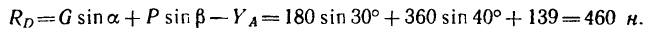
4. Как видно, реакция 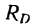
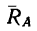
Как видно, результаты получаются те же; небольшое расхождение (0,7%) в значении угла, определяющем направление реакции 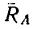
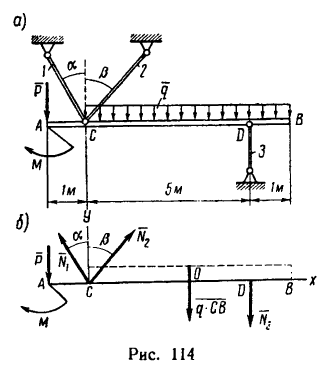
Задача 18.
Балка АВ, нагруженная как показано на рис. 114, а, удерживается в равновесии стержнями 1, 2 и 3, имеющими по
концам шарнирные крепления. Определить реакции стержней.
При этом
1. На балку АВ действуют три нагрузки: в точке А— сосредоточенная сила 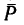
распределенная нагрузка интенсивностью 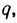
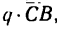
2. Так как прямолинейные стержни при шарнирных креплениях могут только растягиваться или сжиматься, то реакции стержней направлены вдоль них. Предположим, что все стержни растянуты. Заменим их (см. рис. 114,6) реакциями
3. Составим, как обычно, три уравнения равновесия:
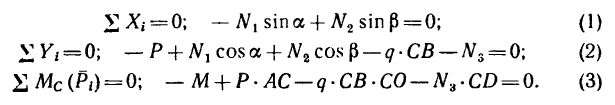
4. Из уравнения (3)
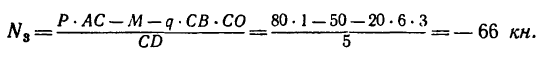
Знак «минус» указывает, на то, что стержень 3 сжат и реакция направлена вверх.
Из уравнения (1) выразим 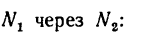
Подставим полученное значение 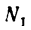
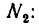
Таким образом, стержни 1 и 2 растянуты и их реакции 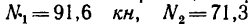
Рассмотренное решение неудобно тем, что оно требует подстановки в одно из уравнений неизвестного из другого уравнения.
Если из числа трех опорных стержней два имеют общий шарнир, то задачу можно решить иначе. Сначала определить реакцию общего шарнира, а затем, используя правило треугольника, найти реакции сходящихся у шарнира стержней.
В рассмотренной задаче обе нагрузки действуют вертикально, а момент только стремится повернуть балку; значит нет усилий, смещающих балку в горизонтальном направлении. Поэтому аналогично тому, как указывалось в задачах 4, нагрузки могут быть уравновешены двумя реакциями, перпендикулярными к балке. А так как реакция стержня 3 перпендикулярна к балке, то и равнодействующая реакций 1 и 2 перпендикулярна к ней. На этом и основывается следующее решение.
1. В отличие от первого решения реакции стержней 1 и 2 заменим их равнодействующей 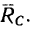
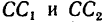
2. Составим два уравнения моментов, приняв за центры моментов точки С и D:
3. Уравнение (1) аналогично уравнению (3) в первом решении. Решая уравнение (1), найдем, что
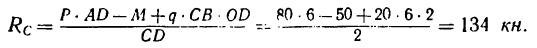
Таким образом, вертикальная равнодействующая реакций 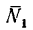
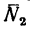
4. Применив правило треугольника, разложим силу 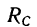
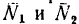
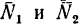
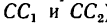
На векторе 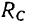
5. На основе теоремы синусов
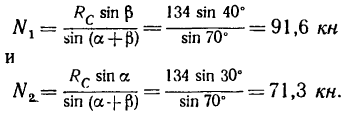
Следующую задачу рекомендуется решить самостоятельно.
Видео:Статика. Формула Пуансо. Лекция (24)Скачать

Справочный материал по статике
В статике изучается равновесие тел под действием сил и свойства систем сил, необязательно находящихся в равновесии.
Задачи статики можно условно разделить на три типа: задачи на равновесие системы сходящихся сил, т.е. сил, линии действия которых пересекаются в одной точке, задачи произвольной плоской системы сил и задачи пространственной системы сил.
Нахождение координат центра тяжести тоже считается задачей статики. Хотя силы в этой задаче явно не присутствуют, основные формулы задачи следуют из уравнений равновесия системы параллельных сил.
Искомыми величинами в задачах статики могут быть реакции опор, усилия в элементах конструкций, геометрические (размеры, углы) и материальные (вес, коэффициент трения) характеристики систем. В статически определимых задачах число уравнений равновесия совпадает с числом неизвестных. Именно такие задачи и будут рассмотрены в этой части.
Для решения задач статики потребуются понятия проекции силы на ось и момента силы относительно точки и оси. Напомним, что проекция вектора силы 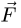
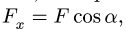
Общее определение момента 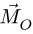
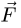
где 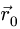
где 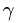
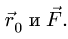
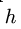
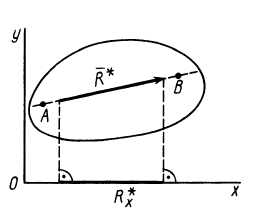
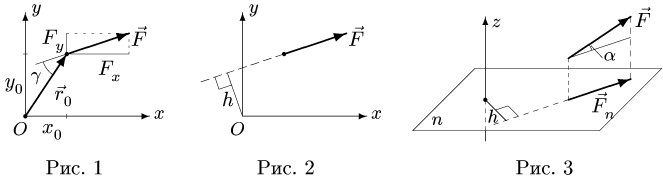
Вектор момента перпендикулярен плоскости, в которой располагаются силы. Поэтому в задачах статики плоской системы сил момент можно рассматривать как скалярную величину — величину проекции вектора момента на нормаль к плоскости (ось 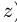
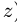
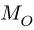
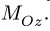
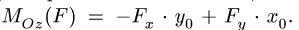
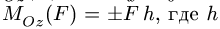
Знак определяется по правилу векторного произведения. Если сила поворачивает тело относительно центра по часовой стрелке — момент отрицательный, против часовой стрелки — положительный. На рис. 2 момент силы 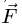
При решении задач пространственной статики (§ 4.3 — § 4.6) требуется вычислять момент силы относительно оси, или, что то же, проекцию момента силы относительно точки (1) на ось, проходящую через нее. Иногда эту величину удобнее искать как момент проекции 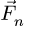
Момент силы относительно оси равен нулю, если сила параллельна оси или пересекает ее, т.е., если сила и ось лежат в одной плоскости.
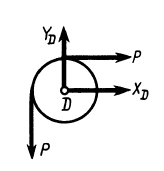
Кроме сил в статике рассматриваются и пары сил. Пара — .это совокупность двух равных параллельных противоположно направленных сил. Пара характеризуется моментом — суммой моментов ее сил относительно некоторой точки. Легко показать, что положение точки не существенно и на величину момента не влияет, поэтому момент пары является свободным вектором. Напомним, что вектор силы является вектором скользящим. В зависимости от знака момента пары на плоскости изображать пару будем изогнутой стрелкой 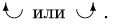
Решение двух задач статики в системе Maple V приведено в § 15.1, 15.2. Большинство задач статики сводится к решению систем линейных уравнений. Рутинную часть работы по составлению и решению уравнений можно поручить Maple V. Простейшая программа может выглядеть, например, так:
Записывая уравнение на компьютере, а не на бумаге, вы достигаете сразу же нескольких целей. Во-первых, компьютер выполняет математические действия, часто весьма громоздкие. Во-вторых, уравнение легко поправить и сразу же пересчитать, если вы ошиблись при составлении уравнения и ответ не сходится. В-третьих, решение удобно оформить, распечатав его на принтере. Можно вывести график, таблицу результатов и т.д. Все эти действия можно выполнить и в других системах, в частности, в пакете AcademiaXXI.
Плоская система сходящихся сил
При изучении темы ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ вы научитесь составлять уравнения проекций и решать задачи равновесия плоских стержневых систем методом вырезания узлов. Этот метод лежит в основе компьютерной программы расчета ферм (§15.1).
Простая стержневая система
Постановка задачи. Плоская шарнирно-стержневая конструкция закреплена на неподвижном основании и нагружена в шарнирах силами. Найти усилия в стержнях.
Рассматриваем равновесие внутренних шарниров системы, не соединенных с неподвижным основанием. Такие шарниры будем называть узлами. Действие каждого стержня заменяем его реакцией — силой, направленной из узла к стержню. Усилие — это проекция реакции стержня на внешнюю нормаль к сечению. Если в результате решения задачи реакция стержня, приложенная таким образом к узлу, оказывается отрицательной, то стержень сжат, в противном случае стержень растянут.
- 1. Вырезаем узел, соединенный только с двумя стержнями. Действие стержней заменяем их реакциями.
- 2. Для полученной системы сходящихся сил составляем уравнения равновесия в проекциях на выбранные для этого узла оси.
- 3. Решаем систему двух линейных уравнений и находим искомые усилия.
- 4. Вырезаем очередной узел системы, тот, к которому подходят не более двух стержней с неизвестными усилиями. Составляем и решаем уравнения равновесия в проекциях на оси, выбранные для этого
Простая стержневая система:
узла. Этот пункт плана выполняем несколько раз для всех узлов до нахождения всех усилий.
- 5. Для проверки решения мысленно отделяем конструкцию от основания, заменяя действие рассеченных стержней найденными реакциями. Проверяем выполнение условий равновесия полученной системы сил.
Замечание 1. Существуют фермы , у которых к каждому узлу присоединены более двух стержней. Например, на рис. 4 изображена конструкция (сетчатая ферма В.Г.Шухова), к каждому узлу которой подходит по три стержня. Диагональные стержни расположены в разных плоскостях и не пересекаются.
Здесь нельзя определять усилия по предложенной схеме, переходя от одного узла к другому, так как нет узла, с которого можно начать расчет. В этом случае сначала составляются уравнения равновесия отдельных узлов, а потом совместно решается система полученных уравнений. Систему можно решать любым известным способом.
Замечании 2. Для упрощения уравнений равновесия одну из осей координат можно направить вдоль стержня с неизвестным усилием. Для каждого узла можно выбрать свою систему координат.
Замечание 3. Углы между осями и векторами усилий легче определять, если проводить через узлы вспомогательные вертикальные или горизонтальные прямые.
Замечание 4. Усилия в стержнях можно найти с помощью системы Maple V (Программа 1, с. 3-50).
*)Шарнирно-стержневая конструкция, нагруженная в шарнирах силами, называется фермой. Весом стержней фермы и трением в шарнирах пренебрегают.
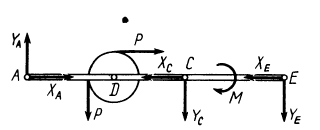
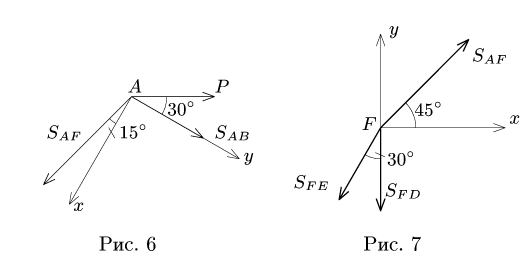
Пример. Плоская шарнирно-стержневая конструкция закреплена на неподвижном основании шарнирами Е, D, С и нагружена в шарнире А горизонтальной силой Р = 100 кН (рис. 5). Даны утлы: 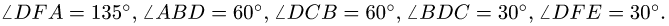
Конструкция состоит из шести стержней, соединенных тремя шарнирами (узлами). Узлы фермы находятся в равновесии. Для каждого узла А, В, F составляем по два уравнения равновесия в проекциях на выбранные оси. Из шести уравнений находим шесть искомых усилий.
1. Решение задачи начинаем с рассмотрения узла А, так как этот узел соединен только с двумя стержнями А В и AF. При вырезании узла действие каждого стержня заменяем силой, направленной из шарнира к стержню (рис. 6).
2. Составляем уравнения равновесия. Для упрощения уравнений ось 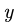
где 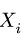
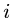
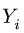
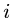
3.Решаем уравнения. Из первого уравнения системы находим усилие 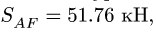
4. Рассматриваем узел F. К нему подходят три стержня (рис. 7).
Усилие в одном из них уже известно 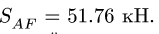
Находим
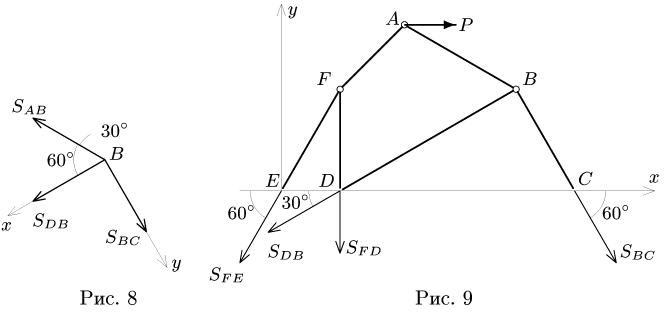
Составляем уравнения равновесия узла В в проекциях на оси, направленные по стержням ВС и BD (рис. 8):
Решая уравнения, получаем:
5. Проверка. Рассматриваем равновесие конструкции в целом.
Горизонтальным сечением отсекаем ферму от основания. Действия стержней заменяем силами, которые направляем, как и раньше, по внешним нормалям к сечениям стержней, т.е. вниз (рис. 9).
Система сил, действующих на ферму, не является сходящейся. Для такой системы справедливы три уравнения равновесия, одно из которых — уравнение моментов. Составление уравнения моментов — тема задач статики произвольной плоской или пространственной системы сил (§2.1 — 3.2). Для того, чтобы не выходить за пределы темы поставленной задачи, в решении которой используются только уравнения проекций, составим два уравнения проекций на оси 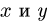
Суммы равны нулю. Это подтверждает правильность решения. Результаты расчетов в кН заносим в таблицу
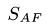 | 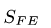 | 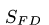 | 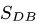 | 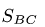 | |
| 51.76 | -73.21 | 73.21 | -26.79 | 36.60 | -63.40 |
Равновесие цепи
Постановка задачи. Определить положение равновесия плоского шарнирно-стержневого механизма, состоящего из последовательно соединенных невесомых стержней. Механизм расположен в вертикальной плоскости. В крайних точках механизм шарнирно закреплен на неподвижном основании. Средние шарниры нагружены силами. Найти усилия в стержнях.
Особенностью задачи является необычный для статики объект исследования — механизм, имеющий возможность двигаться. При определенном соотношении нагрузок и геометрических параметров механизм принимает положение равновесия. В качестве искомой величины может быть угол или какая-либо другая геометрическая характеристика конструкции. План решения
- 1. Записываем уравнения равновесия узлов системы в проекциях.
- 2. Решаем полученную систему уравнений. Определяем усилия в стержнях и искомый угол.
- 3. Проверяем равновесие конструкции в целом, освобождая ее от внешних связей. Проверочным уравнением может быть уравнение проекций на какую-либо ось.
Задача 19.
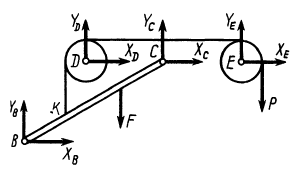
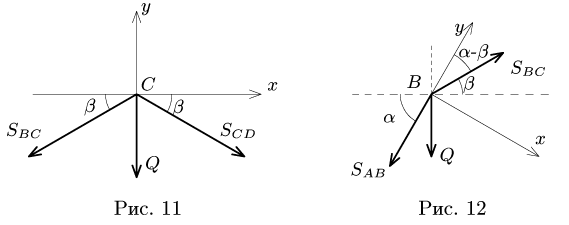
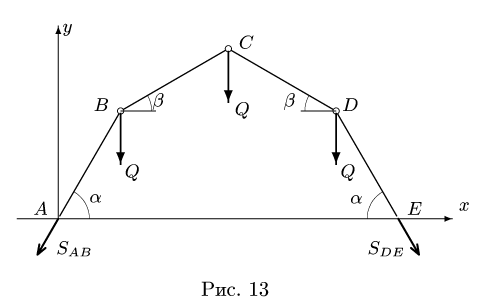
Определить положение равновесия плоского симметричного шарнирно-стержневого механизма. Концы А и Е шарнирно закреплены на неподвижном основании. Три внутренних шарнира В, С и D нагружены одинаковой вертикальной нагрузкой Q.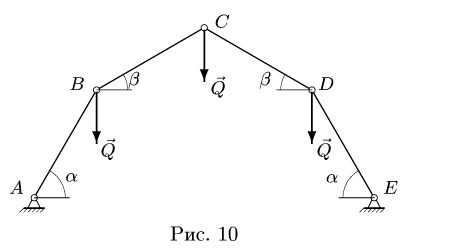
В положении равновесия 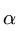
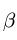
Конструкция, данная в условии задачи, представляет собой механизм, находящийся в равновесии только при некоторых определенных нагрузках. При изменении направлений и величин нагрузок меняется и конфигурация конструкции. Одной из неизвестных величин задачи (помимо усилий в стержнях) является угол 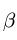
1. Записываем уравнения равновесия узлов системы. Составим уравнения равновесия узла С (рис.11):
Конструкция симметрична, поэтому уравнения равновесия узлов В и D запишутся одинаково. Рассмотрим равновесие узла В (рис.12).
Для упрощения уравнений направим ось у по стержню АВ, ось х — перпендикулярно АВ. Тогда, уравнение равновесия в проекции на ось х содержит только одну неизвестную величину:
2. Решаем систему уравнений (1-4). Из (1) получаем, что 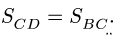
Выражаем 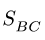
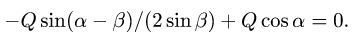
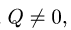
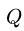
или 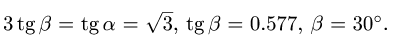
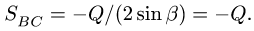
В силу симметрии задачи 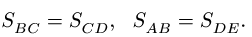
3. Проверка. Рассмотрим равновесие всей конструкции в целом
Отсекая стержни от основания, заменим их действие реакциями, направленными по внешним нормалям к сечениям стержней, т.е. вниз (рис. 13). Уравнение проекций на ось х составлять не имеет смысла — в силу симметрии оно лишь подтвердит, что 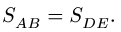
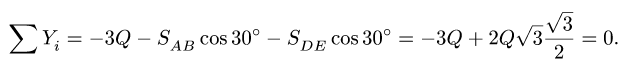
Теорема о трех силах
Постановка задачи. Тело находится в равновесии под действием трех сил, одна из которых известна, у другой известно только направление, а у третьей не известны ни величина, ни направление. Используя теорему о трех силах, найти неизвестные силы.
В теореме о трех силах утверждается, что если на тело, находящееся в равновесии, действуют три непараллельные силы (включая реакции опор), то они лежат в одной плоскости, и линии их действия пересекаются в одной точке.
- 1. Найдем точку пересечения линий действия двух сил, направления которых известны. Через эту точку должна пройти и линия действия третьей силы.
- 2. Имея направления векторов трех сил, строим из них силовой треугольник. Начало одного вектора является концом другого. Если тело находится в равновесии, то сумма векторов сил, действующих на него, равна нулю. Следовательно, треугольник сил должен быть замкнут.
- 3. Из условия замкнутости треугольника по направлению заданной силы определяем направление обхода треугольника и, следовательно, направления искомых сил.
- 4. Находим стороны силового треугольника — искомые силы.
Задача 20.
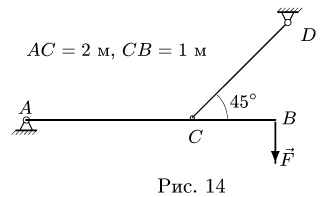
Горизонтальный невесомый стержень А В находится в равновесии под действием трех сил, одна из которых вертикальная сила F = 5 кН (рис. 14), другая — реакция опорного стержня CD, а третья — реакция неподвижного шарнира А. Используя теорему о трех силах, найти неизвестные реакции опор.
1.3. Теорема о трех силах
1. Найдем точку пересечения линий действия двух сил, направления которых известны. Определим направление линии действия третьей силы.
На стержень АВ действуют три силы: заданная сила 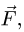
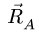
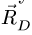
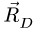
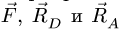
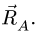
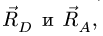
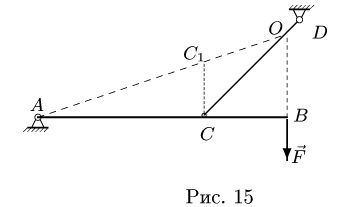
2. Строим силовой треугольник. Сумма векторов сил, находящихся в равновесии, равна нулю, следовательно, треугольник, составленный из 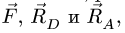
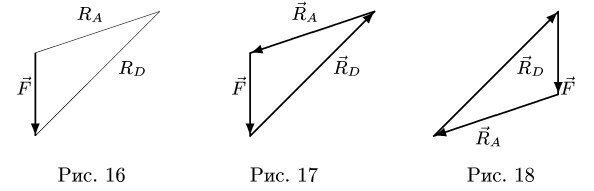
Треугольник строим, начиная с известной силы 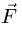
3.Из условия замкнутости треугольника по направлению внешней силы 
Замкнутость треугольника сил означает, что начало одной силы совпадает с концом другой. Отсюда определяем направление обхода треугольника, которое может быть различным в зависимости от способа построения силового треугольника (рис. 17 — против часовой стрелки, рис. 18 — по часовой стрелке). Направления и величины сил в обоих случаях одни и те же.
Изобразим реакции с учетом найденных направлений (рис. 19).
4. Определяем длины сторон силового треугольника — величины реакций опор. Найти стороны треугольника сил означает решить задачу. В нашем случае известны углы (по построению) и сторона F треугольника. Две другие стороны находятся по теореме синусов. 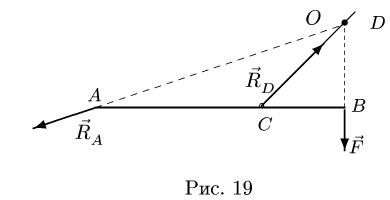
Можно поступить иначе, используя свойства подобия. На рис. 15 найдем треугольник подобный силовому. В ряде случаев этот треугольник очевиден. В общем же, для получения такого треугольника надо выполнить дополнительные построения: провести линии, проходящие через характерные точки (шарниры, точки приложения сил и т.п.), параллельно сторонам силового треугольника. Проведем, например, вертикаль 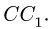
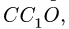
Найдем стороны треугольника
Из подобия 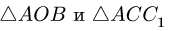
Отсюда вычисляем длины:
1.3. Теорема о трех силах
Из условия подобия треугольника сил и 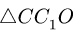
Из этих пропорций находим искомые величины:
Предупреждение типичных ошибок
- Размеры на чертеже сил, приложенных к телу (рис.15), измеряются в единицах длины (м, см), а на силовом треугольнике (рис. 17, 18) в единицах сил
Не надо принимать линейные расстояния АО, СО и ВО за величины соответствующих сил.
- Реакция гладкого основания перпендикулярна поверхности основания. Реакция гладкой поверхности тела о неподвижную опору перпендикулярна поверхности тела.
- В данной задаче должно быть только три силы. Лишние силы возникают, если прикладывать вес тела там, где его нет, или если реакцию в шарнире А раскладывать на составляющие.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Трение
- Пространственная система сил
- Центр тяжести
- Кинематика точки
- Моменты силы относительно точки и оси
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📸 Видео
Момент силыСкачать

Геометрия масс. Теорема о движении центра массСкачать

теорема ШтейнераСкачать

Теоретическая механика термех Статика Нахождение реакции связей часть 2Скачать

5.3. Главный момент произвольной пространственной системы силСкачать

ЗАДАЧА - ЧУДО! Победи мастера, найди угол альфа!Скачать

Статика. Теорема Пуансо. Лекция (20)Скачать

Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Нахождение площади и теорема Вариньона | Ботай со мной #005 | Борис Трушин ||Скачать

Статика. Пара сил. Лекция (17)Скачать

🔺📏 Теорема Вариньона: Новая глава геометрии! 🔺📏Скачать





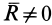 Равнодействующая сила
Равнодействующая сила 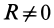 и главный момент
и главный момент 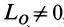 , то такую систему можно упростить и привести к одной равнодействующей силе
, то такую систему можно упростить и привести к одной равнодействующей силе 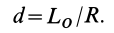
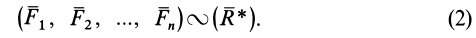
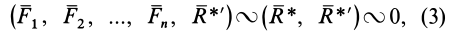
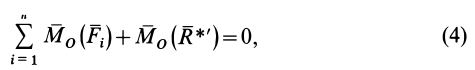
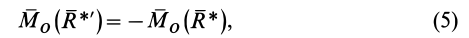
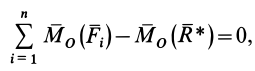
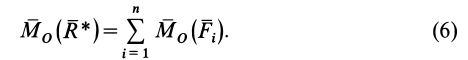
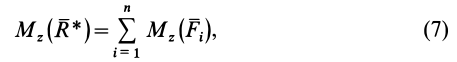
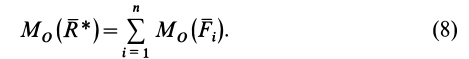
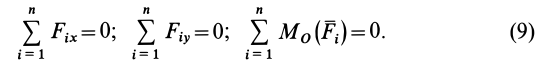
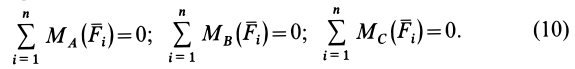
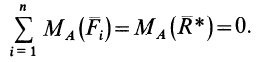
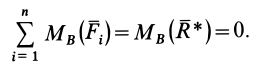
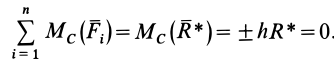
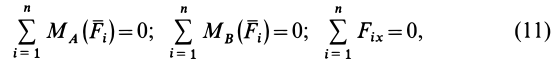
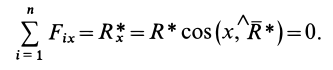
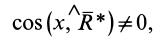
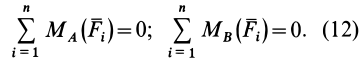
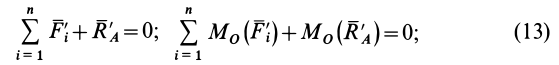
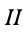
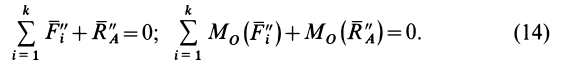

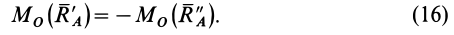
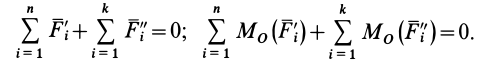
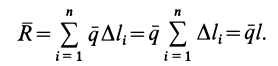
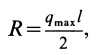
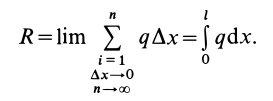
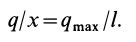
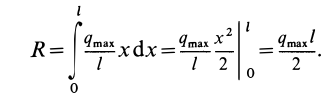
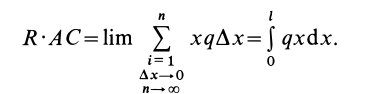
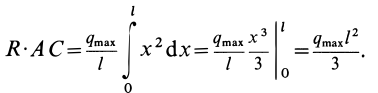
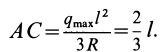
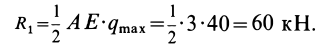
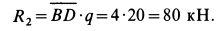
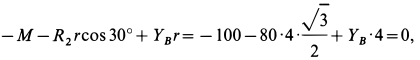
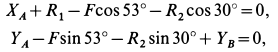
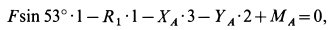
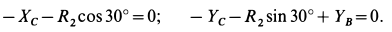
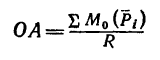
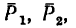
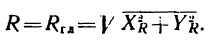
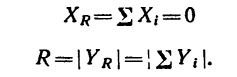
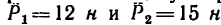
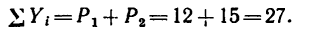
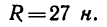
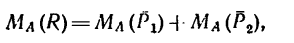
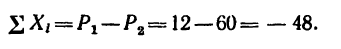
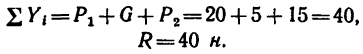
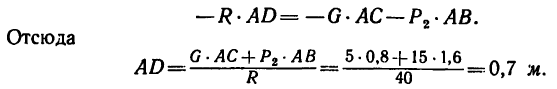
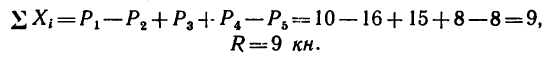
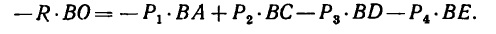
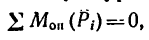
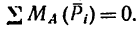
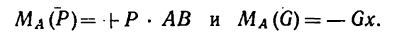
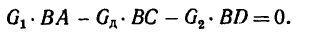
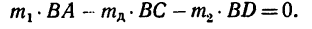
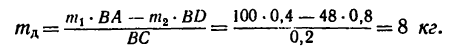
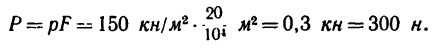
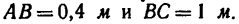
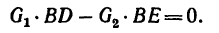
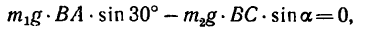
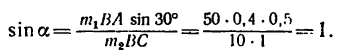
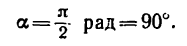

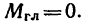



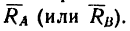
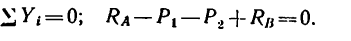
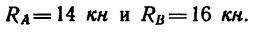
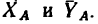
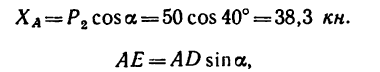
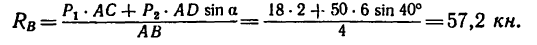
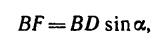
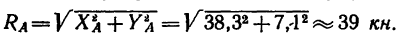
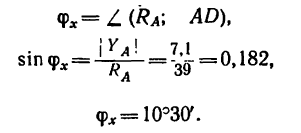
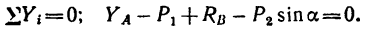
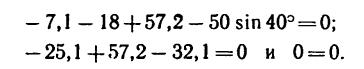
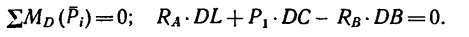
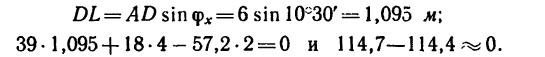
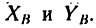
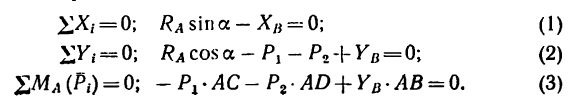
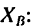
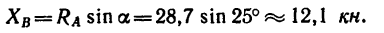
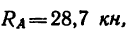
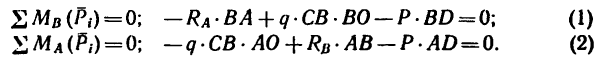
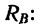
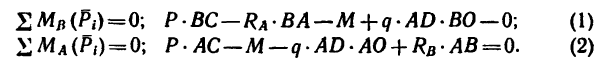
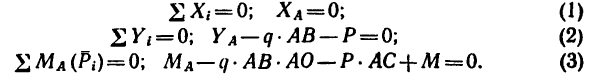
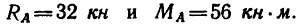
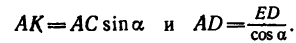
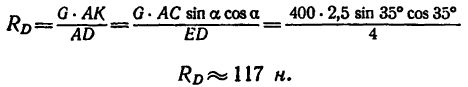
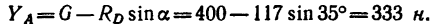
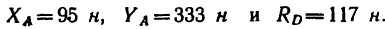
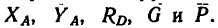
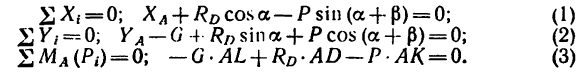
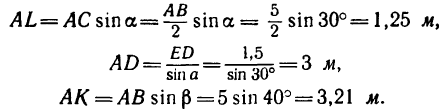
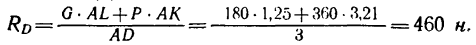
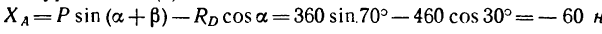
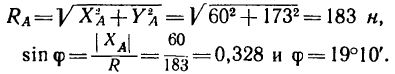
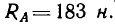
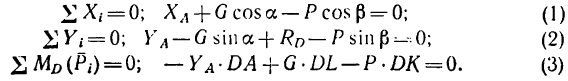
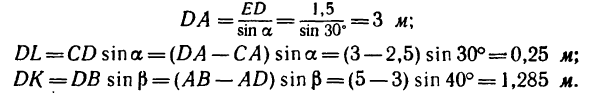
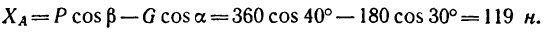
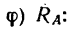
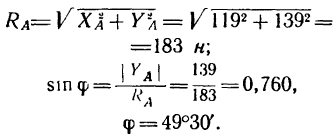
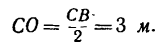
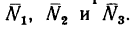
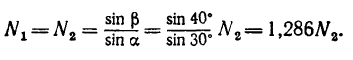
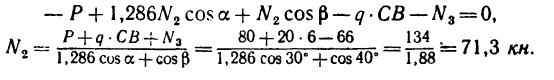
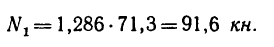
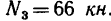
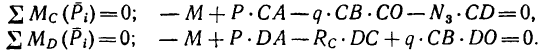
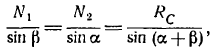
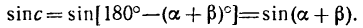

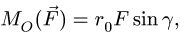
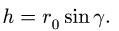

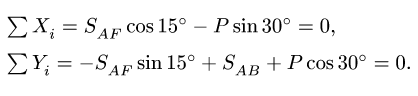
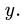
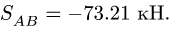
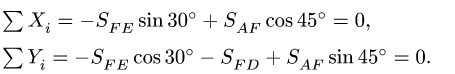
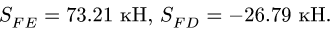
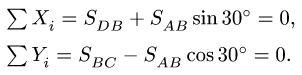
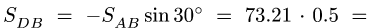
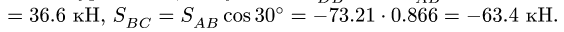
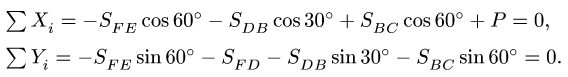
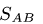
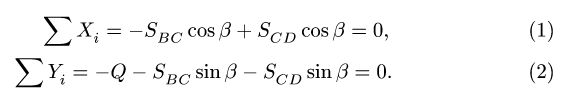
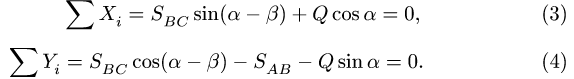
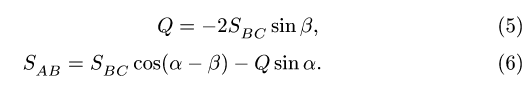
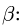

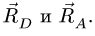
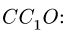
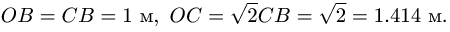
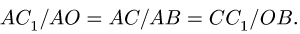
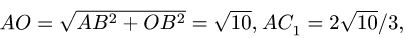
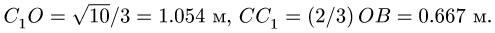
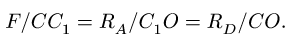
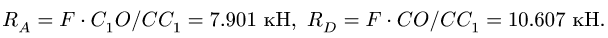
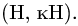 Не надо принимать линейные расстояния АО, СО и ВО за величины соответствующих сил.
Не надо принимать линейные расстояния АО, СО и ВО за величины соответствующих сил.