Главный вектор и главный момент сил инерции теоретическая механика

Находить значения главного вектора и главного момента сил инерции непосредственно по формулам (22.6) затруднительно, так как в общем случае будем иметь дело с множеством сил инерции всех материальных точек системы. Поэтому целесообразно получить выражения главного вектора и главного момента сил инерции через параметры, характеризующие в целом механическую систему и ее движение.

Подставив в первое из равенств (22.7) значение ZT 7 / из теоремы о движении центра масс Ма_с = ЕГ/ (см. § 17.3), найдем

т. е. главный вектор сил инерции механической системы направлен противоположно вектору а_с, а модуль его равен произведению массы системы на ускорение ее центра масс.

Подставив теперь во второе из равенств (22.7) значение ‘Lni₀(F_k e ) из теоремы моментов (см. § 18.2) dK₀/dt = Y.m₀(F?), найдем

т. е. главный момент сил инерции механической системы относительно некоего центра О направлен противоположно вектору производной по времени от кинетического момента системы относительно того же центра.

Аналогичным будет соотношение для моментов относительно оси. Так, относительно оси z будет

Таким образом, все силы инерции механической системы можно эквивалентно заменить двумя векторами: силой Я ф , приложенной в произвольно выбранном центре О, и парой сил с моментом, равным М ф .

Рассмотрим, как эти величины определяются для твердого тела.

Если тело совершает поступательное движение, то ускорения всех его точек одинаковы и равны ускорению а_с центра масс С

тела (а_к =а_с). Следовательно, все силы инерции —т_ка_к образуют систему параллельных сил, которая приводится к равнодействующей Я ф = -Ма_с, линия действия которой будет проходить через точку С (здесь полная аналогия с силами тяжести). Сумма моментов сил инерции относительно точки С будет равна нулю.

Для твердого тела, вращающегося вокруг неподвижной оси Oz, величину главного момента сил инерции относительно этой оси определим, подставив в формулу (22.11) значение K_z = J_zсо (см. § 18.1):

т. е. модуль M°_Z = J_zs, а направление момента противоположно

направлению углового ускорения е (это следует учитывать при выполнении чертежей для расчета).

Следовательно, система сил инерции такого вращающегося тела приводится к приложенной в точке О силе Я ф , определяемой формулой (22.8), и к паре, момент которой определяется формулой (22.12).

В частном случае, когда тело вращается вокруг оси Cz, проходящей через его центр масс С, получим R ф = 0, так как а_с = 0, и система сил инерции приводится лишь к одной паре с моментом

ф , определяемой формулой (22.8) и приложенной в центре масс С тела, и паре сил с моментом = — /_Сге (ось Cz перпендикулярна плоскости движения).

Видео:Момент силы относительно точки и осиСкачать

Теоретическая механика. В помощь студенту

Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.

Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.

Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.

Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.

Видео:§4.3. Главный вектор и главный момент сил инерцииСкачать

Статика твердого тела

Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.

Основные понятия и законы статики

Эквивалентные системы сил – это такие системы сил, замена которых одна на другую не изменяет механического состояния тела.
Принятое обозначение: .

Уравновешенная система сил – это система сил, которая будучи приложена к свободному твердому телу не изменяет его механического состояния (не выводит из равновесия).
.

Равнодействующая сила – это сила, действие которой на тело эквивалентно действию системы сил.
.

Пара сил – это система двух параллельных равных по модулю противоположно направленных сил.
Принятое обозначение: .
Под действием пары сил тело будет совершать вращательное движение.

Закон 4. Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке, равна по модулю диагонали параллелограмма, построенного на этих силах, и направлена вдоль этой
диагонали.
По модулю равнодействующая равна:

Связи и их реакции
• Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности.
• Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры.
• Шарнирная неподвижная опора противодействует любому перемещению в плоскости, перпендикулярной оси вращения.
• Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня.
• Глухая заделка противодействует любому перемещению и вращению в плоскости. Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.

Момент силы относительно точки
• Абсолютное значение момента равно произведению модуля силы на кратчайшее расстояние h от центра вращения до линии действия силы. Расстояние h называют плечом силы.
  
• Момент считают положительным, если сила стремится вращать плечо h против хода часовой стрелки и отрицательным при вращении по ходу часовой стрелки.
• Свойства момента силы относительно точки:
  1) Момент силы не изменится при переносе точки приложения силы вдоль линии действия силы.
  2) Момент силы равен нулю, если линия действия силы проходит через точку приложения силы.
  3) Момент равнодействующей силы относительно точки равен сумме моментов слагаемых сил относительно этой точки.
  ,
  где

Момент силы относительно оси
• Момент силы относительно оси — это момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
  Момент считается положительным, если с положительного конца оси поворот, который сила стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.
  
• Чтобы найти момент силы относительно оси, нужно:
  1) Провести плоскость перпендикулярную оси z.
  2) Спроецировать силу на эту плоскость и вычислить величину проекции .
  3) Провести плечо h из точки пересечения оси с плоскостью на линию действия проекции силы и вычислить его длину.
  4) Найти произведение этого плеча и проекции силы с соответствующим знаком.
• Свойства момента силы относительно оси.
  Момент силы относительно оси равен нулю, если:
  1) , то есть сила параллельна оси.
  2) h=0, то есть линия действия силы пересекает ось.

Момент пары сил
• Момент пары сил равен произведению одной силы на кратчайшее расстояние между линиями действия сил пары, которое называется плечом пары (пара сил оказывает на тело вращающее действие)
  ,
  где: — силы, составляющие пару;
  h — плечо пары.
  Момент пары считают положительным, если силы стремятся вращать плечо против хода часовой стрелки.
• Свойства пары сил.
  1) Сумма проекций сил пары на любую ось равна нулю.
  2) Не изменяя момента пары можно одновременно соответственно изменять значение сил и плечо пары.
  3) Пару можно переносить в плоскости ее действия при этом действие пары на тело не изменится.

Преобразование сходящейся системы сил
• Равнодействующая двух сходящихся сил находится на основании аксиомы о параллелограмме сил.
  Геометрическая сумма любого числа сходящихся сил может быть определена путем последовательного сложения двух сил – способ векторного многоугольника.
  Вывод: система сходящихся сил () приводится к одной равнодействующей силе .
• Аналитически равнодействующая сила может быть определена через ее проекции на оси координат:
  
  Согласно теореме: проекция равнодействующей на ось равна сумме проекций слагаемых сил на эту ось: , или в общем виде
  С учетом равнодействующая определяется выражением:
  .
• Направление вектора равнодействующей определяется косинусами углов между вектором и осями x, y, z:
  

Преобразование произвольной системы сил
• Теорема: силу, приложенную к твердому телу, можно, не изменяя оказываемого ею действия, перенести параллельно в другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы относительно точки, в которую она переносится.
  В результате указанного преобразования получается сходящаяся система сил и сумма моментов пар сил. Действие сходящейся системы сил заменяют действием суммарной силы, действие моментов — суммарным моментом.
  Суммарный вектор — это главный вектор системы сил.
  Суммарный момент — это главный момент системы сил.
  Вывод: произвольная система сил в результате тождественного преобразования приводится к главному вектору и главному моменту системы сил.
• Аналитически главный вектор и главный момент системы сил могут быть определены через их проекции на оси координат:
  ,
  

Условия равновесия систем сил
• Равновесие системы сходящихся сил
  Действие системы сходящихся сил эквивалентно действию одной равнодействующей силы.
  Для равновесия тела необходимо и достаточно, чтобы равнодействующая равнялась нулю .
  Из формулы следует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю:
  
• Для равновесия плоской сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y равнялась нулю:
  

Равновесие произвольной системы сил.
• Действие произвольной системы сил эквивалентно действию главного вектора и главного момента. Для равновесия необходимо и достаточно выполнения условия:
  .
• Для равновесия произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси X,Y,Z и суммы моментов всех сил относительно осей X,Y,Z равнялись нулю:
  
• Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций главного вектора на оси X,Y, и алгебраическая сумма моментов сил относительно центра О были равны нулю:
  

Видео:Момент инерцииСкачать

Кинематика

Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.

Основные понятия кинематики

Способы задания движения точки
• Задать движение точки — значит задать изменение ее положения по отношению к выбранной системе отсчета. Существуют три основные системы отсчета: векторная, координатная, естественная.
• В векторной системе положение точки относительно начала отсчета задается радиус-вектором.
  Закон движения: .
• В системе координат OXYZ положение точки задается тремя координатами X, Y, Z.
  Закон движения: x = x(t), y = y(t); z = z(t).
• В естественной системе отсчета положение точки задается расстоянием S от начала отсчета до этой точки вдоль траектории.
  Закон движения: .
  Движение точки, при естественном способе задания движения, определено если известны:
  1) Траектория движения.
  2) Начало и направление отсчета дуговой координаты.
  3) Уравнение движения.
  При естественном способе задания движения, в отличии от других способов, используются подвижные координатные оси, движущиеся вместе с точкой по траектории. Такими осями являются:
  Касательная (τ) – направлена в сторону возрастания дуговой координаты по касательной к траектории.
  Главная нормаль (n) – направлена в сторону вогнутости кривой.
  Бинормаль (b) – направлена перпендикулярно к осям τ, n.

Определение кинематических характеристик точки
• Траектория точки
  В векторной системе отсчета траектория описывается выражением: .
  В координатной системе отсчета траектория определяется по закону движения точки и описывается выражениями z = f(x,y) — в пространстве, или y = f(x) – в плоскости.
  В естественной системе отсчета траектория задается заранее.
• Определение скорости точки в векторной системе координат
  При задании движения точки в векторной системе координат отношение перемещения к интервалу времени называют средним значением скорости на этом интервале времени: .
  Принимая интервал времени бесконечно малой величиной, получают значение скорости в данный момент времени (мгновенное значение скорости): .
  Вектор средней скорости направлен вдоль вектора в сторону движения точки, вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки.
  Вывод:скорость точки – векторная величина, равная производной от закона движения по времени.
  Свойство производной:производная от какой либо величины по времени определяет скорость изменения этой величины.
• Определение скорости точки в координатной системе отсчета
  Скорости изменения координат точки:
  .
  Модуль полной скорости точки при прямоугольной системе координат будет равен:
  .
  Направление вектора скорости определяется косинусами направляющих углов:
  ,
  где — углы между вектором скорости и осями координат.
• Определение скорости точки в естественной системе отсчета
  Скорость точки в естественной системе отсчета определяется как производная от закона движения точки: .
  Согласно предыдущим выводам вектор скорости направлен по касательной к траектории в сторону движения точки и в осях определяется только одной проекцией .

Ускорение точки
• По определению ускорение характеризует изменение скорости, то есть скорость изменения скорости.
• Ускорения точки в векторной системе отсчета
  На основании свойства производной:
  .
  Вектор скорости может изменяться по модулю и направлению.
  Вектор ускорения направлен по линии приращения вектора скорости, т. е. в сторону искривления траектории.
• Ускорение точки в координатной системе отсчета
  Ускорение изменения координат точки равно производной по времени от скоростей изменения этих координат:
  .
  Полное ускорение в прямоугольной системе координат будет определяться выражением:
  .
  Направляющие косинусы вектора ускорения:
  .
• Ускорение точки в естественной системе отсчета Приращение вектора скорости можно разложить на составляющие, параллельные осям естественной системы координат:
  .
  Разделив левую и правую части равенства на dt, получим:
  ,
  где — тангенциальное ускорение;
  — нормальное ускорение;
  R — радиус кривизны траектории в окрестности точки.

Кинематика твердого тела
• В кинематике твердых тел решаются две основные задачи:
  1) задание движения и определение кинематических характеристик тела в целом;
  2) определение кинематических характеристик точек тела.
• Поступательное движение твердого тела
  Поступательное движение — это движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению.
  Теорема:при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения.
  Вывод:поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки.
• Вращательное движение твердого тела вокруг неподвижной оси
  Вращательное движение твердого тела вокруг неподвижной оси — это движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.
  Положение тела определяется углом поворота . Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)
  Закон вращательного движения тела вокруг неподвижной оси .
  Угловую скорость и угловое ускорение тела определим методом дифференцирования:
  — угловая скорость, рад/с;
  — угловое ускорение, рад/с².
  Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точку М, то точка М будет описывать вокруг точки С окружность радиуса R. За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние .
  Модуль линейной скорости:
  .
  Ускорение точки М при известной траектории определяется по его составляющим :
  ,
  где .
  В итоге, получаем формулы
  тангенциальное ускорение: ;
  нормальное ускорение: .

Плоско-параллельное движение твердого тела
• Плоско-параллельное движение твердого тела — это движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных одной неподвижной плоскости.
  Движение сечения S в своей плоскости можно рассматривать как сложное, состоящее из двух элементарных движений:
  1) поступательного и вращательного;
  2) вращательного относительно подвижного (мгновенного) центра.
• В первом варианте движение сечения может быть задано уравнениями движения одной его точки (полюса) и вращением сечения вокруг полюса.
  В качестве полюса может быть принята любая точка сечения.
  Уравнения движения запишутся в виде:
  .
  Ускорение точки движущейся плоской фигуры складывается из ускорения полюса относительно неподвижной системы отсчета и ускорения за счет вращательного движения вокруг полюса.
  
  
• Во втором варианте движение сечения рассматривается как вращательное вокруг подвижного (мгновенного) центра P.
  В этом случае скорость любой точки В сечения будет определяться по формуле для вращательного движения:
  .
  Угловая скорость вокруг мгновенного центра Р может быть определена если известна скорость какой либо точки сечения, например точки А.
  .
• Положение мгновенного центра вращения может быть определено на основании следующих свойств:
  1) вектор скорости точки перпендикулярен радиусу;
  2) модуль скорости точки пропорционален расстоянию от точки до центра вращения ();
  3) скорость в центре вращения равна нулю.
• Теорема:проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки, равны между собой и одинаково направлены.
  Доказательство: расстояние АВ изменяться не может, следовательно, не может быть больше или меньше .
  Вывод:.

Сложное движение точки
• Относительное движение — это движение точки относительно подвижной системы.
  Переносное движение — это движение точки вместе с подвижной системой.
  Абсолютное движение — это движение точки относительно неподвижной системы.
  Соответственно называют скорости и ускорения:
  — относительные;
  — переносные;
  — абсолютные.
• Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей (согласно теореме о сложении скоростей):
  .
  Абсолютное значение скорости определяется по теореме косинусов:
  .
• Ускорение по правилу параллелограмма определяется только при поступательном переносном движении
  .
  .
• При непоступательном переносном движении появляется третья составляющая ускорения, называемое поворотным или кориолисовым.
  ,
  где .
  Кориолисово ускорение численно равно:
  ,
  где – угол между векторами и .
  Направление вектора кориолисова ускорения удобно определять по правилу Н.Е. Жуковского: вектор спроектировать на плоскость, перпендикулярную оси переносного вращения, проекцию повернуть на 90 градусов в сторону переносного вращения. Полученное направление будет соответствовать направлению кориолисова ускорения.

Видео:Моменты силы, импульса, инерции. Динамика вращательного движенияСкачать

Динамика

Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.

Основные понятия динамики

Центр масс механической системы — геометрическая точка, координаты которой определяются формулами:

где m_k, x_k, y_k, z_k — масса и координаты k-той точки механической системы, m — масса системы.
В однородном поле тяжести положение центра масс совпадает с положением центра тяжести.

Момент инерции материального тела относительно оси – это количественная мера инертности при вращательном движении.
Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси:
.
Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек:

Сила инерции материальной точки — это векторная величина, равная по модулю произведению массы точки на модуль ускорения и направленная противоположно вектору ускорения:

Сила инерции материального тела — это векторная величина, равная по модулю произведению массы тела на модуль ускорения центра масс тела и направленная противоположно вектору ускорения центра масс: ,
где — ускорение центра масс тела.

Элементарный импульс силы — это векторная величина , равная произведению вектора силы на бесконечно малый промежуток времени dt:
.
Полный импульс силы за Δt равен интегралу от элементарных импульсов:
.

Элементарная работа силы — это скалярная величина dA, равная скалярному произведению вектора силы на бесконечно малое перемещение .
Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов:
,
где α — угол между направлениями векторов перемещения и силы.

Работа силы на конечном перемещении точки её приложения равна интегралу от элементарной работы, взятому по перемещению:
.
Единица измерения работы — Джоуль (1 Дж = 1 Н·м).

Количество движения материальной точки — это векторная величина , равная произведению массы m на её скорость :
.

Количество движения механической системы равно векторной сумме количества движения её точек.
или
,
где m — масса механической системы, — вектор скорости центра масс системы.

Кинетическая энергия материальной точки — это скалярная величина Т, равная половине произведения массы точки на квадрат её скорости:
.

Кинетическая энергия механической системы равна сумме кинетических энергий всех её точек:
.

Аксиомы динамики
• Первая аксиома — это закон инерции.
  Если на свободную материальную точку не действуют никакие силы или действует уравновешенная система сил, то точка будет находиться в состоянии покоя или равномерного прямолинейного движения.
• Вторая аксиома — закон пропорциональности ускорения.
  Ускорение, сообщаемое материальной точке действующей на неё силой, пропорционально этой силе и по направлению совпадает с направлением силы: — это основной закон динамики.
• Третья аксиома — это закон противодействия.
  Силы, с которыми действуют друг на друга две материальные точки, равны по модулю и направлены вдоль прямой, соединяющей эти точки, в противоположные стороны:
  .
• Четвертая аксиома — закон независимости действия сил.
  При действии на материальную точку системы сил полное ускорение этой точки равно геометрической сумме ускорений от действия каждой силы:
  

Дифференциальные уравнения динамики
• Дифференциальные уравнения движения точки связывают ускорение точки с действующими на нее силами. Фактически дифференциальные уравнения являются записью основного закона динамики в явной дифференциальной форме.
  Для абсолютного движения точки (движение в инерциальной системе отсчета) дифференциальное уравнение имеет вид:
  .
• Векторное уравнение может быть записано в проекциях на оси прямоугольной инерциальной системы координат:
  
• При известной траектория движения точки уравнение может быть записано в проекциях на оси естественной системы координат:
  
  С учетом того, что ,
  где — тангенциальное ускорение;
  — нормальное ускорение,
  уравнения примут вид:
  

Общие теоремы динамики
• Общие теоремы динамики устанавливают зависимость между мерами механического движения и механического взаимодействия. Выводы теорем являются результатом тождественного преобразования основного закона динамики.
• Теорема об изменении количества движения: изменение количества движения материальной точки (механической системы) за конечный промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени — для материальной точки;
  — для механической системы.
• Теорема об изменении кинетической энергии: изменение кинетической энергии точки (механической системы) при её перемещении равно сумме работ всех действующих внешних сил на этом перемещении — для материальной точки;
  — для механической системы.
• Кинетическая энергия механической системы определяется в соответствии с , при этом для твердых тел выведены следующие зависимости:
  — при поступательном движении тела;
  — при вращательном движении тела;
  — при плоско-параллельном движении тела.
• Момент инерции цилиндра относительно его оси:
  .
• Момент инерции стержня относительно оси z:
  .
• Момент инерции прямоугольной пластины относительно осей х и y: .
• Момент инерции шара определяется по формуле:
  .
• Работа силы тяжести:
  ,
  где P — сила тяжести;
  h — изменение положения тела по вертикали.
• Работа силы при вращательном движении тела
  ,
  где M — момент силы,
  w — угловая скорость тела.
  Следует иметь в виду, что работа, как скалярная величина, может быть положительной или отрицательной. Работа будет положительной если направление действия силы совпадает с направлением движения.

Принцип Даламбера
• Формулировка принципа Даламбера: если в любой момент времени к действующим на точку силам присоединить силы инерции, то полученная система сил будет уравновешенной:
  .
• Для механической системы:
  .

Видео:2.2. Главный вектор и главный момент плоской системы сил. Приведение к простейшему видуСкачать

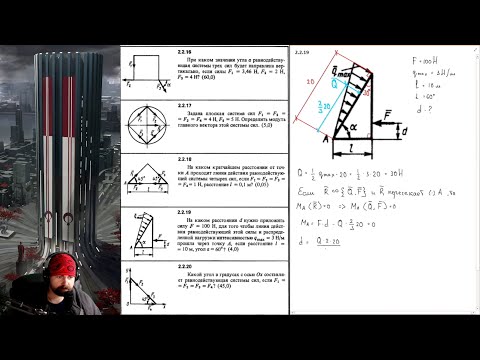
Примеры решения задач

Решение примеров по теме: «Статика твердого тела»

Пример 1. Условия равновесия

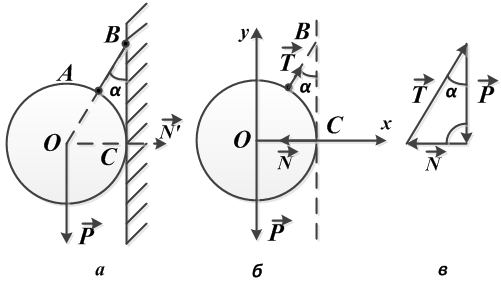
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.

Дано: P = 10 Н; α = 45°
Найти: N, T — ?

Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.

Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).

Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).

При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).

В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:

После подстановки в формулы числовых значений, получим:
.

Ответ: .

Решение примеров по теме: «Кинематика»

Пример 2. Уравнение траектории точки

Дано:
Движение точки задано уравнениями ;
(x, у — в сантиметрах, t — в секундах).
Найти: уравнение траектории точки в координатной форме.

Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:
.

Опуская промежуточные выражения, получаем уравнение траектории:
.

Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).

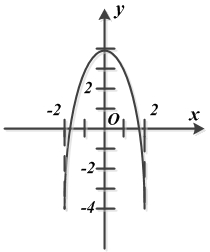
Ответ: .

Решение примеров по теме: «Динамика»

Пример 3. Основной закон динамики точки

Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.

Дано: m = 10 кг; a = 0,5 м/с 2 .
Найти: F — ?

Решение.
Согласно основному закону динамики: .

Подставив значения в формулу, получим:

Ответ: сила, сообщающая массе, равной 10 кг,
ускорение 0,5 м/с 2 , равна 5 Н.

В помощь студенту

Формулы, правила, законы, теоремы, уравнения, примеры решения задач

Список литературы:
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах.
Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие.

Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Главный вектор и главный момент сил инерции

Сравнивая первое из равенств (9.6) с уравнением

,

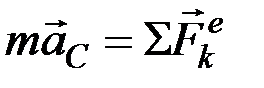
выражающим теорему о движении центра масс (в этой главе массу системы обозначаем буквой ), найдём, что

, (9.7)

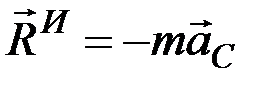
т.е. главный вектор сил инерции механической системы (в частности, твёрдого тела) равен произведению массы системы (тела) на ускорение центра масс и направлен противоположно этому ускорению.

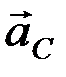
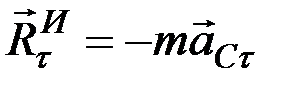
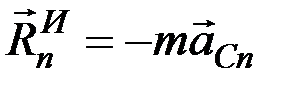
Если ускорение разложить на касательное и нормальное, то вектор разложится на составляющие:

, . (9.8)

Сравнивая теперь второе из равенств (9.8) с уравнением

,

выражающим теорему об изменении главного момента количеств движения системы (кинетического момента), и учитывая, что аналогичным будет соотношение и для моментов относительно оси, получим:

и , (9.9)

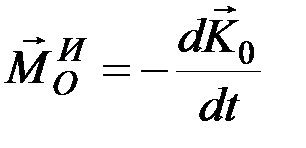
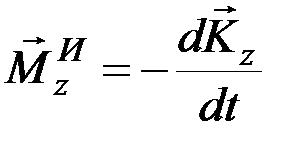
т.е. главный момент сил инерции механической системы (твёрдого тела) относительно некоторого центра О или оси z равен взятой со знаком минус производной по времени от кинетического момента системы (тела) относительно того же центра или той же оси.

📺 Видео

Момент силыСкачать

Момент силыСкачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Теоретическая механика. Задание С6 (часть 9) из сборника ЯблонскогоСкачать

Приведение системы сил к простейшему видуСкачать

СКД Лекция 03 ПОЛНАЯ Момент силы Теория пар силСкачать

Статика. Пара сил. Лекция (17)Скачать

Момент силы относительно точкиСкачать

Урок 80 (осн). Момент силы. Правило моментовСкачать