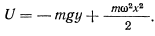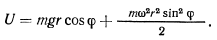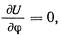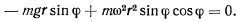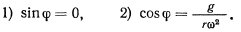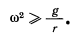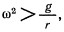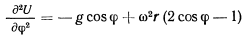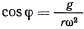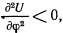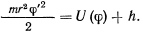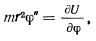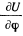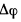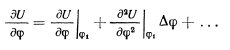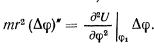Гладкая проволочная окружность радиуса r вращается вокруг вертикального диаметра (8 видео)

Гладкая проволочная окружность радиуса r вращается вокруг вертикального диаметра

2017-03-18
Сфера радиуса $R=0,5 м$ вращается вокруг своего вертикального диаметра с постоянной угловой скоростью $omega = 5 рад/с$ (рис.). Вместе со сферой на ее внутренней поверхности вращается небольшое тело, находящееся на высоте, равной половине радиуса.
1) Определите минимальное значение коэффициента трения, при котором это состояние возможно.
2) Найти минимальное значение коэффициента трения, если угловая скорость сферы равна $omega = 8 рад/с$.
3) Исследуйте устойчивость состояний при найденных значениях коэффициента трения при: а) малых изменениях угловой скорости сферы; б) малых изменениях положения тела.

рис.1

рис.2

рис.3

рис.4

рис.5

рис.6

рис.7

1—2) На рис. 1 показаны силы, действующие на тело: сила тяжести $m vec$, сила реакции со стороны сферы $vec$ и сила трения $vec_$ Сила трения перпендикулярна силе реакции, но направление ее nei известно: она может быть направлена так, как показано на рис.1 или в противоположную сторону.

Равнодействующая $vec_$ этих трех сил

сообщает телу центростремительное ускорение

$a_ = omega^ r = omega^ R sin alpha$,

где $alpha$ — угол между радиусом ОС и вертикалью.

Следовательно, вектор $vec_$ направлен к оси вращения и перпендикулярен ей. Модуль этой силы равен

$F_ = m omega^ R sin alpha$,

В зависимости от направления вектора силы трения $vec_$ модуль силы $F_$ будет иметь разные значения, Это хорошо видно из рис. 2 и 3, (Аналогичный метод исследования был применен нами при решении задачи 2403)

Так как угол между векторами $m vec$ и $vec$ равен $alpha$, получим

$F_ = mg tg (alpha — beta)$, (1)

если сила трения направлена так, как показано иа рис, 2.

Если сила трения направлена в противоположную сторону, то

$F_ = mg tg ( alpha + beta)$, (2)

Это ясно из соотношения

$tg beta = F_/N = mu N/N = mu$.

Следовательно, для равновесия тела на сфере должно выполняться условие

$mu geq tg beta$. (3)

Значение $tg beta$ нетрудно найти из выражений (1) и (2). Учитывая, что

Минимальное значение $mu$ равно

При условии $omega = omega_ = 5 рад/с$ выполняется неравенство

$g > omega^ R cos alpha$, так как $10 > 25 cdot 0,5 cdot cos 60^$,

При условии $omega = omega^ = 8 рад/с$ выполняется неравенство

$g omega_ mu_$ определяется выражением (6).

3) а) При небольшом увеличении угловой скорости $omega$ от значения $omega_ = 5 рад/с$ равнодействующая всех сил $F_ = m omega^ R sin alpha$ также возрастает.

Из рис. 5, а видно, что при этом модуль силы трения $F_^$ уменьшается, а модуль силы $N^$ реакции опоры возрастает. В результате минимальный коэффициент трения $mu_$, необходимый для удержания тела на сфере в положении, характеризуемом углом $alpha$ уменьшается:

$mu_ = | tg beta|$, где $tg beta = F_/N$,

Следовательно, при небольшом увеличении угловой скорости ($omega > omega_$) тело сохранит свое первоначальное положение.

ри небольшом уменьшении угловой скорости ($omega omega_$, кривая 3 — случаю $omega omega_$) минимальный коэффициент трения, необходимый для удержания тела на сфере в положении, характеризуемом углом $alpha = 60^$, уменьшается. А так как тело до изменения угловой скорости имело больший коэффициент трения, то оно сохранит свое первоначальное положение.

При уменьшении угловой скорости ($ omega omega_$) минимальный коэффициент трения, необходимый для удержания тела в положении, характеризуемом углом $alpha_ = 60^$, возрастает (кривая 2) и становится больше имеющегося, поэтому тело не сможет остаться в прежнем положении и поднимется.

При незначительном уменьшении угловой скорости ($omega < omega_$) минимальный коэффициент трения, необходимый для удержания тела в положении, характеризуемом углом $alpha_ = 60^$, уменьшается (кривая 3), поэтому тело сохраняет свое прежнее положение.

Содержание

Окружность радиуса , плоскость которой вертикальна, вращается вокруг своего вертикального неподвижного диаметра
Задача №61.
Движение в поле тяжести. Криволинейное движение.
💡 Видео

Видео:По гладкой проволочной винтовой линии радиусаСкачать

Окружность радиуса , плоскость которой вертикальна, вращается вокруг своего вертикального неподвижного диаметра

Задача №61.

Окружность радиуса , плоскость которой вертикальна, вращается вокруг своего вертикального неподвижного диаметра с постоянной по величине угловой скоростью . По окружности может свободно скользить тяжелая материальная точка массы . Определить положение относительного равновесия материальной точки и найти период малых колебаний точки около положения устойчивого равновесия.

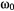
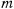
Решение:

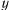
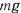
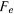
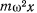
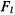
Движение точки определяется относительно вращающейся окружности, поэтому целесообразно подвижную систему отсчета связать с окружностью. Выберем начало подвижной системы координат в центре окружности, ось направим вертикально вверх, а за ось примем горизонтальный диаметр окружности. В этой системе движение точки будет определяться двумя силами: силой тяжести и силой Кориолиса от переносного ускорения, величина которой равна и которая направлена от оси вращения. Сила Кориолиса от добавочного ускорения ортогональна к траектории точки и не влияет на характер движения точки.Сила тяжести и сила Кориолиса допускают существование силовой функции

Если ввести угол 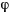, определяющий отклонение точки от вертикального диаметра (начало отсчета в нижней точке), то силовую функцию можно будет записать в виде

В положении равновесия

Отсюда имеем два решения, определяющих положение равновесия точки,

Последнее возможно только тогда, когда

то в нижнем положении

будет величиной положительной, а потому это положение равновесия будет неустойчивым. В положении, где

а потому это положение устойчиво. Для определения периода колебаний точки около положения равновесия обратимся сначала к интегралу живых сил

Дифференцируя это уравнение по времени, получим

в окрестности положения равновесия по малым значениям

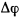
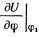
и ограничиваясь малыми членами первого порядка (в положении равновесия — обращается в нуль), будем иметь

Это линейное дифференциальное уравнение в случае, когда

имеет периодическое решение с периодом

Задача взята со страницы подробного решения задач по всем темам теоретической механики:

Возможно эти дополнительные задачи вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Движение в поле тяжести. Криволинейное движение.

Кинематика(6 занятий)

Движение с постоянной скоростью.

Занятие 1

Радиолокатор определяет координаты летящего самолета, измеряя угол между направлением на Северный Полюс и направлением на самолет и расстояние от радиолокатора до самолета. В некоторый момент времени положение самолета определялось координатами α₁= 44°, расстояние R₁= 100 км. Через промежуток времени равный 5 с после этого момента координаты самолета были: α₂= 46°, расстояние R₂ = 100 км. Изобразите в декартовой системе координат с осью у, направленной на север, и с радиолокатором в начале координат положение самолета в оба момента времени; определите модуль и направление его скорости. Угол отсчитывайте по часовой стрелке.

Три микрофона, расположенные на одной прямой в точках А, В, С, последовательно зарегистрировали сигнал в моменты времени t_A>t_B>t_Cзвук от взрыва, который произошел в точке O, лежащей на отрезке АС. Найдите длину отрезка АО, если АВ = ВС = L. В какой момент времени произошел взрыв?

С подводной лодки, погружающейся вертикально и равномерно, испускаются звуковые сигналы длительности t₀. Длительность приема отраженного от дна импульса составляет t. Скорость звука в воде равна с. С какой скоростью погружается подводная лодка?

Из взрывчатого вещества изготовлен стержень длины l. Скорость детонации (скорость вовлечения во взрыв новых участков взрывчатого вещества) равна v, а скорость разлета продуктов взрыва u

Занятие 2

Нарисуйте график зависимости координаты от времени для прямолинейного движения, удовлетворяющего одновременно двум условиям: средняя скорость в промежутке от 2 до 6 с равна 5м/с, максимальная скорость в том же промежутке равна 15 м/с.

Частица, покинув источник, пролетает с постоянной скоростью расстояние L, а затем тормозится с ускорением a. При какой начальной скорости время движения от ее вылета до остановки будет наименьшим?

В коническом сосуде уровень воды поднимается с постоянной скоростью v₀. Как зависит от времени скорость поступления воды в сосуд через трубку сечения s? В нулевой момент времени сосуд пуст.

Задача 11

График зависимости скорости тела от времени имеет вид полуокружности. Максимальная скорость тела равна v₀, время движения t₀. Определите путь, пройденный телом.

Задача 12

Графики зависимости координаты от времени, построенные в различном масштабе времени для двух частиц, оказались одинаковыми. Одно деление оси времени t для графика первой частицы отвечает 4 с, а для графика второй – 1 с. Найдите отношение скоростей и отношение ускорений частиц для точки А графика.

Тело начинает движение из точки А и движется сначала равноускоренно в течение времени t₀, а затем равнозамедленно, с тем же по модулю ускорением. Через какое время от начала движения тело вернется в точку А?

Из одной и той же точки вертикально вверх с интервалом времени ∆tброшены два шарика соскоростью v. Через какое время после вылета второго шарика они столкнутся?

Движение в поле тяжести. Криволинейное движение.

Занятие 3

Из верхней точки окружности по гладкому желобу под углом φ к вертикали начинает скользить шарик. За какое время он достигнет окружности, если ее диаметр равен D?

Под каким углом к вертикали должен быть направлен из точки А гладкий желоб, чтобы шарик соскользнул по нему на наклонную плоскость за наименьшее время?

Из орудия произведен выстрел под углом φ к горизонту. Начальная скорость снаряда v. Поверхность земли горизонтальна. Найдите: горизонтальную и вертикальную компоненты скорости как функцию от времени; зависимость координат х и у от времени; уравнение траектории, т.е. зависимость у от х; время полета, наибольшую высоту и дальность полета снаряда.

С какой скоростью должен в момент старта ракеты вылететь из пушки снаряд, чтобы поразить стартующую вертикально, с ускорением а, ракету? Расстояние от пушки до стартового стола L, пушка стреляет под углом αк горизонту.

Из шланга лежащего на земле под углом α к горизонту бьет струя воды со скоростью v. Определите массу струи находящейся в воздухе, если площадь ее сечения неизменна и равна s.

Занятие 4

Снаряд, вылетев из орудия со скоростью v попал в точку с координатами х и у. Найдите: тангенс угла наклона, образуемого стволом орудия и горизонтом; границу области возможного попадания снаряда; наименьшую потребную скорость снаряда, при которой он сможет поразить цель с координатами [х,у].

Задача 21

В сферической лунке прыгает шарик упруго ударяясь о ее стенки в двух точках, расположенных на одной горизонтали. Промежуток времени между ударами при движении шарика слева направо равен Т₁, а справа налево Т₂. Определите радиус лунки.

Определите скорость и ускорение, которыми обладают точки земной поверхности на экваторе и в Санкт-Петербурге из-за вращения Земли вокруг своей оси. Радиус Земли принять равным 6400 км. Санкт-Петербург находится на 60° с.ш.

Край гладкого горизонтального стола скруглен по окружности радиуса r. С какой наименьшей скоростью нужно пустить по столу маленькое тело, чтобы оно, достигнув начала скругления, сразу полетело по параболе?

Преобразование Галилея.

Занятие 5

Начальные положения и скорости двух кораблей заданы на рисунке. Корабли движутся без ускорения. Найдите наименьшее расстояние между ними.

Буер представляет собой сани с парусом, и может двигаться лишь по прямой, вдоль которой направлены его коньки. Ветер дует со скоростью v перпендикулярно направлению движения буера. Парус отклонен на 30° относительно направления движения буера. Какую максимальную скорость может развить буер в таких условиях?

При упругом ударе тела о неподвижную стенку его скорость v меняется лишь по направлению. Определите изменение скорости после удара этого тела, если стенка движется: со скоростью u навстречу телу; со скоростью w F.

На плоскости, тангенс угла наклона которой равен коэффициенту трения, лежит монетка. В горизонтальном направлении вдоль плоскости монете сообщили скорость v. Найдите установившуюся скорость монеты.

Занятие 4

Найдите ускорение тел системы изображенной на рисунке. Сила F приложена в направлении нити к одному из тел массы m. Участки нити по обе стороны от легкого блока, прикрепленного к телу массы M, параллельны.

Задача 20

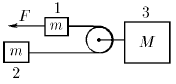
К свободному концу нити, прикрепленной к стенке и переброшенной через ролик, подвешен груз. Ролик закреплен на бруске массы m₀, который может скользить по горизонтальной плоскости без трения. В начальный момент нить с грузом отклоняют на угол α от вертикали, а затем отпускают. Определите ускорение бруска, если известно, что угол, образованный нитью с вертикалью, не меняется при движении системы. Чему равна масса груза?

Скорость тела массы m в жидкости убывает с пройденным расстоянием l по закону , где –начальная скорость, а β – постоянный коэффициент. Как зависит сила вязкого трения, действующая на тело со стороны жидкости, от скорости тела?

Сила сопротивления воздуха, действующая на капли дождя, пропорциональна произведению квадрата скорости капель на квадрат их радиуса: , где ρ – плотность воздуха, а безразмерный коэффициент равен приблизительно 0,16 (а α 0,3). Какие капли, крупные или мелкие, падают на землю с большей скоростью? Оцените скорость капли радиусом в 1мм при падении с большой высоты.

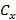
Сила сопротивления воздуха, действующая на капли тумана, пропорциональна произведению радиуса на скорость: . Капли радиуса 0,1 мм падая с большой высоты имеют скорость порядка 1 м/с. Какую скорость будут иметь капли, радиус которых в два раза меньше? А в десять раз?

Занятие 5

Задача 24

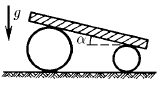
На два катка разного радиуса положи тяжелую плиту. Она образует угол α с горизонтом. Найдите ускорение этой плиты. Проскальзывания нет. Масса катков в сравнении с массой плиты мала.

Тело массы M связано нитью длины l с осью, вокруг которой оно обращается с угловой скоростью ω. Найдите силу натяжения нити. Размером тела и силой тяжести пренебречь. Замените нить однородной веревкой массы m и найдите зависимость силы натяжения веревки от расстояния x от оси вращения.

На гладкое проволочное кольцо радиуса R, расположенное вертикально, надета маленькая бусинка массы m, которая может скользить по кольцу без трения. Кольцо вращается с угловой скоростью ω вокруг вертикальной оси, проходящей по диаметру кольца. Где находится бусинка?

Из тонкого резинового жгута массы m и жесткости k сделали кольцо радиуса R₀. Это кольцо раскрутили вокруг его оси. Найдите новый радиус кольца, если угловая скорость его вращения ω.

Занятие 6

Задача 28

Кольцевая цепочка массы m надета на горизонтальный диск радиуса R. Сила натяжения надетой цепочки равна T. Найдите коэффициент трения между диском и цепочкой, если при вращении диска с угловой скоростью равной или большей ω, цепочка с него спадает.

Конькобежец на ледяной дорожке старается пройти вираж как можно ближе к внутренней бровке. Велосипедист на велотреке, наоборот, проходит вираж как можно дальше от внутренней бровки. Как объяснить это различие в тактике прохождения виража? Профиль велотрека все круче по мере удаления от внутренней бровки.

В цирковом аттракционе мотоциклист движется по внутренней поверхности сферы радиуса R. Разогнавшись, он начинает описывать горизонтальную окружность в верхней полусфере. После этого, для пущего эффекта нижнюю полусферу убирают. Определите минимальную скорость мотоциклиста, если коэффициент трения шин о поверхность сферы равен μ, а угол между вертикалью и направлением к мотоциклисту из центра сферы равен α.

С какой угловой скоростью должен вращаться вокруг своей оси горизонтально расположенный цилиндр, чтобы мелкие частицы внутри цилиндра не соскальзывали с его поверхности? Коэффициент трения между поверхностью цилиндра и частицами µ=1, внутренний радиус цилиндраR.

Импульс. Центр масс.

Занятие 1

Частица массы m движется со скоростью v, а частица массы 2m движется со скоростью 2v в направлении, перпендикулярном направлению движения первой частицы. На каждую частицу начинают действовать одинаковые силы. После прекращения действия сил первая частица движется со скоростью 2v в направлении, обратном первоначальному. Определить скорость второй частицы.

В масс-пролетном спектрометре источник испускает сгусток заряженных частиц, которые сначала летят свободно, и пролетают первый датчик D₁, находящийся на расстоянии Lот сетки. За сеткой, по нормали к ней, на частицы действует электрическая сила F. Частицы поворачиваются и вылетают через сетку назад, пролетая через второй датчик D₂, находящийся на том же расстоянии от сетки. От напряжения источника зависит скорость вылетающих частиц, но точное ее значение остается неизвестным. Меняя напряжения, измеряют время между срабатываниями датчиков и находят наименьшее его значение Δt. Какова масса частицы? Как можно найти массу частиц, если источник испускает несколько сортов частиц с разной массой?

Ящик с песком массы M лежит на горизонтальной плоскости, коэффициент трения с которой равен µ. Под углом α к вертикали в ящик со скоростью v влетает пуля массы m и почти мгновенно застревает в песке. Через какое время после попадания пули в ящик, он, начав движение, остановится? При каком значении α он вообще не сдвинется?

При наблюдениях с Земли удается определить только радиальную скорость звезд-партнеров, входящих в состав двойной звезды. При измерениях получены значения радиальной скорости v₁иu₁ звезд партнеров двойной звезды. При повторных измерениях, проведенных через год, значения этой скорости составили v₂и u₂. Найдите отношения масс звезд, входящих в состав двойной звезды. Почему нужно изменить расчеты, если повторное измерение проводится через день, месяц или полгода?

На покоящееся тело массы m₁налетает со скоростью v тело массы m₂. Сила, возникающая при взаимодействии тел, линейно зависящая от времени, растет от нуля до значения F₀за время t₀, а затем равномерно убывает до нуля за то же время. Определите скорости тел после взаимодействия, считая, что движение происходит по одной прямой.

Космический корабль перед отделением последней ступени ракеты-носителя имел скорость v, после отбрасывания последней ступени его скорость стала равной 1.01v, при этом отделившаяся ступень удаляется от корабля со скоростью 0.04v. Какова масса последней ступени, если масса корабля m₀?

Протон с начальной скоростью v летит прямо на первоначально покоящееся ядро гелия. Какова скорость частиц при наибольшем их сближении? Масса ядра гелия близка к учетверенной массе протона.

При β-распаде покоящегося первоначально нейтрона образуются протон, электрон и нейтрино. Импульсы протона и электрона равны p₁иp₂, угол между ними α. Определите импульс нейтрино.

Занятие 2

Где находится центр масс однородного прута, согнутого посередине под прямым углом? Однородной треугольной пластинки?

На первоначально неподвижной тележке установлены два вертикальных цилиндрических сосуда, соединенных тонкой трубкой. Площадь сечения каждого сосуда равна S, расстояние между их осями l. Один из сосудов заполнен жидкостью плотности ρ. Кран на соединительной трубке открывают. Найдите скорость тележки в момент времени, когда скорость уровня жидкости равна v. Полная масса системы равна m.

На гладком полу стоит сосуд заполненный водой плотности ρ₀, объем воды в сосуде V₀. Оказавшийся на дне сосуда жук объема V и плотности ρначинает ползти по дну сосуда со скоростью u относительно него. С какой скоростью станет двигаться сосуд по полу? Массой сосуда пренебречь, уровень воды все время остается горизонтальным.

Два тела массы m₁и m₂связаны натянутой нитью длины l и движутся по гладкой горизонтальной поверхности. В некоторый момент времени оказалось, что тело массы m₁неподвижно, а другое тело движется со скоростью v перпендикулярно нити. Определите силу натяжения нити.

Космическая станция состоит из двух отсеков массы m₁и m₂, соединенных длинным однородным тросом длины L. Станция вращается вокруг своей оси, перпендикулярной тросу. Какова угловая скорость вращения, если сила натяжения троса вблизи первого отсека равна T₁, а вблизи второго T₂? Какова масса троса?

Три точечные массы m₁, m₂, m₃ связаны нитями длины l и вращаются с угловой скоростью ω вокруг центра масс сохраняя конфигурацию равностороннего треугольника. Найдите силу натяжения всех нитей.

Занятие 3

На тележке установлен цилиндрический сосуд с площадью сечения S, наполненный жидкостью плотности ρ. От сосуда, параллельно полу, отходит тонкая горизонтальная трубка длины L, небольшой отрезок которой загнут по вертикали вниз. Уровень жидкости в сосуде опускается с ускорением a. Какой горизонтальной силой можно удержать тележку на месте?

Задача 17

Обезьяна массы m уравновешена противовесом на блоке A. Блок A уравновешен грузом массы 2m на блоке B. В исходном состоянии система неподвижна. Обезьяна начинает равномерно выбирать веревку со скоростью u относительно себя. Как будут двигаться грузы? Массой блоков и трением пренебречь.

На тросе висит небольшой ящик с песком. В ящик стреляют из пулемета и пули застревают в песке. Скорость пули v, масса пули m, масса ящика с песком M. Трос отклоняется на угол α от вертикали. Какова скорострельность пулемета, если все выпущенные пули попадают в цель?

В цилиндре под поршнем массы M прыгают, упруго ударяясь о поршень и дно цилиндра, N>>1 шариков массы m каждый. Сила тяжести, действующая на поршень, уравновешена ударами шариков. Расстояние между дном цилиндра и поршнем равно h. Полная энергия каждого шарика одинакова. На какую высоту будут подскакивать шарики, если поршень мгновенно убрать (за время поднятия поршня не произойдет столкновений между шариками и поршнем)?

Две тележки массы M каждая движутся параллельно со скоростями v1 и v2. Груз массы m, сначала лежавший на первой тележке, с почти нулевой скоростью относительно этой тележки перебрасывают на вторую тележку. Затем с почти нулевой скоростью уже относительно второй тележки его перебрасывают обратно на первую. Какой станет разность скоростей тележек после N таких перебросов груза туда и обратно?

Задача 21

Веревку, перекинутую через гладкий гвоздь, протаскивают со скоростью v сквозь щель. Сила трения в щели F, масса единицы длины веревки ρ. Определите силу, действующую на гвоздь, если участки веревки по разные стороны гвоздя образуют угол α. При какой скорости веревка отойдет от гвоздя?

Газ, вытекающий из сопла ракеты, имеет скорость v относительно нее. Определите изменения скорости ракеты после того, как ее масса из-за истечения газа уменьшилась в n раз.