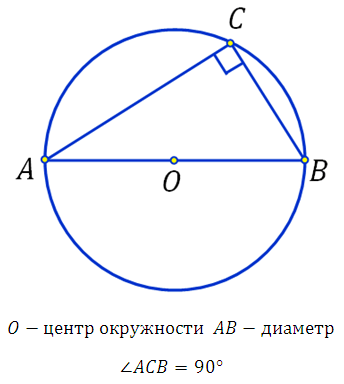
Окружность описанная около прямоугольного треугольника. В этой публикации мы с вами рассмотрим доказательство одного «математического факта», который широко используется при решении задач по геометрии. В одних источниках сей факт обозначается как теорема, в других как свойство, формулировки имеются разные, но суть их одна:
Любой треугольник построенный на диаметре окружности, третья вершина которого лежит на этой окружности является прямоугольным!
То есть закономерность в этом геометрическом узоре состоит в том, что, куда бы вы ни поместили вершину треугольника, угол при этой вершине всегда будет прямым:
Заданий присутствующих с составе экзамена по математике, в ходе решений которых используется это свойство, достаточно много.
Стандартное доказательство считаю весьма путанным и перегруженным математическими символами, его вы найдёте в учебнике. Мы же рассмотрим простое и интуитивно понятное. Его я обнаружил в одном замечательном эссе под названием » Плач математика «, рекомендую к прочтению учителям и ученикам.
Сначала вспомним некоторые теоретические моменты:
Признак параллелограмма. У параллелограмма противолежащие стороны равны. То есть если у четырехугольника обе пары противолежащих сторон равны, то этот четырехугольник – параллелограмм.
Признак прямоугольника. Прямоугольник является параллелограммом, и его диагонали равны. То есть если у параллелограмма диагонали равны, то он является прямоугольником.
*Прямоугольник является параллелограммом, это его частный случай.
Возьмем треугольник и относительно центра окружности повернем его на 180 0 (перевернём его). У нас получится четырехугольник, вписанный в окружность:
Поскольку мы просто повернули треугольник, то противолежащие стороны четырехугольника равны, значит это параллелограмм. Поскольку треугольник повернут ровно на 180 градусов, значит его вершина диаметрально противоположна вершине «исходного» треугольника.
Получается, что диагонали четырёхугольника равны, так они являются диаметрами. Имеем четырёхугольник у которого противолежащие стороны равны и диагонали равны, следовательно это есть прямоугольник, а у него все углы прямые.
Вот и всё доказательство!
Можно рассмотреть и такое, тоже простое и понятное:
Из точки С построим отрезок проходящий через центр окружности, другой конец которого будет лежать на противоположной точке окружности (точка D). Точку D соединим с вершинами А и В: 
Получили четырёхугольник. Треугольник АОD равен треугольнику СОВ по двум сторонам и углу между ними:
Из равенства треугольников следует, что AD = CB.
Аналогично и АС = DB.
Можем сделать вывод, что четырёхугольник является параллелограммом. Кроме того, его диагонали равны – АВ изначально дан как диаметр, СD также диаметр (проходит через точку О).
Таким образом, АСВD прямоугольник, значит все его углы прямые. Доказано!
Ещё один примечательный подход, который ярко и «красиво» говорит нам о том, что рассматриваемый угол всегда прямой.
Посмотрите и вспомните информацию про вписанный угол . А теперь посмотрите на эскиз:
Угол АОВ не что иное как центральный угол опирающийся на дугу АDB, и равен он 180 градусам. Да, АВ это диаметр окружности, но ничто нам не мешает считать АОВ центральным углом (это развёрнутый угол). Угол же АСВ является вписанным для него, он опирается также же дугу на АDB.
А мы знаем, что вписанный угол равен половине центрального, то есть как бы мы не разместили точку С на окружности, угол АСВ всегда будет равен 90 градусам, то является прямым.
Какие выводы можно сделать применительно к решению задач, в частности включённых в экзамен?
Если в условии речь идёт о треугольнике вписанном в окружность и построенном на диаметре этой окружности, то однозначно этот треугольник является прямоугольным.
Если сказано, что прямоугольный треугольник вписан в окружность, то это означает, что его гипотенуза является совпадает с её диаметром (равна ему) и центр гипотенузы совпадает с центром окружности.
Видео:№694. Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенузаСкачать
Please wait.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать
We are checking your browser. mathvox.ru
Видео:ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6cd5ab5acfb58e77 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:№171. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскостиСкачать
Прямоугольный треугольник
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами .
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).
Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где 
– катеты, 
– гипотенуза. Видеодоказательство
4. Площадь 
прямоугольного треугольника с катетами :
5. Высота 
прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус 
описанной окружности есть половина гипотенузы :
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус 
вписанной окружности выражается через катеты и гипотенузу следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
🔍 Видео
ЛАЙФХАК ПРО РАДИУС ОПИСАННОЙ ОКРУЖНОСТИ 🔥 #огэ #егэ #геометрия #математикаСкачать
Найдите гипотенузуСкачать
Треугольник и окружность #shortsСкачать
ЗАДАНИЕ 1| ЕГЭ ПРОФИЛЬ| Радиус окружности, описанной около прямоугольного треугольника, равен 4. НайСкачать
3 задача по геометрии на ЕГЭ / Как решается геометрическая задача на ЕГЭ 2021 по математике?Скачать
Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать
Гипотенуза прямоугольного треугольникаСкачать
Задание №17 ОГЭ 2020 Математика Окружность радиусСкачать
№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать
Прямоугольный треугольник и описанная окружностьСкачать
Задание 25 Прямоугольный треугольник Вписанная описанная окружностиСкачать
Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу.Скачать
Вписанная и описанная окружность - от bezbotvyСкачать
Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать
Медиана в прямоугольном треугольникеСкачать
