Геометрическое место точек окружность и круг презентация

презентация к уроку

Видео:Геометрическое место точек окружность и круг - 7 класс геометрияСкачать

Скачать:

Предварительный просмотр:

Видео:Геометрическое место точек (ГМТ).ОКРУЖНОСТЬ и КРУГ §19 геометрия 7 классСкачать

Подписи к слайдам:

Урок геометрии в 7 классе по теме: «Окружность»

Цели урока : ввести понятие определения; систематизировать сведения об окружности, известные учащимся из курса математики предыдущих классов; уделить особое внимание отработке определения окружности и ее элементов.

Анализ самостоятельной работы и ее итоги.

Вводная беседа «В мире окружностей».

Работа с учебником по изучению материала. Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности. Отрезок, соединяющий центр с какой либо точкой окружности – радиусом окружности. О

Отрезок, соединяющий две точки окружности, называется ее хордой . Хорда, проходящая через центр окружности, называется диаметром . О А В С D

Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. А В М О С

О Часть плоскости, ограниченная окружностью, называется кругом . У круга есть одна подруга, Знакома всем её наружность: Она идет по краю круга И называется окружность.

По готовым рисункам определить радиусы, хорды, диаметры, дуги, полуокружности

Проверка усвоения изученного материала Решить задачи №143 (устно), 144, 147.

Построения циркулем и линейкой. Построение угла равного данному А О М

Провести окружность произвольного радиуса с центром в вершине А. А С В

Провести окружность того же радиуса с центром в начале данного луча ОМ. Провести окружность с центром в точке D радиуса ВС. Вывод: треугольники АВС и О D Е равны (по третьему признаку), т.е. построенный угол МОЕ равен данному углу А. Решение

Построение биссектрисы угла. А

Решение Провести окружность произвольного радиуса с центром в точке А. Провести две окружности одинакового радиуса ВС с центрами в точках В и С. Рассмотреть треугольники АСЕ и АВЕ (они равны по трем сторонам). Вывод: угол САЕ равен углу ВАЕ, т.е. луч АЕ биссектриса данного угла ВАС

Самостоятельная работа I вариант Отрезки КМ и EF являются диаметрами окружности с центром О. Докажите, что: а)угол FEM равен углу KME ; б) КЕ и MF равны. II вариант Отрезки ME и РК являются диаметрами окружности с центром О. Докажите, что: а)угол ЕМР равен углу MPK ; б) отрезки МК и РЕ равны.

Итоги урока. Что повторили на уроке? Что узнали нового?

Домашнее задание П.21, вопросы 16 (стр.50), задачи №145, 146 .

Видео:ГМТ // ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕКСкачать

По теме: методические разработки, презентации и конспекты

Презентация «Геометрическое место точек»

Презентация к уроку в 9 классе по теме «Геометрическое место точек».

Геометрические места точек.Элективный курс

Элективный курс в рамках предпрофильной подготовки.

Геометрическое место точек. Презентация к уроку

Задачи на ГМТ нечасто встречаются в школьной программе, но решение их развивает математический кругозор.

Геометрическое место точек. Окружность и круг

Сформировать представление учащихся о геометрическом месте точек, изучить свойство серединного перпендикуляра, свойство биссектрисы угла, дать понятие окружности, круга и их элементов.Формировать отве.

Презентация Геометрическое место точек

Презентация для 7 класса Геометрическое место точек.

Технологическая карта урока геометрии 7 класс » Геометрическое место точек. Окружность и круг»

Технологическая карта урока геометрии 7 класс по теме: «Геометрическое место точек. Окружность и круг&quot.

Видео:Окружность. 7 класс.Скачать

Презентация. Геометрия 7 класс. Геометрическое место точек

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Тема урока: Геометрическое место точек Геометрия – 7 класс Велиханова Марина Александровна, учитель математики КГУ «Банновская средняя школа», отдела образования акимата Федоровского района

Цели обучения: 7.1.1.31 знать определение геометрического места точек

Геометрическое место – термин, применявшийся в старой литературе по геометрии и до сих пор применяющийся в учебной литературе, для обозначения множества точек, удовлетворяющих некоторому условию, как правило, геометрического характера. Определение. Геометрическое место точек (сокращённо ГМТ) — это фигура, состоящая из всех точек плоскости, которые обладают некоторым свойством.

1) На отрезке АВ найдите геометрическое место точки, равноудаленной от его концов. Геометрическое место точки, находящейся на отрезке и равноудаленной от его концов, есть середина отрезка. А В

2) Что представляет собой геометрическое место точек, равноудаленных от концов отрезка? А В

2) Что представляет собой геометрическое место точек, равноудаленных от концов отрезка? Геометрическое место точек, равноудаленных от концов отрезка – серединный перпендикуляр к отрезку А В

О 6 см 3)Как выглядит геометрическое место точек, удаленных на расстояние 6 см от точки О? Геометрическое место точек, удаленных на определенное расстояние от заданной точки — это окружность с центром в заданной точке.

6 см О 4) Как выглядит ГМТ, расстояние от которых до заданной точки не больше 6 см? Кругом называют ГМТ, расстояние от которых до заданной точки не больше данного положительного числа.

Задачи на нахождение ГМТ Решение задачи на поиск ГМТ должно содержать доказательство того, что все точки фигуры, указанной в ответе, обладают требуемым свойством, а также наоборот, что все точки, обладающие требуемым свойством, принадлежат этой фигуре

Задача. Доказать, что биссектриса угла есть геометрическое место точек, равноудаленных от его сторон. 1) Построим CDBC, ADBA 2) BD-биссектриса CBD=ABDBCD=BAD AD = CD 3)KM = EM – доказывается аналогично А В С D M E K

ЗАПОМНИТЕ Самые известные примеры ГМТ. Геометрическое место точек, равноудаленных от концов отрезка, — серединный перпендикуляр к отрезку. Геометрическое место точек, удаленных от данной точки на заданное положительное расстояние, — окружность Геометрическое место внутренних точек угла, равноудаленных от его сторон, — биссектриса угла.

Задания для самостоятельной работы Желаю успеха!

Задание 1. Ответьте на вопросы. 1) Что, на ваш взгляд, является геометрическим местом точек, равноудаленным от данной точки? 2) Что будет являться геометрическим местом точек, равноудаленных от сторон угла? 3) Дайте определение геометрического места точек, равноудаленных от концов данного отрезка.

Задание 2. По рисункам а), б), в) закончите предложения: а) Прямая a — геометрическое место точек, равноудаленных от. б) Луч BD — геометрическое место точек, равноудаленных от. в) Прямая a — геометрическое место точек, равноудаленных от.

Задание 3. Можно ли круг радиуса 5 см считать геометрическим местом точек, удаленных от центра этого круга на расстояние: А) длиной 5 см; Б) не больше 5 см; В) не менее 5 см; Г) не больше 4 см? Нет Да Нет Нет

Задание 4. Отрезок AB равен 4 см. Можно ли считать срединный перпендикуляр этого отрезка геометрическим местом точек, которые: А) удалены от A и B на 2 см; Б) удалены от A и B на одинаковые расстояния; В)* являются вершинами равнобедренных треугольников с основанием AB? Нет Да Да

На уроке мы Познакомились с определением геометрического места точек Изучили самые известные пример ГМТ Рассмотрели задания на нахождение ГМТ

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 937 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 496 195 материалов в базе

Материал подходит для УМК

«Геометрия», Погорелов А.В.

48. Геометрическое место точек

Видео:Математика 5 класс (Урок№26 - Окружность и круг. Сфера и шар.)Скачать

Дистанционные курсы для педагогов

Другие материалы

• 29.03.2020
• 447

• 28.03.2020
• 117

• 25.03.2020
• 136

• 24.03.2020
• 494

• 21.03.2020
• 341

• 10.03.2020
• 733

• 06.03.2020
• 1809

• 05.03.2020
• 806

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 02.04.2020 3304 —> —> —> —>
• PPTX 155 кбайт —> —>
• Оцените материал:

Настоящий материал опубликован пользователем Велиханова Марина Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 4 месяца
• Подписчики: 0
• Всего просмотров: 36221
• Всего материалов: 18

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:5 класс, 22 урок, Окружность и кругСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Орловские школы переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Школы Сургута переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Крупнейшие вузы Татарстана откроют цифровые кафедры в 2022 году

Время чтения: 1 минута

Санкт-Петербургский госуниверситет переходит на дистанционное обучение

Время чтения: 1 минута

Число иностранных студентов в РФ увеличилось за три года

Время чтения: 1 минута

Минпросвещения России запускает конкурс для учителей физкультуры

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрическое место точек. Окружность и круг.

В данной презентации представлено изложение нового материала по теме «Геометрическое место точек. Окружность и круг».

Просмотр содержимого документа
«Геометрическое место точек. Окружность и круг.»

Геометрическое место точек. Окружность и круг.

Геометрия 7 кл. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир.

Презентацию подготовила Григорьева С.В.

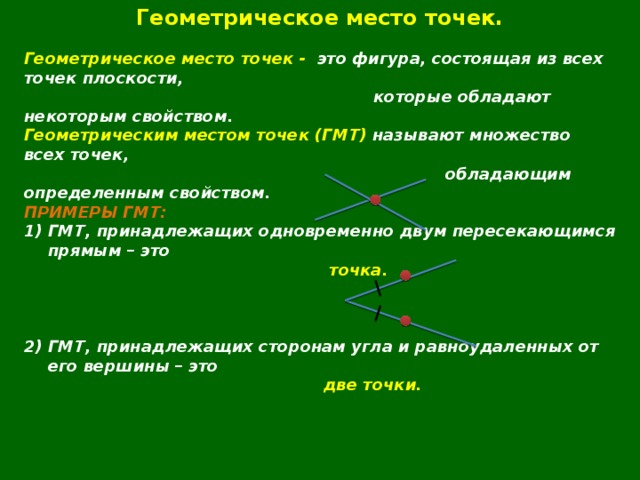
Геометрическое место точек.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

1) ГМТ, принадлежащих одновременно двум пересекающимся прямым – это

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

1) ГМТ, принадлежащих одновременно двум пересекающимся прямым – это

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

1) ГМТ, принадлежащих одновременно двум пересекающимся прямым – это

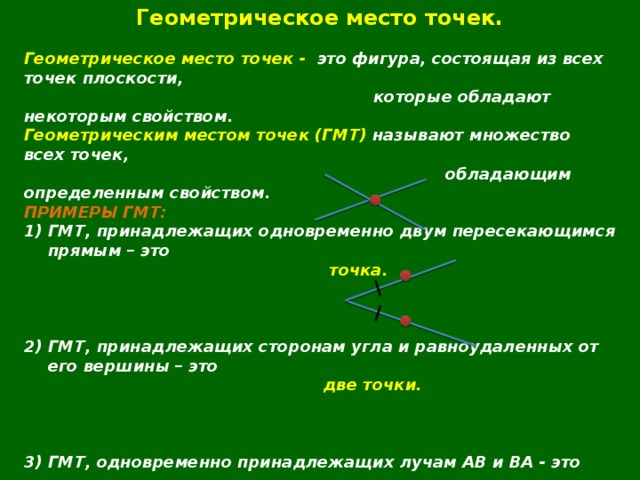
2) ГМТ, принадлежащих сторонам угла и равноудаленных от его вершины – это

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

1) ГМТ, принадлежащих одновременно двум пересекающимся прямым – это

2) ГМТ, принадлежащих сторонам угла и равноудаленных от его вершины – это

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

1) ГМТ, принадлежащих одновременно двум пересекающимся прямым – это

2) ГМТ, принадлежащих сторонам угла и равноудаленных от его вершины – это

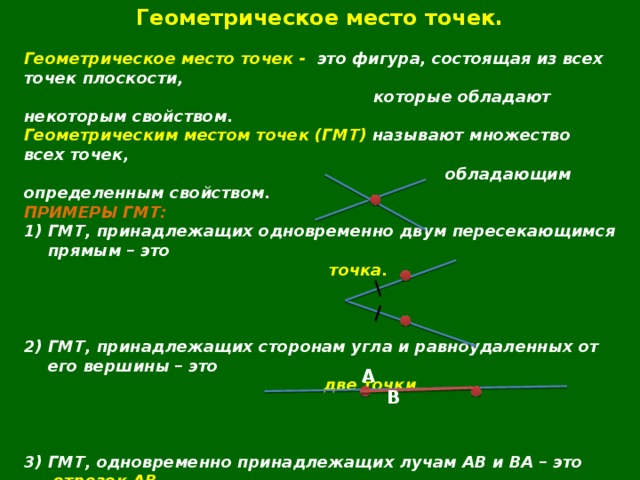
3) ГМТ, одновременно принадлежащих лучам АВ и ВА — это

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

1) ГМТ, принадлежащих одновременно двум пересекающимся прямым – это

2) ГМТ, принадлежащих сторонам угла и равноудаленных от его вершины – это

3) ГМТ, одновременно принадлежащих лучам АВ и ВА – это отрезок АВ

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

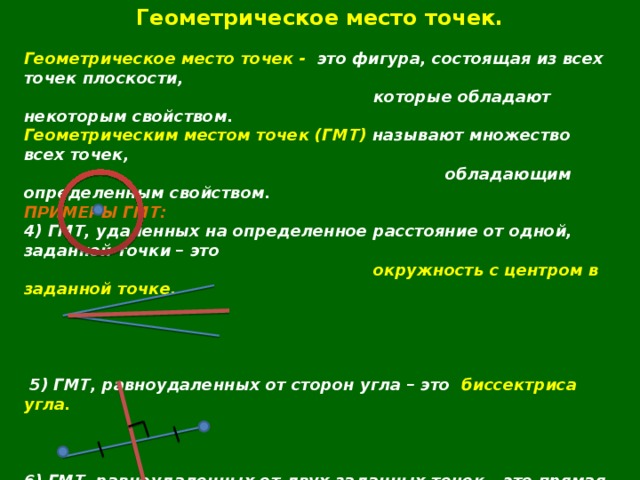
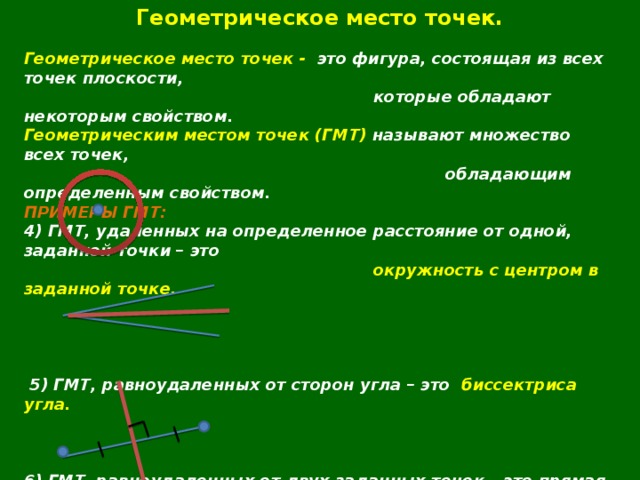
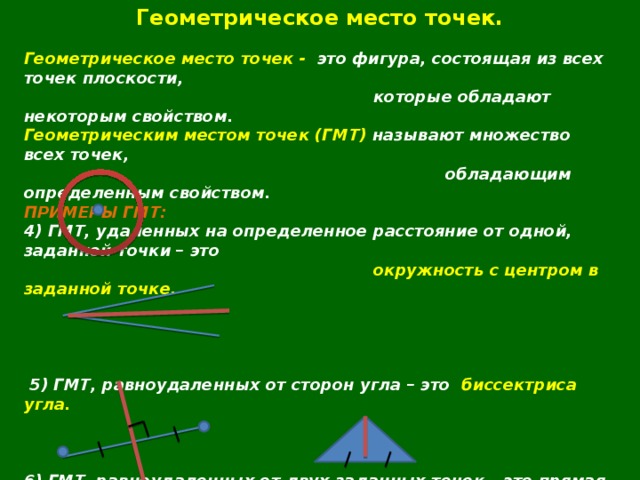
4) ГМТ, удаленных на определенное расстояние от одной, заданной точки – это

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

4) ГМТ, удаленных на определенное расстояние от одной, заданной точки – это

окружность с центром в заданной точке.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

4) ГМТ, удаленных на определенное расстояние от одной, заданной точки – это

окружность с центром в заданной точке.

5) ГМТ, равноудаленных от сторон угла – это

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

4) ГМТ, удаленных на определенное расстояние от одной, заданной точки – это

окружность с центром в заданной точке.

5) ГМТ, равноудаленных от сторон угла – это биссектриса угла.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

4) ГМТ, удаленных на определенное расстояние от одной, заданной точки – это

окружность с центром в заданной точке.

5) ГМТ, равноудаленных от сторон угла – это биссектриса угла.

6) ГМТ, равноудаленных от двух заданных точек – это

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

4) ГМТ, удаленных на определенное расстояние от одной, заданной точки – это

окружность с центром в заданной точке.

5) ГМТ, равноудаленных от сторон угла – это биссектриса угла.

6) ГМТ, равноудаленных от двух заданных точек – это прямая, проходящая через середину отрезка, соединяющего эти точки, перпендикулярно отрезку —

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

4) ГМТ, удаленных на определенное расстояние от одной, заданной точки – это

окружность с центром в заданной точке.

5) ГМТ, равноудаленных от сторон угла – это биссектриса угла.

6) ГМТ, равноудаленных от двух заданных точек – это прямая, проходящая через середину отрезка, соединяющего эти точки, перпендикулярно отрезку —

серединный перпендикуляр к отрезку ,

соединяющему данные точки.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Геометрическим местом точек (ГМТ) называют множество всех точек,

обладающим определенным свойством.

4) ГМТ, удаленных на определенное расстояние от одной, заданной точки – это

окружность с центром в заданной точке.

5) ГМТ, равноудаленных от сторон угла – это биссектриса угла.

6) ГМТ, равноудаленных от двух заданных точек – это прямая, проходящая через середину отрезка, соединяющего эти точки, перпендикулярно отрезку —

серединный перпендикуляр к отрезку ,

соединяющему данные точки.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что фигура является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

удаленных на определенное расстояние от одной, заданной точки.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

удаленных на определенное расстояние от одной, заданной точки.

— фигура, состоящая из всех точек плоскости,

удаленных на определенное расстояние от одной, заданной точки.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

удаленных на определенное расстояние от одной, заданной точки .

— фигура, состоящая из всех точек плоскости,

удаленных на определенное расстояние от одной, заданной точки.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

удаленных на определенное расстояние от одной, заданной точки.

— фигура, состоящая из всех точек плоскости,

удаленных на определенное расстояние от одной, заданной точки.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от сторон угла – это биссектриса угла. (В учебнике – это Теорема 19.2)

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от сторон угла – это биссектриса угла. (В учебнике – это Теорема 19.2)

1) Точка принадлежит биссектрисе угла =˃ она равноудалена от сторон этого угла.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от сторон угла – это биссектриса угла. (В учебнике – это Теорема 19.2)

1) Точка принадлежит биссектрисе угла =˃ она равноудалена от сторон этого угла.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от сторон угла – это биссектриса угла. (В учебнике – это Теорема 19.2)

1) Точка принадлежит биссектрисе угла =˃ она равноудалена от сторон этого угла.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от сторон угла – это биссектриса угла. (В учебнике – это Теорема 19.2)

• Точка принадлежит биссектрисе угла =˃ она равноудалена от сторон этого угла.

Рассмотрим Δ АОК и Δ ВОК — прямоугольные.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от сторон угла – это биссектриса угла. (В учебнике – это Теорема 19.2)

• Точка принадлежит биссектрисе угла =˃ она равноудалена от сторон этого угла.

Рассмотрим Δ АОК и Δ ВОК — прямоугольные.

ОК – общая гипотенуза, ˂АОК = ˂ ВОК по условию

(т.к. ОК – биссектриса), значит Δ АОК = Δ ВОК

=˃ АК = КВ как соответственные стороны

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от сторон угла – это биссектриса угла. (В учебнике – это Теорема 19.2)

2) Точка равноудалена от сторон угла (равны перпендикуляры) =˃ она принадлежит биссектрисе.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от сторон угла – это биссектриса угла. (В учебнике – это Теорема 19.2)

2) Точка равноудалена от сторон угла (равны перпендикуляры) =˃ она принадлежит биссектрисе.

Рассмотрим Δ DОК и Δ EОК — прямоугольные.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от сторон угла – это биссектриса угла. (В учебнике – это Теорема 19.2)

2) Точка равноудалена от сторон угла (равны перпендикуляры) =˃ она принадлежит биссектрисе.

Рассмотрим Δ DОК и Δ EОК — прямоугольные.

Итак, доказали, что Δ DОК = Δ EОК по гипотенузе и

катету =˃ ˂ DOK = ˂ EOK как соответственные, т.о.

ОК принадлежит биссектрисе ˂ DOE.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от концов отрезка –

это серединный перпендикуляр к отрезку. (В учебнике — это Теорема 19.1)

1) Точка принадлежит серединному перпендикуляру =˃

равноудалена от концов отрезка.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от концов отрезка –

это серединный перпендикуляр к отрезку. (В учебнике — это Теорема 19.1)

1) Точка принадлежит серединному перпендикуляру =˃

равноудалена от концов отрезка.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от концов отрезка –

это серединный перпендикуляр к отрезку. (В учебнике — это Теорема 19.1)

1) Точка принадлежит серединному перпендикуляру =˃

равноудалена от концов отрезка.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от концов отрезка –

это серединный перпендикуляр к отрезку. (В учебнике — это Теорема 19.1)

1) Точка принадлежит серединному перпендикуляру =˃

равноудалена от концов отрезка.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от концов отрезка –

это серединный перпендикуляр к отрезку. (В учебнике — это Теорема 19.1)

1) Точка принадлежит серединному перпендикуляру =˃

равноудалена от концов отрезка.

По доказанному устно: АК = КВ, т.е. точка К –

равноудалена от концов отрезка. Ч.т.д.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от концов отрезка –

это серединный перпендикуляр к отрезку. (В учебнике — это Теорема 19.1)

1) Точка принадлежит серединному перпендикуляру =˃

равноудалена от концов отрезка.

По доказанному устно: АК = КВ, т.е. точка К –

равноудалена от концов отрезка. Ч.т.д .

2) Точка равноудалена от концов отрезка =˃

принадлежит серединному перпендикуляру.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от концов отрезка –

это серединный перпендикуляр к отрезку. (В учебнике — это Теорема 19.1)

1) Точка принадлежит серединному перпендикуляру =˃

равноудалена от концов отрезка.

По доказанному устно: АК = КВ, т.е. точка К –

равноудалена от концов отрезка. Ч.т.д .

2) Точка равноудалена от концов отрезка =˃

принадлежит серединному перпендикуляру.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Геометрическое место точек, равноудаленных от концов отрезка –

это серединный перпендикуляр к отрезку. (В учебнике — это Теорема 19.1)

1) Точка принадлежит серединному перпендикуляру =˃

равноудалена от концов отрезка.

По доказанному устно: АК = КВ, т.е. точка К –

равноудалена от концов отрезка. Ч.т.д .

2) Точка равноудалена от концов отрезка =˃

принадлежит серединному перпендикуляру.

По доказанному устно: т. К принадлежит серединному

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Сделаем вывод: описанные три примера, действительно являются примерами геометрических мест точек.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

• Найти на плоскости и обозначить несколько точек, обладающих заданным свойством;

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

• Найти на плоскости и обозначить несколько точек, обладающих заданным свойством;
• Сделать предположение о том, как размещена на плоскости искомая фигура;

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

• Найти на плоскости и обозначить несколько точек, обладающих заданным свойством;
• Сделать предположение о том, как размещена на плоскости искомая фигура;
• Доказать два взаимно обратных утверждения.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

• Найти на плоскости и обозначить несколько точек, обладающих заданным свойством;
• Сделать предположение о том, как размещена на плоскости искомая фигура;
• Доказать два взаимно обратных утверждения.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

• Найти на плоскости и обозначить несколько точек, обладающих заданным свойством;
• Сделать предположение о том, как размещена на плоскости искомая фигура;
• Доказать два взаимно обратных утверждения.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

• Найти на плоскости и обозначить несколько точек, обладающих заданным свойством;
• Сделать предположение о том, как размещена на плоскости искомая фигура;
• Доказать два взаимно обратных утверждения.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

• Найти на плоскости и обозначить несколько точек, обладающих заданным свойством;
• Сделать предположение о том, как размещена на плоскости искомая фигура;
• Доказать два взаимно обратных утверждения.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

• Найти на плоскости и обозначить несколько точек, обладающих заданным свойством;
• Сделать предположение о том, как размещена на плоскости искомая фигура;
• Доказать два взаимно обратных утверждения.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

• Найти на плоскости и обозначить несколько точек, обладающих заданным свойством;
• Сделать предположение о том, как размещена на плоскости искомая фигура;
• Доказать два взаимно обратных утверждения.

Геометрическое место точек.

Геометрическое место точек — это фигура, состоящая из всех точек плоскости,

которые обладают некоторым свойством.

Для доказательства того, что какое-то множество точек является Геометрическим местом точек, обладающих некоторым свойством, нужно доказать два взаимно-обратных утверждения:

• Каждая точка данного множества обладает заданным свойством;
• Если точка обладает заданным свойством, то она принадлежит данному множеству.

Для нахождения ГМТ, обладающих определенным свойством, нужно:

• Найти на плоскости и обозначить несколько точек, обладающих заданным свойством;
• Сделать предположение о том, как размещена на плоскости искомая фигура;
• Доказать два взаимно обратных утверждения.

Предположение: две прямые, параллельные прямой а

и находящиеся на расстоянии m от нее.

Геометрическое место точек.

Геометрическое место точек.

1. Теперь вы знаете, что называется Геометрическим местом точек.

Геометрическое место точек.

• Теперь вы знаете, что называется Геометрическим местом точек.
• Вы можете привести несколько примеров ГМТ, обладающего каким-то свойством. (Окружность, биссектриса, серединный перпендикуляр).

Геометрическое место точек.

• Теперь вы знаете, что называется Геометрическим местом точек.
• Вы можете привести несколько примеров ГМТ, обладающего каким-то свойством. (Окружность, биссектриса, серединный перпендикуляр).
• Вы умеете решать задачи, в которых нужно найти ГМТ, обладающее заданным свойством.

Геометрическое место точек.

Параграф 19, с.124 – 127 (до задачи),

🎥 Видео

Математика 26. Циркуль. Окружность и круг — Шишкина школаСкачать

7 класс | УРОК №1 | Геометрия. Геометрическое место точек.Окружность и кругСкачать

Окружность. Круг. 5 класс.Скачать

Окружность и круг | Математика 5 класс #22 | ИнфоурокСкачать

Окружность и круг, 6 классСкачать

Видеоурок 14. Круг и окружность. Математика 3 классСкачать

Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Найти центр кругаСкачать

7 класс, 21 урок, ОкружностьСкачать

Решение заданий по теме ГМТ. Окружность и круг.Скачать

Геометрическое место точекСкачать

ОКРУЖНОСТЬ и КРУГ. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ. Контрольная №4. 7 классСкачать