Геодезический купол схема из треугольников

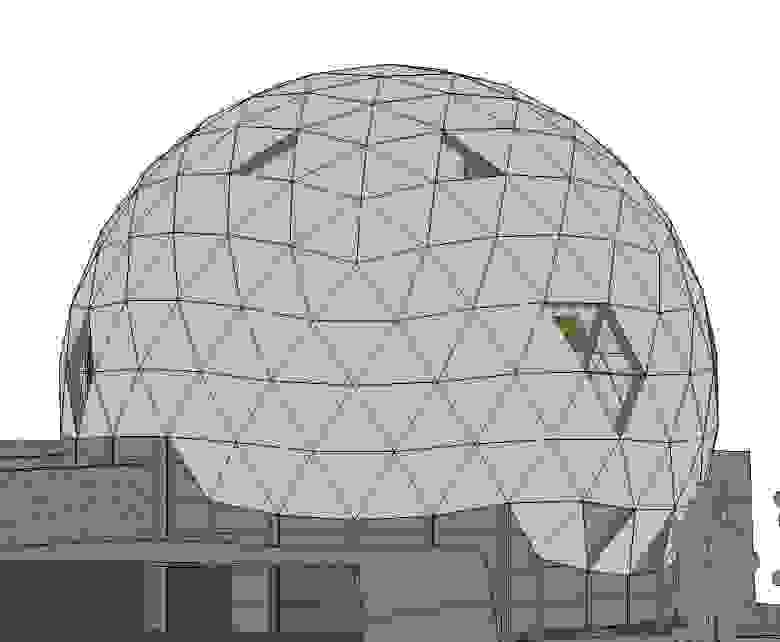
Теплица на даче давно стала не только подспорьем в выращивании овощей, но еще и возможностью реализовать свои творческие амбиции. Среди всех новаторских решений особого внимания заслуживает геодезический купол – детище современной архитектуры. Интерес к оригинальной конструкции объясняется просто – установить такую теплицу на своем участке под силу даже неопытному мастеру – полусфера легко собирается из простых деталей, а производительность ее грядок не уступает урожаям из стандартных сооружений.

Видео:купольная теплица своими руками (диаметр 6 метров)Скачать

Чем привлекательны конструкции в форме купола

Рост популярности купольных теплиц объясняется несколькими факторами:

1. Для установки не нужен прочный фундамент, так как ее конструкция значительно легче, чем аналогичные по площади привычные укрытия.
2. Сооружение легко монтируется и разбирается, при необходимости его несложно перенести на новое место.
3. Полусферическая форма отличается высокой прочностью и стабильностью. Ячеистый каркас лучше противостоит сильным ветрам, легко выдерживает снегопады и обладает хорошей сейсмоустойчивостью.
4. По сравнению с традиционными формами укрытий, строительство теплицы-купола обходится дешевле, так как для монтажа не требуется сложное оборудование. В строительстве используются простые доступные материалы – деревянные бруски или пластиковые трубки для каркаса, шурупы, поликарбонат, агроволокно или парниковую пленка для обшивки.
5. За счет уникальной секционной структуры отпадает необходимость в установке внутренних опор, а это существенно экономит стройматериалы.
6. В отличие от прямоугольных теплиц в полусфере, не нужно ориентировать грядки относительно сторон света – растения всегда хорошо освещены.

В геокуполе легко обеспечить необходимый микроклимат для выращивания нескольких урожаев огородных культур за год. Грунт всегда хорошо прогревается, а для поддержания стабильности температуры используются экологичные тепловые аккумуляторы – резервуары с водой.

Видео:SketchUp: Как создать геодезический купол?Скачать

Как самостоятельно построить купольную теплицу

Построить такое сооружение на своем участке несложно. Для этого потребуется рассчитать размеры секций, распечатать схему сборки, подготовить детали каркаса, расчистить место для установки теплицы и можно приступать к монтажу.

Принципы конструирования купольного каркаса

По своей сути все геодезические купола – это многогранники, грани которых образовывают поверхность, максимально приближенную по форме к сфере. Форма граней может быть разной, но треугольник считается самым стабильным и устойчивым. Поэтому в большинстве случаев основным структурным элементом для создания полусферического каркаса является треугольник.

Для строительства каркаса малых купольных строений на дачных участках – теплиц, беседок, гостевых домиков – чаще всего применяют каркасно-щитовую технологию на основе равнобедренных треугольников разного размера. Чем меньше размер секций, тем больше их потребуется для создания сферического парника. Принцип их соединения между собой похож на пошив футбольного мяча – треугольники соединяются в выпуклые шести- и пятиугольники, которые объединены в устойчивую полусферу.

Совет! Если при расчете геокупола не учитывались углы соединения фрагментов, то монтаж лучше проводить при помощи коннекторов с 4, 5 и 6 лопастями.

Формула расчета длины элементов купола

Чтобы не ошибиться в процессе сборки, нужно заранее все высчитать длину всех ребер, правильную последовательность их чередования, углы соединения элементов. Для составления оптимальной схемы необходимо пользоваться специальными формулами. В основу расчета геодезического купола ложатся конкретные размеры:

• радиус основы сооружения;
• высота теплицы (выраженная в дробном отношении к диаметру сферы, H);
• частота разбивки на секции (V).

Чем выше числовой индекс V (1, 2, 3…), тем больше типов ребер потребуется подготовить. Купол 1V – это усеченный икосаэдр, все ребра одной длины. Такое сооружение больше похоже на пирамиду с пятью гранями. Для строительства домашней теплицы лучше всего подходят купола 2V (два вида ребер, H= радиусу) и 3V (ребра А, В, С, высота сооружения Н= 5/8, 7/12, 5/12 диаметра).

Длина каждого вида ребер (La, Lв, Lс…) рассчитывается по формуле L=R*K, где R – это радиус основания каркаса, а K – коэффициент по частоте разбивки.

Для вычисления необходимого количества материала для обшивки используют формулу расчета площади сферы: S=2π *R*H, где R – радиус основания, а H – вычисленная высота теплицы. Например, при радиусе основания 3V теплицы 4 м и высоте 3/8d, расчет площади будет таким:

S=2*3,14*4*(3/8*8) = 75,36 м2

Подготовка к монтажу каркаса

При строительстве геодезического купола своими руками для каркаса нужно выбирать легкий и прочный материал – деревянные бруски, нетяжелые металлические пруты или пластиковые трубы. Деревянные бруски перед покраской лучше пропитать противогрибковым составом. При подготовке фрагментов крайне важно соблюдать точность разметки – все детали одного типа должны быть взаимозаменяемы.

Совет! Окрашивайте ребра одинаковой длины одним цветом. Например: ребра А – красные, В – синие, С – желтые. Для облегчения работы с цветной схемой сборки маркировка готовых ребер должна совпадать с маркировкой на чертеже.

Количество ребер по типам и коннекторов для монтажа каждого вида купола высчитывается по схемам.

Полевые работы и монтаж основания

Для установки геодезического купола на даче необходимо выбрать открытый незатененный участок. Плодородную почву с площадки можно временно удалить, а саму поверхность засыпать глиной и тщательно выровнять и утрамбовать. Если почва неустойчивая, то под основание придется залить небольшой фундамент или вбить опорные сваи под каждый угол основы (форма фигуры повторяет очертания нижнего ряда схемы – десяти-, восьми- или двенадцатиугольник).

Высота основания зависит от того, как предполагается использовать постройку – для легкого летнего парника хватит 15-20 см, а для зимней теплицы с теплыми грядками лучше поднять стенки на 50-70 см. Основу обычно изготавливают из толстого бруса или деревянных щитов. Невысокое временное сооружение можно установить прямо на кирпичи или камни, уложенные под углы нижнего ряда каркаса.

Сборка и обшивка каркаса

Конструкцию собирать лучше снизу-вверх, соединяя ребра коннекторами или шурупами в соответствии со схемой. Вершину купола удобнее собрать на земле, и только потом прикрепить к каркасу. Заниматься монтажом такого «конструктора для взрослых» лучше с помощником – так удобнее фиксировать детали. Для входа во время сборки вместо нескольких элементов купола вставляется дверная коробка.

Совет! Для вентиляции установите в верхней части купола 2 рамки-форточки, изготовленные по внутренним размерам треугольного элемента.

Следующий этап – обшивка каркаса. Для этих работ выбирается плотный прозрачный материал – парниковая пленка, поликарбонат или стекло. Существует несколько способов укрыть купольную теплицу:

• готовый каркас обтягивают пленкой поверху;
• вырезают треугольники из поликарбоната (по размеру каждой ячейки каркаса) и крепятся, как мозаика;
• в ячейки каркаса вставляют стекло.

После того как купол полностью обшит, нужно проверить его герметичность. При необходимости места соединения реек и обшивки дополнительно герметизируют.

Видео:ГудКарма - принцип сборки купольного каркаса, особенности монтажа | Айсдом.рфСкачать

Внутреннее обустройство геотеплицы

Сборка геокупола своими руками завершена, самое время обустроить его внутри. До закладывания грядок необходимо подготовить системы обогрева, полива и вентиляции. Внутри купола по северной стороне необходимо закрепить блестящий материал (фольгу, металлизированную пленку) – так растения и резервуары с водой получат больше света и тепла.

Температура в теплице поддерживается с помощью самодельных аккумуляторов тепла – под светоотражающим щитом устанавливают несколько бочек с водой. Вода за день нагреется, благодаря чему ночью внутри будет поддерживаться необходимая температура. Эту же воду можно использовать для капельного полива.

Для обогрева грядок под слоем почвы можно уложить гофрированные трубы, в которые будет подаваться теплый воздух.

Трубы засыпают слоем навоза или компоста. Теплый воздух циркулирует по системе под грядками благодаря вентилятору, подключенному к солнечной батарее. Дополнительно для аккумуляции тепла в центре теплицы можно установить несколько пятилитровых фляг, также заполненных водой. Кроме встроенных форточек, можно установить автоматическую систему вентиляции для проветривания по расписанию.

Грядки в купольной теплице располагают по периметру.

Ширину грядки лучше делать не больше, чем 1,5 м, иначе тяжело ухаживать за растениями. Какую именно грядку обустроить – дело вкуса. Можно построить стандартные – до 40 см в высоту, высокие или теплые, вертикальные или двухъярусные. При большом радиусе основания в центре обычно обустраивают грядку-клумбу, на которой высаживают высокорослые или вьющиеся культуры.

Геодезические теплицы на природном обогреве подходят для выращивания любых культур в период с ранней весны и до ноября. При достаточно большом объеме купола и наличии дополнительного отопления и подсветки такие теплицы пригодны для круглогодичного использования даже в районах с умеренным климатом.

Как видите, самостоятельно построить на участке оригинальную теплицу-купол несложно. И если учесть, что затраты на ее создание и содержание несколько меньше, чем для других укрытий, то можно смело сказать, что популярность таких сооружений будет расти с каждым годом.

Видео:Геодезический купол.Скачать

Построение модели геодезического купола

Построение модели геодезического купола — Гуманитарные Науки

Видео:Как сделать геокупол? | Геодезический купол своими рукамиСкачать

Содержание:

Геодезические купола — эффективный способ сделать здания. Они недороги, прочны, просты в сборке и легко ломаются. После того, как купола построены, их можно даже взять и перенести в другое место. Купола делают хорошие временные аварийные укрытия, а также долговременные здания. Возможно, когда-нибудь они будут использованы в космическом пространстве, на других планетах или под океаном. Знать, как они собраны, не только практично, но и весело

Если бы геодезические купола были сделаны, как автомобили и самолеты, на сборочных линиях в большом количестве, почти каждый в мире сегодня мог бы позволить себе иметь дом. Первый современный геодезический купол был спроектирован немецким инженером доктором Вальтером Бауэрсфельдом в 1922 году для использования в качестве проекционного планетария. В Соединенных Штатах изобретатель Бакминстер Фуллер получил свой первый патент на геодезический купол (патент № 2 682 235) в 1954 году.

Приглашенный писатель Тревор Блейк, автор книги «Библиография Бакминстера Фуллера» и архивариус крупнейшей частной коллекции произведений Р. Бакминстера Фуллера и о нем, собрал наглядные пособия и инструкции для создания недорогой, простой в сборке модели один тип геодезического купола. Если вы не будете осторожны, вы также можете узнать о корне геодезии — «геодезии».

Посетите веб-сайт Тревора по адресу synchronofile.com.

Видео:#2 Расчет купольных домов сферические теплицы Geodesic dome calculatorСкачать

Будьте готовы построить модель геодезического купола

Прежде чем мы начнем, полезно понять некоторые концепции, лежащие в основе строительства купола. Геодезические купола не обязательно построены как великие купола в истории архитектуры. Геодезические купола обычно представляют собой полусферы (части сфер, как половина шара), состоящие из треугольников. Треугольники состоят из трех частей:

• лицо — часть посередине
• край — линия между углами
• вершина — где встречаются ребра

Все треугольники имеют две грани (одна видна изнутри купола, другая — снаружи), три ребра и три вершины. В определении угла вершина — это угол, где встречаются два луча.

Может быть много разных длин по краям и углам вершины в треугольнике. Все плоские треугольники имеют вершину, которая составляет до 180 градусов. Треугольники, нарисованные на сферах или других формах, не имеют вершин, составляющих до 180 градусов, но все треугольники в этой модели плоские.

Если вы не ходили в школу слишком долго, вы можете освежиться в типах треугольников. Один вид треугольника представляет собой равносторонний треугольник, который имеет три ребра одинаковой длины и три вершины одинакового угла. В геодезическом куполе нет равносторонних треугольников, хотя различия по краям и вершине не всегда видны сразу.

Выполняя шаги по созданию этой модели, сделайте все треугольные панели, как описано, с плотной бумагой или прозрачной пленкой, затем соедините панели с помощью бумажных крепежных элементов или клея.

Видео:Каркас геокуполов для глэмпинга и мероприятий. Основа конструктива сферы. Распаковка купола ЗСКСкачать

Шаг 1: сделать треугольники

Первым шагом в создании вашей геометрической модели купола является вырезание треугольников из плотной бумаги или прозрачных пленок. Вам понадобятся два разных типа треугольников. Каждый треугольник будет иметь одно или несколько ребер, измеренных следующим образом:

Край A = .3486
Край B = .4035
Край С = .4124

Перечисленные выше длины кромок могут быть измерены любым способом (включая дюймы или сантиметры). Важно сохранить их отношения. Например, если вы делаете ребро А длиной 34,86 сантиметра, то делайте ребро Б длиной 40,35 сантиметра, а ребро С 41,24 сантиметра.

Сделайте 75 треугольников с двумя C-ребрами и одним B-ребром. Они будут называться Панели CCB, потому что у них есть два ребра C и один ребро B.

Сделайте 30 треугольников с двумя ребрами A и одним ребром B.

Включите складной клапан на каждом краю, чтобы вы могли соединить свои треугольники с помощью бумажных застежек или клея. Они будут называться Панели AAB, потому что у них есть два ребра A и один ребро B.

Теперь у вас есть 75 панелей CCB и 30 панелей AAB.

Видео:Сравнение прочности купола из треугольников и из трапеций!Скачать

Рассуждение

Этот купол имеет радиус один. То есть, чтобы сделать купол, в котором расстояние от центра до внешней стороны равно единице (один метр, одна миля и т. Д.), Вы будете использовать панели, которые делятся на единицу на эти величины. Итак, если вы знаете, что вам нужен купол диаметром один, вы знаете, что вам нужна стойка A, которая разделена на 0,348.

Вы также можете сделать треугольники по их углам. Вам нужно измерить угол АА, который точно равен 60.708416 градусам? Не для этой модели, потому что измерения до двух десятичных знаков должно быть достаточно. Здесь представлен полный угол, чтобы показать, что каждая из трех вершин панелей AAB и трех вершин панелей CCB складывается на 180 градусов.

_{AA = 60,708416
AB = 58,583164
CC = 60.708416
CB = 58,583164}

Видео:сборка геодезического купола за 4 часаСкачать

Шаг 2: Сделайте 10 шестиугольников и 5 полугексагонов

Соедините края C шести панелей CCB, чтобы сформировать шестиугольник (шестиугольная форма). Наружный край шестиугольника должен быть всеми краями B.

Сделайте десять шестиугольников из шести панелей CCB. Если вы присмотритесь, вы сможете увидеть, что шестиугольники не плоские. Они образуют очень неглубокий купол.

Остались ли какие-то панели CCB? Хорошо! Тебе это тоже нужно.

Сделайте пять полугексагонов из трех панелей CCB.

Видео:Только не купольный! 6 лет спустя владельцы такого объекта решили строить другой дом // FORUMHOUSEСкачать

Шаг 3: сделайте 6 пятиугольников

Соедините края A пяти панелей AAB, чтобы сформировать пятиугольник (пятигранную форму). Внешний край пятиугольника должен быть всеми краями B.

Сделайте шесть пятиугольников из пяти панелей AAB. Пентагоны также образуют очень неглубокий купол.

Видео:Глюоны: самые странные частицы в квантовой физикеСкачать

Шаг 4: Соедините шестиугольники с Пентагоном

Этот геодезический купол построен сверху вниз. Один из пятиугольников, сделанных из панелей AAB, станет самым верхним.

Возьмите один из пятиугольников и соедините с ним пять шестиугольников. Ребра B пятиугольника имеют ту же длину, что и ребра B шестиугольников, поэтому они и соединяются.

Теперь вы должны увидеть, что очень мелкие купола шестиугольников и пятиугольника образуют менее мелкий купол, если их соединить. Ваша модель уже начинает выглядеть как «настоящий» купол, но помните — купол — это не шар.

Видео:Купольный дом своими руками. Часть 1. БезконнекторныйСкачать

Шаг 5: Соедините пять пятиугольников с шестиугольниками

Возьмите пять пятиугольников и соедините их с внешними краями шестиугольников. Как и прежде, B-ребра — это те, которые нужно соединить.

Видео:Построили тёплый купольный дом. Пошаговый процесс строительстваСкачать

Шаг 6: подключи еще 6 шестиугольников

Возьмите шесть шестиугольников и соедините их с внешними краями B пятиугольников и шестиугольников.

Видео:Последний треугольник в каркас купола ГудКармаСкачать

Шаг 7: соединяем полугексагоны

Наконец, возьмите пять полугексагонов, которые вы сделали в Шаге 2, и соедините их с внешними краями шестиугольников.

Поздравляем! Вы построили геодезический купол! Этот купол представляет собой 5/8 сферы (шара) и представляет собой трехчастотный геодезический купол. Частота купола измеряется количеством ребер от центра одного пятиугольника до центра другого пятиугольника. Увеличение частоты геодезического купола увеличивает сферический (шарообразный) купол.

Если вы хотите сделать этот купол с распорками вместо панелей, используйте те же соотношения длины, чтобы сделать распорки 30 A, 55 B и 80 C.

Теперь вы можете украсить свой купол. Как бы это выглядело, если бы это был дом? Как бы это выглядело, если бы это была фабрика? Как бы это выглядело под океаном или на луне? Куда пойдут двери? Куда пойдут окна? Как бы свет засиял внутри, если бы вы построили купол сверху?

Хотели бы вы жить в доме с геодезическим куполом?

Видео:Как построить геодезический купол в ArchiCADСкачать

Геодезический купол. Об устройстве и моем опыте расчетов

Пожалуй сложно назвать геодезические купола чем-то необычным или новым. В этой заметке я расскажу немного об этих конструкциях в общем, об их устройстве, а также покажу на примере как я кое что на эту тему считал. Код тоже будет.

Википедию цитировать не буду. Почему я выбрал купол в качестве дома?

• При равном объеме площадь поверхности сферы будет меньше, чем у любой другой формы. Это положительно влияет как на материалоемкость, так и на энергозатраты при эксплуатации.
• Мне нравится как выглядит сфера.
• Это интересный инженерный проект, в каком-то смысле даже вызов. Это сложно, трудно и потому весело!

Как это геодезические сферы устроены вообще? С первого взгляда кажется, что это какое-то переплетение рёбер и уловить систему сложно. В этой заметке попробуем разобраться.

В основе таких конструкций лежит икосаэдр или октаэдр. В общем правильный многогранник.
В моем случае это был именно икосаэдр и чаще используют его. Далее берем одну грань и заменяем ее на несколько треугольников, вершины которых лежат на сфере, центр которой совпадает с центром икосаэдра. Звучит не слишком складно. Отвлечемся.

Есть замечательный калькулятор www.acidome.ru который позволяет в реальном времени покрутить геодезик. Берем в качестве основы icosahedron, ставим частоту 1, часть сферы 1/1.

Это и есть наш основной икосаэдр. Частота это на сколько частей мы разобьем каждое ребро икосаэдра. Ставим 3,4, 5 и ничего становится непонятно. Переключаем в режим кровли и ищем пятиугольники. В тех местах, где у нас вершина икосаэдра — будет пятиугольник. Между тремя пятиугольниками грань икосаэдра.

Если внимательно смотреть на геодезик и знать, что искать (обычно пятиугольник), то становится видна регулярность структуры. На Биосфере в Монреале при должном усердии можно найти пятиугольники и посчитать частоту. Частота у нас равна количеству ребер между двумя пятиугольниками.

Сами “большие” треугольники, с вершинами на вершинах икосаэдра также имеют структуру. На acidome в режиме кровли это видно по цвету. Треугольники расположены симметрично относительно центра “большого” треугольника. Количество их типов меньше общего числа треугольников. В случае с частотой 5 уникальных треугольников 9.

В процессе проектирования дома я столкнулся с задачей постройки сферы в Dynamo. Это такой инструмент, который позволяет научить Autodesk Revit работать со сложными формами. Такая среда визуального программирования.
Погуглив я даже нашел скетч, который в Dynamo строил геодезическую сферу. Сферу то он строил, да не ту.

Дело вот в чем. Когда мы берем одно ребро икосаэдра и делим его на мелкие треугольники — сделать это можно несколькими способами. В acidome за это отвечает переключатель “метод разбиения”.

Найденный скетч строил сферу методом равных хорд. Что это значит? Мы берем большой треугольник икосаэдра, каждое его ребро делим на нужное нам количество частей, соединяем точки на ребрах между собой и получаем плоскую сетку из треугольников. Затем эту сетку мы проецируем на сферу. Все бы хорошо, но сами эти треугольники достаточно сильно отличаются по размеру. Центральный больше всех. Оно и понятно, центр “большого” треугольника у нас на максимальном расстоянии от сферы. Это плохо, так как в этом случае сложнее оптимизировать расход материалов. Будет больше отходов.

Другой метод разбиения (равными дугами) предполагает, что мы строим поверх “большого” треугольника дуги и уже их делим на равные части. Подход отличается, простой проекцией не обойтись.

Скетч не подходил. Я попытался его исправить и в итоге мне пришлось нырнуть в это дело с головой.

Как оказалось помимо визуальной среды Dynamo имеет встроенный Python. С этим языком я ранее не сталкивался, но где наша не пропадала? В конце концов это просто инструмент.

Дальше будут кусочки кода, прошу обратить внимание, что это мой hello world в python, а целью было не построить максимально эффективное и производительное решение, а построить нужную сферу.

Метод равных дуг.

Берем одну из граней икосаэдра и из углов этого треугольника строим дуги.

Затем дуги делим на равные части и соединяем точки на дугах новыми дугами. У всех дуг один центр — центр сферы. Точки соединяем не все со всеми, а одноименные. На картинке оно выглядит попроще, чем в коде.

Опа, а дуги то не пересекаются! Не слишком беглое гугление вывело меня на книгу, которая подтвердила мои предположения о том, что нужно в качестве вершины ребра геодезика использовать центр треугольника, образованного пересечением дуг. Также курил исходники acidome, но не помню нашел ли там этому подтверждение. Помню, что было интересно.
Центры надо как-то найти. Это центр треугольника и это не сложно, но нужно было понять где же у нас в ворохе точек эти треугольники. Мне показалось самым простым вариантом соединять ближайшие друг к другу точки.

Теперь нам нужно соединить между собой собранные на разных этапах точки, которые и являются вершинами ребер геодезической сферы. На картинке эти точки видно хорошо, но вот когда они в массиве — все сложнее. Было несколько вариантов, но так как задача была с наименьшими трудозатратами получить рабочий скрипт, вышло вот это:

Сегмент готов. Наверное существует какой-то правильный путь для решения этой задачи, но я проложил свой.

Дальше сегмент разворачивается, несколько раз копируется копируется и получается полная сфера. Вот один из поворотов:

Скриптик вышел страшненький, я его пару раз переписывал, так как были проблемы с экспортом в Revit. Думал, что проблемы с построением. В итоге на форуме Dynamo индус подсказал украинцу и все удалось!

Теперь можно строить сферу любой частоты и любого диаметра. Сравнение размеров с результатами acidome показало, что все сходится с высокой точностью. Повторяемость это хорошо.

Также я занялся оптимизацией размеров с целью минимизации обрезков. Так как все размеры были у меня на руках это было не так трудно. В итоге радиус сферы получился 5,65 метров при частоте 5. Такие размеры позволяют мне достаточно эффективно использовать материалы шириной 125 см. Такую ширину имеют листы OSB, листового металла, утеплителя, гипсокартона. При хорошей оптимизации количество обрезков минимально. Наилучших результатов можно добиться путем расчета раскладок треугольников на материале, но этим я не занимался.

Дальше было проще, так как Revit съел сложную форму и позволил с ней работать примерно с тем же успехом, что и с квадратно-параллельной.

Конечно, трудности на этом не закончились, но это уже совсем другая история.

💥 Видео

КУПОЛЬНЫЙ ДОМ | ХУДШИЙ КАРКАСНИК НА СВЕТЕ | СТРОЙХЛАМСкачать

Каркас геодезического купола в разобранном виде.Скачать

Вторая версия как сделать крышку, купол на уличный бассейн.Скачать

Как построить дом купол. Геодезический купол. Glamping. How to build geodesic dome?Скачать

геодезический купол сборкаСкачать