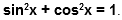Где на окружности находится п 12

Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.

Видео:Как искать точки на тригонометрической окружности.Скачать

Обозначаем числа (2π), (π), (frac), (-frac), (frac)

Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.

Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.

Отметим точку (frac) . (frac) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.

Обозначим на окружности точки (-) (frac) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число (frac) . Для этого дробь (frac) переведем в смешанный вид (frac) (=1) (frac) , т.е. (frac) (=π+) (frac) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac) .

Видео:Деление окружности на 12 равных частейСкачать

Обозначаем числа (frac), (frac), (frac)

Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac) , (frac) и (frac) .
(frac) – это половина от (frac) (то есть, (frac) (=) (frac) (:2)) , поэтому расстояние (frac) – это половина четверти окружности.

(frac) – это треть от (π) (иначе говоря, (frac) (=π:3)), поэтому расстояние (frac) – это треть от полукруга.

(frac) – это половина (frac) (ведь (frac) (=) (frac) (:2)) поэтому расстояние (frac) – это половина от расстояния (frac) .

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением (0), (frac) ,(π), (frac) , (frac) , (frac) , (frac) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.

Разные расстояние на окружности наглядно:

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Обозначаем числа (frac), (-frac), (frac)

Обозначим на окружности точку (frac) , для этого выполним следующие преобразования: (frac) (=) (frac) (=) (frac) (+) (frac) (=π+) (frac) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac) .

Отметим на окружности точку (-) (frac) . Преобразовываем: (-) (frac) (=-) (frac) (-) (frac) (=-π-) (frac) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac) .

Нанесем точку (frac) , для этого преобразуем (frac) (=) (frac) (=) (frac) (-) (frac) (=2π-) (frac) . Значит, чтобы поставить точку со значением (frac) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac) .

Видео:Длина окружности. Математика 6 класс.Скачать

Обозначаем числа (10π), (-3π), (frac) ,(frac), (-frac), (-frac)

Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.

Из этого примера можно сделать вывод:

Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.

То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».

Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).

Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).

Кстати, там же будут находиться все нечетные (π).

Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).

Сейчас обозначим число (frac) . Как обычно, преобразовываем: (frac) (=) (frac) (+) (frac) (=3π+) (frac) (=2π+π+) (frac) . Два пи – отбрасываем, и получается что, для обозначения числа (frac) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac) (т.е. половину окружности и еще четверть).

Отметим (frac) . Вновь преобразования: (frac) (=) (frac) (=) (frac) (+) (frac) (=5π+) (frac) (=4π+π+) (frac) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac) – и мы найдем место точки (frac) .

Нанесем на окружность число (-) (frac) .
(-) (frac) (= -) (frac) (-) (frac) (=-10π-) (frac) . Значит, место (-) (frac) совпадает с местом числа (-) (frac) .

Обозначим (-) (frac) .
(-) (frac) (=-) (frac) (+) (frac) (=-5π+) (frac) (=-4π-π+) (frac) . Для обозначение (-) (frac) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac) .

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Где на окружности пи 12

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Как обозначать числа с пи на числовой окружности?

Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.

Видео:Отбор корней по окружностиСкачать

Обозначаем числа (2π), (π), (frac ), (-frac ), (frac )

Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.

Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.

Отметим точку (frac ) . (frac ) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.

Обозначим на окружности точки (-) (frac ) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число (frac ) . Для этого дробь (frac ) переведем в смешанный вид (frac ) (=1) (frac ) , т.е. (frac ) (=π+) (frac ) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac ) .

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Обозначаем числа (frac ), (frac ), (frac )

Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac ) , (frac ) и (frac ) .
(frac ) – это половина от (frac ) (то есть, (frac ) (=) (frac ) (:2)) , поэтому расстояние (frac ) – это половина четверти окружности.

(frac ) – это треть от (π) (иначе говоря, (frac ) (=π:3)), поэтому расстояние (frac ) – это треть от полукруга.

(frac ) – это половина (frac ) (ведь (frac ) (=) (frac ) (:2)) поэтому расстояние (frac ) – это половина от расстояния (frac ) .

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением (0), (frac ) ,(π), (frac ) , (frac ) , (frac ) , (frac ) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.

Разные расстояние на окружности наглядно:

Видео:Радиус и диаметрСкачать

Обозначаем числа (frac ), (-frac ), (frac )

Обозначим на окружности точку (frac ) , для этого выполним следующие преобразования: (frac ) (=) (frac ) (=) (frac ) (+) (frac ) (=π+) (frac ) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac ) .

Отметим на окружности точку (-) (frac ) . Преобразовываем: (-) (frac ) (=-) (frac ) (-) (frac ) (=-π-) (frac ) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac ) .

Нанесем точку (frac ) , для этого преобразуем (frac ) (=) (frac ) (=) (frac ) (-) (frac ) (=2π-) (frac ) . Значит, чтобы поставить точку со значением (frac ) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac ) .

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Обозначаем числа (10π), (-3π), (frac ) ,(frac ), (-frac ), (-frac )

Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.

Из этого примера можно сделать вывод:

Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.

То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».

Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).

Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).

Кстати, там же будут находиться все нечетные (π).

Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).

Сейчас обозначим число (frac ) . Как обычно, преобразовываем: (frac ) (=) (frac ) (+) (frac ) (=3π+) (frac ) (=2π+π+) (frac ) . Два пи – отбрасываем, и получается что, для обозначения числа (frac ) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac ) (т.е. половину окружности и еще четверть).

Отметим (frac ) . Вновь преобразования: (frac ) (=) (frac ) (=) (frac ) (+) (frac ) (=5π+) (frac ) (=4π+π+) (frac ) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac ) – и мы найдем место точки (frac ) .

Нанесем на окружность число (-) (frac ) .
(-) (frac ) (= -) (frac ) (-) (frac ) (=-10π-) (frac ) . Значит, место (-) (frac ) совпадает с местом числа (-) (frac ) .

Обозначим (-) (frac ) .
(-) (frac ) (=-) (frac ) (+) (frac ) (=-5π+) (frac ) (=-4π-π+) (frac ) . Для обозначение (-) (frac ) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac ) .

Видео:КАК РАЗДЕЛИТЬ ОКРУЖНОСТЬ НА 12 РАВНЫХ ЧАСТЕЙ?Скачать

Точка пи / 12 где находиться на тригонометрической окружности?

Математика | 10 — 11 классы

Точка пи / 12 где находиться на тригонометрической окружности.

π / 12 = 180 / 12 = 15°

пояснение на картинке.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Диаметр окружности равен 12 см?

Диаметр окружности равен 12 см.

Какое расстояние может быть от центра этой окружности до точки, чтобы эта точка находилась внутри окружности?

Видео:Тригонометрическая окружность. Как выучить?Скачать

Число 3п соответствует точке тригонометрической окружности с ординатой ?

Число 3п соответствует точке тригонометрической окружности с ординатой ?

Видео:Длина окружности и площадь круга. Урок 12. Геометрия 9 классСкачать

Начертите окружность с центром в точке О и радиусом 3 см 5 мм?

Начертите окружность с центром в точке О и радиусом 3 см 5 мм.

Проведите прямую, которая пересекает окружность в точках М и К.

На каком расстояние от центра окружности находятся эти точки?

Видео:Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать

Начерти окружность с центром О и радиус 3 см 5 мм?

Начерти окружность с центром О и радиус 3 см 5 мм.

Проведите прямую, которая пересекает окружность в точках М и К, На каком расстоянии от центра окружности находятся эти точки?

Видео:Вычисление значений тригонометрических функцийСкачать

Отметь красным цветом точки которые находятся на окружности с центром в точке О?

Отметь красным цветом точки которые находятся на окружности с центром в точке О.

Видео:Выборка с помощью окружностиСкачать

Подскажите где на окружности находятся точки [0 ; 2pi]?

Подскажите где на окружности находятся точки [0 ; 2pi].

Видео:Как решить пункт б) в задании 13 профиля ЕГЭ. ТригонометрияСкачать

Вася сказал, что окружность это геометрическая фигура все точки которой находятся на одинаковом расстоянии от данной точки, а Валя сказала что такая фигура — не обязательно окружность?

Вася сказал, что окружность это геометрическая фигура все точки которой находятся на одинаковом расстоянии от данной точки, а Валя сказала что такая фигура — не обязательно окружность.

Кто из них прав?

Видео:+Как найти длину окружностиСкачать

Где находится на числовой окружности точка — пи / 12?

Где находится на числовой окружности точка — пи / 12.

Видео:Как разделить окружность на 12 частей How to divide a circle into 12 partsСкачать

Отметьте в тетради точку о?

Отметьте в тетради точку о.

Постройте окружность с центром в этой точке.

Измерь радиус окружности.

Чему равен диаметр.

Объясните пожалусто как диаметр находить))).

Нарисуй две окружности радиусом 3 см, чтобы они пересекались?

Нарисуй две окружности радиусом 3 см, чтобы они пересекались.

Отметь точки, которые принадлежат обеим окружностям.

Отметь точку, которая находится внутри обеих окружностей.

Сколько таких точек?

На этой странице сайта размещен вопрос Точка пи / 12 где находиться на тригонометрической окружности? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

56•60 = 3360 секунд 56 я умножаю на 60 секунд вот тебе ответ 3360.

(1 00 + 80 : 5) : 2 = 58 ((100 — 80) * 5) : 2 = 50.

Делители числа 12 это числа : 12, 6, 4, 3, 2, 1. Эти точки и нужно изобразить на координатном луче.

Единичная окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Единичная окружность в тригонометрии

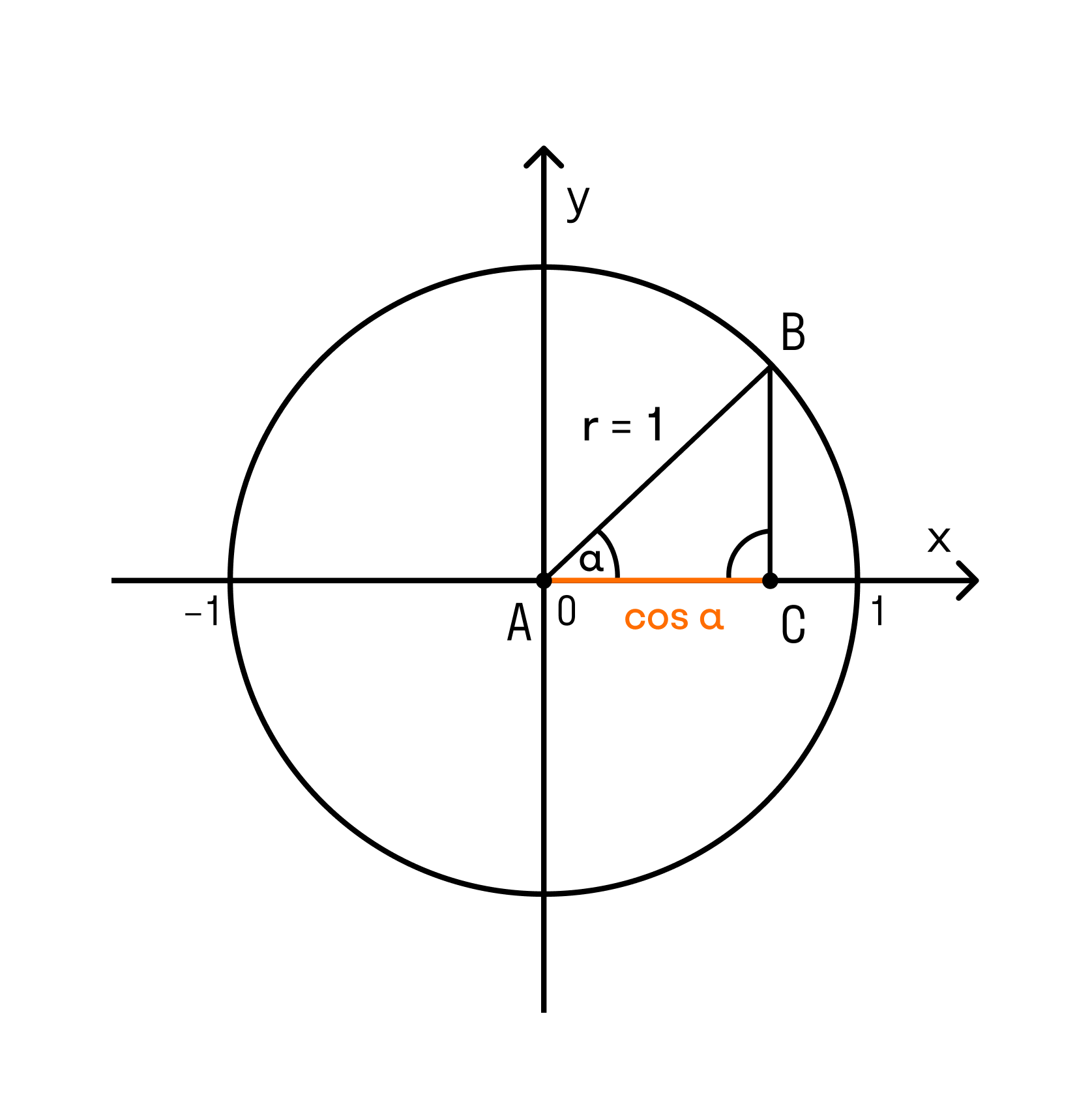
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

• Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
• Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
• В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
• В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

• 2π радиан = 360°
• 1 радиан = (360/2π) градусов
• 1 радиан = (180/π) градусов
• 360° = 2π радиан
• 1° = (2π/360) радиан
• 1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Где находится на числовой окружности точка — пи / 12?

Математика | 10 — 11 классы

Где находится на числовой окружности точка — пи / 12.

Находится в IV четверти.

Если нужно в градусы, чтоб легче определить было, то — π / 12 * 180° / π = — 15°.

Диаметр окружности равен 12 см?

Диаметр окружности равен 12 см.

Какое расстояние может быть от центра этой окружности до точки, чтобы эта точка находилась внутри окружности?

Найдите все числа, которым соотвествуют отмеченные на числовой окружности точки?

Найдите все числа, которым соотвествуют отмеченные на числовой окружности точки.

Обозначьте на числовой окружности точку, которая соответствует данному числу : 3пи?

Обозначьте на числовой окружности точку, которая соответствует данному числу : 3пи.

На числовой окружности отмечена точка соответствующая числу минус 35 пи деленное на 4?

На числовой окружности отмечена точка соответствующая числу минус 35 пи деленное на 4.

Начертите окружность с центром в точке О и радиусом 3 см 5 мм?

Начертите окружность с центром в точке О и радиусом 3 см 5 мм.

Проведите прямую, которая пересекает окружность в точках М и К.

На каком расстояние от центра окружности находятся эти точки?

Отметь красным цветом точки которые находятся на окружности с центром в точке О?

Отметь красным цветом точки которые находятся на окружности с центром в точке О.

Подскажите где на окружности находятся точки [0 ; 2pi]?

Подскажите где на окружности находятся точки [0 ; 2pi].

Найдите на числовой окружности точку, которая соответствует заданному числу : 7П / 2 ; — 3П / 2 ; 9П?

Найдите на числовой окружности точку, которая соответствует заданному числу : 7П / 2 ; — 3П / 2 ; 9П.

Отметьте в тетради точку о?

Отметьте в тетради точку о.

Постройте окружность с центром в этой точке.

Измерь радиус окружности.

Чему равен диаметр.

Объясните пожалусто как диаметр находить))).

Точка пи / 12 где находиться на тригонометрической окружности?

Точка пи / 12 где находиться на тригонометрической окружности.

На этой странице находится ответ на вопрос Где находится на числовой окружности точка — пи / 12?, из категории Математика, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.