Где используется деление окружности на части

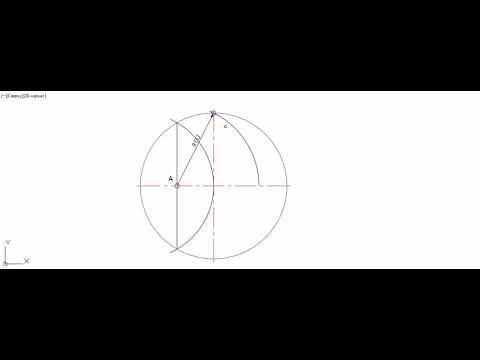
Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.

Термины при построениях окружности

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.

Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.

Части окружностей называются дугами.

Прямая СD, соединяющая две точки на окружности, называется хордой.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.

Часть круга, ограниченная хордой СD и дугой, называется сигментом.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.

Угол, образованный двумя радиусами КОА, называется центральным углом.

Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на 4 и 8 одинаковых частей

Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

Видео:Деление окружности на 12 равных частейСкачать

Деление окружности на 3 и 6 равных частей (кратные 3 трём)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.

Видео:1 2 2 деление окружности на 5 равных частейСкачать

Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.

Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.

Видео:Деление окружности на 6 равных частейСкачать

Нахождение центра дуги окружности

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.

Видео:Деление окружности на n- равные частиСкачать

Интегрированный урок (черчение + геометрия) «Деление окружности на равные части»

Разделы: Математика

Цель: Показать учащимся необходимость применения геометрических построений при выполнении чертежей детали. Дать знания по теме «Деление окружности на равные части.

Задачи:

• Научить делить окружность на равные части.
• Развивать наблюдательность, умение мыслить логически.
• Воспитывать внимательность и аккуратность в выполнении чертежей.

Тип урока: Урок изучения нового материала

Методы проведения: беседа, графические построения, рассказ с демонстрацией, упражнения.

Оборудование для учителя: Модели технических деталей, иллюстрации примеров применения геометрических построений (диск CD-RW), ПК, шаблоны и карточки – задания.

Оборудование для учащихся: Учебник, тетрадь, чертёжные инструменты.

План урока

1. Организационная часть (3 м.)
2. Объяснение нового материала (18м.)
3. Закрепление изученного материала (12м.)
4. Подведение итогов (5м.)
5. Домашнее задание (2м.)

Видео:1 2 3 деление окружности на 7 равных частейСкачать

Ход урока

1. Организационная часть

Проверить готовность к уроку. Сегодня будем изучать тему «Деление окружности на равные части». Моя задача научить вас делить окружность на равные части.

Объяснение нового материала (18м.)

2. Объяснение нового материала

Вступительная беседа (5 мин).

Вопрос: Скажите, где вы встречались с геометрическими построениями? Приведите примеры из жизни, техники применения деления отрезков, углов, окружностей на равные части. (Мнения учащихся.)

Почему важна эта тема? Для построения правильных многоугольников, которые вы будете изучать в 9 классе. Вы должны научиться делить окружности на равные части.

А сейчас из истории немного узнаем, нам расскажут об этом ребята.

1 ученик. Приемы деления окружности на равные части человек использовал с незапамятных времен. Например, превращение колеса из сплошного диска в обод со спицами поставило человека перед необходимостью распределить спицы в колесе равномерно. Выполняя изображение такого колеса, люди искали точные способы с помощью чертежных инструментов.

С делением окружности неразрывно связано построение правильных многоугольников. Они встречаются в древнейших орнаментах у всех народов. Люди уже тогда оценили их красоту. Кроме того, они видели эти фигуры в природе. Например, пятиугольник встречается в очертаниях минералов, цветов, плодов, в форме некоторых морских животных, шестиугольник просматривается в пчелиных сотах и т. п. (Показ иллюстраций — см. рис. 2.)

2 ученик. В строительстве широко применяли деления окружности на равные части. Одним из примеров может служить величественный памятник готической архитектуры Нотр-Дам де Пари или Собор Парижской Богоматери (130 метров в длину, 108 — в ширину), который находится в Париже, на острове Сите. Его строили 94 года. Фасад Собора украшает удивительный витраж XIII века. Этот витраж в архитектуре называется «роза». Диаметр розы собора Парижской Богоматери 12 метров 90 см. (Показ иллюстраций — см. рис. 4.)

Рис 2

рис 4

3 ученик. В декоративно-прикладном искусстве дизайнеры, ювелиры с успехом применяли деление окружности, создавая прекрасные произведения: ордена, медали, монеты, ювелирные изделия. (Показ иллюстраций.)

Посмотрите внимательно на вещи, окружающие вас, несомненно, вы найдете еще очень много примеров использования темы «Деление окружности».

А сейчас обратите внимание на технические детали, к примеру, различные колеса, гайки, гаечные ключи, диски, плашки, фланцы и т. д. (Показ деталей — см. рис. 5.)

При изготовлении многих типичных деталей тоже возникает необходимость в делении отрезка и окружности на равные части.

Построение окружности с деление на три равные части. (3мин.)

Я демонстрирую деталь и чертеж фланцевого соединения.

Местонахождение отверстий под болты можно найти способом деления окружности на три равные части. (Показ.)

Будем учиться данному построению (я выполняю на доске, учащиеся изучают на заготовках.)

Поставив опорную ножку циркуля в конце диаметра, опишем дугу радиусом, равным радиусу R окружности. Получим первую и вторую точки деления. Третья точка находится на противоположном конце. Итак, назовите этапы построения. (Ответы учащихся.)

Построение окружности с делением на 6 равных частей (3 мин). А сейчас — деление окружности на 6 равных частей.

Деление окружности на 4,8,16 равных частей(3 мин.)

а – на 2 части; б – на 4 части

Построение квадрата

Деление окружности на восемь равных частей

Построение восьмиугольника

Для построения чертежей некоторых деталей необходимо уметь делить окружность на равные части и строить правильные многоугольники.

Любой диаметр делит окружность на две равные части два взаимно перпендикулярных диаметра — на четыре

Центровые линии также делят окружность на четыре равные части. Соединив между собой точки пересечения центровых линий и окружности.

3. Закрепление изученного материала (12мин.)

Применим способы деления при построении чертежей

плоских деталей. Задание: Выполнение один из чертежей прокладок, приведенные на карточке, используя способы деления окружности на равные части. Нанесите размеры. Раздаю карточки.

4. Подведение итогов (3мин.)

Отметить лучших учащихся, кто работал в классе.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Где используется деление окружности на части

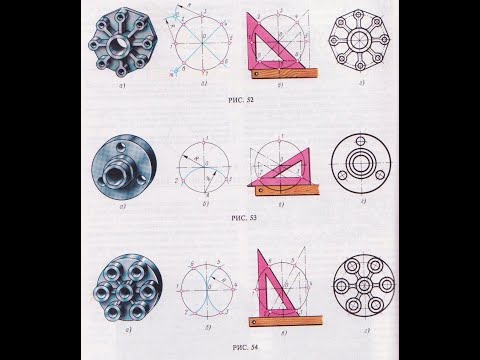
Некоторые детали машин и приборов имеют эле­менты, равномерно расположенные по окружности, например, детали на рис. 52—59. При выполнении чер­тежей подобных деталей необходимо знать правила деления окружности на равное количество частей.

Деление окружности на четыре и восемь равных частей. На рис. 52, а показана крышка, в которой име­ется восемь отверстий, равномерно расположенных по окружности. При построении чертежа контура крышки (рис. 52 г) необходимо разделить окружность на восемь равных частей. Это можно сделать с помощью угольника с углами 45° (рис. 52, в), гипоте­нуза угольника должна проходить через центр окруж­ности, или построением.

Два взаимно перпендикулярных диаметра окружно­сти делят ее на четыре равные части (точки 7, 3, 5, 7 на рис. 52, б). Чтобы разделить окружность на восемь равных частей, применяют известный прием деления прямого угла с помощью циркуля на две равные части. Получают точки 2, 4, 6, 8.

Деление окружности на три, шесть и двенадцать рав­ных частей. Во фланце (рис. 53, а) имеется три отвер­стия, равномерно расположенных по окружности. При выполнении чертежа контура фланца (рис. 53, г) нужно разделить окружность на три равные части.

Для нахождения точек, делящих окружность радиуса R на три равные части, достаточно из любой точки окружности, например точки А, провести дугу ради­усом R. Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет нахо­диться на пересечении оси окружности, проведенной из точки Л, с окружностью (рис. 53, б).

Разделить окружность на три равные части можно также угольником с углами 30 и 60° (рис. 53, в), гипотенуза угольника должна проходить через центр окруж­ности.

На рис. 54, б показано деление окружности цирку­лем на шесть равных частей. В этом случае выполня­ется то же построение, что на рис. 53, б но дугу описы­вают не один, а два раза, из точек и радиусом R , равным радиусу окружности.

Разделить окружность на шесть равных частей можно и угольником с углами 30 и 60° (рис. 54, в). На рис. 54, а показана крышка, при выполнении чертежа которой необходимо выполнить деление окружности на шесть частей.

Чтобы выполнить чертеж детали (рис. 55, а), кото­рая имеет 12 отверстий, равномерно расположенных по окружностям, нужно разделить осевую окружность на 12 равных частей (рис. 55, г).

При делении окружности на 12 равных частей с помощью циркуля можно использовать тот же прием, что и при делении окружности на шесть равных частей (рис. 54, б),но дуги радиусом R описывать четыре раза из точек 1, 7, 4и 10 (рис. 55, б).

Используя угольник с углами 30 и 60° с последующим поворотом его на 180°, делят окружность на 12 равных частей (рис. 55, в).

Деление окружности на пять, десять и семь равных частей. В плашке (рис. 56, а) имеется пять отверстий, равномерно расположенных по окружности. Выпол­няя чертеж плашки (рис. 56, в), необходимо разделить окружность на пять равных частей. Через намеченный центр О (рис. 56, б)

при помощи рейсшины и уголь­ника проводят осевые линии и из точки О циркулем описывают окружность заданного диаметра. Из точки А радиусом R, равным радиусу данной окружности, проводят дугу, которая пересечет окружность в точке n. Из точки n опускают перпендикуляр на горизон­тальную осевую линию, получают точку С. Из точки С радиусом R₁ равным расстоянию от точки С до точки 1, проводят дугу, которая пересечет горизонтальную осевую линию в точке т. Из точки 1 радиусом R , рав­ным расстоянию от точки 1 до точки m, проводят дугу, пересекающую окружность в точке 2. Дуга 12 является 1/5 длины окружности. Точки 3,4 и 5 находят, отклады­вая циркулем отрезки, равные m1.

Деталь «звездочка» (рис. 57, а) имеет 10 одинаковых элементов, равномерно расположенных по окружно­сти. Чтобы выполнить чертеж звездочки (рис. 57, я), следует окружность разделить на 10 равных частей. В этом случае следует применить то же построение, что и при делении окружности на пять частей (см. рис. 56, б). Отрезок п₁ будет равняться хорде, которая делит окружность на 10 равных частей.

На рис. 58, а изображен шкив, а на рис. 58, в — чер­теж шкива, где окружность разделена на семь равных частей.

Деление окружности на семь равных частей пока­зано на рис. 58, б. Из точки А проводится вспомога­тельная дуга радиусом R, равным радиусу данной окружности, которая пересечет окружность в точке . Из точки n опускают перпендикуляр на горизонталь­ную осевую линию. Из точки 1 радиусом, равным отрезку nс, делают по окружности семь засечек и полу­чают семь искомых точек.

Деление окружности на любое число равных частей. С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (табл. 9).

Зная, на какое число (n) следует разделить окруж­ность, находят по таблице коэффициент . При умно­жении коэффициента k на диаметр окружности D получают длину хорды l, которую циркулем отклады­вают на окружности n раз.

При построении чертежа кольца (рис. 59, а) необхо­димо окружность диаметра D=142 мм разделить на 32 равные части. Количеству частей окружности n=32 соответствует коэффициент k=0,098. Подсчитав длину хорды l=Dk=142×0,098= 13,9 мм, ее циркулем откла­дывают на окружности 32 раза (рис. 59, б и в).

💥 Видео

Деление окружности на 3 частиСкачать

Деление окружностей на равные частиСкачать

Деление окружности на 5 равных частейСкачать

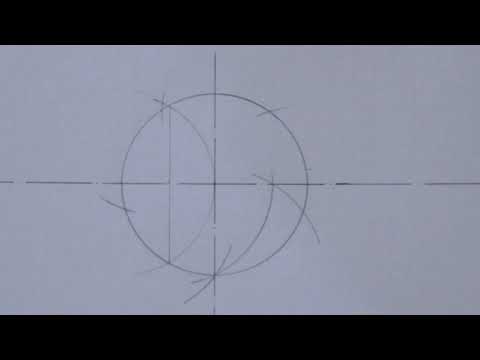
Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Как разделить окружность на 8 частей How to divide a circle into 8 partsСкачать

Деление окружности на 7 частейСкачать

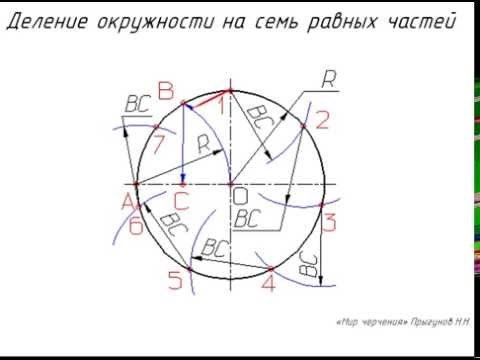
Деление окружности на равные части. Внимание!!! В таблице имеются ошибки. ПОЛЬЗУЙТЕСЬ ФОРМУЛОЙ!!!Скачать

Деление окружности на равные части с помощью циркуляСкачать

Построение шестнадцатиугольника циркулемСкачать

Красивое деление окружности на 20 частей циркулемСкачать

Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на равные частиСкачать

Деление окружности на 5 частей с помощью циркуляСкачать