Фронтально проецирующая прямая это прямая которая параллельна оси х (5 видео)

Чертежик

Содержание

Метки
Проецирующие прямые гориз-, фронт-, проф- проецир.
Проецирующие прямые
Фронтально проецирующая прямая это прямая которая параллельна оси х
🎦 Видео

Метки

Видео:Проецирование прямых частного положенияСкачать

Проецирующие прямые гориз-, фронт-, проф- проецир.

Проецирующие прямые — линии, расположенные перпендикулярно одной из плоскостей или являются параллельными направлению проецирования.

Подразделяют на следующие три вида:

1.) Горизонтально проецирующая прямая — линия перпендикулярная горизонтальной плоскости проекции(П1)

2.) Фронтально проецирующая прямая — линия перпендикулярная фронтальной плоскости проекции(П2)

3.) Профильно проецирующая прямая — линия перпендикулярная профильной плоскости проекции(П3)

Прямая общего положения

Т.е. это прямая не параллельная ни одной из плоскостей, находится под углом.

Часто студентам выдается задание на построение прямой относительно плоскости. Рассмотрим возможные варианты расположения:

Восходящая общего положения

Нисходящая общего положения

Фронтальная прямая может быть расположенная под любым углом к П1 (будь то 30 или 68 градусов)

Горизонтальная прямая может быть расположенная под любым углом к П2 (будь то 30 или 68 градусов)

Профильная прямая может быть расположенная под любым углом к П1 (будь то 30 или 68 градусов)

Видео:Проецирование прямой общего положенияСкачать

Проецирующие прямые

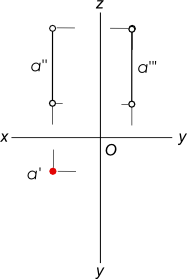
Проецирующие прямые — прямые перпендикулярные одной из плоскостей проекций. Проекцией проецирующей прямой на плоскость проекций, к которой она перпендикулярна, является точка (след прямой). Проецирующие прямые подразделяют на три вида. Горизонтально проецирующие прямые — прямые перпендикулярные горизонтальной плоскости проекции.

Такие прямые проецируются на плоскость H в точку. Их фронтальные и профильные проекции параллельны оси z. a⊥H a` — точка, a» и a»` — прямые ║ z.

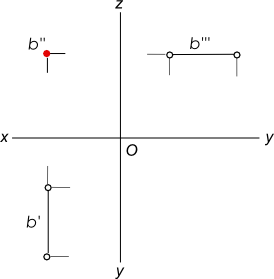
Фронтально проецирующие прямые — прямые перпендикулярные фронтальной плоскости проекции.

Эти прямые проецируются на плоскость V в точку, а их горизонтальные и профильные проекции параллельны оси y. b⊥V b» — точка, b` и b»` — прямые ║ y.

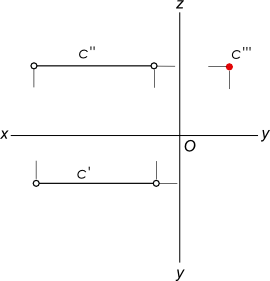
Профильно проецирующие прямые — прямые, перпендикулярные профильной плоскости проекции.

Проекциями таких прямых будут: на плоскость W — точка, на горизонтальной и фронтальной плоскостях прямые, параллельные оси x. c⊥W тогда: — c»` — точка, — c` и c» — прямые ║ x.

Видео:Лекция 1. Классификация прямых линий.Скачать

Фронтально проецирующая прямая это прямая которая параллельна оси х

Проекцией прямой, которая не перпендикулярна плоскости проекций, является прямая. Её положение определяется двумя точками, следовательно, для того чтобы построить проекцию прямой, достаточно построить проекции двух её точек.

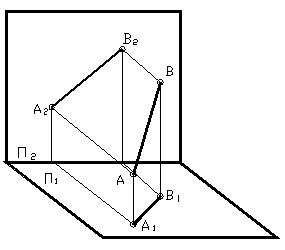
Рисунок 8

а) Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.

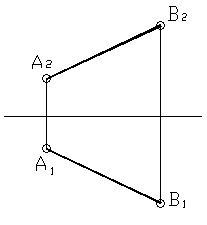
Рисунок 9

б) Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.

Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.

Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.

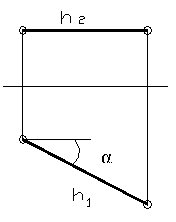
Рисунок 10

Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ð h П2.

Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.

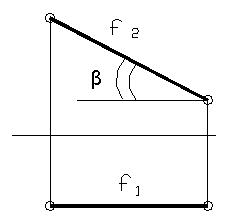
Рисунок 11

Горизонтальная проекция фронтали параллельна оси Х, а угол β — угол наклона фронтали к горизонтальной плоскости проекций; f₂ // П2, β= Ð f1 П1.

Профильная прямая – это прямая, параллельная профильной плоскости П 3 . Комплексный чертёж профильной прямой изображён на рисунке 12. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси Х, а углы α и β — соответственно, углы наклона прямой к плоскостям П 1 и П2.

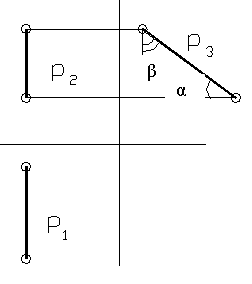
Рисунок 12.

Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.

Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.

Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).

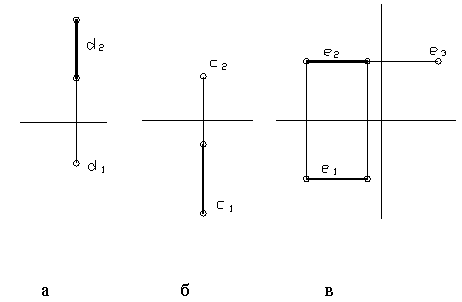
Рисунок 13

Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.

а) три точки, не лежащие на одной прямой;

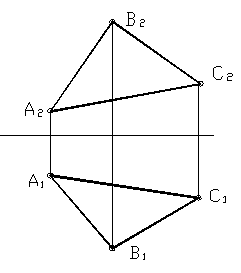
Рисунок 14

б) прямая и точка, не лежащая на ней;

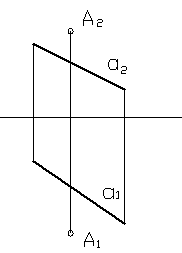
Рисунок 15

в) две параллельные прямые;

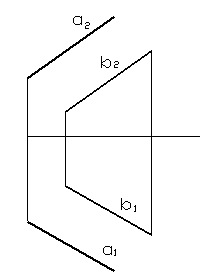
Рисунок 16

г) две пересекающиеся прямые;

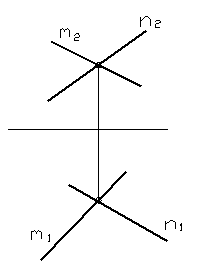
Рисунок 17

д) плоская фигура (многоугольник, круг и т.д.).

Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.

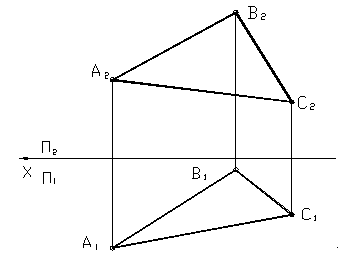
Рисунок 18

Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости – двумя пересекающимися прямыми.

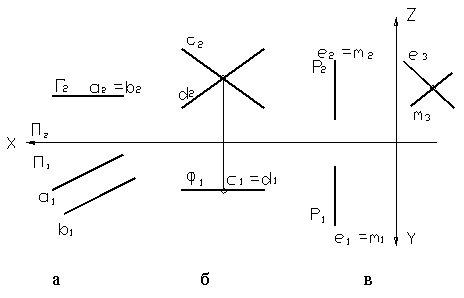
Рисунок 19

На рисунке 20 (а, б, в) показаны проецирующие плоскости. Горизонтально-проецирующая (рис. 20а) задана треугольником, фронтально-проецирующая (рис. 20б) — параллельными прямыми и профильно-проецирующая (рис. 20в) – пересекающимися прямыми.

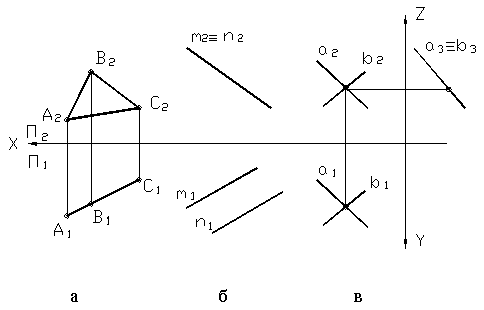
Рисунок 20