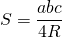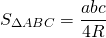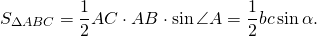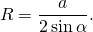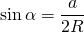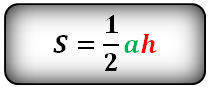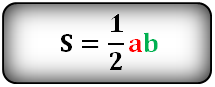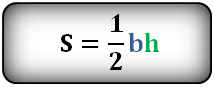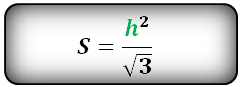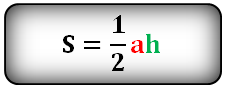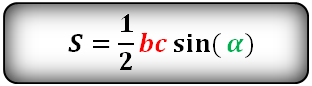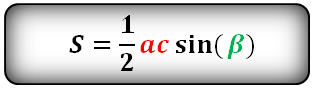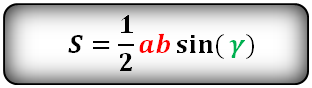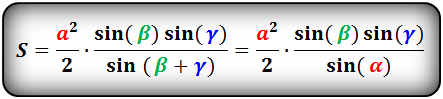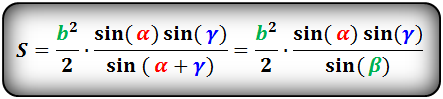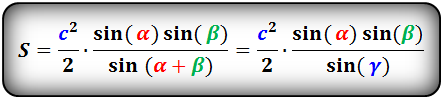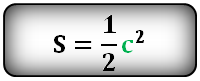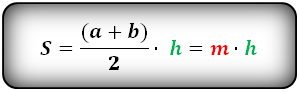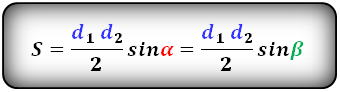Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
- Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
- Формула площади треугольника по трем сторонам
- Формула площади треугольника по двум сторонам и углу между ними
- Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
- Формулы площади квадрата
- Формула площади квадрата по длине стороны
- Формула площади квадрата по длине диагонали
- Формула площади прямоугольника
- Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
- Формула площади параллелограмма по двум сторонам и углу между ними
- Формула площади параллелограмма по двум диагоналям и углу между ними
- Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
- Формула площади ромба по длине стороны и углу
- Формула площади ромба по длинам его диагоналей
- Формулы площади трапеции
- Формула Герона для трапеции
- Формула площади трапеции по длине основ и высоте
- Формулы площади дельтоида
- Формула площади дельтоида по двум неравным сторонам и углу между ними
- Формула площади дельтоида по равным сторонам и углу между ними
- Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
- Формула площади дельтоида по двум диагоналям
- Формулы площади произвольного выпуклого четырехугольника
- Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
- Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
- Формула площади вписанного четырехугольника (формула Брахмагупты)
- Формула площади четырехугольника с вписанной окружностью
- Формула площади четырехугольника с вписанной и описанной окружностями
- Формулы площади круга
- Формула площади круга через радиус
- Формула площади круга через диаметр
- Площадь сегмента круга
- Площадь кругового сегмента через угол в градусах.
- Площадь кругового сегмента через угол в радианах.
- Формула площади эллипса
- Площадь треугольника через радиус описанной окружности
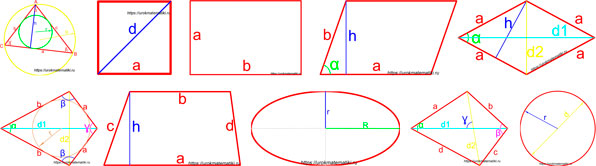
- Формулы площадей всех основных фигур
- 1. Формула площади круга через радиус или диаметр
- 2. Формула расчета площади треугольника
- 3. Площадь треугольника, формула Герона
- 4. Площадь прямоугольного треугольника по катетам
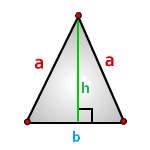
- 5. Как вычислить площадь равнобедренного треугольника ?
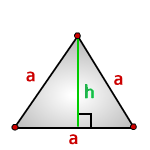
- 6. Площадь равностороннего треугольника равна:
- 7. Найти площадь треугольника, угол и две стороны
- 8. Площадь треугольника по стороне и двум углам, формула.
- 9. Формула расчета площади прямоугольника
- 10. Как рассчитать площадь квадрата через диагональ или сторону
- 11. Формулы площади параллелограмма
- 12. Площадь произвольной трапеции
- 13. Площадь равнобедренной трапеции
Видео:Формулы площади треугольника. Вписаная и описаная окружностьСкачать

Формулы площади треугольника
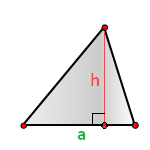
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам
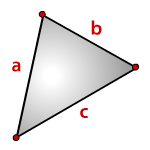
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p — a p — b p — c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
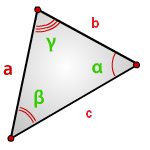
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
где a, b — стороны треугольника,
γ — угол между сторонами a и b .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
где S — площадь квадрата,
a — длина стороны квадрата.
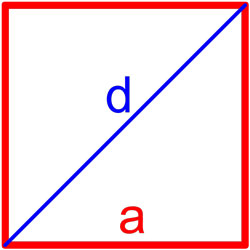
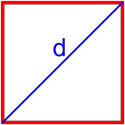
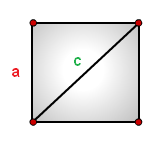
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — площадь квадрата,
d — длина диагонали квадрата.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

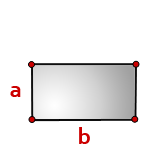
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон.
где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
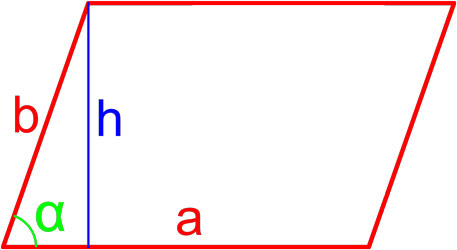
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.
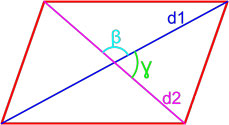
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,
где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Формулы площади ромба
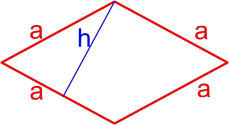
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
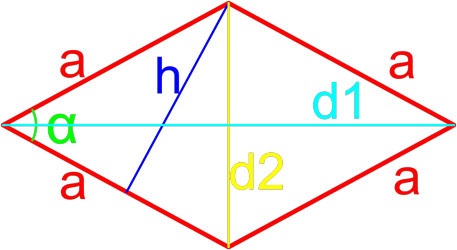
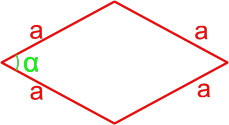
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.
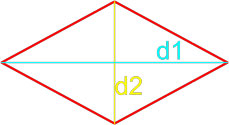
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — площадь ромба,
d1, d2 — длины диагоналей ромба.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

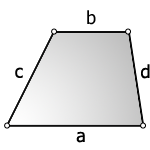
Формулы площади трапеции
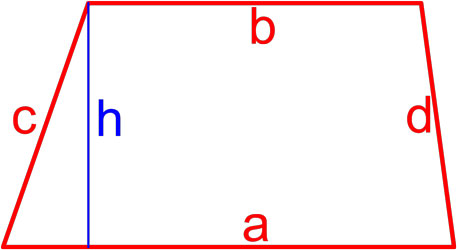
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).
Формула Герона для трапеции
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.
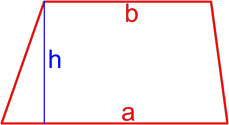
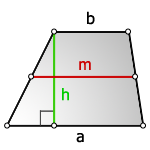
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы её оснований на высоту.
где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы площади дельтоида
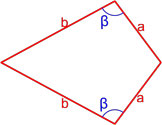
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
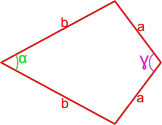
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
S = a 2 sin γ + b 2 sin α 2 ,
где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .
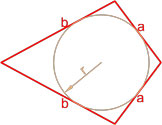
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.
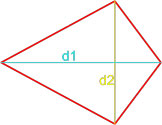
Формула площади дельтоида по двум диагоналям
Площадь дельтоида равна половине произведения длин двух диагоналей.
где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.
Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Формулы площади произвольного выпуклого четырехугольника
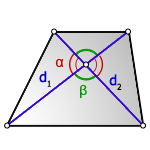
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
S = d1 · d2 · sin γ 2 ,
где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.
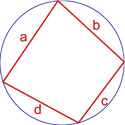
Формула площади вписанного четырехугольника (формула Брахмагупты)
Если вокруг четырехугольника можно описать окружность, то его площадь равна
S = p — a p — b p — c p — d ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.
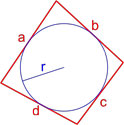
Формула площади четырехугольника с вписанной окружностью
Если в четырехугольник можно вписать окружность, то его площадь равна:
где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.
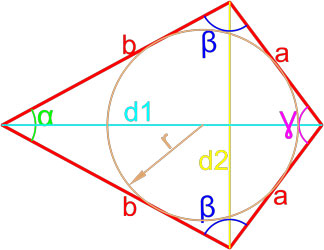
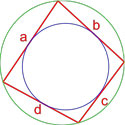
Формула площади четырехугольника с вписанной и описанной окружностями
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.
Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
где S — площадь круга,
r — радиус круга.
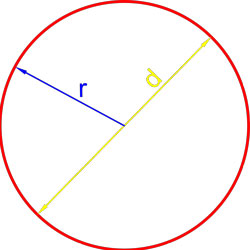
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
где S — площадь круга,
d — диаметр круга.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Площадь сегмента круга
Площадь кругового сегмента через угол в градусах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.
Площадь кругового сегмента через угол в радианах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.
Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

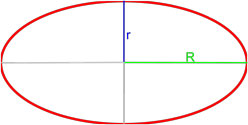
Формула площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Площадь треугольника через радиус описанной окружности
Как найти площадь треугольника через радиус описанной окружности?
Площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.
Формула для нахождения площади треугольника через радиус описанной окружности:
окружность (O; R) — описанная,
Выразим из этой формулы синус альфа
и подставим полученное выражение в первую формулу
Видео:Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Формулы площадей всех основных фигур
Видео:Построить описанную окружность (Задача 1)Скачать

1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
r — радиус круга
D — диаметр
Формула площади круга, (S):
Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
Видео:Площадь треугольника через радиус описанной окружности: ОГЭ - ЕГЭСкачать

3. Площадь треугольника, формула Герона
a , b , c , — стороны треугольника
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
Видео:Радиус вписанной окружности, формулу через площадь и полупериметрСкачать

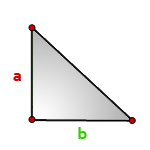
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a , b — катеты треугольника
Формула площади прямоугольного треугольника, (S):
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

5. Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b , ( S ):
Формула площади треугольника через, стороны a , b , (S):

Видео:Формула радиуса описанной окружности треугольника. Геометрия 9 классСкачать

6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь треугольника только через сторону a , (S):
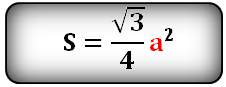
Площадь треугольника только через высоту h , ( S ):
Площадь треугольника через сторону a и высоту h , (S):
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
a , b , c — стороны треугольника
α , β , γ — углы
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
8. Площадь треугольника по стороне и двум углам, формула.
a , b , c — стороны треугольника
α , β , γ — противолежащие углы
Площадь треугольника через сторону и два угла (S):
9. Формула расчета площади прямоугольника
b — длина прямоугольника
a — ширина
Формула площади прямоугольника, (S):
10. Как рассчитать площадь квадрата через диагональ или сторону
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a , (S):
Формула площади квадрата через диагональ c , (S):
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α , β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
12. Площадь произвольной трапеции
1. Формула площади трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S):
2. Формула площади трапеции через диагонали и угол между ними
d 1, d 2 — диагонали трапеции
α , β — углы между диагоналями
Формула площади трапеции, (S):
3. Формула площади трапеции через четыре стороны
b — верхнее основание
a — нижнее основание
c, d — боковые стороны
Формула площади трапеции, (S):
13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):