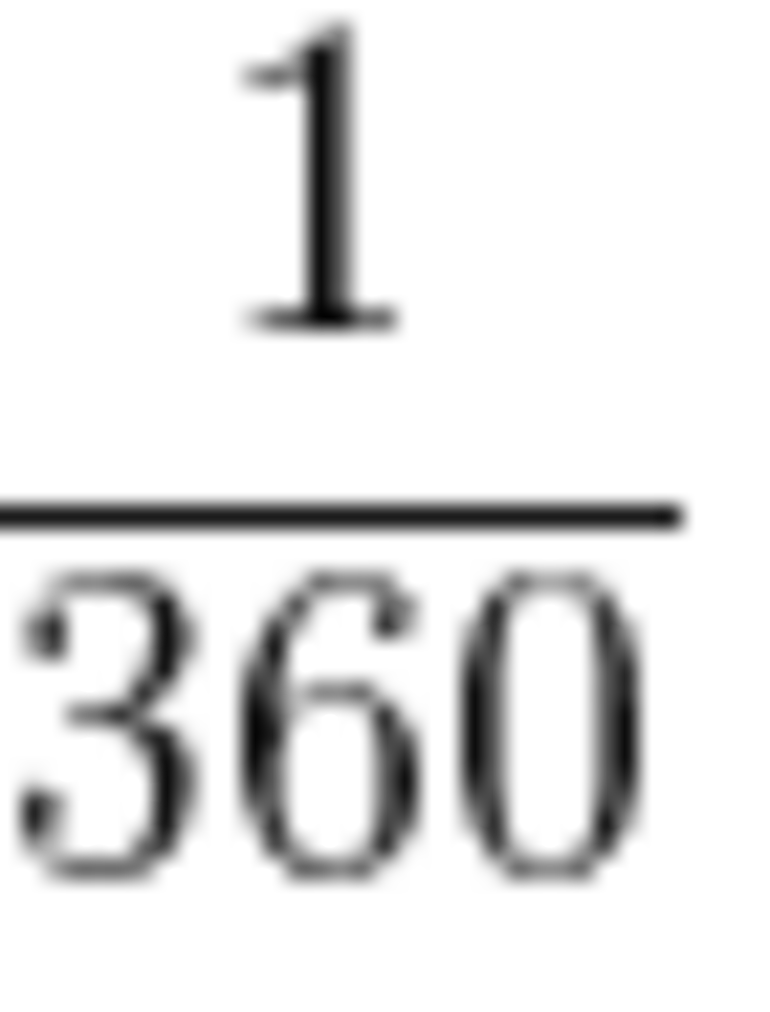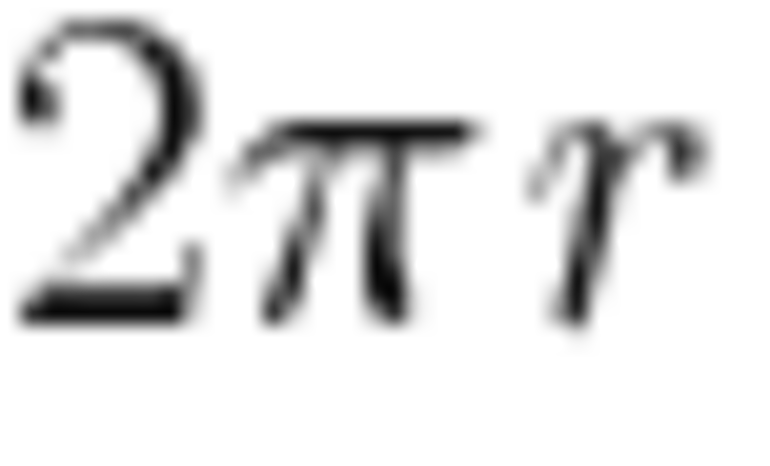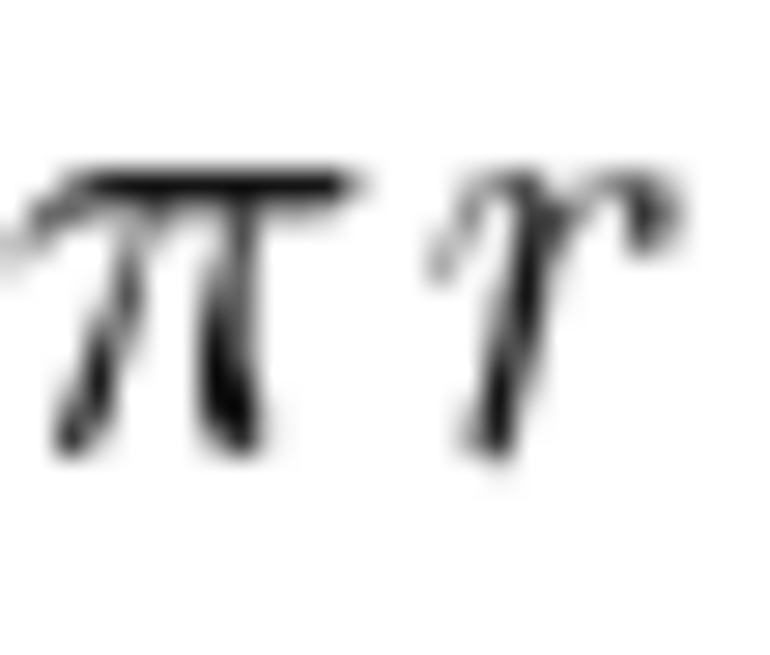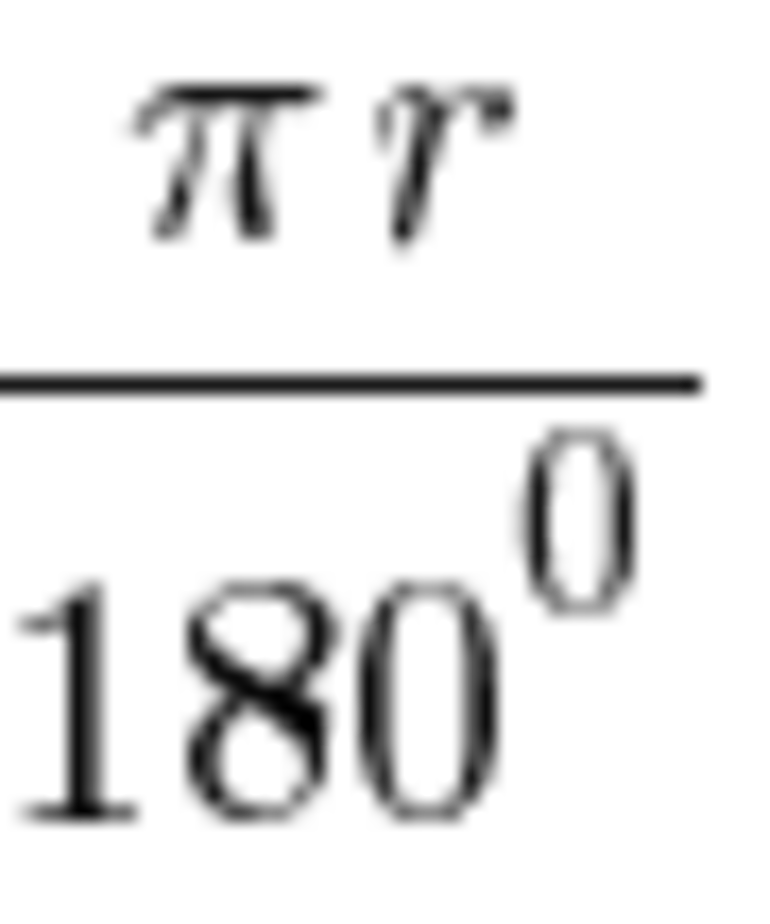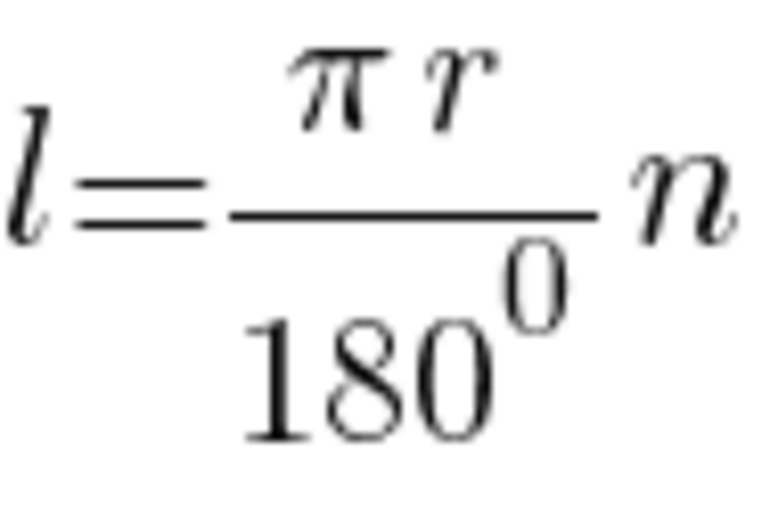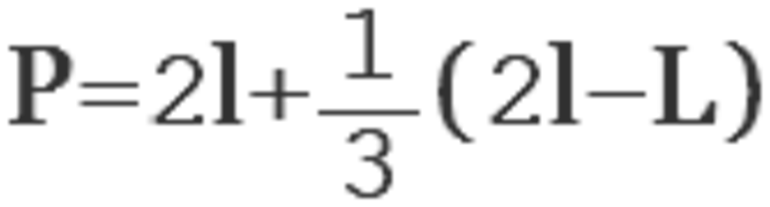Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение окружности
- Отрезки в окружности
- Определение окружности
- Отрезки в окружности
- Дуга в окружности
- Углы в окружности
- Длина окружности, длина дуги
- Площадь круга и его частей
- Теорема синусов
- Примеры решений заданий из ОГЭ
- Длина дуги окружности — формула, обозначение, примеры расчета
- Необходимость расчётов
- Градусная мера
- Применение хорды и высоты
- Практика с задачами
- Усложнение формулы
- Площадь круга и его частей. Длина окружности и ее дуг
- Основные определения и свойства
- Формулы для площади круга и его частей
- Формулы для длины окружности и её дуг
- Площадь круга
- Длина окружности
- Длина дуги
- Площадь сектора
- Площадь сегмента
Видео:72. Градусная мера дуги окружностиСкачать
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности .
Видео:8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Видео:Длина дуги окружности. 9 класс.Скачать

Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности .
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Видео:Длина окружности. 9 класс.Скачать

Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α
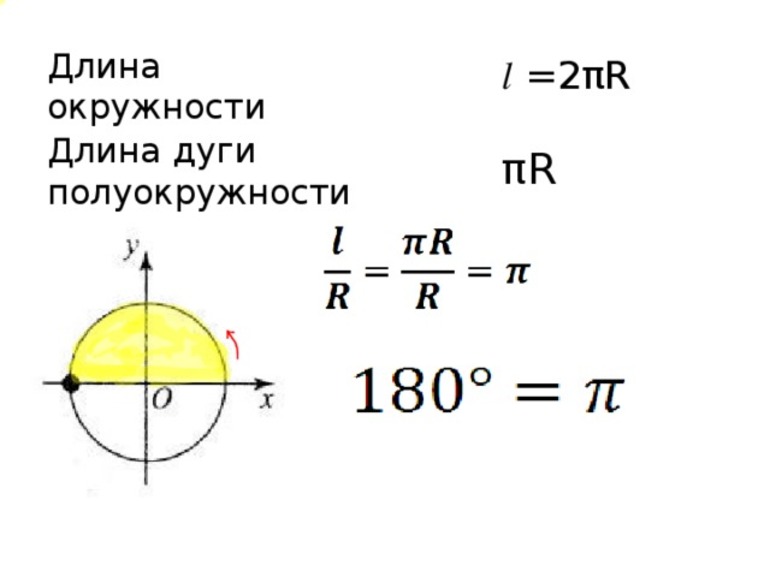
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

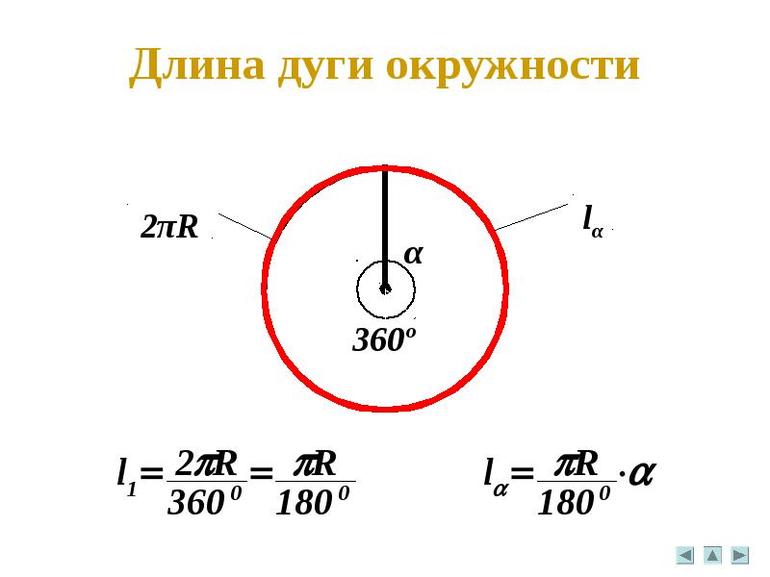
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Длина дуги окружности , на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
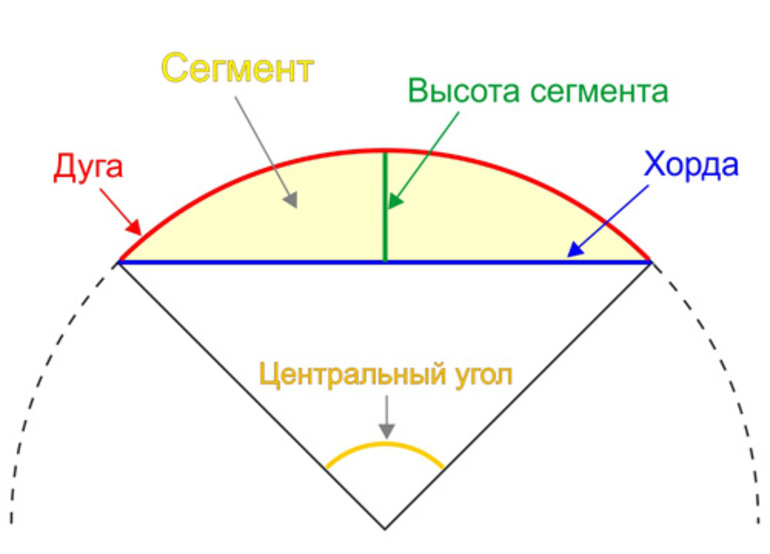
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Видео:Геометрия 8 класс (Урок№26 - Градусная мера дуги окружности. Центральные углы.)Скачать

Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Длина дуги окружности — формула, обозначение, примеры расчета
Видео:Длина окружности. Математика 6 класс.Скачать

Необходимость расчётов
Геометрическими формулами, связанными с подсчетом площади сектора, объема сегмента и периметра полукруга, следует виртуозно владеть людям, связавшим свою жизнь со строительством или благоустройством территорий. Чтобы обновить после зимы элементы архитектуры городского парка и закрасить дефекты абстрактных скульптур, не нужно вспоминать сложные уравнения, достаточно применить знание геометрических формул.
К примеру, для правильного нахождения веса декоративного камня, предназначенного для окантовки части клумбы, нужно уметь быстро посчитать размер полуокружности на поверхности ландшафта. Затем необходимо определиться с ценой и принять решение, какой камень можно покупать с учетом сметы. Аналогичная задача возникает при строительстве альпийской горки. Тяжесть камня обеспечит круговую укладку, это свойство позволит высадить декоративные растения в запланированных местах сечения, придав конструкции форму трапеции.
Что представляет собой часть клумбы? Это сектор геометрической фигуры. Внешняя его часть — окантовка клумбы — чаще всего представляет собой дугу окружности. Существует две методики вычисления этой величины:
- градусная (с привязкой к центральному углу);
- по формуле Гюйгенса (с использованием хорды).
Определение методики расчета в полевых условиях зависит от наличия инструментов и особенностей рельефа местности. Но сначала немного теории. Дугой называют часть окружности, расположенную между двумя произвольными точками, находящимися на ней.
Для удобства рассмотрим пример с двумя точками A и B, расположенными на окружности на небольшом расстоянии друг от друга. Они делят её на 2 части — большую и меньшую. Каждая из них называется дугой окружности.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Градусная мера
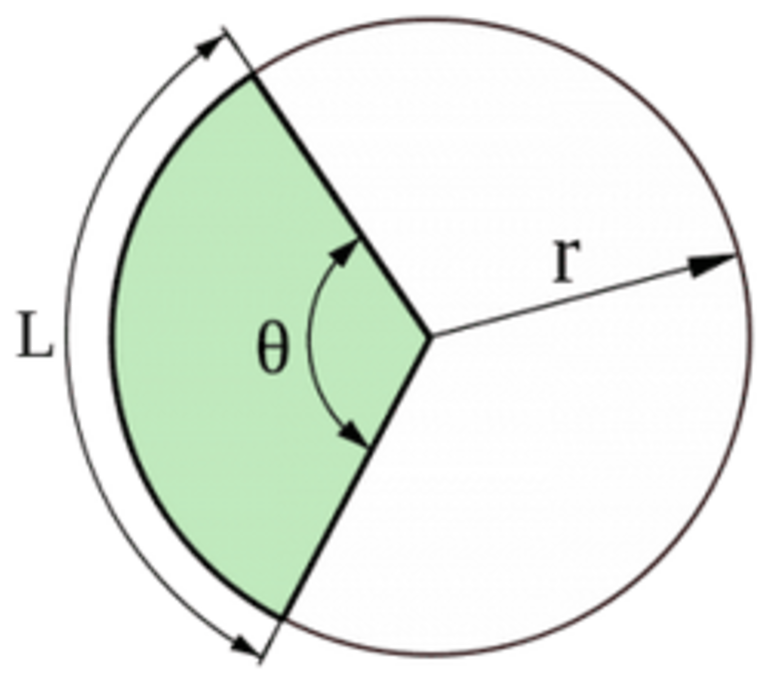
Длина дуги между точками окружности является функцией центрального угла, образованного радиусами круга (см. рисунок) в прямо пропорциональной зависимости. На этом основана градусная мера.
За 1° дуги принимают часть окружности.
Поскольку L равна , то развернутому углу 180° будет соответствовать длина дуги .
Если значение угла равно 1°, формула выглядит так: .
Следовательно, формула длины дуги окружности с центральным углом n° будет выражаться следующим образом: .
Определим значение l для угла 120° с радиусом, равным 5 мм: l=3,14*30*5/180=2,62 мм.
Видео:ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать

Применение хорды и высоты
Существует методика расчета длины дуги по хорде и высоте перпендикуляра. Она получила название формулы Гюйгенса. Хорда представляет собой часть прямой, расположенной внутри окружности. Проходящая через центр хорда называется диаметром.
Формулу Гюйгенса применяют, если центральный угол меньше 60 градусов. Для проведения вычислений необходимо сначала соединить точки окружности прямой линией. Это будет хорда. Далее нужно провести перпендикуляр из ее середины, а из точки соприкосновения перпендикуляра с дугой начертить две прямые линии к концам хорды.
Получился равнобедренный треугольник, стороны которого обозначим l , а саму хорду назовем L . Для углов более 60 градусов формулу Гюйгенса не стоит использовать, поскольку при расчетах может возникнуть ошибка. Чем больше угол, тем значительней будет погрешность.
Замерив хорды L и l, можно получить значение дуги, обозначенной на рисунке синим цветом. Если L равна 30 мм, а l — 20 мм, то Р=2*20+3,33=43,33 мм.
Теперь, когда существует понимание методики расчета, можно воспользоваться онлайн-калькулятором. Этот инструмент хорош для проверки полученного экспериментальным путем результата, особенно при обработке большого количества данных, когда необходимо быстро получить ответ.
Онлайн-калькулятор позволяет сохранять полученные значения в буферной памяти компьютера. Оформить данные в виде произвольной таблицы или графика в системе координат не составит труда. Длина дуги окружности по онлайн-калькулятору считается с использованием любой из двух формул: либо по градусной мере, либо по хорде и высоте. Образно говоря, эти формулы являются синонимами, они взаимозаменяемы.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Практика с задачами
Нужно сказать несколько слов об изучении геометрии в средних классах общеобразовательной школы. Существует категория учащихся, для которых формулы сложны для восприятия. Таким ученикам требуется наглядный материал.
На уроке геометрии при изучении материала по вычислениям параметров окружности можно провести практическое занятие. Для этого следует предварительно подготовиться: сделать небольшой чертеж-проекцию гимнастического кольца. Цель занятия — научиться использовать формулы в процессе работы. Ход урока:
- Попросить дежурного ученика принести из спортивного зала гимнастическое кольцо (хула-хуп) небольшого диаметра.
- Отметить фломастером или цветным мелком 3 точки на наружной стороне кольца. После этого оно окажется поделенным на несколько секторов.
- Сделать проекцию кольца на школьной доске с нанесенными точками. На чертеже обозначить центр круга, провести диаметр. Затем нужно соединить отмеченные на окружности точки радиусами с центром круга и хордами между собой.
- Провести все замеры. Получить значения всех параметров и записать на доске. Её предварительно разделить на две части: в центре, доступном для обзора, будут значения центральных углов АОВ и ВОС, диаметр, длина прямых линий АВ, ВС и АС.
- Ответы (искомые значения) записать в правой части доски и прикрыть шторкой до момента окончания практического занятия.
Далее следует разделить класс на 4 небольших группы. Каждой из них нужно дать задание по проведению вычислений с использованием изученных формул.
- группа №1 вычисляет длину дуги между точками А и В, используя градусную меру центрального угла АОВ;
- вторая группа получает аналогичное задание для отрезка между точками В и С;
- третья группа вычисляет искомый параметр между точками А и С, используя длину хорды АС и вспомогательных линий АВ и ВС;
- группа №4 работает с точками А и С, применяя значения угла АОС.
На выполнение задания отводится 12 минут. После истечения времени от каждой из четырех групп выходит ученик, поясняет формулу и записывает на доске полученный результат. Эти ответы сравниваются с уже готовыми замерами, записанными ранее на правой стороне доски.
Следующие 7 минут урока отводятся на обсуждение полученного результата и анализа возникновения погрешности.
Видео:Длина дуги окружности. Практическая часть. 9 класс.Скачать
Усложнение формулы
Группе продвинутых учеников предлагается задание «Как изменить градусную формулу?». Можно ли найти значение радиуса, используя другие геометрические выражения, например, представить его как половину диаметра круга? В этом случае формулы будет выглядеть следующим образом: r=1/2d, тогда l= πd/360*n.
Если использовать формулу вычисления площади круга и выразить радиус через неё, тогда можно получить s=πr 2 .
Обозначаться радиус будет интересно — в виде производной квадратного корня. Вывести формулу нетрудно, это станет прекрасной ментальной гимнастикой для учащихся.
Базовая цель уроков математики — развитие аналитического мышления учащихся достигается в процессе обсуждения и сравнения различных методик расчета. В качестве дополнительного задания можно предложить ученикам посчитать значение кривой линии наружного края школьной клумбы. Затем следует попросить обосновать свои расчеты.
Использование наглядности поможет учащимся подружиться с формулами, увидеть роль геометрии в повседневной практической жизни и облегчить усвоение конкретного материала.
Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Площадь круга и его частей. Длина окружности и ее дуг
 Основные определения и свойства. Число π Основные определения и свойства. Число π |
 Формулы для площади круга и его частей Формулы для площади круга и его частей |
 Формулы для длины окружности и ее дуг Формулы для длины окружности и ее дуг |
 Площадь круга Площадь круга |
 Длина окружности Длина окружности |
 Длина дуги Длина дуги |
 Площадь сектора Площадь сектора |
 Площадь сегмента Площадь сегмента |
Видео:Градусная мера дуги окружности. Центральные углыСкачать

Основные определения и свойства
| Фигура | Рисунок | Определения и свойства | ||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||
| Дуга |  | |||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||
| Сектор |  | |||||||||||||||||||||||||
| Сегмент |  | |||||||||||||||||||||||||
| Правильный многоугольник |  | |||||||||||||||||||||||||
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Часть окружности, расположенная между двумя точками окружности

Конечная часть плоскости, ограниченная окружностью

Часть круга, ограниченная двумя радиусами

Часть круга, ограниченная хордой

Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Видео:Радианная мера угла. 9 класс.Скачать

Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула | |||||||||
| Площадь круга |  | ||||||||||
| Площадь сектора |  | ||||||||||
| Площадь сегмента |  |
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга


если величина угла α выражена в радианах

если величина угла α выражена в градусах


если величина угла α выражена в радианах

если величина угла α выражена в градусах
Видео:Как найти длину дуги окружности центрального угла. Геометрия 8-9 классСкачать

Формулы для длины окружности и её дуг
| Числовая характеристика | Рисунок | Формула | |
| Длина окружности |  | ||
| Длина дуги |  |
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах
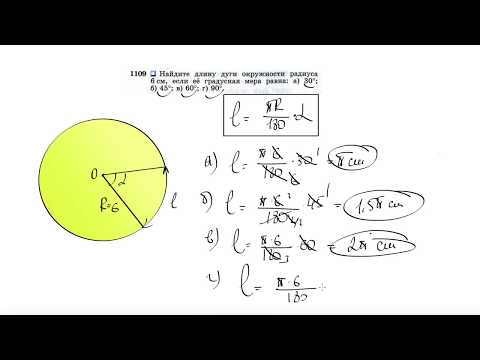
Видео:№1109. Найдите длину дуги окружности радиуса 6 см, если ее градусная мера равна: а) 30°; б) 45°Скачать
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Видео:Площадь сектора и сегмента. 9 класс.Скачать

Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем