На чертеже изображен треугольник

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Остроугольные	Тупоугольные	Прямоугольные
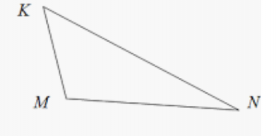
Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС.	Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой.	Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

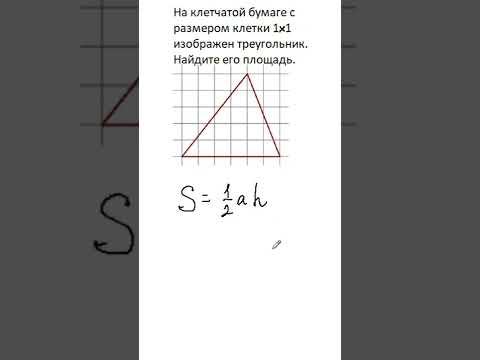
Видео:Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

На чертеже изображен треугольник

Глава 2. Треугольники

Как, не накладывая треугольники один на другой, узнать, равны ли они? Какими особыми свойствами обладают равнобедренный и равносторонний треугольники? Как «устроена» теорема? На эти и многие другие вопросы вы найдёте ответы в данной главе.

§ 7. Равные треугольники. Высота, медиана, биссектриса треугольника

Рассмотрим три точки A , B , C , не лежащие на одной прямой. Соединим их отрезками AB , BC , CA . Полученная фигура ограничивает часть плоскости, выделенную на рисунке 108 зелёным цветом. Эту часть плоскости вместе с отрезками AB , BC и CA называют треугольником .

Точки A , B , C называют вершинами , а отрезки AB , BC , CA — сторонами треугольника.

Треугольник называют и обозначают по его вершинам. Треугольник, изображённый на рисунке 108, обозначают так: ∆ ABC , или ∆ BCA , или ∆ ACB (читают: «треугольник ABC », «треугольник BCA », «треугольник ACB ») и т. д.

Углы BAC , ABC , BCA (рис. 109) называют углами треугольника ABC .

В треугольнике ABC (рис. 109), например, угол B называют углом , противолежащим стороне AC , углы A и C — углами , прилежащими к стороне AC , сторону AC — сто роной, противолежащей углу B , стороны AB и AC — сторонами, прилежащими к углу A .

Периметром треугольника называют сумму длин всех его сторон.

Периметр обозначают буквой P . Например, для периметра треугольника MNK используют обозначение P MNK .

Треугольник называют остроугольным, если все его углы острые ( рис. 110, а ).

Треугольник называют прямоугольным, если один из его углов прямой ( рис. 110, б ).

Треугольник называют тупоугольным, если один из его углов тупой ( рис. 110, в ).

Два треугольника называют равными, если их можно совместить наложением.

На рисунке 111 изображены равные треугольники ABC и A 1 B 1 C 1 . Записывают: ∆ ABC = ∆ A 1 B 1 C 1 . Эти треугольники можно совместить так, что вершины A и A 1 , B и B 1 , C и C 1 совпадут. Тогда можно записать: ∠ A = ∠ A 1 , ∠ B = ∠ B 1 , ∠ C = ∠ C 1 , AB = A 1 B 1 , BC = B 1 C 1 , CA = C 1 A 1 .

Те стороны и те углы, которые совмещаются при наложении треугольников, называют соответственными сторонами и соответственными углами . Так, например, на рисунке 111 стороны AC и A 1 C 1 , углы A и A 1 — соответственные.

Обычно на рисунках равные стороны отмечают одинаковым количеством чёрточек, а равные углы — одинаковым количеством дуг (рис. 111).

Заметим, что в равных треугольниках против соответственных углов лежат соответственные стороны , и наоборот: против соответственных сторон лежат соответственные углы .

Основное свойство равенства треугольников

Для данного треугольника ABC и луча A 1 M существует треугольник A 1 B 1 C 1 , равный треугольнику ABC , такой, что AB = A 1 B 1 , BС = B 1 C 1 , AC = A 1 C 1 и сторона A 1 B 1 принадлежит лучу A 1 M , а вершина C 1 лежит в заданной полуплоскости относительно прямой A 1 M ( рис. 112 ).

Через точку, не принадлежащую данной прямой, проходит только одна прямая, перпендикулярная данной.

Рассмотрим прямую a и не принадлежащую ей точку O . Предположим, что через точку O проходят две прямые OA и OB , перпендикулярные прямой a (рис. 113).

В силу основного свойства равенства треугольников существует треугольник O 1 AB , равный треугольнику OAB (рис. 114). Тогда ∠ OAB = ∠ O 1 AB = 90°. Отсюда ∠ OAO 1 = 180°, а значит, точки O , A , O 1 лежат на одной прямой.

Аналогично доказывают, что точки O , B , O 1 также лежат на одной прямой. Но тогда прямые OA и OB имеют две точки пересечения: O и O 1 . А это противоречит теореме 1.1. Следовательно, наше предположение неверно. Тогда через точку О проходит одна прямая, перпендикулярная прямой а .

Возможно, вы заметили, что определения равных отрезков, равных углов и равных треугольников очень похожи. Поэтому целесообразно принять следующее определение равных фигур.

Две фигуры называют равными, если их можно совместить наложением.

На рисунке 115 изображены равные фигуры Ф 1 и Ф 2 . Пишут: Ф 1 = Ф 2 .

Любые две прямые (два луча, две точки) равны.

Перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону, называют высотой треугольника.

На рисунке 116 отрезки BB 1 и CC 1 — высоты треугольника ABC .

Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называют медианой треугольника.

На рисунке 117 отрезок AM — медиана треугольника ABC .

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны, называют биссектрисой треугольника.

На рисунке 118 отрезок BL — биссектриса треугольника ABC .

Каждый треугольник имеет три высоты, три медианы и три биссектрисы.

Часто длины сторон треугольника, противолежащих углам A , B , C , обозначают соответственно a , b , c . Длины высот обозначают h a , h b , h c , медиан — m a , m b , m c , биссектрис — l a , l b , l c . Индекс показывает, к какой стороне проведён отрезок (рис. 119).

1. Как называют и обозначают треугольник?
2. Что называют периметром треугольника?
3. Какие существуют виды треугольников в зависимости от вида их углов?
4. Какой треугольник называют прямоугольным? Тупоугольным? Остроугольным?
5. Какие два треугольника называют равными?
6. Как называют пары сторон и пары углов равных треугольников, которые совмещаются при наложении?
7. Какие две фигуры называют равными?
8. Что называют высотой треугольника?
9. Что называют медианой треугольника?
10. Что называют биссектрисой треугольника?
11. Сколько у каждого треугольника высот? Медиан? Биссектрис?

132. Начертите треугольник:

Проведите из каждой вершины треугольника высоту.

133. Перерисуйте в тетрадь рисунок 120, проведите высоту, общую для трёх изображённых треугольников. У какого из них эта высота расположена вне треугольника?

134. Перерисуйте в тетрадь треугольники, изображённые на рисунке 121, проведите в каждом из них три высоты.

135. Начертите произвольный треугольник и проведите все его медианы.

Видео:ОГЭ, математика, задание 18| Треугольник на клетчатой бумагеСкачать

Треугольники. Признаки равенства треугольников

Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

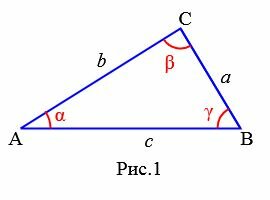
Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

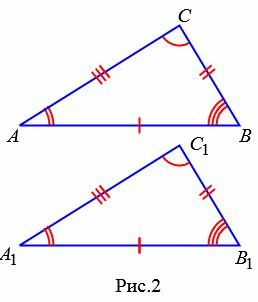
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

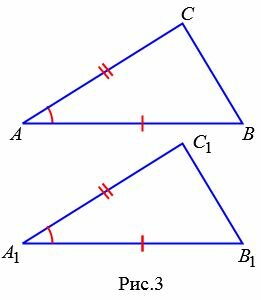Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Видео:Сколько всего треугольников изображено на рисунке?Скачать

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

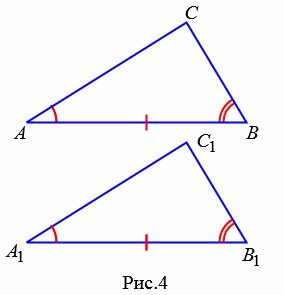Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Видео:Сколько треугольников на рисунке? Простая задача, которая позволяет загрузить даже студентовСкачать

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

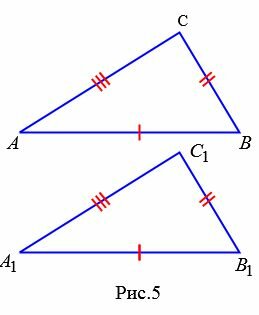Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

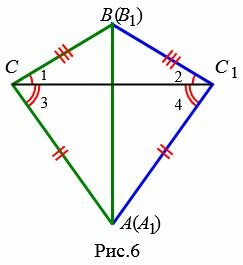Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

.

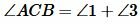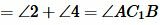Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

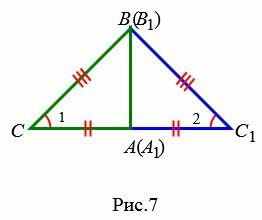Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

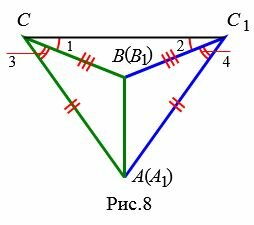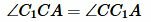
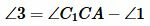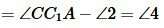Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и и, следовательно:

.

Имеем AC=A₁C₁, BC=B₁C₁ 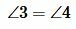и по первому признаку равенства треугольников . Теорема доказана.

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

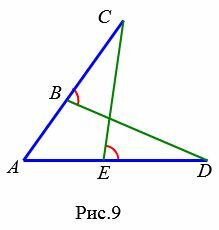Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

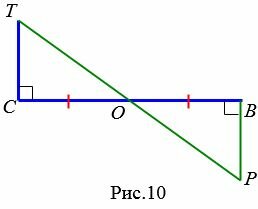Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .

📺 Видео

Построение треугольника в трёх проекцияхСкачать

Построение натуральной величины треугольника методом вращенияСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Лайфхак! Площади всех фигур #огэ #математика #shortsСкачать

Секретное свойство медианыСкачать

Лекция 4. ПлоскостьСкачать

ПРИЕМЫ РАБОТЫ С ЧЕРТЕЖНЫМ ИНСТРУМЕНТОМ. Линии чертежа. Видео для начинающихСкачать

Лекция №4 Чертеж прямой. Следы прямой. Прямые общего и частного положения. Взаимное положение прямыхСкачать

Изображение резьбы на чертежеСкачать

Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

Порядок построения изображения на чертежахСкачать