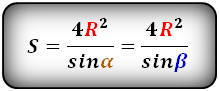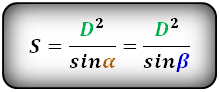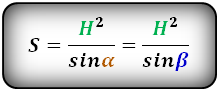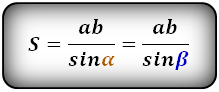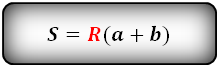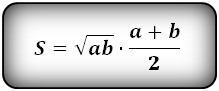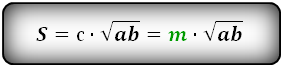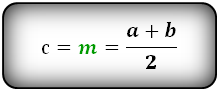Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.
Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.
Площадь трапеции, можно измерить, в единицах
измерения в квадрате: мм 2 , см 2 , м 2 и км 2 и так далее.
Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.
- Формулы площади трапеции
- Площадь любых трапеций
- Площадь равнобедренной трапеции
- Определения трапеции
- Элементы трапеции
- Площадь равнобедренной трапеции
- Трапеция. Формулы, признаки и свойства трапеции
- Основные свойства трапеции
- Сторона трапеции
- Формулы определения длин сторон трапеции:
- Средняя линия трапеции
- Формулы определения длины средней линии трапеции:
- Высота трапеции
- Формулы определения длины высоты трапеции:
- Диагонали трапеции
- Формулы определения длины диагоналей трапеции:
- Площадь трапеции
- Формулы определения площади трапеции:
- Периметр трапеции
- Формула определения периметра трапеции:
- Окружность описанная вокруг трапеции
- Формула определения радиуса описанной вокруг трапеции окружности:
- Окружность вписанная в трапецию
- Формула определения радиуса вписанной в трапецию окружности
- Другие отрезки разносторонней трапеции
- Формулы определения длин отрезков проходящих через трапецию:
- 🎦 Видео
Формулы площади трапеции
Площадь любых трапеций
Ⅰ. Площадь трапеции через основания и высоту:
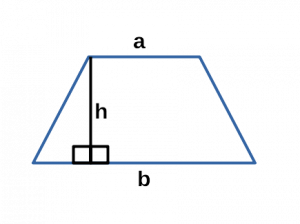
[ S = frac cdot h ]
a,b — основания трапеции;
h — высота трапеции;
Ⅱ. Площадь трапеции через высоту и среднюю линию:
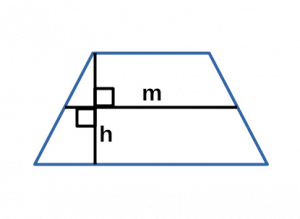
[ S = mh ]
m — средняя линия трапеции;
h — высота трапеции;
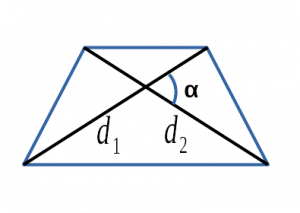
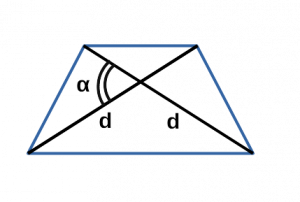
Ⅲ. Площадь трапеции через диагонали и угол между ними:
[ S =fracd_1d_2 cdot sin alpha ]
( d_1, d_2 ) - диагонали трапеции;
sin α — синус угла альфа в трапеции;
Ⅳ. Площадь трапеции через периметр, высоту и боковые стороны:
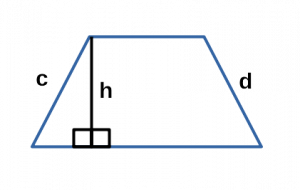
[ S = frach ]
P — периметр трапеции;
c,d — боковые стороны трапеции;
h — высота трапеции;
Ⅴ. Площадь трапеции через основания и боковые стороны:
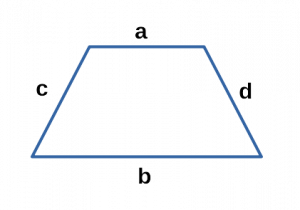
a,b — основания трапеции;
с,d — боковые стороны трапеции;
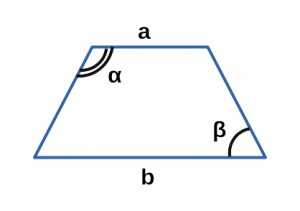
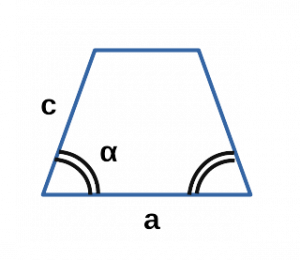
Ⅵ. Площадь трапеции через основания и углы:
a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;
Площадь равнобедренной трапеции
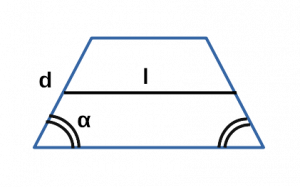
Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:
[ S = ld cdot sin α ]
l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅱ. Площадь трапеции через диагонали и синус угла:
[ S = frac cdot sin α ]
d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
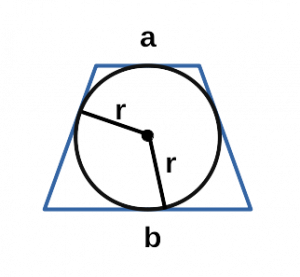
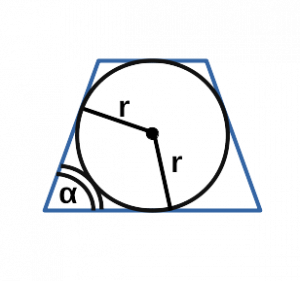
Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:
r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
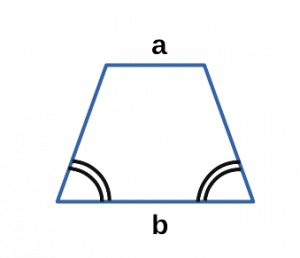
Ⅳ. Площадь трапеции через основания:
a, b — основания равнобедренной трапеции;
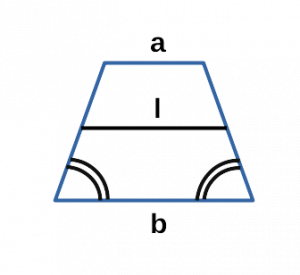
Ⅴ. Площадь трапеции через основания и среднюю линию:
l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅵ. Площадь трапеции через синус угла и стороны:
[ S = c cdot sin α cdot (a-c cdot cos α) ]
a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;
Ⅶ. Площадь трапеции через угол и радиус вписанной окружности:
r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Определения трапеции
Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.
Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:
- Обычная / стандартная трапеция: четыре угла и четыре стороны не равны.
- Равнобедренная / равнобочная / равнобоковая трапеция:
два угла при основании равны, две боковые стороны равны. - Прямоугольная / прямаятрапеция: один из углов прямой.
Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.
Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.
Элементы трапеции
Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.
Основание трапеции — это сторона, противолежащая
сторона которой параллельна.
Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.
Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.
Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.
Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.
Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.
Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.
Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, ( S ):
Формула площади равнобедренной трапеции через стороны и угол, ( S ):
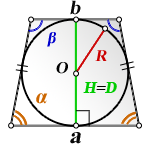
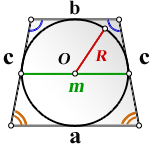
2. Формулы площади равнобедренной трапеции если в нее вписана окружность
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, ( S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
R — радиус вписанной окружности
m — средняя линия
O — центр вписанной окружности
c — боковые стороны
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию ( S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, ( S ):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c — боковая сторона
m — средняя линия трапеции
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, ( S ):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, ( S ):
Видео:Площадь трапецииСкачать
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
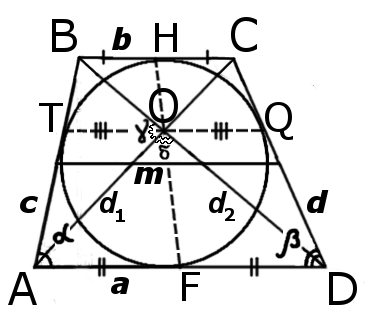 | 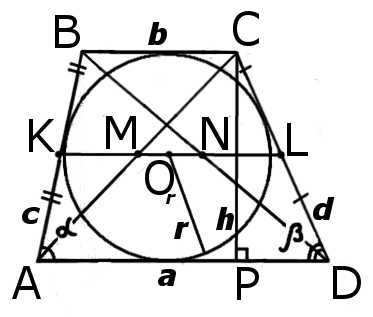 |
| Рис.1 | Рис.2 |
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
| m = | a + b |
| 2 |
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Видео:8 класс, 15 урок, Площадь трапецииСкачать

Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Видео:Площадь трапецииСкачать

Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
| m = | a + b |
| 2 |
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
| h = | 2S |
| a + b |
5. Формула высоты трапеции через площадь и длину средней линии:
| h = | S |
| m |
Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) | a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Видео:Задача про трапецию, описанную около окружностиСкачать

Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
| S = | ( a + b ) | · h |
| 2 |
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Видео:Лучший способ найти площадь кругаСкачать

Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
| p = | a + c + d 1 |
| 2 |
a — большее основание
Видео:Площадь трапеции. Быстрый способ запомнить формулуСкачать

Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
🎦 Видео
Радиус описанной окружности трапецииСкачать

Геометрия 8 класс. Площадь трапецииСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Длина окружности. Площадь круга. 6 класс.Скачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Площадь круга. Математика 6 класс.Скачать

ОГЭ. Математика. Задание 26 | Прямоугольная трапеция и окружность | Борис Трушин |Скачать