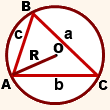
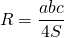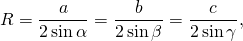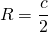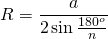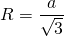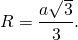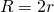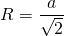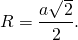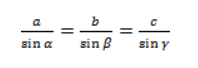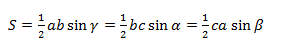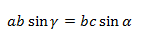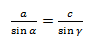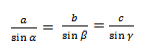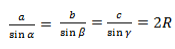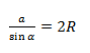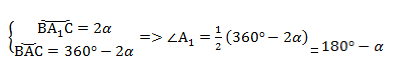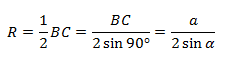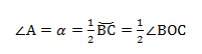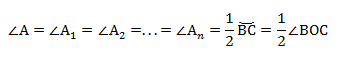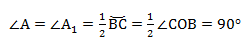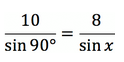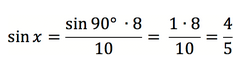Формула описанной окружности неправильного треугольника (2 видео)

Нахождение радиуса описанной вокруг треугольника окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Содержание

Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Прямоугольный треугольник
Равносторонний треугольник
Примеры задач
Радиус описанной окружности
Теорема синусов
Доказательство теоремы синусов
Доказательство следствия из теоремы синусов
Теорема о вписанном в окружность угле
Примеры решения задач
Запоминаем
📸 Видео

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы вычисления радиуса описанной окружности

Произвольный треугольник

Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.

Равносторонний треугольник

Радиус описанной около правильного треугольника окружности вычисляется по формуле:

где a – сторона треугольника.

Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Примеры задач

Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.

Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:

Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:

Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.

Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:

Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Радиус описанной окружности

Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.

Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):

где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.

у остроугольного треугольника — внутри треугольника;

у прямоугольного — на середине гипотенузы;

у тупоугольного — вне треугольника, напротив тупого угла.

Радиус описанной окружности для прямоугольного треугольника

Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:

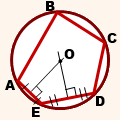
Окружность, описанная около многоугольника

Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Радиус описанной около многоугольника окружности находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.

Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.

Радиус окружности, описанной около правильного многоугольника

Формула радиуса описанной окружности для правильного многоугольника

где a — длина стороны многоугольника, n — количество его сторон.

Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.

Радиус описанной окружности правильного треугольника

Формула радиуса описанной окружности для правильного треугольника

Если без иррациональности в знаменателе —

У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:

Радиус описанной окружности квадрата

Формула радиуса описанной окружности для квадрата

Если без иррациональности в знаменателе —

Радиус описанной окружности правильного шестиугольника

Формула радиуса описанной окружности для правильного шестиугольника

Видео:Радиус описанной окружности трапецииСкачать

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Формула радиуса описанной окружности треугольника. Геометрия 9 классСкачать

Доказательство теоремы синусов

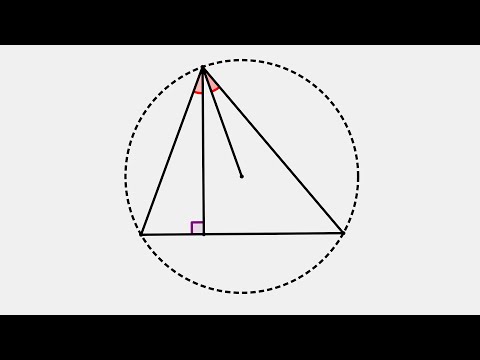
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

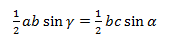
Формула описанной окружности неправильного треугольника

На b сокращаем, синусы переносим в знаменатели:

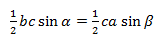
bc sinα = ca sinβ

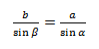
Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

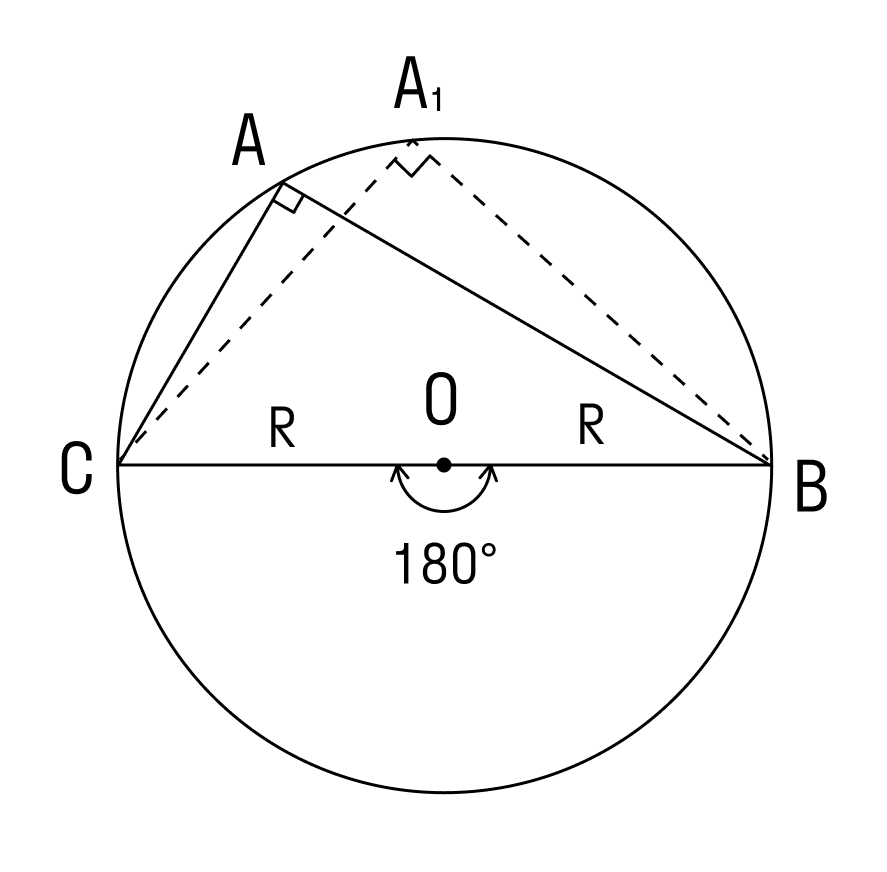
1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

sin120° = sin(180° — 60°) = sin60° = 3/√2;
sin150° = sin(180° — 30°) = sin30° = 1/2;
sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

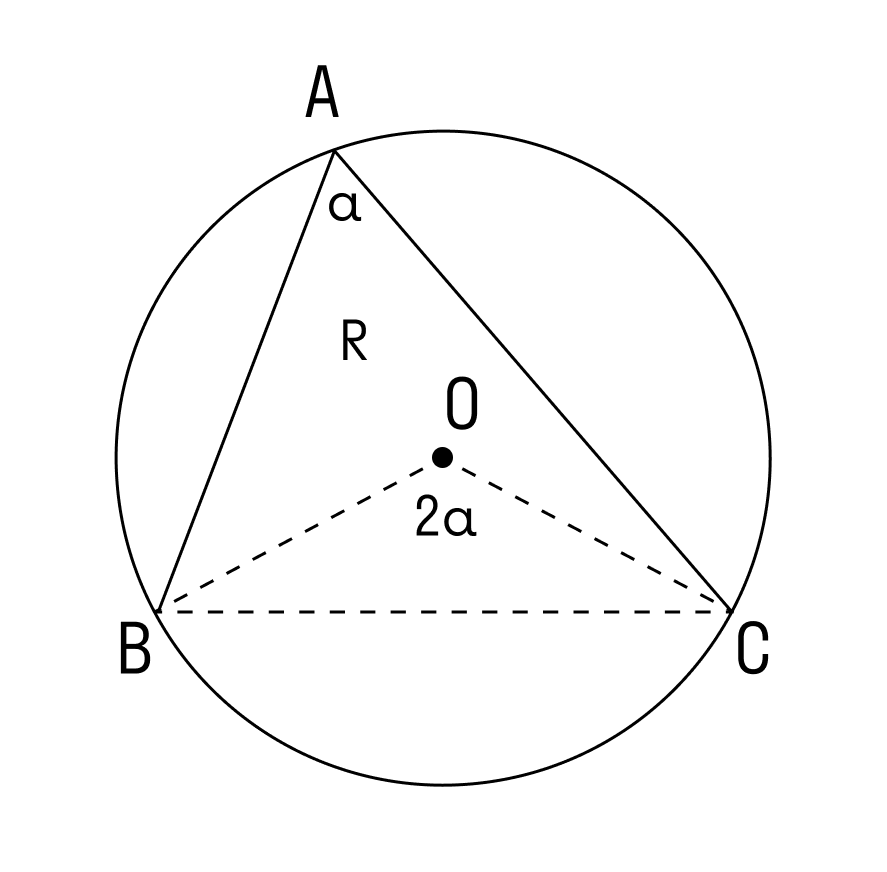
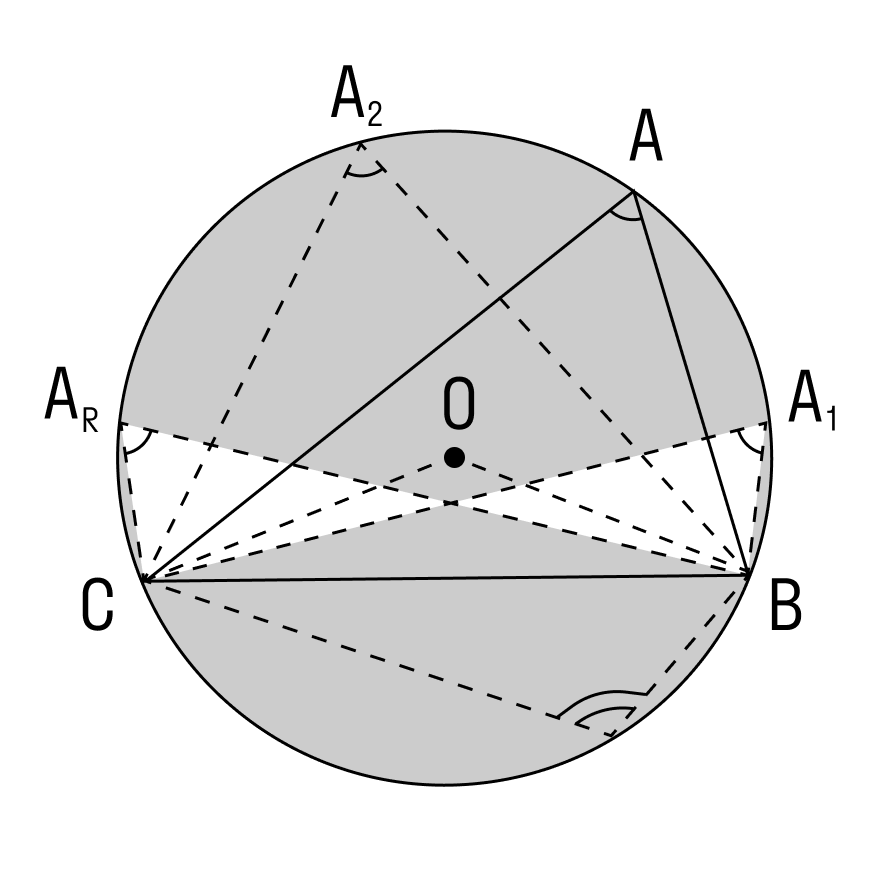
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

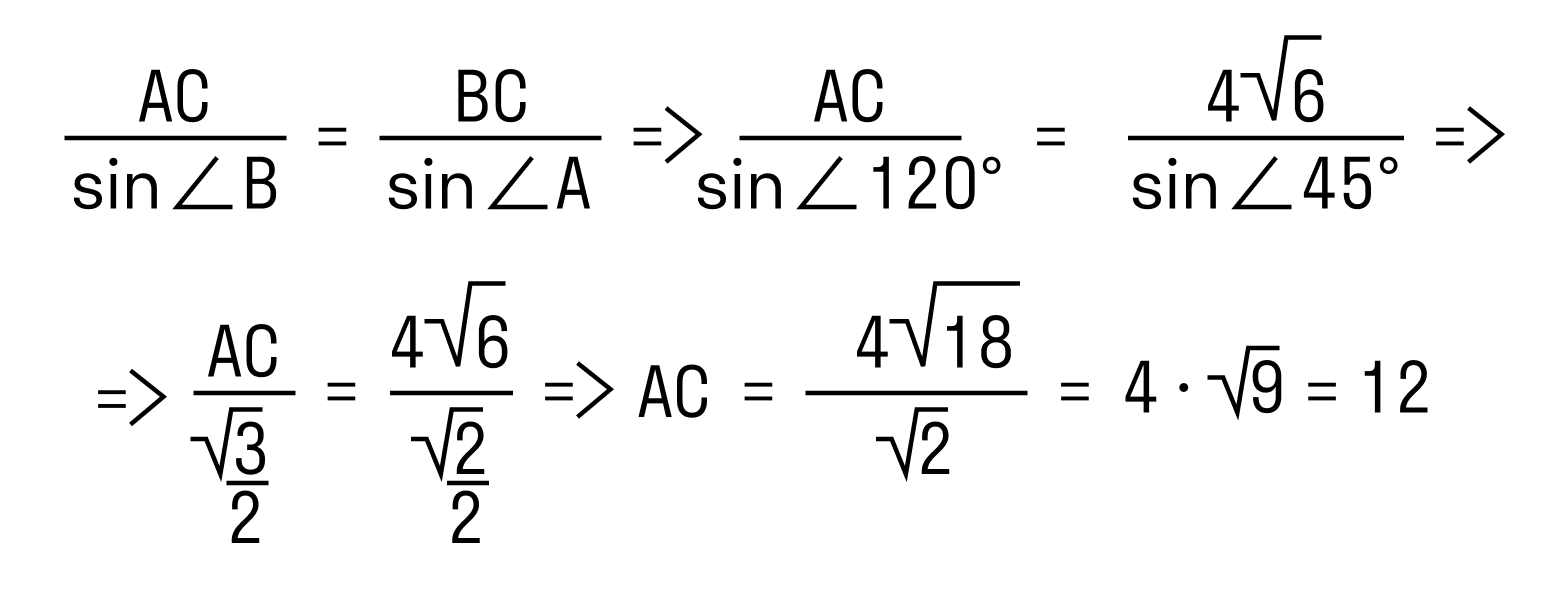
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так: