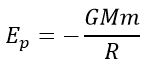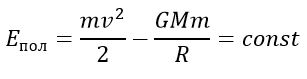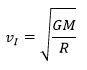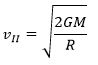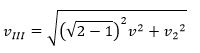Форма эллипса и степень его сходства с окружностью

В своё время, Кеплер на основании анализа наблюдений других учёных, Тихо Браге и Коперника, вывел три закона. Они дают описание гелиоцентрической орбиты планеты. Основу его соотношений составили опыт и эксперименты. Законы Кеплера являются важным инструментом в развитии астрономии.

Иоганн Кеплер

Считается, что погрешность Кеплеровых законов максимум 1%. Между тем, учёный не смог сам научно обосновать свои выводы. Более того, можно сказать, что выдвинул он их интуитивно.

Впоследствии данные предположения теоретически доказал Исаак Ньютон. Также в дальнейшем их применение было обоснованно классической механикой.

Бесспорно, работы ученого в значительной мере способствовали пониманию внутренней системы движения космических объектов.

Познавать означает сопоставлять воспринятое извне с внутренними идеями и выносить суждение о том, насколько то и другое совпадает.
Иоган Кеплер

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Первый закон Кеплера

Это эллипсический закон.
В нашей системе планеты осуществляют оборот по эллипсу. К тому же, Солнце находится на одном из фокусов данной кривой.
Форму эллипса и его сходство с окружностью определяют эксцентриситетом. Это выражение сечения конуса в числовой мере. Более того, именно он указывает на степень отклонения от окружности.
Его вычисляют делением промежутка от центра до фокуса эллипса на большую полуось. Если расстояние равно нулю, соответственно эллипс будет являться окружностью.

Первый закон Кеплера

Открытие и использование закона всемирного тяготения в астрономии является доказательством первого закона Кеплера.

Закон всемирного тяготения разработал Исаак Ньютон. Он установил, что каждый объект во Вселенной притягивает другой объект по определённой линии, которая соединяет центры их масс. Но в то же время является пропорциональной массе каждого объекта, и обратно пропорциональной квадрату расстояния между этими объектами.

Первый закон Кеплера взаимосвязан с ньютоновскими законами.
Во втором законе Ньютон утверждал и доказывал, что ускорение объекта является пропорциональной равнодействующей всех сил, которые прилагаются к объекту. Кроме того, ускорение также является обратно пропорциональным массе объекта.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Второй кеплеровский закон

По другому, его называют законом площадей. Он сообщает, что каждая планета движется в определённой плоскости, которая простирается через центр Солнца. Вдобавок радиус-вектор, объединяющий планету и Солнце, заметает собой равные площади за равные промежутки времени.

Второй закон Кеплера

В Солнечной системе планеты движутся вокруг Солнца совсем непостоянно. Например, от самой ближней точки орбиты до главной звезды наблюдается большая скорость, чем от самой дальней точки.

Действительно, мы наблюдаем такое явление в начале года. Видимое движение Солнца проходит быстрее, нежели в другое время. Так как Земля в это время расположена на ближнем пункте орбиты. Кстати, её называют перигелий. А прямо противоположную точку, то есть самую отдаленную-афелий.

Видео:Аналитическая геометрия: окружность и эллипсСкачать

Третий закон Кеплера

Часто его называют гармоничным законом. Он подразумевает, что период вращения планеты в квадрате вокруг Солнца относится, как куб большой полуоси орбиты планеты.

По правилам силы гравитации, закон Кеплера не совсем точен. Помимо всего прочего, в нём должна учитываться масса планеты.

Гармоничный закон с учётом закона тяготения актуально применять для измерения массы космического объекта. Но только, если установлены их орбиты.

Третий закон Кеплера

Третий закон Кеплера показывает связь между промежутком от планеты до звезды и периодом обращения по орбите. Проще говоря, чем планета ближе к Солнцу, тем быстрее она крутится.

Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Как применяют законы Кеплера

Законы движения планет в астрономии происходят по законам Кеплера. В них учёный даёт объяснение и определение неоднородного перемещения космических тел. Кроме того, благодаря этим законам стало возможным установление положения объектов. Более того, с их помощью можно рассчитать массу тел.

Интересно, что планеты Солнечной системы в большинстве имеют орбиты, приближенные к окружности. Хотя особая выпуклость характерна для Марса и Плутона.

Орбиты планет Солнечной системы

Очевидно, что законы движения планет равносильны правилам движения спутников. Кстати, даже искусственных. То есть то, что мы запускаем в космос движется по этим самым принципам.

Можно сделать вывод, что благодаря обладанию знаний о закономерностях движения, стал возможным запуск космических ракет. А значит, сделан огромный шаг в направлении изучения Вселенной.

Безусловно, Кеплер внёс огромный вклад в астрономию. Его во всех смыслах можно назвать удивительным человеком. В то время, когда он жил никто не представлял Вселенную так, как он. Более того, сам он писал о себе: Этому человеку на роду написано проводить время за решением трудных задач, отпугивающих других.

И ведь действительно, благодаря его труду сформировалась планетарная астрономия. Можно сказать, открылось окно во Вселенную. Где, то что мы видим, мы можем измерить.

Однако, изначально было опубликовано только два закона. Позднее, спустя десять лет, общественности стал доступен третий закон Кеплера.

Астрономия

Разумеется, не все догадки учёных умов верны. Но свой вклад они определённо внесли. Мы уже говорили о том, что за все время изучения астрономии было сделано множество важных открытий. Сегодня, я думаю, мы в очередной раз рассмотрели и убедились в этом.

Видео:Длина окружности. Математика 6 класс.Скачать

Потенциальная энергия взаимодействия двух тел

Пусть два тела с массами M и m находятся на расстоянии R друг от друга. Тогда энергия их взаимодействия равна

Видео:Видеоурок "Эллипс"Скачать

Полная энергия

Если тело находится в гравитационном поле и имеет некоторую скорость, то его полная энергия равна

Таким образом, в соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.

Теорема вириала

В случае кругового движения кинети­ческая энергия в 2 раза меньше по модулю потенциальной. Поэтому

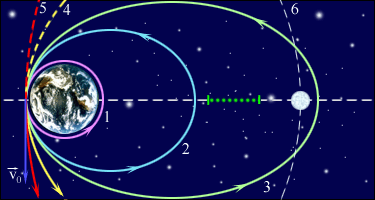
Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела.

При E_пол Система с отрицательной полной энергией называется гравитационно связанной .

При E_пол = 0 тело движется по параболической траектории. Скорость тела на бесконечности равна нулю.

При E_пол > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии.

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Первая космическая скорость

Это скорость движения по круговой траектории вблизи поверхности Земли

Это минимальная скорость, которую нужно сообщить телу, чтобы оно преодолело притяжение Земли и стало спутником. Для Земли примерно 7,9 км/с.

Видео:10 Окружность и эллипсСкачать

Вторая космическая скорость

Это скорость движения по параболической траектории

Она равна минимальной скорости, которую нужно сообщить телу на поверхности Земли, чтобы оно, преодолев земное притяжение, стало искусственным спутником Солнца . Находится из условия равенства нулю полной энергии системы. Для Земли примерно 11,2 км/с.

Видео:Оптическое свойство эллипса и его применение в медицинеСкачать

Третья космическая скорость

Это скорость, при которой тело преодолевает притяжение Солнца

где v – орбитальная скорость планеты, v ₂ – вторая космическая скорость для планеты. Для Земли примерно 16,6 км/с.

Задачи:

Звезда и планета обращаются вокруг общего неподвижного центра масс по круговым орбитам. Найдите массу планеты m, если известно, что скорость движения планеты равна v ₁ , а скорость движения и период обращения звезды равны v ₂ и T соответственно.

Если бы все линейные размеры Солнечной системы были пропорционально сокращены так, чтобы среднее расстояние между Солнцем и Землей стало 1 м, то какова была бы продолжительность одного года? Считайте, что плотность небесных тел при этом не меняется.

Автоматическая станция обращается вокруг планеты Марс с периодом T = 18 ч. Максимальное удаление от поверхности Марса (в апоцентре) a = 25000 км, минимальное (в перицентре) p = 1380 км. По указанным параметрам орбиты станции определите отношение массы Марса к массе Земли. Радиус Марса r_м = 3400 км, радиус Земли r_з = 6400 км.

Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты 422 тыс. км.

Вычислить параболическую скорость на поверхности Луны, R_Л = 0.27 радиуса Земли, M_Л = 1/81 массы Земли.

Видео:Как найти площадь эллипса, или почему современные дети не умеют думатьСкачать

Школьная Энциклопедия

Видео:ЭллипсСкачать

Nav view search

Navigation

Search

«Он жил в эпоху, когда ещё не было уверенности в существовании некоторой общей закономерности для всех явлений природы.

. Какой глубокой была у него вера в такую закономерность, если, работая в одиночестве, никем не поддерживаемый и не понятый, он на протяжении многих десятков лет черпал в ней силы для трудного и кропотливого эмпирического исследования движения планет и математических законов этого движения!

Сегодня, когда этот научный акт уже совершился, никто не может оценить полностью, сколько изобретательности, сколько тяжёлого труда и терпения понадобилось, чтобы открыть эти законы и столь точно их выразить» (Альберт Эйнштейн о Кеплере).

Иоганн Кеплер первым открыл закон движения планет Солнечной системы. Но сделал это он на основе анализа астрономических наблюдений Тихо Браге. Поэтому поговорим сначала о нем.

Видео:Изображение окружности в перспективе. Эллипс.Скачать

Тихо Браге (1546-1601)

Тихо Браге — датский астроном, астролог и алхимик эпохи Возрождения. Первым в Европе начал проводить систематические и высокоточные астрономические наблюдения, на основании которых Кеплер вывел законы движения планет.

Астрономией увлекся еще в детстве, вел самостоятельные наблюдения, создал некоторые астрономические инструменты. Однажды (11 ноября 1572 года), возвращаясь домой из химической лаборатории, он заметил в созвездии Кассиопеи необычайно яркую звезду, которой раньше не было. Он сразу понял, что это не планета, и бросился измерять её координаты. Звезда сияла на небе ещё 17 месяцев; вначале она была видна даже днём, но постепенно её блеск тускнел. Это была первая за 500 лет вспышка сверхновой в нашей Галактике. Событие это взбудоражило всю Европу, было множество истолкований этого «небесного знамения» — предсказывали катастрофы, войны, эпидемии и даже конец света. Появились и учёные трактаты, содержащие ошибочные утверждения о том, что это комета или атмосферное явление. В 1573 г. вышла первая его книга «О новой звезде». В ней Браге сообщал, что никакого параллакса (изменения видимого положения объекта относительно удалённого фона в зависимости от положения наблюдателя) у этого объекта не обнаружено, и это убедительно доказывает, что новое светило — звезда, и находится она не вблизи Земли, а по крайней мере на планетном расстоянии. С появлением этой книги Тихо Браге был признан первым астрономом Дании. В 1576 г. указом датско-норвежского короля Фредерика II Тихо Браге был пожалован в пожизненное пользование остров Вен (Hven), расположенный в 20 км от Копенгагена, а также выделены значительные суммы на постройку обсерватории и её содержание. Это было первое в Европе здание, специально построенное для астрономических наблюдений. Тихо Браге назвал свою обсерваторию «Ураниборг» в честь музы астрономии Урании (это название иногда переводят как «Небесный замок»). Проект здания составил сам Тихо Браге. В 1584 г. рядом с Ураниборгом был построен ещё один замок-обсерватория: Стьернеборг (в переводе с датского «Звёздный замок»). В скором времени Ураниборг стал лучшим в мире астрономическим центром, сочетавшим наблюдения, обучение студентов и издание научных трудов. Но в дальнейшем, в связи со сменой короля. Тихо Браге лишился финансовой поддержки, а затем последовало запрещение заниматься на острове астрономией и алхимией. Астроном покинул Данию и остановился в Праге.

Вскоре Ураниборг и все связанные с ним постройки были полностью разрушены (в наше время они частично восстановлены).

В это напряжённое время Браге пришёл к выводу, что ему нужен молодой талантливый помощник-математик для обработки накопленных за 20 лет данных. Узнав о гонениях на Иоганна Кеплера, незаурядные математические способности которого он уже успел оценить из их переписки, Тихо пригласил его к себе. Перед учеными стояла задача: вывести из наблюдений новую систему мира, которая должна прийти на смену как птолемеевской, так и коперниковой. Он поручил Кеплеру ключевую планету: Марс, движение которого решительно не укладывалось не только в схему Птолемея, но и в собственные модели Браге (по его расчётам, орбиты Марса и Солнца пересекались).

В 1601 г. Тихо Браге и Кеплер начали работу над новыми, уточнёнными астрономическими таблицами, которые в честь императора получили название «Рудольфовых»; они были закончены в 1627 г. и служили астрономам и морякам вплоть до начала XIX века. Но Тихо Браге успел только дать таблицам название. В октябре он неожиданно заболел и умер от неизвестной болезни.

Тщательно изучив данные Тихо Браге, Кеплер открыл законы движения планет.

Видео:#198. ЭЛЛИПС, ГИПЕРБОЛА, ПАРАБОЛАСкачать

Законы движения планет Кеплера

Первоначально Кеплер планировал стать протестантским священником, но благодаря незаурядным математическим способностям был приглашён в 1594 г. читать лекции по математике в университете города Граца (сейчас это Австрия). В Граце Кеплер провёл 6 лет. Здесь в 1596 г. вышла в свет его первая книга «Тайна мира». В ней Кеплер попытался найти тайную гармонию Вселенной, для чего сопоставил орбитам пяти известных тогда планет (сферу Земли он выделял особо) различные «платоновы тела» (правильные многогранники). Орбиту Сатурна он представил как круг (ещё не эллипс) на поверхности шара, описанного вокруг куба. В куб в свою очередь был вписан шар, который должен был представлять орбиту Юпитера. В этот шар был вписан тетраэдр, описанный вокруг шара, представлявшего орбиту Марса и т. д. Эта работа после дальнейших открытий Кеплера утратила своё первоначальное значение (хотя бы потому, что орбиты планет оказались не круговыми); тем не менее, в наличие скрытой математической гармонии Вселенной Кеплер верил до конца жизни, и в 1621 г. переиздал «Тайну мира», внеся в нее многочисленные изменения и дополнения.

Будучи великолепным наблюдателем, Тихо Браге за много лет составил объёмный труд по наблюдению планет и сотен звёзд, причём точность его измерений была существенно выше, чем у всех предшественников. Для повышения точности Браге применял как технические усовершенствования, так и специальную методику нейтрализации погрешностей наблюдения. Особо ценной была систематичность измерений.

На протяжении нескольких лет Кеплер внимательно изучает данные Браге и в результате тщательного анализа приходит к выводу, что траектория движения Марса представляет собой не круг, а эллипс, в одном из фокусов которого находится Солнце — положение, известное сегодня как первый закон Кеплера.

Первый закон Кеплера (закон эллипсов)

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

Форма эллипса и степень его сходства с окружностью характеризуется отношением , где — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), — большая полуось. Величина называется эксцентриситетом эллипса. При , и, следовательно , эллипс превращается в окружность.

Дальнейший анализ приводит ко второму закону. Радиус-вектор, соединяющий планету и Солнце, в равное время описывает равные площади. Это означало, что чем дальше планета от Солнца, тем медленнее она движется.

Второй закон Кеплера (закон площадей)

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

С этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

Третий закон Кеплера (гармонический закон)

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

, где и — периоды обращения двух планет вокруг Солнца, а и — длины больших полуосей их орбит.

Ньютон позднее установил, что третий закон Кеплера не совсем точен — в него входит и масса планеты: , где — масса Солнца, а и — массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Видео:7.1. Кривые второго порядка. Окружность. Эллипс. ГиперболаСкачать

Значение открытий Кеплера в астрономии

Открытые Кеплером три закона движения планет полностью и точно объяснили видимую неравномерность этих движений. Вместо многочисленных надуманных эпициклов модель Кеплера включает только одну кривую — эллипс. Второй закон установил, как меняется скорость планеты при удалении или приближении к Солнцу, а третий позволяет рассчитать эту скорость и период обращения вокруг Солнца.

Хотя исторически кеплеровская система мира основана на модели Коперника, фактически у них очень мало общего (только суточное вращение Земли). Исчезли круговые движения сфер, несущих на себе планеты, появилось понятие планетной орбиты. В системе Коперника Земля всё ещё занимала несколько особое положение, поскольку только у неё не было эпициклов. У Кеплера Земля — рядовая планета, движение которой подчинено общим трём законам. Все орбиты небесных тел — эллипсы, общим фокусом орбит является Солнце.

Кеплер вывел также «уравнение Кеплера», используемое в астрономии для определения положения небесных тел.

Законы, открытые Кеплером, послужили позже Ньютону основой для создания теории тяготения. Ньютон математически доказал, что все законы Кеплера являются следствиями закона тяготения.

Но в бесконечность Вселенной Кеплер не верил и в качестве аргумента предложил фотометрический парадокс (это название возникло позже): если число звёзд бесконечно, то в любом направлении взгляд наткнулся бы на звезду, и на небе не существовало бы тёмных участков. Кеплер, как и пифагорейцы, считал мир реализацией некоторой числовой гармонии, одновременно геометрической и музыкальной; раскрытие структуры этой гармонии дало бы ответы на самые глубокие вопросы.

Видео:4K Построение эллипса по точкам, ellipse constructionСкачать

Другие достижения Кеплера

В математике он нашёл способ определения объёмов разнообразных тел вращения, предложил первые элементы интегрального исчисления, подробно проанализировал симметрию снежинок, работы Кеплера в области симметрии нашли позже применение в кристаллографии и теории кодирования. Он составил одну из первых таблиц логарифмов, впервые ввёл важнейшее понятие бесконечно удалённой точки, ввёл понятие фокуса конического сечения и рассмотрел проективные преобразования конических сечений, в том числе меняющие их тип.

В физике ввёл термин инерция как прирождённое свойство тел сопротивляться приложенной внешней силе, вплотную подошёл к открытию закона тяготения, хотя и не пытался выразить его математически, первый, почти на сто лет раньше Ньютона, выдвинул гипотезу о том, что причиной приливов является воздействие Луны на верхние слои океанов.

В оптике: с его трудов начинается оптика как наука. Он описывает преломление света, рефракцию и понятие оптического изображения, общую теорию линз и их систем. Кеплер выяснил роль хрусталика, верно описал причины близорукости и дальнозоркости.

К астрологии у Кеплера было отношение двойственное. Приводят по этому поводу два его высказывания. Первое: «Конечно, эта астрология — глупая дочка, но, Боже мой, куда бы делась её мать, высокомудрая астрономия, если бы у неё не было глупенькой дочки! Свет ведь ещё гораздо глупее и так глуп, что для пользы этой старой разумной матери глупая дочка должна болтать и лгать. И жалованье математиков так ничтожно, что мать, наверное бы, голодала, если бы дочь ничего не зарабатывала». И второе: «Люди ошибаются, думая, что от небесных светил зависят земные дела». Но, тем не менее, Кеплер составлял гороскопы для себя и своих близких.

🎦 Видео

Эллипс | Элементы аналитической геометрииСкачать

11 класс, 52 урок, ЭллипсСкачать

Длина эллипса и разложение в ряд для эллиптического интегралаСкачать

Эллипс. Построение и параметры | Аналитическая геометрияСкачать

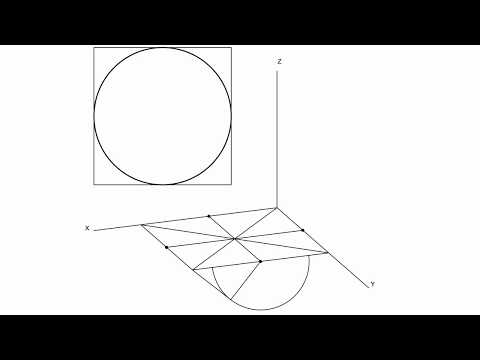
Построение эллипса по восьми точкам в прямоугольной диметрииСкачать