Евклидов треугольник с углами

Теорема Евклида: доказательство, применение и упражнения — Наука

Видео:IBLS — Существует ли треугольник, у которого все углы прямые? #shortsСкачать

Содержание:

В Теорема евклида демонстрирует свойства прямоугольного треугольника, рисуя линию, разделяющую его на два новых прямоугольных треугольника, которые похожи друг на друга и, в свою очередь, похожи на исходный треугольник; тогда возникает соотношение пропорциональности.

Евклид был одним из величайших математиков и геометров древности, выполнившим несколько доказательств важных теорем. Один из основных — тот, который носит его имя, получивший широкое распространение.

Это произошло потому, что с помощью этой теоремы она просто объясняет геометрические отношения, существующие в прямоугольном треугольнике, где его катеты связаны со своими проекциями в гипотенузу.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Формулы и демонстрация

Теорема Евклида предполагает, что в каждом прямоугольном треугольнике, когда рисуется линия — которая представляет высоту, которая соответствует вершине прямого угла относительно гипотенузы — два прямоугольных треугольника формируются из оригинала.

Эти треугольники будут похожи друг на друга, а также будут похожи на исходный треугольник, что означает, что их одинаковые стороны пропорциональны друг другу:

Углы трех треугольников равны; другими словами, когда они поворачиваются на 180 градусов вокруг своей вершины, один угол совпадает с другим. Это означает, что все они будут одинаковыми.

Таким образом, сходство, которое существует между тремя треугольниками, также может быть проверено благодаря равенству их углов. Из подобия треугольников Евклид устанавливает их пропорции с помощью двух теорем:

— Теорема о высоте.

— Теорема о ногах.

Эта теорема имеет широкое применение. В древние времена его использовали для вычисления высот или расстояний, что было большим достижением тригонометрии.

В настоящее время он применяется в различных областях, основанных на математике, таких как инженерия, физика, химия и астрономия, а также во многих других областях.

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Теорема о высоте

В этой теореме установлено, что в любом прямоугольном треугольнике высота, проведенная из прямого угла относительно гипотенузы, является геометрическим пропорциональным средним (квадрат высоты) между проекциями катетов, которые он определяет на гипотенузу.

То есть квадрат высоты будет равен произведению спроецированных катетов, образующих гипотенузу:

Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Демонстрация

Для треугольника ABC, который находится прямо в вершине C, при построении высоты образуются два похожих прямоугольных треугольника: ADC и BCD; следовательно, их соответствующие стороны пропорциональны:

Таким образом, чтобы высота h_c что соответствует отрезку CD, соответствует гипотенузе AB = c, поэтому имеем:

В свою очередь, это соответствует:

Решение гипотенузы (h_c), чтобы умножить два члена равенства, мы должны:

Таким образом, значение гипотенузы определяется как:

Видео:Площади треугольников с равным углом.Скачать

Теорема о ногах

В этой теореме установлено, что в каждом прямоугольном треугольнике мерой каждого катета будет среднее геометрическое пропорциональное (квадрат каждого катета) между мерой гипотенузы (полной) и проекцией каждого катета на нее:

Видео:В тупоугольном треугольнике все углы тупые. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Демонстрация

Дан треугольник ABC, который находится прямо в вершине C таким образом, что его гипотенуза равна c, при построении высоты (h) определяются проекции катетов a и b, которые являются отрезками m и n соответственно и лежат на гипотенуза.

Таким образом, высота, нарисованная на прямоугольном треугольнике ABC, образует два похожих прямоугольных треугольника, ADC и BCD, так что соответствующие стороны пропорциональны, например:

DB = n — проекция катета CB на гипотенузу.

AD = m, которая представляет собой проекцию катета AC на гипотенузу.

Тогда гипотенуза c определяется суммой катетов ее проекций:

Благодаря схожести треугольников ADC и BCD имеем:

Вышеупомянутое такое же, как:

Решая для ноги «а» умножить два члена равенства, мы имеем:

Таким образом, значение отрезка «а» определяется по формуле:

Таким же образом, благодаря схожести треугольников ACB и ADC, мы имеем:

Решив для ноги «b» умножить два члена равенства, мы имеем:

Таким образом, значение отрезка «b» определяется по формуле:

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Связь между теоремами Евклида

Теоремы, касающиеся высоты и катетов, связаны друг с другом, потому что оба измеряются относительно гипотенузы прямоугольного треугольника.

Через соотношение теорем Евклида можно также найти значение высоты; это возможно, решив значения m и n из теоремы о ногах, и они заменены в теореме о высоте. Таким образом проверяется, что высота равна произведению катетов, разделенных на гипотенузу:

В теореме о высоте заменим m и n:

час_c 2 = (b 2 ÷ c) _* (чтобы 2 ÷ c)

Видео:Треугольники с углами 45, 45 и 90 градусовСкачать

Решенные упражнения

Видео:7 класс, 33 урок, Теорема о соотношениях между сторонами и углами треугольникаСкачать

Пример 1

Дан треугольник ABC, прямо в точке A, определите размер AC и AD, если AB = 30 см и BD = 18 см.

Видео:🔥 ФОКУС с треугольником #shortsСкачать

Решение

В этом случае у нас есть измерения одной из спроецированных сторон (BD) и одной из сторон исходного треугольника (AB). Таким образом, можно применить теорему о ноге, чтобы найти значение ноги BC.

AB 2 = BD _* до н.э

Значение отрезка CD можно найти, зная, что BC = 50:

CD = 50 — 18 = 32 см

Теперь можно определить значение отрезка AC, снова применив теорему о ноге:

AC = √1600 = 40 см

Для определения значения высоты (AD) применяется теорема о высоте, поскольку значения проецируемых опор CD и BD известны:

ОБЪЯВЛЕНИЕ 2 = 32 _* 18

ОБЪЯВЛЕНИЕ 2 = 576

Видео:Геометрия Суровый челябинский челендж Задача Построить треугольник по периметру и двум угламСкачать

Пример 2

Определите значение высоты (h) треугольника MNL прямо в N, зная размеры отрезков:

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Решение

У нас есть размер одного из катетов, спроецированных на гипотенузу (PM), а также меры катетов исходного треугольника. Таким образом, мы можем применить теорему о ногах, чтобы найти значение другой спроецированной ноги (LN):

Поскольку значение катетов и гипотенузы уже известно, через взаимосвязь теорем о высоте и катетах можно определить значение высоты:

h = (b 2 _* к 2 ) ÷ c.

Видео:Задача, которую боятсяСкачать

Ссылки

1. Браун, Э. (2011). Хаос, фракталы и странности. Фонд экономической культуры.
2. Кабрера, В. М. (1974). Современная математика, Том 3.
3. Даниэль Эрнандес, Д. П. (2014). 3-й курс математики. Каракас: Сантильяна.
4. Энциклопедия Британника, я. (1995). Испанская энциклопедия: Macropedia. Энциклопедия Britannica Publishers.
5. Евклид, Р. П. (1886). Элементы геометрии Евклида.
6. Гуарденьо, А. Дж. (2000). Наследие математики: от Евклида до Ньютона, гении через свои книги. Севильский университет.

Битва при Сепеде (1820 г.): причины, развитие, последствия

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Формулы Евклида, демонстрация, применение и упражнения

Теорема Евклида демонстрирует свойства прямоугольного треугольника, рисуя линию, которая делит его на два новых прямоугольных треугольника, которые похожи друг на друга и, в свою очередь, похожи на исходный треугольник; то есть отношение пропорциональности.

Евклид был одним из величайших математиков и геометров древнего века, который сделал несколько демонстраций важных теорем. Одним из основных является тот, который носит его имя, который получил широкое применение.

Это было так, потому что, по этой теореме говорит просто существующие геометрические отношения в треугольнике, где ноги этого связаны с их проекциями на гипотенузе.

• 1 Формулы и демонстрация
  • 1.1 Теорема о высоте
  • 1.2 Теорема о ножках
• 2 Связь между теоремами Евклида
• 3 упражнения выполнены
  • 3.1 Пример 1
  • 3.2 Пример 2
• 4 Ссылки

Видео:Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Формулы и демонстрация

Теорема Евклида предполагает, что в каждом прямом треугольнике, когда рисуется линия, которая представляет высоту, соответствующую вершине прямого угла относительно гипотенузы, два прямоугольных треугольника образуются из оригинала..

Эти треугольники подобны друг другу, а также быть похож на оригинальный треугольник, а это значит, что их собратья стороны пропорциональны друг другу:

Углы трех треугольников совпадают; то есть, когда его вершина поворачивается на 180 градусов, угол совпадает с другой. Это подразумевает, что все будут равны.

Таким образом, вы также можете проверить сходство, которое существует между тремя треугольниками, по равенству их углов. Исходя из сходства треугольников, Евклид устанавливает их пропорции из двух теорем:

— Теорема о высоте.

— Теорема о ногах.

Эта теорема имеет широкое применение. В древности он использовался для расчета высоты или расстояния, что представляет собой большой прогресс для тригонометрии.

В настоящее время он применяется в нескольких областях, основанных на математике, таких как инженерия, физика, химия и астрономия, а также во многих других областях..

Теорема о высоте

Эта теорема утверждает, что в любом прямоугольном треугольнике высота, оттянутая под прямым углом относительно гипотенузы, является геометрическим пропорциональным средним (квадрат высоты) между проекциями ног, которые определяют гипотенузу..

То есть квадрат высоты будет равен умножению спроецированных ног, образующих гипотенузу:

шоу

Так, это прямоугольник в вершине C, чтобы составить треугольник АВС два подобных треугольника, генерируются АЦП и BCD; Поэтому, их соответствующие стороны пропорциональны:

Таким образом, что высота h_с который соответствует сегменту CD, соответствует гипотенузе AB = c, поэтому необходимо:

В свою очередь это соответствует:

Очистка гипотенузы (ч_с), чтобы умножить два члена равенства, вы должны:

Таким образом, значение гипотенузы определяется как:

Теорема о ногах

Эта теорема утверждает, что в любом прямоугольном треугольнике мера каждой ноги будет средним геометрическим пропорциональным (квадрат каждой ноги) между измерением гипотенузы (завершено) и проекцией каждого на нее:

шоу

Для данного треугольника ABC, который является прямоугольником в вершине C, так что его гипотенуза равна c, при построении высоты (h) определяются проекции ножек a и b, которые являются отрезками m и n соответственно. гипотенуза.

Таким образом, высота должна быть обращена на треугольнике АВС генерирует два одинаковых прямоугольников, треугольники ADC и BCD, так что соответствующие стороны пропорциональны, а также:

DB = n, который является проекцией ноги CB на гипотенузу.

AD = m, которая является проекцией катетера AC на гипотенузу.

Тогда гипотенуза c определяется по сумме ножек ее проекций:

Из-за сходства треугольников ADC и BCD нам необходимо:

Вышеуказанное совпадает с:

Очистив ногу «а», чтобы умножить два члена равенства, нужно:

Таким образом, значение ноги «а» определяется как:

Аналогично, по сходству треугольников ACB и ADC мы должны:

Очистив ногу «b», чтобы умножить два члена равенства, нужно:

Таким образом, значение ноги «b» определяется как:

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Связь между теоремами Евклида

Теоремы со ссылкой на высоту и ноги взаимосвязаны, потому что измерение выполняются как для гипотенузы треугольника.

С помощью соотношения теорем Евклида значение высоты также может быть найдено; это возможно путем очистки значений m и n из теоремы о ножке, и они заменяются в теореме о высоте. Таким образом, высота равна умножению ног, разделенному на гипотенузу:

В теореме о высоте m и n заменены:

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Решенные упражнения

Пример 1

Учитывая треугольник ABC, прямоугольник в A, определите меру AC и AD, если AB = 30 см и BD = 18 см.

решение

В этом случае у нас есть измерения одной из спроектированных ног (BD) и одной из ног исходного треугольника (AB). Таким образом, вы можете применить теорему ноги, чтобы найти значение ноги BC.

AB 2 = BD _* до нашей эры

(30) 2 = 18 _* до нашей эры

900 = 18 _* до нашей эры

Значение CD катетуса может быть найдено, зная, что BC = 50:

CD = 50 — 18 = 32 см

Теперь можно определить значение AC катета, снова применив теорему о ноге:

переменный ток 2 = CD _* BD

переменный ток 2 = 32 _* 50

переменный ток 2 = 160

AC = √1600 = 40 см

Для определения значения высоты (AD) применяется теорема о высоте, поскольку известны значения спроецированных ножек CD и BD:

нашей эры 2 = 32 _* 18

нашей эры 2 = 576

Пример 2

Определите значение высоты (h) треугольника MNL, прямоугольника в N, зная размеры сегментов:

решение

У вас есть измерение одной из ног, спроецированных на гипотенузу (PM), а также измерения ног исходного треугольника. Таким образом, теорема ноги может быть применена, чтобы найти значение другой спроектированной ноги (LN):

NL 2 = Вечера _* LM

По мере того как значение ног и гипотенузы, как известно, через соотношение высоты теоремы и ноги можно определить значение высоты:

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Пятый постулат Евклида, попытки его доказательства. Эквиваленты пятого постулата. Аксиоматика Гильберта. Следствия из аксиом Гильберта. Абсолютная геометрия. Аксиоматика Вейля.

В абсолютной геометрии (без использования пятого постулата) можно доказать: признаки равенства треугольника; в равнобедренном треугольнике углы при основании равны; теорему о внешнем угле треугольника: каждый из внешних углов треугольника больше любого внутреннего, с ним не смежного.

Доказательство (по Евклиду)

1. . Тогда треугольник равняется треугольнику (по двум сторонам и углу между ними), следовательно, . Но угол составляет часть внешнего угла при вершине . Значит, теорема доказана.

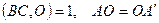
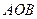
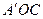
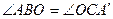
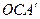
Последний момент (что угол 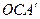составляет часть внешнего угла) устанавливается из наглядности чертежа, т.к. аксиомы Евклида не дают возможности точно обосновать понятия «между», «внутри» и т.д. Кроме того, в доказательстве использовалось понятие равенства треугольников, которое не обосновано, т.к. не определено движение у Евклида. Таким образом, приведенные рассуждения существенно подкрепляются наглядностью чертежа.

Пользуясь теоремой о внешнем угле треугольника без помощи пятого постулата легко доказывается следующая лемма: если при пересечении двух прямых секущей накрест лежащие углы (или соответственные углы) равны, то прямые не пересекаются.

Пусть при пересечении прямых и секущей АВ накрест лежащие углы равны (например, ). Допустим, что прямые и пересекаются в некоторой точке , то получим треугольник , у которого один из углов при вершине или равен внешнему, что противоречит теореме о внешнем угле. Второе утверждение следует непосредственно из доказанного.

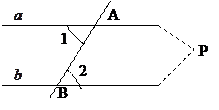
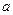
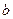
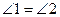
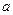
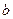
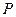
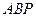
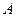
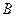
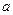
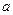
Пользуясь данной леммой, легко доказывается (без использования пятого постулата), что через каждую точку М, не лежащую на прямой , проходит прямая, параллельная прямой .

Возникает вопрос: сколько же прямых, параллельных прямой 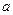, проходит через точку М. Ответ на этот вопрос дает следующая теорема: если имеет место пятый постулат, то через каждую точку М, не лежащую на прямой , проходит только одна прямая, параллельная прямой .

1. Проведем прямую , перпендикулярную к прямой , и прямую , проходящую через точку перпендикулярно к прямой . Тогда прямые и параллельны.

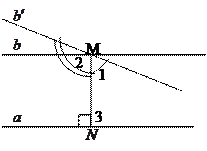
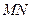
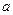
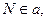
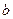
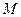
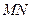
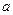
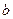
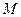
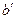
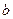
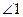
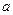
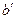
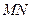
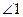
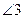
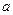
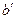
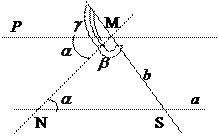
2. Проведем через точку произвольную прямую , отличную от прямой . Один из смежных углов (1 или 2) острый (пусть ). При пересечении прямых и с прямой получаем внутренние односторонние углы: и , сумма которых меньше двух прямых углов, значит по пятому постулату прямые и пересекаются.

Докажем обратную теорему: если принять, что через точку, не лежащую на данной прямой, проходит одна прямая, параллельная данной, то справедлив пятый постулат.

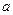
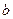
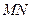
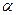
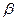
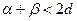
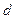
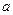
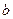
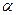
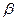
1. Пусть при пересечении прямых и секущей образованы внутренние односторонние углы и так, что , где — мера прямого угла. Докажем, что прямые и пересекаются в некоторой точке, лежащей в полуплоскости, в которой лежат углы и .

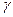
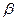
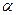
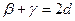
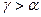
2. Обозначим через угол смежный с углом и накрест лежащий с углом . Так как , то из 1) следует, что .

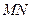
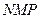
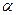
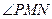
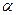
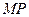
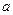
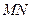
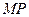
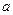
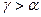
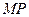
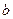
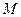
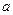
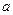
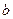
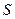
3. Отложим от луча угол , равный углу , так, чтобы и были накрест лежащими углами при пересечении прямых и прямой . По лемме прямые и параллельны. В силу неравенства прямые и не совпадают. Так как через точку проходит только одна прямая, параллельная прямой , то прямые и пересекаются в некоторой точке .

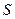
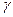
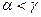
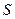
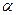
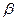
4. Если предположить, что точка лежит в той полуплоскости, в которой лежит угол , то в силу неравенства придем к противоречию с теоремой о внешнем угле треугольника. Таким образом, — точка той полуплоскости, в которой лежат углы и .

Итак, пятый постулат эквивалентен (равносилен) так называемой аксиоме параллельности прямых: через точку, не лежащую на данной прямой, проходит не более чем одна прямая, параллельная данной.

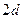
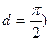
Итак, 5 постулату (если две прямые при пересечении с третьей образуют с одной стороны внутренние односторонние углы, сумма которых меньше , то эти прямые пересекаются при их достаточном продолжении с этой стороны. ( ) в Евклидовой геометрии отводится особое место.

На нем основана теория параллельных прямых, подобие фигур, теорема о сумме углов в треугольнике, теорема о сумме углов выпуклых многоугольников, тригонометрия, теория площадей и объемов. Попытки доказательства пятого постулата привели к признаку параллельности прямых, аксиом существования параллельной прямой. Пятый постулат также эквивалентен (равносилен) следующим утверждениям.

1. Сумма углов каждого треугольника равна двум прямым;

2. Существует хотя бы один треугольник, сумма углов которого равна 2d (d- прямой угол);

3. существует прямоугольник;

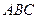
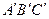
4. Существует пара треугольников и с равными углами;

5. Теорема Пифагора.

Со времен Евклида и до конца 19 века было множество попыток доказать 5-ый постулат (О.Хойям 1048-1023 г., Лежандр – 1750-1833 г и др.). Обычно автор доказательства незаметно для себя опирался на некоторое допущение, которое оказывалось еще одним эквивалентов 5-го постуоата. Попытки были бесплодными, но был получен ряд верных результатов, наиболее четкое доказательство которых было дано Лежандром.

Со времен Евклида также не прекращались попытки уточнять основные положения геометрии. Однако на протяжении многих веков к обоснованию геометрии никто не прибавил ничего принципиально нового сверх того, что уже было сделано Евклидом. Строгость евклидовых доказательств до 19 века казалась достаточной. Только в конце 19 века оформились воззрения на принципы логического построения геометрии.

В 1899 году вышла в свет книга Д. Гильберта «Основания геометрии». В ней впервые был дан список аксиом, достаточный для логического построения евклидовой геометрии. Полные списки аксиом евклидовой геометрии составлялись и до Гильберта, но не такие совершенные.

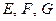
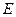
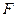
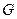
По Гильберту, база структуры евклидова пространства состоит из трех множеств: . — множество точек, — множество прямых, — множество плоскостей.

На этих множествах заданы 3 отношения: бинарное «принадлежит»; тернарное «лежит между»; бинарное «равно», которые удовлетворяют 20 аксиомам, разбитым на пять групп.

I группа- аксиомы принадлежности:

I₁ — каковы бы ни были две точки А и В существует прямая, проходящая через эти точки;

I₂ — каковы бы ни были две точки А и В существует не более одной прямой, проходящей через эти точки.

I₃ – на каждой прямой лежат по крайней мере две точки. Существует по крайней три точки, не лежащие на одной прямой.

I₄ – каковы бы ни были три точки, не лежащие на одной прямой, существует плоскость α, проходящая через эти точки. На каждой плоскости лежит хотя бы одна точка.

I₅ – каковы бы ни были три точки, не лежащие на одной прямой, существует не более одной плоскости, проходящей через эти точки.

I₆ – если две точки А и В прямой а, лежат в плоскости α, то каждая точка прямой а лежит в плоскости α.

I₇ – если две плоскости α и β имеют точку А, то плоскости имеют по крайней мере ёще одну любую точку В.

I₈ – существует по крайней мере четыре точки, не лежащие в одной плоскости.

С помощью этой группы доказываются теоремы:

1. Две прямые имеют не более одной точки пересечения.

2. Если две плоскости имеют одну общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

3. Через прямую и не лежащую на не точку так же как из двух пересекающихся прямых проходит одна и только одна плоскость.

4. На каждой плоскости существует 3 точки, не лежащие на одной прямой.

II группа аксиомы порядка:

II₁ – если точки А-В-С, то они являются разными точками одной прямой и точка В лежит между С и А.

II₂ – каковы бы ни были точки А и В существует не более одной точки, лежащей между другими.

II₃ –среди любых трех точек прямой, одна и только одна лежит между двумя другими.

II₄ – (аксиома Паша): Пусть А,В,С три точки, не лежащие на одной прямой, а— прямая в плоскости АВС, не проходящая ни через одну из них, тогда если прямая а проходит через точку отрезка АВ, то она также проходит через точки отрезка АС или ВС.

Дата добавления: 2017-01-29 ; просмотров: 3717 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

🔍 Видео

План полёта треугольника с углами по 90 градусов.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать