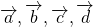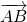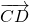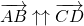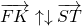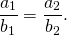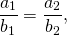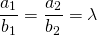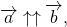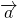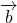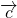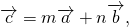Есть ли в треугольнике коллинеарные векторы

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Коллинеарные векторы

В данной публикации мы рассмотрим, какие векторы называются коллинеарными и перечислим условия, при которых они являются таковыми. Также разберем примеры решения задач по этой теме.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Условия коллинеарности векторов

Векторы, лежащие на одной или нескольких параллельных прямых, называются коллинеарными.

Два вектора коллинеарны, если выполняется одно из условий ниже:

1. Существует такое число n, при котором .

2. Отношения координат векторов равны. Но данное условие не может применяться, если одна из координат равняется нулю.

3. Векторное произведение равно нулевому вектору (применимо только для трехмерных задач).

Видео:Коллинеарные векторы.Скачать

Примеры задач

Задание 1
Даны векторы , и . Определим, есть ли среди них коллинеарные.

Решение:
У заданных векторов нет нулевых координат, значит мы можем применить второе условие коллинеарности.

Следовательно, коллинеарными являются только векторы a и c .

Задание 2
Выясним, при каком значении n векторы и коллинеарны.

Решение:
Т.к. среди координат нет нулей, согласно второму условию мы можем составить их соотношение, чтобы рассчитать недостающий элемент.

Видео:Вычитание векторов. 9 класс.Скачать

Коллинеарные векторы

Какие векторы называются коллинеарными?

Какими свойствами обладают коллинеарные векторы?

Векторы называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых.

Например, все векторы

коллинеарны между собой.

Нулевой вектор считают коллинеарным любому вектору.

Коллинеарные векторы делятся на сонаправленные и противоположно направленные.

Векторы

называются сонаправленными (или одинаково направленными), если лучи AB и CD сонаправлены.

(Сонаправленность векторов записывают с помощью знака ↑↑).

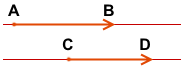
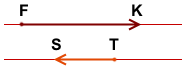
Векторы

называются противоположно направленными, если лучи AB и CD противоположно направлены.

(Противоположное направление векторов обозначают знаком ↑↓).

(Свойство коллинеарных векторов)

У коллинеарных векторов соответствующие координаты пропорциональны

То есть если векторы

(Признак коллинеарных векторов)

Если соответствующие координаты векторов пропорциональны, то эти векторы коллинеарны.

при λ>0 векторы сонаправлены

при λ

неколлинеарны, то любой вектор

можно разложить как

где m и n — некоторые числа.

Такое разложение единственно.

Видео:Понятие вектора. Коллинеарные векторы.Скачать

Операции над векторами и их свойства: сложение и умножение

Прежде чем приступить к тематике статьи, напомним основные понятия.

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Видео:Сложение коллинеарных векторовСкачать

Сложение двух векторов

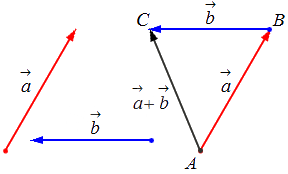
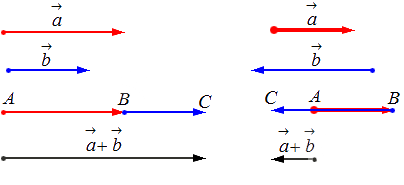
Исходные данные: векторы a → и b → . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор A B → , равный вектору а → ; из полученной точки undefined – вектор В С → , равный вектору b → . Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.

Геометрически сложение векторов выглядит так:

— для неколлинеарных векторов:

— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

Видео:Вектор. Определение. Коллинеарные векторы. Равные векторы.Скачать

Сложение нескольких векторов

Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

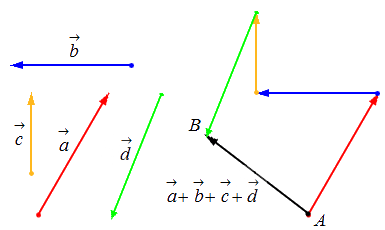
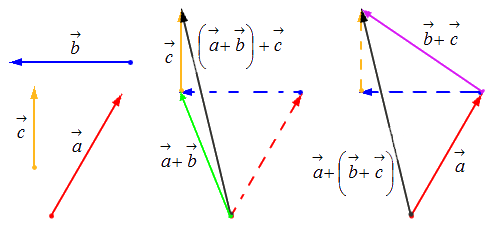
Исходные данные: векторы a → , b → , c → , d → . Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a → ; затем от конца полученного вектора откладывается вектор, равный вектору b → ; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B , а полученный отрезок (вектор) A B → – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .

Геометрически оно выглядит следующим образом:

Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a → и b → есть сумма векторов a → и — b → .

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Умножение вектора на число

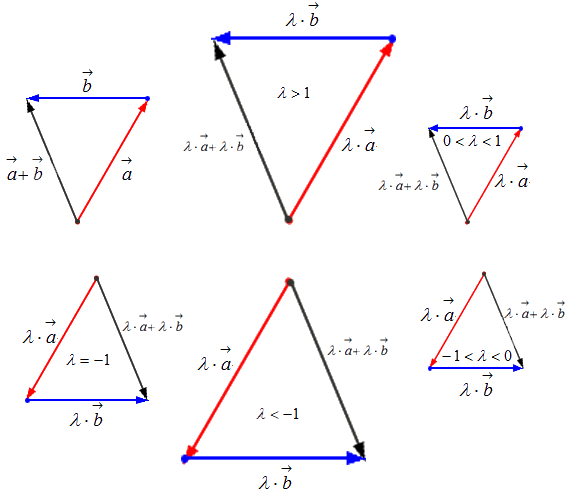
Чтобы произвести действие умножения вектора на некое число k , необходимо учитывать следующие правила:
— если k > 1 , то это число приведет к растяжению вектора в k раз;
— если 0 k 1 , то это число приведет к сжатию вектора в 1 k раз;
— если k 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k = 1 , то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.

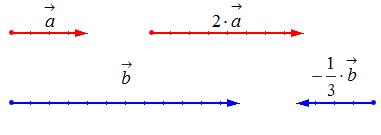
Исходные данные:
1) вектор a → и число k = 2 ;
2) вектор b → и число k = — 1 3 .

Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Видео:43. Компланарные векторыСкачать

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Исходные данные: векторы a → , b → , c → и произвольные действительные числа λ и μ .

1. Свойство коммутативности: a ⇀ + b → = b → + a → .
   
2. Свойство ассоциативности: ( a → + b → ) + c → = a → + ( b → + c → ) .
   
3. Свойство использования нейтрального элемента по сложению (нулевой вектор 0 → ⃗). Это очевидное свойство: a → + 0 → = a →
4. Свойство использования нейтрального элемента по умножению (число, равное единице): 1 · a → = a → . Это очевидное свойство, не предполагающее никаких геометрических преобразований.
5. Любой ненулевой вектор a → имеет противоположный вектор — a → и верным является равенство: a → + ( — a → ) = 0 → . Указанное свойство — очевидное.
6. Сочетательное свойство операции умножения: ( λ · µ ) · a → = λ · ( µ · a → ) . Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
7. Первое распределительное свойство (очевидно): ( λ + µ ) · a → = λ · a → + µ · a → .
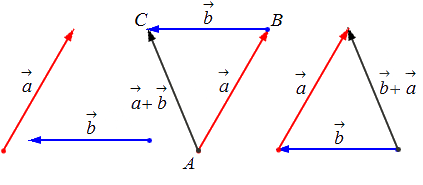
8. Второе распределительное свойство: λ · ( a → + b → ) = λ · a → + λ · b → .
   Геометрически это свойство определяется подобием треугольников:
   

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Задача: упростить выражение a → — 2 · ( b → + 3 · a → )
Решение
— используя второе распределительное свойство, получим: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · ( 3 · a → )
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a → — 2 · b → — 2 · ( 3 · a → ) = a → — 2 · b → — ( 2 · 3 ) · a → = a → — 2 · b → — 6 · a →
— используя свойство коммутативности, меняем местами слагаемые: a → — 2 · b → — 6 · a → = a → — 6 · a → — 2 · b →
— затем по первому распределительному свойству получаем: a → — 6 · a → — 2 · b → = ( 1 — 6 ) · a → — 2 · b → = — 5 · a → — 2 · b → Краткая запись решения будет выглядеть так: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · 3 · a → = 5 · a → — 2 · b →
Ответ: a → — 2 · ( b → + 3 · a → ) = — 5 · a → — 2 · b →

Видео:Коллинеарность векторовСкачать

Основные сведения о коллинеарных векторах — свойства координат

Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

Общие сведения

Изучать векторную алгебру начинают на уроках геометрии в средней школе (7 – 9 классы).

Вектор — это отрезок заданной длины и имеющий определенное направление.

С векторами можно выполнять различные математические операции: сложение, вычитание, умножение вектора на число и т. д.

Остановимся на операции умножения вектора на число. Пусть имеется вектор a → , умножим его на некоторое число k. Получим новый вектор b → = k · a → . Векторы a → и b → параллельны и направлены в одну сторону, отличие между ними заключается лишь в длине. Тогда данные векторы можно считать коллинеарными.

Коллинеарностью называется характеристика положения векторов, при котором векторы расположены на одной прямой или на параллельных прямых.

Видео:Сложение векторов. 9 класс.Скачать

Понятие коллинеарности векторов

Из определения следует, что понятие коллинеарный является синонимом понятию параллельный.

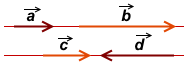
Векторы могут быть направлены в одну сторону или же в противоположные. Существует следующее правило для обозначения сонаправленных векторов b → и d → — b → ↑ ↑ d → и противоположно направленных — b → ↑ ↓ d → .

Узнать, являются ли векторы b → ( b 1 ; b 2 ) и d → ( d 1 ; d 2 ) коллинеарными, можно, проверив соблюдение одного из следующих условий:

1. b → и d → — пара коллинеарных векторов, если можно найти такое число λ, что b → = λ · d → . Это условие называют леммой о коллинеарности векторов. Докажем ее. Рассмотрим случай, когда b → ↑ ↑ d → . Тогда число λ = b → d → . Векторы являются сонаправленными, так как λ>0. Из условия равенства длин векторов, получим λ · d → = λ · d → = b → d → · d → = b → , что и требовалось доказать. Случай, когда b → ↑ ↓ d → , доказывается аналогично. Возьмем λ = — b → d → , чтобы получить сонаправленные векторы b → и d → . Тогда λ · d → = λ · d → = — b → d → · d → = b → . Лемма доказана. Чтобы понять, являются ли векторы сонаправленными, нужно определить знак λ. Если λ>0, направления векторов совпадают, иначе — не совпадают.
2. b → и d → — пара коллинеарных векторов, если соотношения их координат равны между собой: b 1 d 1 = b 2 d 2 . Способ применяется для векторов, среди координат которых нет нулей. Отметим, что данное условие идентично условию параллельности прямых, заданных каноническими уравнениями.

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Теорема о разложении векторов

Пусть на плоскости имеются три вектора b → , d → , c → . Тогда, если вектор d → выражается через b → и с → , говорят, что d → можно разложить по b → и c → . При этом вектор d → может быть как коллинеарным с одним из векторов, так и нет.

Сформулируем теорему о разложении векторов.

Любой вектор d → на плоскости можно представить в виде d → = x c → + y b → . При этом c → и b → — пара не коллинеарных векторов, и b → ≠ 0 , c → ≠ 0 . Такое представление называют разложением вектора.

Предположим, что d → коллинеарен b → .

Тогда согласно лемме: d → = y b → . Коэффициент x будет равным нулю, то есть d → = 0 · c → + y b → . Вектор разложен по векторам c → и b → . Теорема доказана.

В пространстве три вектора, два из которых коллинеарны, будут являться компланарными.

Рассмотрим случай, когда среди векторов d → , c → и b → нет коллинеарных.

На плоскости выберем точку M, из которой отложим отрезки M C → = c → , M D → = d → , M B = b → . Из точки D проведем прямую DC1||BM. Вектор d → можно найти по правилу треугольника, то есть d → = М С 1 → + D C 1 → .

D C 1 → и b → — пара коллинеарных векторов, так как лежат на параллельных прямых. Векторы M C 1 → и c → коллинеарны, поскольку лежат на одной прямой. Согласно лемме, D C 1 → = y · b → и M C 1 → = x · c → . Тогда d → = x · c → + y · b → , что и требовалось доказать.

Приведем доказательство, что x и y — однозначно определяемые коэффициенты. Предположим, что существуют x1 и y1, и d → = x 1 · c → + y 1 · b → . Получим, что x · c → + y · b → = x 1 · c → + y 1 · b → , или ( x — x 1 ) · c → + ( y — y 1 ) · b → = 0 .

По условию b → ≠ 0 и c → ≠ 0 , значит, равенство выполнимо только если x — x 1 = 0 и y — y 1 = 0 .

Тогда x = x 1 и y = y 1 , то есть x и y — единственно возможные коэффициенты разложения вектора d → .

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Признаки и свойства коллинеарности векторов

Коллинеарные векторы на плоскости или в пространстве обладают следующими свойствами:

• каждый вектор коллинеарен самому себе b → ↑ ↑ d → ;
• если вектор b → коллинеарен вектору d → , то справедливо обратное утверждение: вектор d → коллинеарен вектору b → ( b → ↑ ↑ d → ⇔ d → ↑ ↑ b → ) ;
• если ненулевой вектор b → коллинеарен ненулевому d → , а d → коллинеарен ненулевому c → , т о b → коллинеарен c → ;
• нулевой вектор коллинеарен любому другому. Нулевым вектор называют вектор, длина которого равна нулю, а начальная и конечная точки совпадают;
• скалярное произведение коллинеарных векторов b → и d → можно вычислить по формулам: b → ↑ ↑ d → ⇒ ( b → · d → ) = b → · d → и b → ↑ ↓ d → ⇒ ( b → · d → ) = — b → · d → .

Видео:№754. Начертите попарно неколлинеарные векторы х, у , z и постройте векторы x+у, x+z, z+y.Скачать

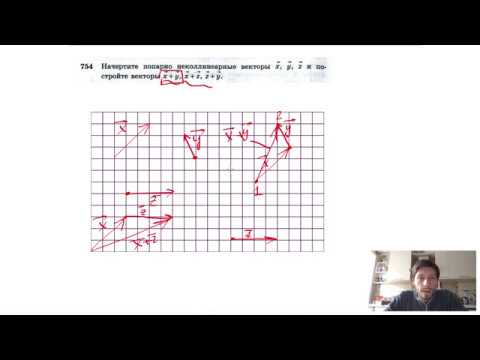
Примеры задач на коллинеарность векторов на плоскости

Определить, являются ли векторы f → ( 4 ; 10 ) и s → ( 2 ; 5 ) коллинеарными.

У векторов нет нулевых координат, проверим соблюдение условия коллинеарности векторов.

Для этого запишем отношения соответствующих координат по форме f 1 s 1 = f 2 s 2 .

Получим: 4 2 = 10 5 .

Ответ: векторы коллинеарные.

Даны три вектора с → ( 1 ; — 2 ) , b → ( 2 , x ) и d → ( 2 ; 2 ) , при этом с → и b → перпендикулярные.

Найти неизвестную координату x. Найти такое число α, при котором b → и d → будут коллинеарными.

Решение. Скалярное произведение перпендикулярных векторов равно нулю. Отсюда найдем неизвестную координату x:

c 1 b 1 + c 2 x = 0 ;

Запишем соотношения координат b → и d → , подставив найденное значение координаты х ( 1 ) :

b 1 d 1 = b 2 d 2 ⇔ 1 2 = 1 2 .

Как видно соотношения координат одинаковы при любом α ∈ R , где R – область действительных чисел.

Ответ: b → и d → коллинеарны при любом α ∈ R .

Дано два вектора d → = 3 , b → = 6 . Найти такое число α, чтобы зависимость вида d → = α b → отображала:

• коллинеарные сонаправленные векторы;
• коллинеарные противоположно направленные векторы.

Решение. Если векторы сонаправлены, то α>0. Получим: 3=6α. Откуда: α=0,5.

Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Коллинеарные векторы

Какие векторы называются коллинеарными?

Какими свойствами обладают коллинеарные векторы?

Векторы называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых.

Например, все векторы

коллинеарны между собой.

Нулевой вектор считают коллинеарным любому вектору.

Коллинеарные векторы делятся на сонаправленные и противоположно направленные.

Векторы

называются сонаправленными (или одинаково направленными), если лучи AB и CD сонаправлены.

(Сонаправленность векторов записывают с помощью знака ↑↑).

Векторы

называются противоположно направленными, если лучи AB и CD противоположно направлены.

(Противоположное направление векторов обозначают знаком ↑↓).

(Свойство коллинеарных векторов)

У коллинеарных векторов соответствующие координаты пропорциональны

То есть если векторы

(Признак коллинеарных векторов)

Если соответствующие координаты векторов пропорциональны, то эти векторы коллинеарны.

при λ>0 векторы сонаправлены

при λ

неколлинеарны, то любой вектор

можно разложить как

где m и n — некоторые числа.

Такое разложение единственно.

💡 Видео

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Угол между векторами. 9 класс.Скачать

10 класс, 43 урок, Компланарные векторыСкачать