Если все вершины многоугольника лежат на окружности то окружность называется (4 видео)

Геометрия. 8 класс

Введем новое понятие: описанная окружность.
Определение: если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

На рисунке четырёхугольник MNKP вписан в окружность с центром O, так как все его вершины лежат на этой окружности.

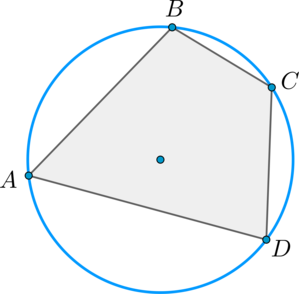
На рисунке четырёхугольник ABCD не является вписанным в окружность, т.к. вершина C не лежит на окружности.
Рассмотрим треугольник АВС и впишем его в окружность. Всегда ли это возможно сделать?

Докажем теорему: Около любого треугольника можно описать окружность.
Дано: ∆ABC
Доказать: существует окружность, что A, B, C принадлежат этой окружности.
Доказательство:
Построим в треугольнике серединные перпендикуляры к сторонам и обозначим точку их пересечения О.

По свойству серединных перпендикуляров точка О равноудалена от точек А, В и С, т.е. OA = OB = OC.

Поэтому окружность с центром в точке О и радиусом ОА проходит через все три вершины треугольника, а значит является описанной около треугольника АВС.
Треугольник ABC вписан в окружность с центром O.
Что и требовалось доказать.
Четырехугольник, вокруг которого можно описать окружность обладает свойством: в любом вписанном четырёхугольнике сумма противоположных углов равна 180°.

Дано: ABCD вписанный четырехугольник.
Доказать:
∠B + ∠D = 180° и ∠A + ∠C = 180°.
Доказательство:
Рассмотрим вписанный угол АВС. Его градусная мера равна ∠ABC = 0,5 ∙ ∪ADC.
Градусная мера вписанного угла ADC равна ∠ADC = 0,5 ∙ ∪ABC.
Сумма углов АВС и ADC равна
∠ABC + ∠ADC = 0,5(∪ADC + ∪ABC) = 0,5 ∙ 360° = 180°.
Что и требовалось доказать.
Обратное утверждение также верно. Докажите его самостоятельно:
Если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность.
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.

Содержание

Описанная окружность
Доказательство
Доказательство
Доказательство
Доказательство
Доказательство
Окружность: описанная около многоугольника
🎦 Видео

Видео:110. Окружность, описанная около правильного многоугольникаСкачать

Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Около любого треугольника можно описать окружность.

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Около треугольника можно описать только одну окружность.

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Около четырехугольника не всегда можно описать окружность.

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 .

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность.

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

Видео:Геометрия 8 класс (Урок№33 - Описанная окружность.)Скачать

Окружность: описанная около многоугольника

Определение

Окружность (S) описана около многоугольника (P) , если все вершины многоугольника (P) лежат на окружности (S) .

В этом случае многоугольник (P) называется вписанным в окружность.

Определение

Серединный перпендикуляр к отрезку – это прямая, проходящая через середину данного отрезка перпендикулярно ему.

Теорема

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Доказательство

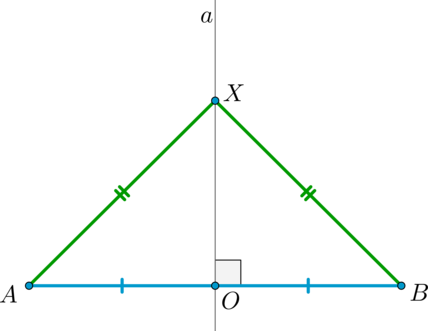
Рассмотрим отрезок (AB) и серединный перпендикуляр (a) к нему. Докажем, что для любой точки (Xin a) выполнено: (AX=BX) .

Рассмотрим (triangle AXB) : отрезок (XO) является медианой и высотой, следовательно, (triangle AXB) – равнобедренный, следовательно, (AX=BX) .

Теорема

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство

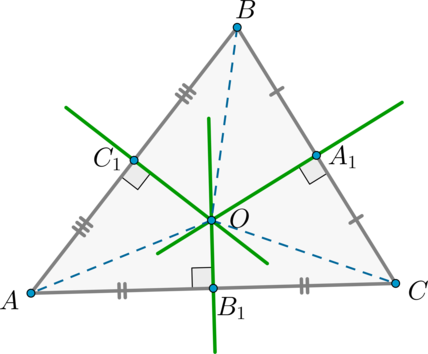
Рассмотрим (triangle ABC) . Проведем серединные перпендикуляры к сторонам (AB) и (AC) . Они пересекутся в точке (O) .

По предыдущей теореме для серединного перпендикуляра (C_1O) выполнено: (AO=BO) , а для (B_1O) — (AO=CO) . Следовательно, (BO=CO) . Значит, (triangle BOC) – равнобедренный, следовательно, высота (OA_1) , проведенная к основанию (BC) , будет также и медианой. Значит, (OA_1) – серединный перпендикуляр к отрезку (BC) .

Таким образом, все три серединных перпендикуляра пересеклись в одной точке (O) .

Следствие

Если точка равноудалена от концов отрезка, то она лежит на его серединном перпендикуляре.

Теорема

Около любого треугольника можно описать единственную окружность, причём центр описанной окружности есть точка пересечения серединных перпендикуляров к сторонам треугольника.

Доказательство

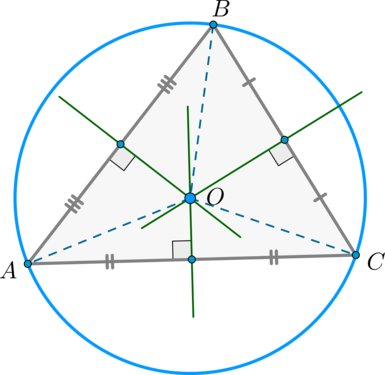
Из доказанной выше теоремы следует, что (AO=BO=CO) . Значит, все вершины треугольника равноудалены от точки (O) , следовательно, они лежат на одной окружности.

Такая окружность единственна. Допустим, что около (triangle ABC) можно описать еще одну окружность. Тогда ее центр должен совпасть с точкой (O) (т.к. это единственная точка, равноудаленная от вершин треугольника), а радиус должен быть равен расстоянию от центра до какой-то из вершин, т.е. (OA) . Т.к. у этих окружностей совпадают и центр, и радиус, то и эти окружности совпадают.

Теорема о площади вписанного треугольника

Если (a, b, c) – стороны треугольника, а (R) – радиус описанной около него окружности, то площадь треугольника [S_=dfrac]

Доказательство*
С доказательством данной теоремы рекомендуется ознакомиться после изучения темы “Теорема синусов”.

Обозначим угол между сторонами (a) и (c) за (alpha) . Тогда (S_=frac12 accdot sin alpha) .

По теореме синусов (dfrac b=2R) , откуда (sin alpha=dfrac b) . Следовательно, (S_=dfrac) .

Теорема

Около четырёхугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны (180^circ) .

Доказательство

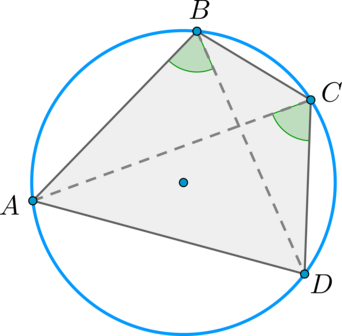
Если около четырёхугольника (ABCD) можно описать окружность, то (buildrelsmileover + buildrelsmileover = 360^circ) , откуда (angle ABC + angle ADC = fracbuildrelsmileover + fracbuildrelsmileover = frac(buildrelsmileover + buildrelsmileover) = 180^circ) . Для углов (BCD) и (BAD) аналогично.

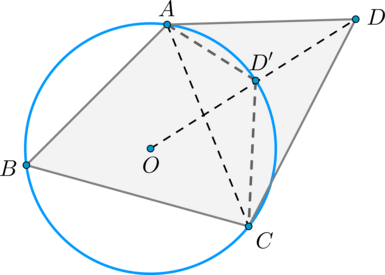
Опишем окружность около треугольника (ABC) . Пусть центр этой окружности – точка (O) . На прямой, проходящей через точки (O) и (D) отметим точку (D’) пересечения этой прямой и окружности. Предположим, что точки (D) и (D’) не совпали, тогда рассмотрим четырёхугольник (CD’AD) .

Углы (CD’A) и (CDA) дополняют угол (ABC) до (180^circ) ( (angle CDA) дополняет по условию, а (angle CD’A) по доказанному выше), следовательно, они равны, но тогда сумма углов четырёхугольника (AD’CD) больше (360^circ) , чего быть не может (сумма углов это четырёхугольника есть сумма углов двух треугольников), следовательно, точки (D) и (D’) совпадают.

Замечание. На рисунке точка (D) лежит вне круга, ограниченного окружностью, описанной около (triangle ABC) , однако, в случае, когда (D) лежит внутри, доказательство также остаётся верным.

Теорема

Около выпуклого четырехугольника (ABCD) можно описать окружность тогда и только тогда, когда (angle ABD=angle ACD) .

Доказательство

Необходимость. Если около (ABCD) описана окружность, то углы (angle ABD) и (angle ACD) – вписанные и опираются на одну дугу (buildrelsmileover) , следовательно, они равны.

Достаточность. Пусть (angle ABD=angle ACD=alpha) . Докажем, что около (ABCD) можно описать окружность.

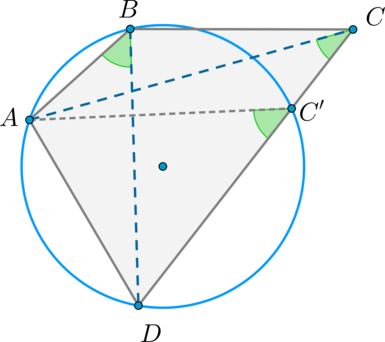
Опишем окружность около (triangle ABD) . Пусть прямая (CD) пересекла эту окружность в точке (C’) . Тогда (angle ABD=angle AC’D Rightarrow angle AC’D=angle ACD) .

Следовательно, (angle CAD=angle C’AD=180^circ-angle ADC-angle AC’D) , то есть (triangle AC’D=triangle ACD) по общей стороне (AD) и двум прилежащим углам ( (angle C’AD=angle CAD) , (angle ADC’=angle ADC) – общий). Значит, (DC’=DC) , то есть точки (C’) и (C) совпадают.

Теоремы

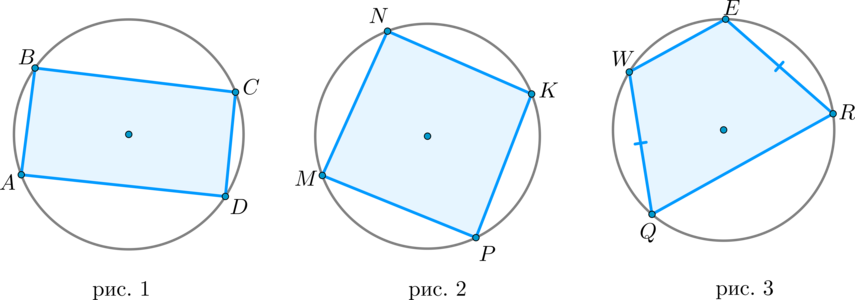
1. Если около параллелограмма описана окружность, то он – прямоугольник (рис. 1).

2. Если около ромба описана окружность, то он – квадрат (рис. 2).

3. Если около трапеции описана окружность, то она равнобедренная (рис. 3).

Верны и обратные утверждения: около прямоугольника, ромба и равнобедренной трапеции можно описать окружность, и притом только одну.

Доказательство

1) Пусть около параллелограмма (ABCD) описана окружность. Тогда суммы его противоположных углов равны (180^circ: quad angle A+angle C=180^circ) . Но в параллелограмме противоположные углы равны, т.к. (angle A=angle C) . Следовательно, (angle A=angle C=90^circ) . Значит, по определению (ABCD) – прямоугольник.

Обратное утверждение очевидно.

2) Пусть около ромба (MNKP) описана окружность. Аналогично предыдущему пункту (т.к. ромб является параллелограммом) доказывается, что (MNKP) – прямоугольник. Но все стороны этого прямоугольника равны (т.к. он ромб), значит (MNKP) – квадрат.

Обратное утверждение очевидно.

3) Пусть около трапеции (QWER) описана окружность. Тогда (angle Q+angle E=180^circ) . Но из определения трапеции следует, что (angle Q+angle W=180^circ) . Следовательно, (angle W=angle E) . Т.к. углы при основании (WE) трапеции равны, то она равнобедренная.