Презентация была опубликована 8 лет назад пользователемТарас Зотов
- Похожие презентации
- Презентация на тему: » Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.» — Транскрипт:
- Презентация к онлайн-уроку «Правильный многоугольник. Окружность вписанная и описанная около правильного многоугольника»
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Вписанные и описанные многоугольники.
- 🎦 Видео
Похожие презентации
Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Презентация на тему: » Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.» — Транскрипт:
3 Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.
4 Центр вписанной окружности – точка пересечения биссектрис всех внутренних углов многоугольника. Радиус вписанной окружности вычисляется по формуле: r= S/p, где S – площадь, а p – полупериметр многоугольника.
5 Не во всякий многоугольник можно вписать окружность.
6 В любом описанном четырёхугольнике суммы противоположных сторон равны. А В АВ + СД = ВС + АД С Д Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность.
7 В любой треугольник можно вписать окружность. Центр окружности — точка пересечения биссектрис треугольника. А О В С
8 Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник — вписанным в эту окружность.
9 Центр описанной окружности лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определённого любыми тремя вершинами данного многоугольника.
10 Около любого треугольника можно описать окружность. Центр окружности — точка пересечения серединных перпендикуляров к сторонам треугольника. R= = = R =
11 Около четырёхугольника не всегда можно описать окружность.
12 Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180°. A + C = B + D=180°
13 В прямоугольном треугольнике центр описанной окружности совпадает с серединой гипотенузы.(гипотенуза является диаметром) Радиус вписанной окружности находится по формуле:, где а и b – катеты, с – гипотенуза. R = d/2 О r =
14 Только около равнобокой трапеции можно описать окружность. В равнобедренную трапецию можно вписать окружность, если боковая сторона равна средней линии.
15 Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника. Решение. Из формулы S=pr, где p — полупериметр, находим, что периметр описанного многоугольника равен отношению удвоенной площади к радиусу вписанной окружности: Ответ: 24.
16 Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6. Решение. Радиус окружности, вписанной в равносторонний треугольник, равен одной трети высоты. Поэтому он равен 2. Ответ: 2.
17 Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника. Решение. значит, Ответ: 18.
18 Сторона правильного треугольника равна 3. Найдите радиус окружности, вписанной в этот треугольник. Решение. Радиус вписанной в треугольник окружности равен отношению площади к полупериметру: Ответ: 0,5..
19 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника. Отрезки касательных, проведенных к окружности из точек K,H,O,F,N,M соответственно равны друг другу. Поэтому Следовательно, Ответ: 24. Решение.
20 Катеты равнобедренного прямоугольного треугольника равны Найдите радиус окружности, вписанной в этот треугольник. Решение. Ответ: 1.
21 Решение. Треугольник правильный, значит, все углы равны по 60°. Сторона правильного треугольника равна3. Найдите радиус окружности, описанной около этого треугольника. Ответ: 1.
22 Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника. Решение. Вписанный угол, опирающийся на диаметр окружности, является прямым, значит, гипотенуза является диаметром и R = 12/2=6. Ответ: 6.
23 Сторона треугольника равна 1. Противолежащий ей угол равен 30°. Найдите радиус окружности, описанной около этого треугольника. Решение. По теореме синусов имеем: Ответ: 1.
24 Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника. Решение. Для нахождения площади треугольника, воспользуемся формулой Герона S = Ответ: 25
25 Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции. Решение. В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда АВ + СД = ВС + АД Ответ: 4.
26 Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:2:3. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 32. Решение. В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда АВ+СД = АД+ВС. Пусть меньшая сторона равна х, тогда х +3х=Р/2; 4х=16; х=4. Тогда большая сторона равна Р/2 – 4=16-4=12 Ответ: 12
27 Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции. Решение. Трапеция – равнобедренная, т. к. вокруг неё описана окружность. Ответ: 6.
28 Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции. Решение. Окружность, описанная вокруг трапеции, описана и вокруг треугольника ADC. Это треугольник равнобедренный, угол при вершине равен 120°, углы при основании равны 30°. Найдем его боковую сторону: AD=DC=AB-2AH=AB-2ADcos 60°=12-AD, откуда AD=6 Ответ: 6.
29 Углы А, В и С четырехугольника АВСД относятся как1:2:3. Найдите угол Д, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах. Решение. Пусть угол А равен х°. Учитывая, что сумма противоположных углов во вписанном четырёхугольнике равна 180°, получим: х+3х=180; 4х=180; х=45. Угол В равен 2х=2·45=90. Тогда угол Д равен =90. Ответ: 90. Ответ: 90º
30 Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах. Решение. Так как во вписанном четырёхугольнике сумма противоположных углов равна 180°, то больший угол равен 180° — 58°= 122° Ответ: 122.
31 Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности. Решение. Рассмотрим треугольник АОВ. Он равносторонний, т.к. АО=ОВ=R и угол АОВ равен 60°, тогда D=2R=2АО= 2АВ=2·12=24 Ответ: 24.
32 Около окружности, радиус которой равен 3/2, описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника. Решение. Угол правильного шестиугольника равен 120°, тогда угол ОАH в прямоугольном треугольнике OAH равен 60°. Следовательно, Ответ: 1.
33 C4. В треугольнике АВС известны стороны: АВ=6, ВС=8, АС=9. Окружность, проходящая через точки А и С, пересекает прямые ВА и ВС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL. Решение. Обе точки K и L не могут лежать вне треугольника, поскольку в этом случае отрезок KL не может касаться вписанной окружности. Значит, по крайней мере одна из этих точек лежит на стороне треугольника. 1)Пусть обе точки K и L лежат на сторонах треугольника. Четырехугольник AKLC вписанный, следовательно, Значит, треугольник ABC подобен треугольнику LBK, так как угол ABC общий. Пусть коэффициент подобия равен k, тогда BL=kAB, BK=kBC, KL=kAC. Суммы противоположных сторон описанного четырехугольника AKLC равны: Подставляя известные значения сторон, находим k = = KL=kAC=45/23
34 2)Пусть точка K лежит на продолжении стороны AB. Углы AKL и ACL равны, поскольку опираются на одну дугу. Значит, треугольник ABC подобен треугольнику LBK, так как угол ABC общий. Более того, они описаны около одной и той же окружности. Следовательно, коэффициент подобия равен 1, то есть, треугольники LBK и ABC равны, поэтому KL=AC= 9. Заметим, что BK=BC>AB и точка K действительно лежит на продолжении стороны AB. Если точка L лежит на продолжении стороны BC, то BL>BC, но, аналогично предыдущему случаю, получаем BL=AB AB и точка K действительно лежит на продолжении стороны AB. Если точка L лежит на продолжении стороны BC, то BL>BC, но, аналогично предыдущему случаю, получаем BL=AB»>
35 C 4.Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключённый внутри треугольника, равен 24, а отношение катетов треугольника равно 5/12. Решение. Обозначим треугольник АВС, отношение катетов равен 5/12, АС=5х-катет, ВС=12х-катет, АВ=13х гипотенуза. Заметим, что окружность, о которой говорится в условии, окружность, вписанная в треугольник ABC. Пусть О её центр, а D и Е точки касания с катетами АС и ВС соответственно. Тогда, так как ODCE квадрат, радиус этой окружности. OD=EC= = = 2x. Пусть прямая MN перпендикулярна АВ, касается окружности, пересекает АВ в точке М, а АС в точке N. Прямоугольный т реугольник ANM подобен треугольнику ABC. В нём MN=24, AM=26, AN=10. У описанного четырёхугольника суммы противоположных сторон равны: ВС+MN=BM+CN; 12х+24=(13х-26)+(5х-10), откуда находим: х=10. r=2x=20
36 Пусть прямая MN перпендикулярна АВ, касается окружности, пересекает АВ в точке М, а ВС в точке N. Прямоугольный треугольник NBM подобен треугольнику ABC. В нём MN=24, BM=57,6, BN=62,4. У описанного четырёхугольника суммы противоположных сторон равны: MN+AC=CN+AM; 24+5x=(12x-62,4)+(13x-57,6), откуда находим: х=7,2. r=2x=14,4 Ответ: 20 или 14,4.
Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Презентация к онлайн-уроку «Правильный многоугольник. Окружность вписанная и описанная около правильного многоугольника»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Правильный многоугольник. Окружность вписанная и описанная около правильного многоугольника.
Правильный многоугольник.
Правильным многоугольником называется выпуклый многоугольник,
у которого все углы равны и все стороны равны
Описанная окружность.
Окружность называется
ОПИСАННОЙ около многоугольника, если
все вершины многоугольника лежат на этой окружности
Около любого правильного многоугольника можно описать окружность, и притом только одну
A1
A2
A3
A4
A5
An
O
1
2
3
4
(по двум сторонам и углу между ними)
?
Вписанная окружность.
ОКРУЖНОСТЬ называется
ВПИСАННОЙ В МНОГОУГОЛЬНИК, если
все стороны многоугольника касаются этой окружности
Вписанная окружность.
ОКРУЖНОСТЬ называется
ВПИСАННОЙ В МНОГОУГОЛЬНИК, если
все стороны многоугольника касаются этой окружности
O
A1
A2
A3
A4
A5
An
H1
H2
H3
H4
Hn
В любой правильный многоугольник можно
вписать окружность, и притом только одну .
СЛ.1. Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах
СЛ.2. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник
т.О – центр правильного многоугольника
П.109 — 111, №1081, 1082, 1083, 1084
Домашнее задание:
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 989 человек из 79 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 681 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 313 человек из 70 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Дистанционные курсы для педагогов
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 525 653 материала в базе
Материал подходит для УМК
«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
§ 1. Правильные многоугольники
Другие материалы
- 31.01.2022
- 11
- 0
- 31.01.2022
- 45
- 0
- 31.01.2022
- 35
- 0
- 31.01.2022
- 39
- 0
- 31.01.2022
- 35
- 0
- 31.01.2022
- 69
- 1
- 31.01.2022
- 8
- 0
- 31.01.2022
- 40
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 31.01.2022 126
- PPTX 698.4 кбайт
- 6 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Лаптева Юлия Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 3 года и 3 месяца
- Подписчики: 23
- Всего просмотров: 28770
- Всего материалов: 75
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Рособрнадзоре видят предпосылки к снижению качества знаний у школьников на фоне пандемии
Время чтения: 1 минута
В Свердловской области школьников со 2 по 8 класс и студентов переводят на удаленку
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
В Тульской области ввели школьные каникулы со 2 по 11 февраля
Время чтения: 1 минута
В России планируют создадут сеть центров для подростков «группы риска»
Время чтения: 1 минута
В Томске студентов вузов перевели на дистанционное обучение до конца февраля
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Вписанные и описанные многоугольники.
Определение. Если все стороны многоугольника касаются окружности, то многоугольник называется описанным около окружности, а окружность – вписанной в многоугольник.
Определение. Если все вершины многоугольника лежат на окружности, то многоугольник называется вписанным в эту окружность, а окружность – описанной около треугольника.
| Вписанная окружность | Описанная окружность |
Треугольник 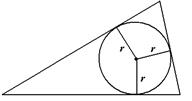 Центр – точка пересечения биссектрис. Центр – точка пересечения биссектрис. 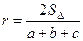 . . | 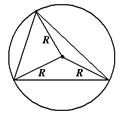 Центр – точка пересечения серединных перпендикуляров. Центр – точка пересечения серединных перпендикуляров. 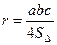 . . |
| Параллелограмм НЕТ | НЕТ |
Ромб 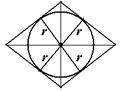 Центр – точка пересечения диагоналей. Радиус окружности равен половине высоты ромба, т.е. Центр – точка пересечения диагоналей. Радиус окружности равен половине высоты ромба, т.е. 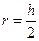 . . | НЕТ |
| Прямоугольник НЕТ | 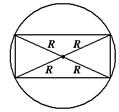 Центр – точка пересечения диагоналей. Радиус окружности равен половине длины диагонали прямоугольника, т.е. Центр – точка пересечения диагоналей. Радиус окружности равен половине длины диагонали прямоугольника, т.е. 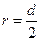 . . |
Квадрат 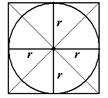 Центр – точка пересечения диагоналей. Радиус окружности равен половине длины стороны квадрата, т.е. Центр – точка пересечения диагоналей. Радиус окружности равен половине длины стороны квадрата, т.е. 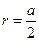 . . | 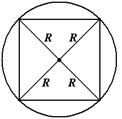 Центр – точка пересечения диагоналей. Радиус окружности равен половине длины диагонали квадрата, т.е. Центр – точка пересечения диагоналей. Радиус окружности равен половине длины диагонали квадрата, т.е. 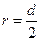 . . |
Трапеция 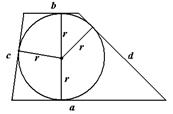 Центр – точка пересечения биссектрис. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е. Центр – точка пересечения биссектрис. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е. 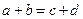 . Радиус окружности равен половине длины высоты трапеции, т.е. . Радиус окружности равен половине длины высоты трапеции, т.е. 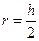 . . | 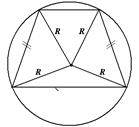 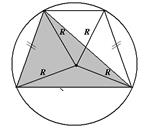 Центр – точка пересечения серединных перпендикуляров. Около трапеции можно описать окружность тогда и только тогда, когда трапеция равнобедренная. Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины трапеции (любые три из четырех у трапеции). Центр – точка пересечения серединных перпендикуляров. Около трапеции можно описать окружность тогда и только тогда, когда трапеция равнобедренная. Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины трапеции (любые три из четырех у трапеции). |
Произвольный выпуклый четырехугольник 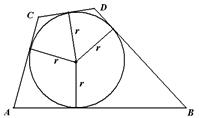 Центр – точка пересечения биссектрис. В произвольный выпуклый четырехуголь-ник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е. Центр – точка пересечения биссектрис. В произвольный выпуклый четырехуголь-ник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е. 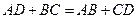 . Общего способа и формулы для вычисления длины радиуса нет. . . Общего способа и формулы для вычисления длины радиуса нет. . | 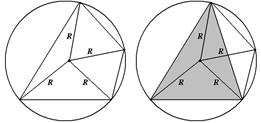 Центр – точка пересечения серединных перпендикуляров. Около произвольного выпуклого четырехугольника можно описать окружность тогда и только тогда, когда суммы противоположных углов равны Центр – точка пересечения серединных перпендикуляров. Около произвольного выпуклого четырехугольника можно описать окружность тогда и только тогда, когда суммы противоположных углов равны 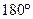 . Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины данного четырехугольника (любые три из его четырех). Теорема 39. (Птолемея). В четырехуголь-нике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон. . Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины данного четырехугольника (любые три из его четырех). Теорема 39. (Птолемея). В четырехуголь-нике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон. 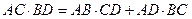 |
Определение. Выпуклый многоугольник называется правильным, если у него все углы равны и стороны равны.
Теорема 38. Около любого правильного многоугольника можно описать окружность и притом только одну.
Теорема 39. В любой правильный многоугольник можно вписать окружность и притом только одну.
🎦 Видео
8 класс, 2 урок, Выпуклый многоугольникСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Окружность, вписанная в правильный многоугольник | Геометрия 7-9 класс #106 | ИнфоурокСкачать

МногоугольникСкачать

9 класс, 21 урок, Правильный многоугольникСкачать

Геометрия 9 класс : Правильные многоугольникиСкачать

Вписанная окружность | Геометрия 7-9 класс #74 | ИнфоурокСкачать

ГЕОМЕТРИЯ 8 класс : Вписанная окружностьСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

✓ Экстремальная задача про правильный вписанный многоугольник | Ботай со мной #078 | Борис ТрушинСкачать

Окружность, вписанная в правильный многоугольник. Видеоурок по геометрии 9 классСкачать

Вписанные и описанные многоугольникиСкачать








