Если вектор равен заданному вектору то это

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

рис. 1

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Примеры задач на равенство векторов

Примеры плоских задач на равенство векторов

a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y => 8 = 2 n => n = 8/2 = 4

Ответ: при n = 4 вектора a и b равны.

Примеры пространственных задач на равенство векторов

a = c — так как их координаты равны,
a ≠ b — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y = 2
a_z = b_z => 4 = 2 n => n = 4/2 = 2

Ответ: при n = 2 вектора a и b равны.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Вектор. Виды векторов.

Вектор — в самом элементарном случае это математический объект, который характеризуется

величиной и направлением.

В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая

из его граничных точек является началом, а какая — концом.

У вектора есть длина и определенное направление. Графически вектора изображаются как

направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.

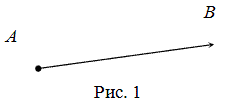
Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Как видно на рисунке, начало отрезка – это точка А, концом отрезка является

точка В, а непосредственно вектор обозначен через . У направления

вектора существенное значение, если переместить стрелку на другую

сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора

удобно сравнивать с движением физического тела: подумайте, ехать на

рыбалку и с рыбалки – разница огромная.

Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть

разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.

Виды векторов.

Единичным называется вектор, длина которого равна 1.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.

У такого вектора конец и начало совпадают.

Нулевой вектор обычно обозначается как . Длина нулевого вектора, или его модуль равен нулю.

Коллинеарные вектора – вектора, которые параллельны одной прямой

или которые лежат на одной прямой.

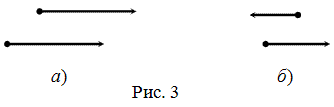
Сонаправленные вектора. Два коллинеарных вектора a и b называются

сонаправленными векторами только тогда, когда их направления

соответствуют друг другу: a↑↑b

Противоположно направленные вектора – два коллинеарных вектора

a и b называются противоположно направленными векторами, только

когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной

плоскости или те, которые лежат на общей плоскости.

В любое мгновение существует плоскость одновременно параллельную

двум любым векторам, поэтому два произвольных вектора являются

Равные вектора. Вектора a и b будут равными, если они будут лежать на

одной либо параллельных прямых и их направления и длины одинаковые.

То есть, такой вектор можно перенести параллельно ему в каждое место

Таким образом, два вектора равны, если они коллинеарные, сонаправленые

и имеют одинаковые длины:

Для координатного представления векторов огромное значение

оказывает понятие проекции вектора на ось (направленную

прямую).

Проекция вектора — это длина отрезка, который образуется

проекциями точек начала и конца вектора на заданную прямую,

при этом проекции добавляется знак “+”, но когда направление

проекции соответственно направлению оси, иначе — знак “–”.

Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция

вектора на ось, которая перпендикулярна ему = 0.

Когда работают с векторами, зачастую вводят так называемую

декартову систему координат и уже в этой системе находят

координаты вектора по базисным векторам.

Разложение по базису геометрически можно показать проекцией

вектора на координатные оси. Когда известны координаты начала и

конца вектора, то координаты данного вектора получают вычитая

из координат конца вектора координат начала вектора.

За базис зачастую выбираются координатные орты, которые обозначаются как , соответственно

осям x, y, z. Исходя из этого, вектор можно записать в таком виде:

Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование

из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,

кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только

те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Векторы: основные определения и понятия

Скалярная величина — величина, которая может быть охарактеризована числом. Например, длина, площадь, масса, температура и т.д.

Вектором называется направленный отрезок $overline$; точка $A$ — начало, точка $B$ — конец вектора (рис. 1).

Вектор обозначается либо двумя большими буквами — своим началом и концом: $overline$ либо одной малой буквой: $overline$.

Если начало и конец вектора совпадают, то такой вектор называется нулевым. Чаще всего нулевой вектор обозначается как $overline$.

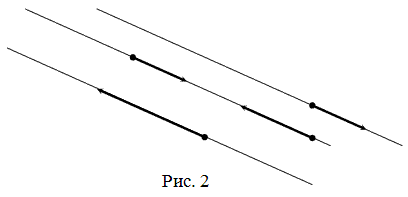
Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2).

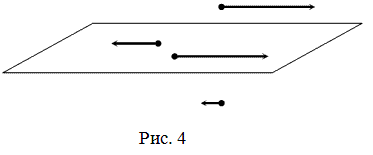
Векторы называются компланарными, если они параллельны одной плоскости или лежат в одной плоскости (рис. 4).

Два вектора всегда компланарны.

Длиной (модулем) вектора $overline$ называется расстояние между его началом и концом: $|overline|$

Подробная теория про длину вектора по ссылке.

Длина нулевого вектора равна нулю.

Вектор, длина которого равна единице, называется единичным вектором или ортом.

Векторы называются равными, если они лежат на одной или параллельных прямых; их направления совпадают и длины равны.

Иначе говоря, два вектора равны, если они коллинеарны, сонаправлены и имеют равные длины:

В произвольной точке $M$ пространства можно построить единственный вектор $overline$, равный заданному вектору $overline$.

📹 Видео

Координаты вектора. 9 класс.Скачать

Координаты вектора в пространстве. 11 класс.Скачать

Угол между векторами | МатематикаСкачать

Скалярное произведение векторов. 9 класс.Скачать

Равенство векторов. 9 класс.Скачать

#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Найдите разложение вектора по векторам (базису)Скачать

Вектор. Определение. Коллинеарные векторы. Равные векторы.Скачать

Разложение вектора по базису. 9 класс.Скачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Как разложить вектор по базису - bezbotvyСкачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Геометрия 10 класс (Урок№17 - Вектор в пространстве.)Скачать