Если r и m радиус вектор и масса (5 видео) | Курс школьной геометрии

Определение центра масс

При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.

Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.

Содержание

Радиус-вектор и координаты центра масс
Скорость центра масс
Примеры задач на определение центра масс
Если r и m радиус вектор и масса
Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.
Траектория движения материальной точки через радиус-вектор
Вектор скорости материальной точки
Пример нахождения вектора скорости
Как найти вектор ускорения материальной точки
Модуль вектора скорости точки
Модуль вектора ускорения
Еще примеры решений задачи нахождения вектора скорости и ускорения
🎬 Видео

Видео:Радиус-векторыСкачать

Радиус-вектор и координаты центра масс

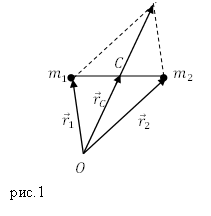
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: $<overline>_1 и <overline>_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором $<overline>_C$ (рис.1).

Из рис.1 видно, что:

Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен $<overline>_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:

Радиус -вектор $<overline>_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц $<overline>_1$ и $<overline>_2$. Это становится очевидным, если формулу (2) представить в виде:

Выражение (3) показывает, что радиус-вектор каждой частицы входит в $<overline>_C$ с весом, который пропорционален его массе.

Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.

Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:

Выражение (4) считают определением центра масс системы.

При этом абсцисса центра масс равна:

Ордината ($y_c$) центра масс и его аппликата ($z_c$):

Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Скорость центра масс

Выражение для скорости центра масс ($<overline>_c=frac<d<overline>_c>

$) запишем как:

где $overline

$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.

Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.

Видео:Радиус векторСкачать

Примеры задач на определение центра масс

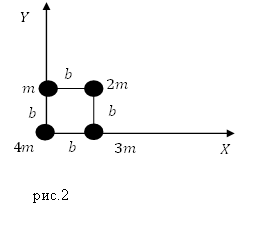
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?

Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:

Вычислим массу рассматриваемой системы точек:

Тогда абсцисса центра масс $x_ $равна:

Ответ. $x_c=0,5 b$; $y_с=0,3 b$

Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.

Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.

В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:

Видео:ЕГЭ по Физике 2022. Кинематика. Радиус-векторСкачать

Если r и m радиус вектор и масса

Глава 14. Теоремы о движении центра масс и об изменении количества движения и кинетического момента.

14.1. Теорема о движении центра масс.

14.1.1. Положение центра масс С механической системы массой m = 50 кг определяется радиусом-вектором r_с = 3i + 4j + 5k. Опрeделить статический момент масс этой системы относительно плоскости Оху. (Ответ 250)

14.1.2. Определить координату хс центра масс кривошипно-ползунного механизма при углах φ = 90 о и α = 30°, если масса кривошипа 1 равна 4 кг, а масса шатуна 2 равна 8 кг. Шатун 2 длиной 0,8 м считать однородным стержнем. Массой ползуна 3 пренебречь. (Ответ 0,231)

14.1.3. Тело массой m = 2 кг движется по горизонтальным направляющим согласно закону s = 2t 2 + 1. Определить модуль главного вектора внешних сил, действующих на тело. (Ответ 8)

14.1.4. Тело 1 массой m = 50 кг поднимается по наклонной плоскости с помощью троса, наматываемого на барабан 2 радиуса R = 0,4 м. Определить модуль главного вектора внешних сил, действующих на тело 1, если угловое ускорение барабана ϵ = 5 рад/с 2 . (Ответ 100)

14.1.5. Механическая система движется так, что проекции ускорения ее центра масс С на оси координат равны а_Сх = 1 м/с 2 , а_Су = 2 м/с 2 , a_Cz = 4 м/с 2 . Определить модуль главного вектора внешних сил, действующих на систему, если масса системы m = 40 кг. (Ответ 183)

14.1.6. Движение центра масс механической системы определяется радиусом-вектором r_с = 2 cos πti + 2 sin πtj. Определить проекцию на ось Оу главного вектора внешних сил в момент времени t = 0,5 с, если масса системы m = 10 кг. (Ответ -197)

14.1.7. Диск массой m = 20 м вращается равномерно вокруг неподвижной оси с угловой скоростью ω = 10 рад/с. Определить модуль главного вектора внешних сил, приложенных к диску, если его центр тяжести удален от оси вращения на расстояние ОС = 0,5 см. (Ответ 10)

14.1.8. Центр масс колеса С движется по окружности радиуса R = 1,3 м согласно закону s = 4t. Определить модуль главного вектора внешних сил, приложенных к колесу, если его масса m = 15 кг. (Ответ 185)

14.1.9. Кривошип 1 шарнирного параллелограмма вращается равномерно с угловой скоростью ω₁ = 5 рад/с. Определить модуль главного вектора внешних сил, действующих на звено 2, если его масса m = 8 кг, длина ОА = 0,4 м. (Ответ 80)

14.1.10. Однородный равносторонний треугольник ОАВ массой m = 5 кг вращается равномерно вокруг неподвижной оси. Определить его угловую скорость ω, если главный вектор внешних сил, действующих на него, равен 300Н, а длина l = 0,4 м. (Ответ 16,1)

14.1.11. Шкив 2 радиуса R = 0,2 м, вращаясь с угловым ускорением ϵ₂ = 10 рад/с 2 , поднимает однородный цилиндр 1, масса которою m = 50 кг. Определить модуль главного вектора внешних сил, действующих на цилиндр. (Ответ 50)

14.1.12. Однородный диск радиуса R = 0,5 м, масса которого m = 20 кг, вращается с постоянным угловым ускорением ϵ = 10 рад/с 2 . Определить модуль главного вектора внешних сил, действующих на диск. (Ответ 0)

14.1.13. Однородный стержень ОА массой m = 10 кг вращается равномерно с угловой скоростью ω = 10 рад/с. Определить модуль главного вектора внешних сил, действующих на стержень, если его длина ОА = 1 м. (Ответ 500)

14.1.14. Ползун А движется под действием силы F с постоянной скоростью v_A. Определить реакцию направляющей на ползун А в тот момент времени, когда ускорение ползуна В равно а_в = 4 м/с 2 , если масса однородного стержня АВ равна 5 кг. Массой ползунов пренебречь.
(Ответ 10)

14.1.15. Кривошип 1 длиной ОА = 0,25 м, вращаясь равномерно с угловой скоростью ω = 10 рад/с, приводит в движение кулису 2, масса которой m = 5 кг. Определить модуль главного вектора внешних сил, действующих на кулису в момент времени, когда угол φ = 60°.
(Ответ 62,5)

14.1.16. Определить модуль главного вектора внешних сил, действующих на шатун АВ кривошипно-ползунного механизма в момент времени, когда угол φ = 180°, а точки А и В имеют ускорения а_А = 10 м/с 2 , а_в = 14 м/с 2 . Шaтун массой m = 5 кг считать однородным стержнем. (Ответ 60)

14.1.17. Определить проекцию ускорения центра масс С механической системы на ось О_у в момент времени, когда координата у_С = 0.8 м, если масса системы m = 10 кг, а главный вектор приложенных внешних сил R e = 3i + 6tj. В начальный момент времени центр масс системы находился в точке О в покое. (Ответ 1,2)

14.1.18. Тело 1 массой 4 кг может двигаться по горизонтальной направляющей. На какое расстояние переместится тело 1, когда однородный стержень 2 массой 2 кг и длиной l = 0,6 м. опускаясь под действием силы тяжести, займет вертикальное положение. В начальный момент система находилась в покое. (Ответ 0,1)

14.1.19. Тело 1 массой m₁ = 0,7 кг может двигаться по горизонтальной направляющей. Определить модуль ускорения тела 1 в момент времени t = 0,25 с, если относительно него под действием внутренних сил системы движется тело 2 массой m₂ = 0,1 кг согласно уравнению s = sin 4t. (Ответ 0,841)

14.1.20. На тело 1 действует постоянная сила F = 10Н. Определить ускорение этого тела в момент времени t = 0,5 с, если относительно него под действием внутренних сил системы движется тело 2 согласно уравнению x = cos πt. Массы тел: m₁ = 4 кг, m₂ = 1 кг. Тела движутся поступательно. (Ответ 2)

14.1.21. Определить ускорение тела 1, скользящего но гладкой наклонной плоскости, если в горизонтальных направляющих относительно него под действием внутренних сил системы движется тело 2 согласно уравнению x = t 2 . Массы тел: m₁ = m₂ = 1 кг. Тела движутся поступательно. (Ответ 4,04)

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Видео:Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Видео:10 Класс - Физика - Перемещение. Радиус-вектор.Скачать

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Видео:3.3. Центр масс и закон его движения | Динамика | Александр Чирцов | ЛекториумСкачать

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Видео:Вращательное движение. 10 класс.Скачать

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.