Если прямая параллельна линии пересечения двух плоскостей то она параллельна обоим плоскостям

Геометрия | 5 — 9 классы

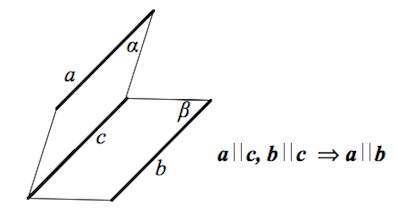
Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения.

Пусть это не так.

Очевидно, что прямая не может пересекать прямую пересечения плоскостей, так как в этом случае она не будет параллельна плоскостям.

Пусть они скрещиваются.

Через прямую, скрещивающуюся с данной можно провести только одну плоскость, параллельную данной прямой, значит, 2 плоскости совпадают.

Видео:Параллельность прямой к плоскостиСкачать

Доказать, что если через каждую из двух параллельных прямых провести плоскости и они пересекаются , то линия пересечения параллельна каждой из них?

Доказать, что если через каждую из двух параллельных прямых провести плоскости и они пересекаются , то линия пересечения параллельна каждой из них.

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Докажите что все прямые пересекающие каждую из двух параллельных прямых лежат в одной плоскости?

Докажите что все прямые пересекающие каждую из двух параллельных прямых лежат в одной плоскости.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Плоскости Альфа и Бета пересекаются по прямой С?

Плоскости Альфа и Бета пересекаются по прямой С.

Плоскость Омега, параллельная прямой С, пересекает плоскости Альфа и Бета по прямым а и b соответственно.

Докажите, что a параллельна Бета и b параллельна Альфа.

Видео:02. Построение прямой пересечения двух плоскостейСкачать

Плоскости a и в параллельны, причем плоскость а пересекает некоторую прямую а?

Плоскости a и в параллельны, причем плоскость а пересекает некоторую прямую а.

Докажите , что и плоскость в пересекает прямую а.

Видео:№25. Докажите, что если данная прямая параллельна прямой, по которой пересекаютсяСкачать

Докажите, что если плоскость проходит через прямую, параллельную другой прямой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой?

Докажите, что если плоскость проходит через прямую, параллельную другой прямой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Докажите, что если прямая пар — на каждой из двух пересекающихся плоскостей, то она она параллельна линии их пересечания?

Докажите, что если прямая пар — на каждой из двух пересекающихся плоскостей, то она она параллельна линии их пересечания.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Помогите кто нибудь пожалуйста?

Помогите кто нибудь пожалуйста!

Докажите, что Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Докажите свойство линии пересечения двух параллельных плоскостей третьей плоскостью?

Докажите свойство линии пересечения двух параллельных плоскостей третьей плоскостью.

Видео:6. Параллельность прямой и плоскостиСкачать

Верно ли утверждение : если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость?

Верно ли утверждение : если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость.

Видео:Взаимное пересечение двух плоскостейСкачать

Верно ли утверждение : если одна из двух прямых параллельна плоскости, а вторая пересекает эту плоскость, то прямые параллельны( и почему)?

Верно ли утверждение : если одна из двух прямых параллельна плоскости, а вторая пересекает эту плоскость, то прямые параллельны( и почему).

Вы зашли на страницу вопроса Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Противоположные стороны параллелограмма равны. Периметр — сумма четырех сторон, значит сумма двух разных сторон равна 32 : 2 = 16см. Из соотношения можно написать, что одна сторона равна Х, а вторая 3Х. Тогда 4Х = 16см, Х = 4см, а большая сторона ..

1. Нулевой вектор коллинеарен любому вектору : Если = (или = ), то||(или||). 2. Нулевой вектор одинаково направлен с любым вектором, . 3. Любые два коллинеарных вектора можно отложить на одной прямой. Достаточно отложить векторы от одной точки. 4..

Угол N = M = 35 Угол О = 180 — (35 + 35) = 110.

15″ = 10″ + х» х» = 15″ — 10″ х = 5 S = 1 / 2 высоты * на сторону, к которой она проведена S = 1 / 2 * 5 * 10 S = 25 см2 » — квадрат ( 15″ — 15 в квадрате).

Дано : АВС , АВ = ВС = 15 см АС = 10Найти : S — ? Решение : Высота, опущенная из вершины равнобедренного треугольника на его основание является одновременно и высотой, и медианой. ВН — высотаАН = НС = 5 смТреугольник АВН — прямоугольный, катет АН =..

Только если в общем виде , если будет. Дан угол прорстро получать и посчитай.

Ииосноваа Х сотая ле врмпо флтсяаходции аходции адь трапплощадей.

DOA по двум углам (накрест лежащим) , BO : OD = OC : AO = BC : AD = 2 : 3 2AO = 3OC AO + OC = 20 2AO + 2OC = 40 5OC = 40 OC = 8 AO = 12.

OB = OA, OC = CO(общая сторона), AC = BC.

1)тр. АОС = тр. ОСВ (по двум катетам) = > АС = ВС(соотв. Элементы).

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

10 класс. Геометрия. Параллельные прямые в пространстве. Решение задач

10 класс. Геометрия. Параллельные прямые в пространстве. Решение задач

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:Построение линии пересечения двух плоскостейСкачать

Определение параллельных прямых

Определение: две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются (рис. 1).

Рис. 1. Параллельные прямые

Видео:Линия пересечения плоскостейСкачать

Лемма

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Пояснение к лемме

Даны две параллельные прямые а и b. Прямая а пересекает плоскость в точке М. Лемма утверждает, что прямая b тоже пересекает плоскость в некоторой точке, назовем ее N (рис. 2).

Рис. 2. Иллюстрация к лемме

Видео:№57. Прямая а параллельна одной из двух параллельных плоскостей. Докажите, что прямаяСкачать

Определение параллельности прямой и плоскости

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Признак параллельности прямой и плоскости

Теорема (признак параллельности прямой и плоскости)

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Пояснение к признаку.

Дана плоскость , прямая b лежит в плоскости α, прямая а параллельна прямой b, прямая а не лежит в плоскости (рис. 3). Согласно признаку параллельности прямой и плоскости, прямая а параллельна всей плоскости α. Мощь этого признака в том, что только из того, что прямая а не имеет общих точек с прямой b (небольшой частью всей плоскости), следует, что прямая а не имеет общих точек со всей плоскостью.

Рис. 3. Иллюстрация к признаку

Следующее утверждение часто используется для решения задач.

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Утверждение 1

Если плоскость проходит через данную прямую а, параллельную другой плоскости (а || ), и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой: a || b.

Дана плоскость и прямая а, которая параллельна плоскости (рис. 4). Через прямую а проходит плоскость , которая пересекает плоскость по некоторой прямой b . Согласно утверждению, линия пересечения плоскостей и – прямая b будет параллельна прямой а.

Рис. 4. Иллюстрация к утверждению

Видео:Нахождение линии пересечения плоскостей путём приглашения плоскостей посредниковСкачать

Задача 1

Треугольники ABC и ABD не лежат в одной плоскости. Докажите, что любая прямая, параллельная отрезку СD, пересекает плоскости данных треугольников.

Рис. 5. Иллюстрация к задаче

Нам дано, что точка D не лежит в плоскости АВС, а точка С не лежит в плоскости АВD. Нужно доказать, что любая прямая, назовем ее m, параллельная прямой СD, пересечет плоскости АВС и АВD.

Вспомним лемму, если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Прямая СD пересекает плоскость АВС в точке С. Значит, и параллельная ей прямая m пересечет эту плоскость в некоторой точке N (по лемме): .

Прямая СD пересекает плоскость ABD в точке D. Значит, и параллельная ей прямая m пересечет эту плоскость в некоторой точке M (по лемме):.

Видео:Лекция 5. Взаимное расположение двух прямых, прямой и плоскости, двух плоскостейСкачать

Задача 2

Точки А и В лежат в плоскости , а точка С не лежит в этой плоскости. Докажите, что прямая, проходящая через середины отрезков АС и ВС, параллельна плоскости .

Рис. 6. Иллюстрация к задаче

Пусть M – середина АС, N- середина ВС.

Точка М не лежит в плоскости , так как если бы она в ней лежала, то и прямая АМ, а значит и точка С, лежала бы в плоскости , что противоречит условию. Аналогично, точка N не лежит в плоскости

Рассмотрим треугольник АВС. MN – средняя линия в этом треугольнике. По свойству, MN параллельна АВ. Прямая MN параллельна прямой АВ, а прямая АВ лежит в плоскости . Значит, прямая АВ параллельна плоскости, что и требовалось доказать.

Видео:Параллельность прямых. 10 класс.Скачать

Задача 3

Плоскость параллельна стороне ВС треугольника АВС и проходит через середину стороны АВ. Докажите, что плоскость проходит через середину стороны АС.

Рис. 7. Иллюстрация к задаче

Нам даны две плоскости АВС и . Они не совпадают, имеют общую точку M, а значит, имеют линию пересечения MN. Докажем, что N – середина АС.

Плоскость АВС проходит через прямую ВС, которая по условию параллельна плоскости . Значит, ВС параллельна линии пересечения плоскостей MN.

Параллельные прямые MN и АС рассекают стороны угла А на пропорциональные части, то есть АМ : МВ = АN : NС = 1. Значит, N – середина стороны АС, что и требовалось доказать.

Видео:ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ 10 класс стереометрияСкачать

Итоги урока

Итак, мы повторили теорию и рассмотрели решение более сложных задач по теме: «Параллельность прямой и плоскости». На следующем уроке мы рассмотрим взаимное расположение прямых в пространстве.

Параллельность прямых и плоскостей

Параллельные прямые

Параллельные прямые – прямые, которые лежат в одной плоскости и не пересекаются.

Признак параллельности прямых

Две прямые, параллельные третьей, параллельны между собой.

Параллельные прямая и плоскость

Прямая и плоскость называются параллельными , если они не имеют общих точек.

Признак параллельности прямой и плоскости

Если прямая, не принадлежащая данной плоскости, параллельна какой-нибудь прямой этой плоскости, то она параллельна этой плоскости.

Свойство прямой, параллельной данной плоскости

Если плоскость β проходит через прямую a , параллельную плоскости α , и пересекает эту плоскость по прямой b , то b || a .

Параллельные плоскости

Параллельные плоскости – плоскости, которые не пересекаются.

Признаки параллельности плоскостей

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.

Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой.

Свойства параллельных плоскостей

Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.

Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.

Чтобы не потерять страничку, вы можете сохранить ее у себя: