Если при пересечении двух прямых третьей прямой соответственные углы равны 65 то прямые параллельны

Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

4) Любые три прямые имеют не менее одной общей точки.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.» — верно, так как если соответственные углы равны, то прямые параллельны.

2) «Любые две прямые имеют не менее одной общей точки.» — неверно, две прямые имеют не более одной общей точки.

3) «Через любую точку проходит более одной прямой.» — верно, через одну точку проходит множество пересекающихся в этой точке прямых.

4) «Любые три прямые имеют не менее одной общей точки.» — неверно, любые три прямые, которые не совпадают, если и имеют общую точку, то только одну.

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

1. Если при пересечении двух прямых третьей прямой соответственные углы равны 65 , то эти две прямые параллельны?

Геометрия | 5 — 9 классы

1. Если при пересечении двух прямых третьей прямой соответственные углы равны 65 , то эти две прямые параллельны.

2. Любые две прямые имеют не менее одной общей точки.

3. Через любую точку проходит более одной прямой.

4. Любые три прямые имеют не менее одной общей точки.

1. ) Соответственные углы в сумме дают 180 градусов.

Соответственно данные прямые не параллельны.

2. ) Две прямые могут быть параллельны и тогда у них не будет не одной общей точки.

3. ) Через любую точку проходит более одной прямой) +

) Три прямые могут быть параллельны и тогда у них не будет не одной общей точки.

Видео:Теорема 14.1 Если накрест лежащие углы равны, то прямые параллельныСкачать

Укажите номера верных утверждений?

Укажите номера верных утверждений.

1) Любые две прямые имеют не менее одной общей точки.

2) Если две прямые перпендикулярны третьей прямой, то эти две прямые

3) Если угол равен 38° , то смежный с ним равен 142° .

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Две прямые , перпендикулярные третьей прямой , имеют одну точку пересечения?

Две прямые , перпендикулярные третьей прямой , имеют одну точку пересечения?

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Какие из следующих утверждений верны : 1?

Какие из следующих утверждений верны : 1.

Если при пересечении двух прямых третьей прямой соответственные углы равны 65 градусов, то эти две прямые параллельны.

2. Любые две прямые имеют не менее одной общей точки.

3. Через любую точку проходит более одной прямой.

4. Любые три прямые имеют не менее одной общей точки.

Видео:Углы при пересечении двух прямых секущей (третьей прямой). Виды углов урок 5. Геометрия 7 класс.Скачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1) через любые три точки проходит равно одна прямая.

2) сумма смежных угла равна 90 градусов.

3)Если при пересечении двух прямых третьей прямой соответственные углы составляют в сумме 180 градусов , то эти две прямые параллельны.

4) через любые две точки проходит не более одной прямой.

Видео:Углы при пересечении двух прямых третьейСкачать

Какие ответы верны?

Какие ответы верны?

1. Если при пересечении двух прямых третьей прямой соответственные углы равны 65 , то эти две прямые параллельны.

 2. Любые две прямые имеют не менее одной общей точки.

3. Через любую точку проходит более одной прямой.

4. Любые три прямые имеют не менее одной общей точки.

Видео:Углы, образованные при пересечении двух прямых секущейСкачать

1) Сколько прямых, параллельных данной прямой проходит через точку не принадлежащую прямой?

1) Сколько прямых, параллельных данной прямой проходит через точку не принадлежащую прямой?

2) Сколько общих точек имеют две прямые?

3) Сколько общих точек имеют три прямые?

4) Сколько прямые проходит через любые три точки?

5) Сколько прямых проходит через одну точку?

Видео:№65. Найдите неразвернутые углы, образованные при пересечении двух прямых,Скачать

Укажите номера верных утверждений 1) Через любую точку проходит не менее одной прямой 2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65градусам, то эти две прямые паралл?

Укажите номера верных утверждений 1) Через любую точку проходит не менее одной прямой 2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65градусам, то эти две прямые параллельны 3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90 градусов, то эти две прямые параллельны.

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Какие из следущих утверждений верны?

Какие из следущих утверждений верны?

1)любые три прямые имеют не более одной общей точки.

2)через любую точку проходит более одной прямой.

3)если две прямые пепендикулярны третьей прямой, то эти де прямые пепендикулярны.

Видео:№201. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210Скачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

Видео:Диагностическая работа в формате ОГЭ. Задача-13Скачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос 1. Если при пересечении двух прямых третьей прямой соответственные углы равны 65 , то эти две прямые параллельны?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

1) если диагональ биссектрисса, то параллелограмм является ромбом. Значит все четыре стороны равны, делим 34 / 4 = 8, 5 cм. Значит ВС = 7, 5см. 2) если угол 45, то треугольник будет равнобедренный и его вторая сторона тоже будет 5 см. Из большего..

4 оси имеет прчмоугольник.

Радиус основания цилиндра S1 = πR² = 16π ; R² = 16 ; R = 4 см. Сторона осевого сечения равна диаметру основания цилиндра ; равна 8 см. Площадь осевого сечения равна S2 = 8² = 64 см². Ответ : 64 см².

S поверхности шара = 4πR = 2. 5S = 4 * π *  = 4 * π * 6. 25 = 25π.

Какая фигура имеет четыре стороны одной длинны? (квадрат) перимет какой геометрической фигуры равен — (a + b)•2.

Вот вроде, думаю правильно.

Рассмотрим треугольники rsd и psd pd = rd — дано rs = ps — дано ds — общая сторона треугольники rsd и psd равны, следовательно угол pds = углу rds угол pds + угол rds = 360 — 98 = 262 (град. ) угол rds = 262 : 2 = 131 (град. ).

Ответы и решения на фото.

H = √3a / 2 r = √3a / 6 — радиус вписанной окружности R = √3a / 3 — радиус описанной окружности.

Если mh 3 см, а угол mnh 30°, то mh по свойству прямоугольного треугольника = 1 / 2 mn, значит mn 6 см отсюда mn = pq = 6 см mq = mh + hq = 5 + 3 = 8 см mq = np = 8 см находим углы hnp = 90° по свойству перпендикуляра, значит угол n получается угол m..

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Признаки параллельности прямых

1. Первый признак параллельности.

Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти прямые параллельны.

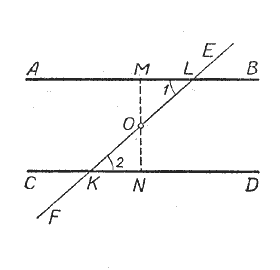
Пусть прямые АВ и СD пересечены прямой ЕF и ∠1 = ∠2. Возьмём точку О — середину отрезка КL секущей ЕF (рис.).

Опустим из точки О перпендикуляр ОМ на прямую АВ и продолжим его до пересечения с прямой СD, АВ ⊥ МN. Докажем, что и СD ⊥ МN.

Для этого рассмотрим два треугольника: МОЕ и NОК. Эти треугольники равны между собой. В самом деле: ∠1 = ∠2 по условию теоремы; ОK = ОL — по построению;

∠МОL = ∠NОК, как вертикальные углы. Таким образом, сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника; следовательно, ΔМОL = ΔNОК, а отсюда и ∠LМО = ∠КNО,
но ∠LМО прямой, значит, и ∠КNО тоже прямой. Таким образом, прямые АВ и СD перпендикулярны к одной и той же прямой МN, следовательно, они параллельны, что и требовалось доказать.

Примечание. Пересечение прямых МО и СD может быть установлено путём поворота треугольника МОL вокруг точки О на 180°.

2. Второй признак параллельности.

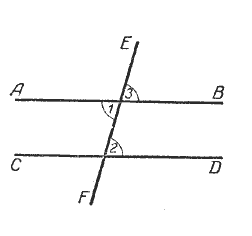
Посмотрим, будут ли параллельны прямые АВ и СD, если при пересечении их третьей прямой ЕF равны соответственные углы.

Пусть какие-нибудь соответственные углы равны, например ∠ 3 = ∠2 (рис.);

∠3 = ∠1, как углы вертикальные; значит, ∠2 будет равен ∠1. Но углы 2 и 1 — внутренние накрест лежащие углы, а мы уже знаем, что если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти прямые параллельны. Следовательно, АВ || СD.

Если при пересечении двух прямых третьей соответственные углы равны, то эти две прямые параллельны.

На этом свойстве основано построение параллельных прямых при помощи линейки и чертёжного треугольника. Выполняется это следующим образом.

Приложим треугольник к линейке так, как это показано на рис. Будем передвигать треугольник так, чтобы одна его сторона скользила по линейке, а по какой-либо другой стороне треугольника проведём несколько прямых. Эти прямые будут параллельны.

3. Третий признак параллельности.

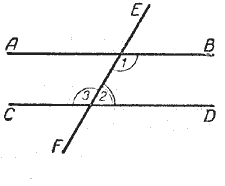
Пусть нам известно, что при пересечении двух прямых АВ и СD третьей прямой сумма каких-нибудь внутренних односторонних углов равна 2d (или 180°). Будут ли в этом случае прямые АВ и СD параллельны (рис.).

Пусть ∠1 и ∠2-внутренние односторонние углы и в сумме составляют 2d.

Но ∠3 + ∠2 = 2d, как углы смежные. Следовательно, ∠1 + ∠2 = ∠3+ ∠2.

Отсюда ∠1 = ∠3, а эти углы внутренние накрест лежащие. Следовательно, АВ || СD.

Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 2d (или 180°), то эти две прямые параллельны.

Признаки параллельных прямых:

1. Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти прямые параллельны.

2.Если при пересечении двух прямых третьей соответственные углы равны, то эти две прямые параллельны.

3. Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то эти две прямые параллельны.

4. Если две прямые параллельны третьей прямой, то они параллельны между собой.

5. Если две прямые перпендикулярны третьей прямой, то они параллельны между собой.

Видео:ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ 4. Углы, образованные при пересечении двух параллельных прямых третьейСкачать

Аксиома параллельности Евклида

Задача. Через точку М, взятую вне прямой АВ, провести прямую, параллельную прямой АВ.

Пользуясь доказанными теоремами о признаках параллельности прямых, можно эту задачу решить различными способами,

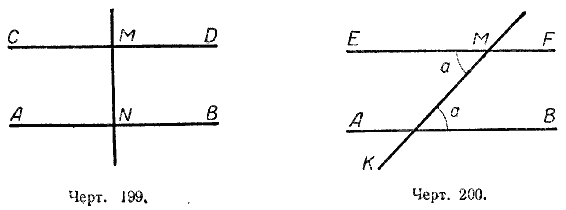
Решение. 1-й с п о с о б (черт. 199).

Проводим МN⊥АВ и через точку М проводим СD⊥МN;

получаем СD⊥МN и АВ⊥МN.

На основании теоремы («Если две прямые перпендикулярны к одной и той же прямой, то они параллельны.») заключаем, что СD || АВ.

2-й с п о с о б (черт. 200).

Проводим МК, пересекающую АВ под любым углом α, и через точку М проводим прямую ЕF, образующую с прямой МК угол ЕМК, равный углу α. На основании теоремы (Признаки параллельности прямых) заключаем, что ЕF || АВ.

Решив данную задачу, можем считать доказанным, что через любую точку М, взятую вне прямой АВ, можно провести прямую, ей параллельную. Возникает вопрос, сколько же прямых, параллельных данной прямой и проходящих через данную точку, может существовать?

Практика построений позволяет предполагать, что существует только одна такая прямая, так как при тщательно выполненном чертеже прямые, проведённые различными способами через одну и ту же точку параллельно одной и той же прямой, сливаются.

В теории ответ на поставленный вопрос даёт так называемая аксиома параллельности Евклида; она формулируется так:

Через точку, взятую вне дaнной прямой, можно провести только одну прямую, параллельную этой прямой.

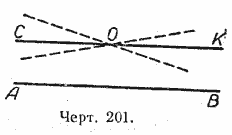
На чертеже 201 через точку О проведена прямая СК, параллельная прямой АВ.

Всякая другая прямая, проходящая через точку О, уже не будет параллельна прямой АВ, а будет её пересекать.

Принятая Евклидом в его «Началах» аксиома, которая утверждает, что на плоскости через точку, взятую вне данной прямой, можно провести только одну прямую, параллельную этой прямой, называется аксиомой параллельности Евклида.

Более двух тысячелетий после Евклида многие учёные-математики пытались доказать это математическое предложение, но всегда их попытки оказывались безуспешными. Только в 1826 г. великий русский учёный, профессор Казанского университета Николай Иванович Лобачевский доказал, что, используя все другие аксиомы Евклида, это математическое предложение доказать нельзя, что оно действительно должно быть принято за аксиому. Н. И. Лобачевский создал новую геометрию, которая в отличие от геометрии Евклида названа геометрией Лобачевского.

💡 Видео

ГЕОМЕТРИЯ 7 класс. Признаки параллельности, накрест лежащие, соответственные и односторонние углыСкачать

№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

Геометрия 7 класс Атанасян, Бутузов Вопросы к Главе 3Скачать

№208. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50°Скачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

Признаки параллельности прямых. Геометрия. 7 КлассСкачать

УГЛЫ ПРИ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ И СЕКУЩЕЙСкачать