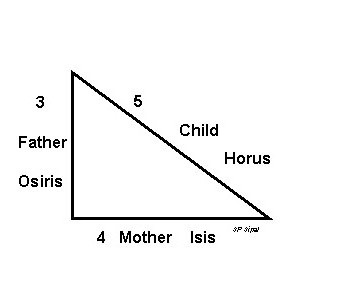
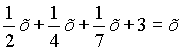Известный математик Пифагор совершил множество различных открытий, но большинству людей, которым не приходится регулярно сталкиваться с алгеброй и геометрией, он известен благодаря своей теореме. Ученый открыл ее, пребывая в Египте, где его очаровала красота и изящность пирамид, а это, в свою очередь, натолкнуло его на мысль о том, что в их формах прослеживается определенная закономерность.
- История открытия
- Применение
- Доказательство
- Египетский треугольник 6 8 10
- Задача на смекалку
- 1. Практическая работа
- 2. Устная работа
- 3. Практическая работа
- Пифагорова тройка — это упорядоченный набор из трех натуральных чисел (x, y, z), которые удовлетворяют квадратному уравнению:
- Пифагоровы числа — это числа x, y, z, которые образуют Пифагорову тройку.
- В примитивной тройке (x, y, z) числа x и y разной четности, причем, четное число должно делиться на 4, и или x или y должно делиться на 3. А число z – всегда – нечётное.
- Любая примитивная тройка представляется в виде:
- Другими словами, катеты (x, y) и гипотенузу (z) пифагорова треугольника можно выразить следующими формулами:
- Во всяком пифагоровом треугольнике хотя бы один из катетов делится на 3 и хотя бы один из катетов делится на 4 (это может быть один и тот же катет).
- Ответ
- Египетский треугольник
- Задача на смекалку
- 1. Практическая работа
- 2. Устная работа
- 3. Практическая работа
- 🌟 Видео
Видео:Египетский треугольник #огэ #математика #shortsСкачать

История открытия
Своим названием египетский треугольник обязан эллинам, которые часто посещали Египет в VII-V веках до н. э., среди них был и Пифагор. Основой пирамиды Хеопса является прямоугольный многоугольник, а
Видео:Пифагоровы тройки 1. Египетский треугольникСкачать

Применение
Египетский треугольник с древности пользовался популярностью в архитектуре и строительстве.
Соотношение сторон этого треугольника 3:4:5 приводит к тому, что он является прямоугольным, т. е. один угол равен 90 градусам, а два других – 53,13 и 36,87 градусам. Прямым является угол между сторонами, соотношение которых равно 3:4.
Видео:Египетский треугольник. Пифагоровы тройки.Скачать

Доказательство
При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3 2 х 4 2 = 5 2 , следовательно, он является прямоугольным.
Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.
Видео:Что такое египетский треугольник?Скачать

Египетский треугольник 6 8 10
Разделы: Математика
Очень важно, чтобы материал, с которым учащиеся познакомятся на уроке, вызвал у них интерес.
Уделом истины не может быть забвенье,
Как только мир ее увидит взор,
И теорема та, что дал нам Пифагор,
Верна теперь, как в день ее рожденья.
За светлый луч с небес вознес благодаренье
Мудрец богам не так, как было до тех пор.
Ведь целых сто быков послал он под топор,
Чтоб их сожгли как жертвоприношенье.
Быки с тех пор, как только весть услышат,
Что новой истины уже следы видны,
Отчаянно мычат и ужаса полны:
Им Пифагор навек внушил тревогу.
Не в силах преградить той истине дорогу,
Они, закрыв глаза, дрожат и еле дышат.
(А. фон Шамиссо, перевод Хованского)
Пифагор, VI в. до н. э. (580 – 500), древнегреческий философ и математик. Первым заложил основы математики как науки, имел свою школу (школа Пифагора). Ему приписывают и открытие так называемой теоремы Пифагора, хотя геометрическая интерпретация этой проблемы была известна и раньше.
Задача на смекалку
Поликрат (известный из баллады Шиллера тиран с острова Самос) однажды спросил на пиру у Пифагора, сколько у того учеников. “Охотно скажу тебе, о Поликрат, – отвечал Пифагор. – Половина моих учеников изучает прекрасную математику. Четверть исследует тайны вечной природы. Седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Столько учеников веду я к рождению вечной истины”. Сколько учеников было у Пифагора?
Пусть х – число учеников Пифагора.
По условию задачи составим уравнение:
ОТВЕТ: 28 учеников.
Начнем урок в школе Пифагора.
1. Практическая работа
(Несколько человек работают у доски, остальные в тетрадях).
Задание 1. Построить треугольник по трем сторонам, если стороны равны.
в) 5, 12, 13 (единицы измерения указывать не обязательно).
Задание 2. Измерить больший угол этих треугольников.
Ответы близки к 90 о .
Учитель предлагает внимательно посмотреть на построенные треугольники, найти отличия и определить, чем эти треугольники похожи друг на друга. Класс постепенно находит нужную формулировку: “Если треугольник имеет стороны a, b, c и a 2 +b 2 =c 2 , то угол, противолежащий стороне с, прямой”.
Доказательство этой теоремы – обратной к теореме Пифагора.
2. Устная работа
1) в прямоугольном треугольнике гипотенуза и катет соответственно равны 13 и 5. Найдите второй катет.
2) в прямоугольном треугольнике катеты равны 1,5 и 2. Найдите гипотенузу.
3) определите вид треугольника, стороны которого равны 6, 8, 10.
3. Практическая работа
На тонкой веревке делают метрии, делящие ее на 12 равных частей, связывают концы, а затем растягивают веревку в виде треугольника со сторонами 3, 4, 5. Тогда угол между сторонами 3 и 4 оказывается прямым.
ВЫВОД: если стороны треугольника пропорциональны числам 3, 4 и 5, то этот треугольник прямоугольный.
Учитель говорит учащимся, что этот факт использовался египтянами для построения на местности прямых углов – ведь оптических измерительных приборов тогда еще не было, а для строительства домов, дворцов и тем более гигантских пирамид надо было уметь строить прямые углы.
(Звучит музыка. Демонстрация слайдов с изображением античных дворцов, храмов, египетских пирамид).
Перед тем как перейти к следующему этапу урока, ученики вместе с учителем еще раз делают вывод, что безошибочность построения прямых углов следует из теоремы, обратной к теореме Пифагора. Проверяют еще раз эту теорему на треугольнике со сторонами 3, 4, 5: 3 2 + 4 2 = 5 2 . Далее можно сказать, что в общем виде уравнение записывается следующим образом: а 2 + b 2 = с 2 . Необходимо проверить есть ли еще корни у этого уравнения.
Учащиеся проверяют этот факт. Прямоугольными являются также треугольники со сторонами:
Далее учитель сообщает, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.
Учитель предлагает тем учащимся, которых заинтересовала данная тема, дома доказать, что катеты a, b и гипотенуза с таких треугольников выражаются формулами:
а = 2mn, b = m 2 – n 2 , c = m 2 + n 2 ,
где m и n – любые натуральные числа, такие, что m > n.
В финале урока уместно прочитать известные стихи, посвященные теореме Пифагора.
Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
(И. Дырченко)
Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми тройками (или пифагоровыми треугольниками).
Видео:Египетский треугольникСкачать

Пифагорова тройка — это упорядоченный набор из трех натуральных чисел (x, y, z), которые удовлетворяют квадратному уравнению:
Видео:Египетский треугольникСкачать

Пифагоровы числа — это числа x, y, z, которые образуют Пифагорову тройку.
Например, к пифагоровым тройкам относятся:
- треугольник с катетами 5 и 12, и гипотенузой 13. Т.е. пифагорова тройка будет (5,12,13).
- треугольник с катетами 6 и 8, и гипотенузой 10. Т.е. пифагорова тройка будет (6,8,10).
- Среди пифагоровых треугольников особо известен египетский треугольник – треугольник со сторонами 3, 4, 5.
Пифагорову тройку (пифагоров треугольник) с катетами x, y и гипотенузой z принято обозначать (x, y, z):
Примитивная Пифагорова тройка (Простейшая Пифагорова тройка) – это тройка чисел (x, y, z), которые являются взаимно простыми числами и имеют наибольший общий знаменатель, равный 1.
Если предположить, что два из чисел тройки имеют простой общий делитель p, то из уравнения тройки следует, то на p будет делится и третье число z. Это противоречит тому, что тройка — простейшая.
Из каждой примитивной тройки можно получить другую Пифагорову тройку, умножив x, y, z на одно и то же натуральное число k.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

В примитивной тройке (x, y, z) числа x и y разной четности, причем, четное число должно делиться на 4, и или x или y должно делиться на 3. А число z – всегда – нечётное.
Другими словами, один из катетов должен быть нечетным, другой четным и делиться на 4, хотя бы один из катетов должен делиться на 3, а гипотенуза всегда нечетное число.
Формула Евклида является основным инструментом построения Пифагоровых троек.
Видео:Что такое египетский треугольник ❓Скачать

Любая примитивная тройка представляется в виде:
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Другими словами, катеты (x, y) и гипотенузу (z) пифагорова треугольника можно выразить следующими формулами:
где m, n — целые числа (m>n).
Образованные при помощи формулы Евклида тройки будут примитивными тогда и только тогда, когда m и n взаимно простые и (m-n) — нечетное число.
Если и m, и n одновременно являются нечетными, то x, y и z будут четными, а тройка не будет примитивной. Однако деление x, y и z на 2 даcт примитивную тройку, если m и n взаимно просты.
Несмотря на то, что формула Евклида генерирует все примитивные тройки, она не порождает все тройки. Но если добавить дополнительный параметр k получим формулу, порождающую все Пифагоровы треугольники единственным образом:
где m, n, k — натуральные числа; m>n; (m-n) — нечетно; m и n — взаимно простые числа.
Чтобы доказать, что последние формулы образуют пифагоровы тройки, найдем значения:
x 2 + y 2 = k(m 2 +n 2 )
таким образом, мы показали, что:
Полученная формула является определением пифагоровой тройки.
Так как любую пифагорову тройку можно разделить на некоторое k, чтобы получить примитивную тройку, то любая тройка может быть образована единственным образом с использованием m и n для создания примитивной тройки, а затем она умножается на k.
Из одного пифагорового треугольника (x, y, z) можно получить бесконечное множество подобных ему треугольников, если каждую из сторон умножить на одно и тоже натуральное число k: (kx, ky, kz), где k – любое натуральное число.
Основной треугольник среди подобных пифагоровых треугольников – это наименьший треугольник, катеты которого выражены взаимно простыми числами.
- В пифагоровой тройке (x, y, z) одно из чисел x и y всегда нечетно, гипотенуза всегда нечетная.
- Египетский треугольник – это единственный пифагоров треугольник стороны которого выражены последовательными натуральными числами: (3, 4, 5).
- Тождество Месснера задает множество пифагоровых треугольников, у которых один из катетов на 1 меньше гипотенузы:
Видео:№488. Найдите: а) высоту равностороннего треугольника, если его сторона равна 6 см;Скачать

Во всяком пифагоровом треугольнике хотя бы один из катетов делится на 3 и хотя бы один из катетов делится на 4 (это может быть один и тот же катет).
Между пифагоровыми треугольниками (a,b,c) и рациональными точками дуги единичной окружности (x 2 + y 2 = 1) в первой четверти системы координат можно установить однозначное соответствие, полагая:
3 стороны треугольника 6,8,10. назвите вид этого треугольника
- Попроси больше объяснений
- Следить
- Отметить нарушение
Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Ответ
так же этот треугольник египетский) очень поможет знание этих пар (3,4,5 и 6,8,10)
Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Египетский треугольник
Разделы: Математика
Очень важно, чтобы материал, с которым учащиеся познакомятся на уроке, вызвал у них интерес.
Уделом истины не может быть забвенье,
Как только мир ее увидит взор,
И теорема та, что дал нам Пифагор,
Верна теперь, как в день ее рожденья.
За светлый луч с небес вознес благодаренье
Мудрец богам не так, как было до тех пор.
Ведь целых сто быков послал он под топор,
Чтоб их сожгли как жертвоприношенье.
Быки с тех пор, как только весть услышат,
Что новой истины уже следы видны,
Отчаянно мычат и ужаса полны:
Им Пифагор навек внушил тревогу.
Не в силах преградить той истине дорогу,
Они, закрыв глаза, дрожат и еле дышат.
(А. фон Шамиссо, перевод Хованского)
Пифагор, VI в. до н. э. (580 – 500), древнегреческий философ и математик. Первым заложил основы математики как науки, имел свою школу (школа Пифагора). Ему приписывают и открытие так называемой теоремы Пифагора, хотя геометрическая интерпретация этой проблемы была известна и раньше.
Задача на смекалку
Поликрат (известный из баллады Шиллера тиран с острова Самос) однажды спросил на пиру у Пифагора, сколько у того учеников. “Охотно скажу тебе, о Поликрат, — отвечал Пифагор. – Половина моих учеников изучает прекрасную математику. Четверть исследует тайны вечной природы. Седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Столько учеников веду я к рождению вечной истины”. Сколько учеников было у Пифагора?
Пусть х – число учеников Пифагора.
По условию задачи составим уравнение:
ОТВЕТ: 28 учеников.
Начнем урок в школе Пифагора.
1. Практическая работа
(Несколько человек работают у доски, остальные в тетрадях).
Задание 1. Построить треугольник по трем сторонам, если стороны равны.
в) 5, 12, 13 (единицы измерения указывать не обязательно).
Задание 2. Измерить больший угол этих треугольников.
Ответы близки к 90 о .
Учитель предлагает внимательно посмотреть на построенные треугольники, найти отличия и определить, чем эти треугольники похожи друг на друга. Класс постепенно находит нужную формулировку: “Если треугольник имеет стороны a, b, c и a 2 +b 2 =c 2 , то угол, противолежащий стороне с, прямой”.
Доказательство этой теоремы – обратной к теореме Пифагора.
2. Устная работа
1) в прямоугольном треугольнике гипотенуза и катет соответственно равны 13 и 5. Найдите второй катет.
2) в прямоугольном треугольнике катеты равны 1,5 и 2. Найдите гипотенузу.
3) определите вид треугольника, стороны которого равны 6, 8, 10.
3. Практическая работа
На тонкой веревке делают метрии, делящие ее на 12 равных частей, связывают концы, а затем растягивают веревку в виде треугольника со сторонами 3, 4, 5. Тогда угол между сторонами 3 и 4 оказывается прямым.
ВЫВОД: если стороны треугольника пропорциональны числам 3, 4 и 5, то этот треугольник прямоугольный.
Учитель говорит учащимся, что этот факт использовался египтянами для построения на местности прямых углов – ведь оптических измерительных приборов тогда еще не было, а для строительства домов, дворцов и тем более гигантских пирамид надо было уметь строить прямые углы.
(Звучит музыка. Демонстрация слайдов с изображением античных дворцов, храмов, египетских пирамид).
Перед тем как перейти к следующему этапу урока, ученики вместе с учителем еще раз делают вывод, что безошибочность построения прямых углов следует из теоремы, обратной к теореме Пифагора. Проверяют еще раз эту теорему на треугольнике со сторонами 3, 4, 5: 3 2 + 4 2 = 5 2 . Далее можно сказать, что в общем виде уравнение записывается следующим образом: а 2 + b 2 = с 2 . Необходимо проверить есть ли еще корни у этого уравнения.
Учащиеся проверяют этот факт. Прямоугольными являются также треугольники со сторонами:
- 5, 12, 13;
- 8, 15, 17;
- 7, 24, 25.
Далее учитель сообщает, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.
Учитель предлагает тем учащимся, которых заинтересовала данная тема, дома доказать, что катеты a, b и гипотенуза с таких треугольников выражаются формулами:
а = 2mn, b = m 2 — n 2 , c = m 2 + n 2 ,
где m и n – любые натуральные числа, такие, что m > n.
В финале урока уместно прочитать известные стихи, посвященные теореме Пифагора.
Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
(И. Дырченко)
🌟 Видео
90 задач по геометрии решается этим способом!Скачать
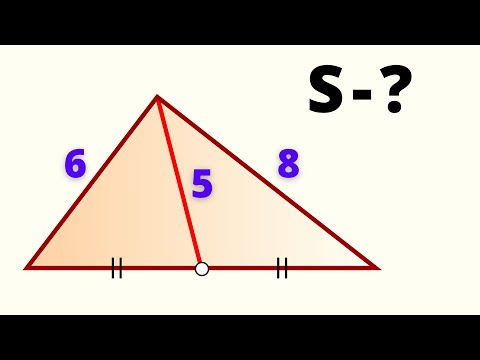
Нахождение стороны прямоугольного треугольникаСкачать

Египетский треугольник, теорема ПифагораСкачать

Египетский треугольникСкачать

Теорема Пифагора для чайников)))Скачать

Задача 6 №27619 ЕГЭ по математике. Урок 67Скачать

№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Делаем Египетский треугольник из верёвочки с узелками. Геометрия для детей. Математика - это красивоСкачать