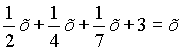Египетские треугольники 8 10

Знали ли в древнем Египте математику и геометрию? Не только знали, но и постоянно использовали ее при создании архитектурных шедевров и даже. при ежегодной разметке полей, на которых вода при наводнении уничтожала все межи. Даже существовала специальная служба землемеров, которые быстро с помощью геометрических приемов восстанавливали границы полей, когда вода спадала.

Пока неизвестно, как мы будем называть наше молодое поколение, которое вырастает на компьютерах, позволяющих не заучивать наизусть таблицу умножения и не производить в уме другие элементарные математические вычисления или геометрические построения. Может быть, человекороботами или киборгами. Греки же называли тех, кто не мог без посторонней помощи доказать простую теорему, профанами. Поэтому не удивительно, что саму теорему, которая широко использовалась в прикладных науках, в том числе и для разметки полей или строительства пирамид, древние греки называли «мостом ослов». А они очень хорошо знали египетскую математику.

Видео:Что такое египетский треугольник?Скачать

Полезно вспомнить

Треугольник

Треугольник прямолинейный, часть плоскости, ограниченная тремя отрезками прямых (стороны Треугольника (в геометрии)), имеющими попарно по одному общему концу (вершины Треугольника (в геометрии)). Треугольник, у которого длины всех сторон равны, называется равносторонним, или правильным, Треугольник с двумя равными сторонами — равнобедренным. Треугольник называется остроугольным, если все углы его острые; прямоугольным — если один из его углов прямой; тупоугольным — если один из его углов тупой. Более одного прямого или тупого угла Треугольник (в геометрии) иметь не может, так как сумма всех трёх углов равна двум прямым углам (180° или, в радианах, p). Площадь Треугольник (в геометрии) равна ah/2, где а — любая из сторон Треугольника, принимаемая за его основание, a h — соответствующая высота. Стороны Треугольника подчинены условию: длина каждой из них меньше суммы и больше разности длин двух других сторон.

Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.

• Трём точкам пространства, не лежащим на одной прямой, соответствует одна и только одна плоскость.
• Любой многоугольник можно разбить на треугольники — этот процесс называется триангуляция.
• Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.

Типы треугольников

Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:

• Если все углы треугольника острые, то треугольник называется остроугольным;
• Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
• Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.

По числу равных сторон

• Разносторонним называется треугольник, у которого длины трёх сторон попарно различны.
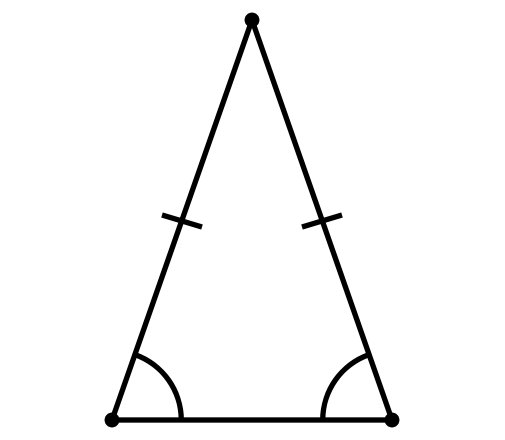
• Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
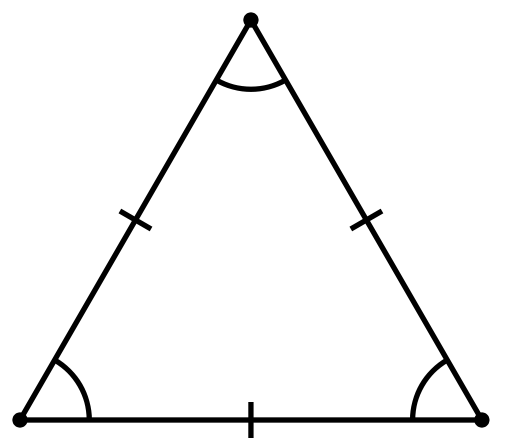
• Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.

Видео:Египетский треугольникСкачать

Египетский треугольник

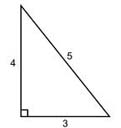
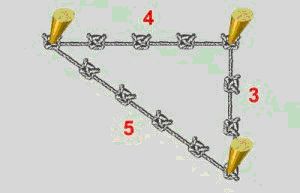
Египетский треугольник – прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности.

Итак, с чего же начать? Разве вот с этого: 3 + 5 = 8. а число 4 составляет половину числа 8. Стоп! Числа 3, 5, 8. Разве они не напоминают что-то очень знакомое? Ну конечно, они имеют прямое отношение к золотому сечению и входят в так называемый «золотой ряд»: 1, 1, 2, 3, 5, 8, 13, 21. В этом ряду каждый последующий член равен сумме двух предыдущих: 1 + 1= 2. 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8 и так далее. Выходит, что египетский треугольник имеет отношение к золотому сечению? И древние египтяне знали, с чем имели дело? Но не будем торопиться с выводами. Необходимо выяснить детали поточнее.

Выражение «золотое сечение», как считают некоторые, впервые ввел в XV веке Леонардо да Винчи. Но сам «золотой ряд» стал известен в 1202 году, когда его впервые опубликовал в своей «Книге о счете» итальянский математик Леонардо Пизанский. Прозванный Фибоначчи. Однако почти за две тысячи лет до них золотое сечение было известно Пифагору и его ученикам. Правда, называлось оно по-другому, как «деление в среднем и крайнем отношении». А вот египетский треугольник с его «золотым сечением» был известен еще в те далекие времена, когда строились пирамиды в Египте, когда процветала Атлантида.

Для доказательства теоремы о египетском треугольнике необходимо использовать отрезок прямой известной длины А-А1 (рис.). Он будет служить масштабом, единицей измерения, и позволит определить длину всех сторон треугольника. Три отрезка А-А1 равны по длине наименьшей из сторон треугольника ВС, у которой соотношение равно 3. А четыре отрезка А-А1 равны по длине второй стороне, у которой соотношение выражается числом 4. И, наконец, длина третьей стороны равна пяти отрезкам А-А1. А дальше, как говорится, дело техники. На бумаге проведем отрезок ВС, являющийся наименьшей стороной треугольника. Затем из точки В радиусом, равным отрезку с соотношением 5, проводим циркулем дугу окружности, а из точки С —дугу окружности радиусом, равным длине отрезка с соотношением 4. Если теперь точку пересечения дуг соединить линиями с точками В и С, то получим прямоугольный треугольнике соотношением сторон 3 : 4 : 5.

Что и требовалось доказать.

Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами. Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.

Видео:Египетский треугольник. Пифагоровы тройки.Скачать

Египетский треугольник — загадка древности

Каждому из вас известно, что Пифагор был великим математиком, который внес неоценимый вклад в развитие алгебры и геометрии, но еще больше он завоевал известность благодаря своей теореме.

А открыл Пифагор теорему Египетского треугольника в то время, когда ему довелось побывать в Египте. Пребывая в этой стране, ученый был очарован великолепием и красотой пирамид. Возможно, как раз это и стало толчком, который подверг его на мысль о том, что в формах пирамид четко прослеживается какая-то определенная закономерность.

Видео:Египетский треугольникСкачать

История открытия

Название египетский треугольник получил благодаря эллинам и Пифагору, которые были частыми гостями в Египте. И случилось это приблизительно в VII-V веках до н. э.

Знаменитая пирамида Хеопса, вообще-то представляет собой прямоугольный многоугольник, а вот священным египетским треугольником принято считать пирамиду Хефрена.

Жители Египта природу Египетского треугольника, как писал Плутарх, сопоставляли с семейным очагом. В их трактовках можно было услышать, что в этой геометрической фигуре ее вертикальный катет символизировал мужчину, основание фигуры относилось к женскому началу, а гипотенузе пирамиды отводилась роль ребенка.

А уже из изученной темы вам хорошо известно, что соотношение сторон этой фигуры равно 3:4:5 и, следовательно, что это нас приводит к теореме Пифагора, так как 32 + 42= 52.

И если учесть, что в основании пирамиды Хефрена лежит египетский треугольник, то можно сделать вывод, народ древнего мира знал знаменитую теорему еще задолго до того, как она была сформулирована Пифагором.

Основной особенностью египетского треугольника, скорее всего, было его своеобразное соотношение сторон, которое было первым и простейшим из Героновых треугольников, так как и стороны, и его площадь имели целые числа.

Видео:Египетский треугольник #огэ #математика #shortsСкачать

Особенности египетского треугольника

А теперь давайте более подробно остановимся на отличительных особенностях египетского треугольника:

• Во-первых, как мы уже говорили, все его стороны и площадь состоят из целых чисел;

• Во-вторых, по теореме Пифагора нам известно, что сумма квадратов катетов равна квадрату гипотенузе;

• В-третьих, с помощью такого треугольника можно отмерять прямые углы в пространстве, что очень удобно и необходимо при строительстве сооружений. А удобство заключается в том, что мы знаем, что этот треугольник является прямоугольным.

• В-четвертых, как нам тоже уже известно, что даже если нет соответствующих измерительных приборов, то этот треугольник можно запросто построить с помощью простой веревки.

Видео:Геометрия 8. Урок 10 - Теорема Пифагора. Наклонная и проекция.Скачать

Применение египетского треугольника

В Древние века в архитектуре и строительстве египетский треугольник пользовался огромной популярностью. Особенно он был необходим, если для построения прямого угла использовали веревку или шнур.

Ведь известно, что отложить прямой угол в пространстве, является довольно таки сложным занятием и поэтому предприимчивые египтяне изобрели интересный способ построения прямого угла. Для этих целей они брали веревку, на которой отмечали узелками двенадцать ровных частей и потом с этой веревки складывали треугольник, со сторонами, которые равнялись 3 , 4 и 5 частям и в итоге без проблем, получали прямоугольный треугольник. Благодаря такому замысловатому инструменту, египтяне с огромной точностью размеряли землю для сельскохозяйственных работ, строили дома и пирамиды.

Вот так посещение Египта и изучение особенностей египетской пирамиды подтолкнуло Пифагора на открытие своей теоремы, которая, кстати, попала в Книгу Рекордов Гиннеса, как теорема, которая имеет самое большое количество доказательств.

Видео:Пифагоровы тройки 1. Египетский треугольникСкачать

Интересный факт

Треугольные колеса Рело

Колесо — круглый (как правило), свободно вращающийся или закреплённый на оси диск, позволяющий поставленному на него телу катиться, а не скользить. Колесо повсеместно используется в различных механизмах и инструментах. Широко применяется для транспортировки грузов.

Колесо существенно уменьшает затраты энергии на перемещение груза по относительно ровной поверхности. При использовании колеса работа совершается против силы трения качения, которая в искусственных условиях дорог существенно меньше, чем сила трения скольжения. Колёса бывают сплошные (например, колёсная пара железнодорожного вагона) и состоящие из довольно большого количества деталей, к примеру, в состав автомобильного колеса входит диск, обод, покрышка, иногда камера, болты крепления и тд. Износ покрышек автомобилей является почти решённой проблемой (при правильно установленных углах колёс). Современные покрышки проезжают свыше 100 000 км. Нерешённой проблемой является износ покрышек у колёс самолётов. При соприкосновении неподвижного колеса с бетонным покрытием взлётной полосы на скорости в несколько сотен километров в час износ покрышек огромен.

• В июле 2001 года на колесо был получен инновационный патент со следующей формулировкой: «круглое устройство, применяемое для транспортировки грузов». Этот патент был выдан Джону Кэо, юристу из Мельбурна, который хотел тем самым показать несовершенство австралийского патентного закона.
• Французская компания Мишлен в 2009 году разработала пригодное к массовому выпуску автомобильное колесо Active Wheel со встроенными электродвигателями, приводящими в действие колесо, рессору, амортизатор и тормоз. Таким образом, эти колёса делают ненужными следующие системы автомобиля: двигатель, сцепление, коробку передач, дифференциал, приводной и карданный валы.
• В 1959 году американец А. Сфредд получил патент на квадратное колесо. Оно легко шло по снегу, песку, грязи, преодолевало ямы. Вопреки опасениям, машина на таких колёсах не «хромала» и развивала скорость до 60 км/ч.

Франц Рело (Franz Reuleaux, 30 сентября 1829 — 20 августа 1905) — немецкий инженер-механик, лектор Берлинской Королевской Технической академии, ставший впоследствии ее президентом. Первым, в 1875 году, разработал и изложил основные положения структуры и кинематики механизмов; занимался проблемами эстетичности технических объектов, промышленным дизайном, в своих конструкциях придавал большое значение внешним формам машин. Рело часто называют отцом кинематики.

Видео:Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Египетский треугольник 8 10

Видео:Что такое египетский треугольник ❓Скачать

Планиметрия. Страница 5

Видео:ЕГЭ 2024. ВСЁ ПРО ТРЕУГОЛЬНИКИ за 15 минутСкачать

1.Теорема Пифагора

Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Доказательство.

1. Разделим каждую сторону большого квадрата на два отрезка x и y точкой. И проведем через эти точки отрезки.

2. Тогда треугольники 1,2,3,4 равны по двум сторонам и углу между ними.

3. Т.к. сумма углов α + β = 90°, то фигура внутри большого квадрата тоже квадрат. (Все стороны = с и все углы = 90° )

4. Площадь большого квадрата равна сумме площадей малого квадрата и 4-х треугольников. (Рис.1)

Рис.1 Теорема Пифагора.

Видео:Египетский треугольникСкачать

2.Египетский треугольник

Пусть дан треугольник со сторонами АВ = a, ВС = b, АС = c. При условии, что а 2 + b 2 = с 2 . Доказать, что угол, лежащий против стороны с, прямой.

Допустим, что треугольник АВС не прямоугольный. Тогда можно опустить высоту на сторону АС — h (Рис.2). Из двух прямоугольных треугольников ABD и DBC составим следующую систему уравнений по теореме Пифагора. Обозначим AD как х, BD — высота h.

Но по условию задачи а 2 + b 2 = с 2 . Следовательно х = 0 и сторона а = h. Т.е. угол между сторонами АВ и АС — прямой.

В древнем Египте данное соотношение применялось очень широко. Например для построения прямого угла между сторонами при строительстве зданий и сооружений. Или при измерении прямых углов пахотных земель. Так как зная соотношение, можно легко построить прямой угол. По этой причине треугольник со сторонами 3,4,5 ед. называют Египетским треугольником.

Рис.2 Египетский треугольник.

Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

3.Соотношение между углами и сторонами в прямоугольном треугольнике

Пусть дан прямоугольный треугольник АВС. Проведем прямую ЕF параллельную стороне АВ (Рис.3). Тогда по теореме о пропорциональных отрезках:

Т.е. соs α не зависит от размеров прямоугольного треугольника, а зависит только от величины угла. Тогда по теореме Пифагора sin α также зависит только от величины угла. А следовательно tg α и ctg α.

Отсюда можно сделать следующие выводы:

AB = BC sin α
AC = BC cos α
AB = AC tg α
AC = AB ctg α

Рис.3 Соотношение между углами и сторонами в прямоугольном треугольнике.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

4.Основные тригонометрические тождества

Пусть дан прямоугольный треугольник со сторонами a,b,c. (Рис.4)

Рис.4 Основные тригонометрические тождества.

5.Пример 1

У треугольника одна сторона равна 1 м, а прилегающие к ней углы 30° и 45°. Найдите другие стороны треугольника. (рис.5)

Так как один из углов 30 градусов, то катет, лежащий против этого угла равен половине гипотенузы, т.е. h = b/2. А следовательно КС = h, т.к. угол β = 45 градусов.

Рис.5 Задача. У треугольника одна сторона равна 1 м.

Пример 2

Найдите высоту равнобокой трапеции, если ее основания равны 6 м и 12 м, а боковая сторона равна 5 м. (Рис.6)

Решение:

Пусть ABCD данная трапеция. ВЕ перпендикуляр, опущенный на основание AD. Тогда АЕ = (12 — 6)/ 2 = 3 м. Так как АЕ = FD.

По теореме Пифагора:

АВ 2 = AE 2 + BE 2

Рис.6 Задача. Найдите высоту равнобокой трапеции.

Пример 3

Докажите, что расстояние между двумя точками на сторонах треугольника не больше большей из его сторон. (Рис.7)

Доказательство:

Пусть ABC данный треугольник. АС — его большая сторона. Проведем отрезок DE параллельно стороне АС. Необходимо доказать, что отрезок DE меньше стороны АС. Если мы докажем, что отрезок DE меньше большей стороны АС, то при взятии двух других точек треугольника на других его меньших сторонах, отрезок между этими точками будет также меньше стороны АС.

Опустим перпендикуляр BF на большую сторону АС. Составим следующее соотношение:

АС = АВ сos α + ВС cos β

Тогда отрезок DE будет равен:

DE = DB сos α + ВE cos β

Так как DB Рис.7 Задача. Докажите, что расстояние между двумя точками.

Пример 4

Докажите, что прямая, отстоящая от центра окружности на расстояние меньше радиуса, пересекает окружность в двух точках. (Рис.8)

Доказательство:

Пусть дана окружность с центром в точке О. И прямая а, отстоящая от центра окружности точки О, на расстояние ОЕ = h h, то прямая а будет иметь две точки пересечения. Так как

h = ОА*cos α = ОВ*cos (-α)

Радиусы ОА и ОВ можно рассматривать как две наклонные, отложенные в двух полуплоскостях, в треугольнике АОВ перпендикуляра ОЕ.

Рис.8 Задача. Докажите, что прямая, отстоящая от центра окружности.

Пример 5

Даны три положительных числа a,b,c. Докажите, что если каждое из этих чисел меньше суммы двух других, то существует треугольник со сторонами a,b,c. (Рис.9)

Доказательство:

Пусть даны три точки. Если эти три точки лежат на одной прямой, например А,Е,С, то расстояния между этими точками связаны соотношением: АС = АЕ + ЕС

Отсюда видно, что каждое из трех расстояний не больше двух других. Т.е. расстояние между точками А и С не больше двух расстояний АЕ и ЕС.

Если взять три точки, не лежащих на одной прямой, например А,В,С и опустить перпендикуляр ВЕ, то АС AB + BC (Рис.9 б). Тогда концы отрезков АВ и СВ не смогут совпасть в точке В. Так как, если даже отрезки такой же длины отложить на отрезке АС, то получится, что

Таким образом, если числа a,b и с принять за длины отрезков, то концы отрезков АВ и СВ не смогут совпасть в одной точке В. Между ними образуется некое расстояние ВВ₁ и построить треугольник не получится.

Рис.9 Задача. Даны три положительных числа.

Видео:Плавпрактика. Путешествие вокруг света: Эпизод 8 из 8 - Атлантика, Канада, дембель. #моряки #флотСкачать

Египетский треугольник 6 8 10

Разделы: Математика

Очень важно, чтобы материал, с которым учащиеся познакомятся на уроке, вызвал у них интерес.

Уделом истины не может быть забвенье,
Как только мир ее увидит взор,
И теорема та, что дал нам Пифагор,
Верна теперь, как в день ее рожденья.
За светлый луч с небес вознес благодаренье
Мудрец богам не так, как было до тех пор.
Ведь целых сто быков послал он под топор,
Чтоб их сожгли как жертвоприношенье.

Быки с тех пор, как только весть услышат,
Что новой истины уже следы видны,
Отчаянно мычат и ужаса полны:
Им Пифагор навек внушил тревогу.
Не в силах преградить той истине дорогу,
Они, закрыв глаза, дрожат и еле дышат.
(А. фон Шамиссо, перевод Хованского)

Пифагор, VI в. до н. э. (580 – 500), древнегреческий философ и математик. Первым заложил основы математики как науки, имел свою школу (школа Пифагора). Ему приписывают и открытие так называемой теоремы Пифагора, хотя геометрическая интерпретация этой проблемы была известна и раньше.

Задача на смекалку

Поликрат (известный из баллады Шиллера тиран с острова Самос) однажды спросил на пиру у Пифагора, сколько у того учеников. “Охотно скажу тебе, о Поликрат, – отвечал Пифагор. – Половина моих учеников изучает прекрасную математику. Четверть исследует тайны вечной природы. Седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Столько учеников веду я к рождению вечной истины”. Сколько учеников было у Пифагора?

Пусть х – число учеников Пифагора.

По условию задачи составим уравнение:

ОТВЕТ: 28 учеников.

Начнем урок в школе Пифагора.

1. Практическая работа

(Несколько человек работают у доски, остальные в тетрадях).

Задание 1. Построить треугольник по трем сторонам, если стороны равны.

в) 5, 12, 13 (единицы измерения указывать не обязательно).

Задание 2. Измерить больший угол этих треугольников.

Ответы близки к 90 о .

Учитель предлагает внимательно посмотреть на построенные треугольники, найти отличия и определить, чем эти треугольники похожи друг на друга. Класс постепенно находит нужную формулировку: “Если треугольник имеет стороны a, b, c и a 2 +b 2 =c 2 , то угол, противолежащий стороне с, прямой”.

Доказательство этой теоремы – обратной к теореме Пифагора.

2. Устная работа

1) в прямоугольном треугольнике гипотенуза и катет соответственно равны 13 и 5. Найдите второй катет.

2) в прямоугольном треугольнике катеты равны 1,5 и 2. Найдите гипотенузу.

3) определите вид треугольника, стороны которого равны 6, 8, 10.

3. Практическая работа

На тонкой веревке делают метрии, делящие ее на 12 равных частей, связывают концы, а затем растягивают веревку в виде треугольника со сторонами 3, 4, 5. Тогда угол между сторонами 3 и 4 оказывается прямым.

ВЫВОД: если стороны треугольника пропорциональны числам 3, 4 и 5, то этот треугольник прямоугольный.

Учитель говорит учащимся, что этот факт использовался египтянами для построения на местности прямых углов – ведь оптических измерительных приборов тогда еще не было, а для строительства домов, дворцов и тем более гигантских пирамид надо было уметь строить прямые углы.

(Звучит музыка. Демонстрация слайдов с изображением античных дворцов, храмов, египетских пирамид).

Перед тем как перейти к следующему этапу урока, ученики вместе с учителем еще раз делают вывод, что безошибочность построения прямых углов следует из теоремы, обратной к теореме Пифагора. Проверяют еще раз эту теорему на треугольнике со сторонами 3, 4, 5: 3 2 + 4 2 = 5 2 . Далее можно сказать, что в общем виде уравнение записывается следующим образом: а 2 + b 2 = с 2 . Необходимо проверить есть ли еще корни у этого уравнения.

Учащиеся проверяют этот факт. Прямоугольными являются также треугольники со сторонами:

Далее учитель сообщает, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.

Учитель предлагает тем учащимся, которых заинтересовала данная тема, дома доказать, что катеты a, b и гипотенуза с таких треугольников выражаются формулами:

а = 2mn, b = m 2 – n 2 , c = m 2 + n 2 ,

где m и n – любые натуральные числа, такие, что m > n.

В финале урока уместно прочитать известные стихи, посвященные теореме Пифагора.

Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
(И. Дырченко)

Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми тройками (или пифагоровыми треугольниками).

Видео:Делаем Египетский треугольник из верёвочки с узелками. Геометрия для детей. Математика - это красивоСкачать

Пифагорова тройка — это упорядоченный набор из трех натуральных чисел (x, y, z), которые удовлетворяют квадратному уравнению:

Видео:Египетский треугольникСкачать

Пифагоровы числа — это числа x, y, z, которые образуют Пифагорову тройку.

Например, к пифагоровым тройкам относятся:

• треугольник с катетами 5 и 12, и гипотенузой 13. Т.е. пифагорова тройка будет (5,12,13).
• треугольник с катетами 6 и 8, и гипотенузой 10. Т.е. пифагорова тройка будет (6,8,10).
• Среди пифагоровых треугольников особо известен египетский треугольник – треугольник со сторонами 3, 4, 5.

Пифагорову тройку (пифагоров треугольник) с катетами x, y и гипотенузой z принято обозначать (x, y, z):

Примитивная Пифагорова тройка (Простейшая Пифагорова тройка) – это тройка чисел (x, y, z), которые являются взаимно простыми числами и имеют наибольший общий знаменатель, равный 1.

Если предположить, что два из чисел тройки имеют простой общий делитель p, то из уравнения тройки следует, то на p будет делится и третье число z. Это противоречит тому, что тройка — простейшая.

Из каждой примитивной тройки можно получить другую Пифагорову тройку, умножив x, y, z на одно и то же натуральное число k.

Видео:Египетский треугольник, теорема ПифагораСкачать

В примитивной тройке (x, y, z) числа x и y разной четности, причем, четное число должно делиться на 4, и или x или y должно делиться на 3. А число z – всегда – нечётное.

Другими словами, один из катетов должен быть нечетным, другой четным и делиться на 4, хотя бы один из катетов должен делиться на 3, а гипотенуза всегда нечетное число.

Формула Евклида является основным инструментом построения Пифагоровых троек.

Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Любая примитивная тройка представляется в виде:

Видео:Решали пол-урока, а оказалось очень простоСкачать

Другими словами, катеты (x, y) и гипотенузу (z) пифагорова треугольника можно выразить следующими формулами:

где m, n — целые числа (m>n).

Образованные при помощи формулы Евклида тройки будут примитивными тогда и только тогда, когда m и n взаимно простые и (m-n) — нечетное число.

Если и m, и n одновременно являются нечетными, то x, y и z будут четными, а тройка не будет примитивной. Однако деление x, y и z на 2 даcт примитивную тройку, если m и n взаимно просты.

Несмотря на то, что формула Евклида генерирует все примитивные тройки, она не порождает все тройки. Но если добавить дополнительный параметр k получим формулу, порождающую все Пифагоровы треугольники единственным образом:

где m, n, k — натуральные числа; m>n; (m-n) — нечетно; m и n — взаимно простые числа.

Чтобы доказать, что последние формулы образуют пифагоровы тройки, найдем значения:

x 2 + y 2 = k(m 2 +n 2 )

таким образом, мы показали, что:

Полученная формула является определением пифагоровой тройки.

Так как любую пифагорову тройку можно разделить на некоторое k, чтобы получить примитивную тройку, то любая тройка может быть образована единственным образом с использованием m и n для создания примитивной тройки, а затем она умножается на k.

Из одного пифагорового треугольника (x, y, z) можно получить бесконечное множество подобных ему треугольников, если каждую из сторон умножить на одно и тоже натуральное число k: (kx, ky, kz), где k – любое натуральное число.

Основной треугольник среди подобных пифагоровых треугольников – это наименьший треугольник, катеты которого выражены взаимно простыми числами.

• В пифагоровой тройке (x, y, z) одно из чисел x и y всегда нечетно, гипотенуза всегда нечетная.
• Египетский треугольник – это единственный пифагоров треугольник стороны которого выражены последовательными натуральными числами: (3, 4, 5).
• Тождество Месснера задает множество пифагоровых треугольников, у которых один из катетов на 1 меньше гипотенузы:

Видео:Египетский треугольник, свойстваСкачать

Во всяком пифагоровом треугольнике хотя бы один из катетов делится на 3 и хотя бы один из катетов делится на 4 (это может быть один и тот же катет).

Между пифагоровыми треугольниками (a,b,c) и рациональными точками дуги единичной окружности (x 2 + y 2 = 1) в первой четверти системы координат можно установить однозначное соответствие, полагая:

3 стороны треугольника 6,8,10. назвите вид этого треугольника

• Попроси больше объяснений
• Следить
• Отметить нарушение

Ответ

так же этот треугольник египетский) очень поможет знание этих пар (3,4,5 и 6,8,10)

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d57af4d98ba1622 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Египетский треугольник 6 8 10

Разделы: Математика

Очень важно, чтобы материал, с которым учащиеся познакомятся на уроке, вызвал у них интерес.

Уделом истины не может быть забвенье,
Как только мир ее увидит взор,
И теорема та, что дал нам Пифагор,
Верна теперь, как в день ее рожденья.
За светлый луч с небес вознес благодаренье
Мудрец богам не так, как было до тех пор.
Ведь целых сто быков послал он под топор,
Чтоб их сожгли как жертвоприношенье.

Быки с тех пор, как только весть услышат,
Что новой истины уже следы видны,
Отчаянно мычат и ужаса полны:
Им Пифагор навек внушил тревогу.
Не в силах преградить той истине дорогу,
Они, закрыв глаза, дрожат и еле дышат.
(А. фон Шамиссо, перевод Хованского)

Пифагор, VI в. до н. э. (580 – 500), древнегреческий философ и математик. Первым заложил основы математики как науки, имел свою школу (школа Пифагора). Ему приписывают и открытие так называемой теоремы Пифагора, хотя геометрическая интерпретация этой проблемы была известна и раньше.

Задача на смекалку

Поликрат (известный из баллады Шиллера тиран с острова Самос) однажды спросил на пиру у Пифагора, сколько у того учеников. “Охотно скажу тебе, о Поликрат, – отвечал Пифагор. – Половина моих учеников изучает прекрасную математику. Четверть исследует тайны вечной природы. Седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Столько учеников веду я к рождению вечной истины”. Сколько учеников было у Пифагора?

Пусть х – число учеников Пифагора.

По условию задачи составим уравнение:

ОТВЕТ: 28 учеников.

Начнем урок в школе Пифагора.

1. Практическая работа

(Несколько человек работают у доски, остальные в тетрадях).

Задание 1. Построить треугольник по трем сторонам, если стороны равны.

в) 5, 12, 13 (единицы измерения указывать не обязательно).

Задание 2. Измерить больший угол этих треугольников.

Ответы близки к 90 о .

Учитель предлагает внимательно посмотреть на построенные треугольники, найти отличия и определить, чем эти треугольники похожи друг на друга. Класс постепенно находит нужную формулировку: “Если треугольник имеет стороны a, b, c и a 2 +b 2 =c 2 , то угол, противолежащий стороне с, прямой”.

Доказательство этой теоремы – обратной к теореме Пифагора.

2. Устная работа

1) в прямоугольном треугольнике гипотенуза и катет соответственно равны 13 и 5. Найдите второй катет.

2) в прямоугольном треугольнике катеты равны 1,5 и 2. Найдите гипотенузу.

3) определите вид треугольника, стороны которого равны 6, 8, 10.

3. Практическая работа

На тонкой веревке делают метрии, делящие ее на 12 равных частей, связывают концы, а затем растягивают веревку в виде треугольника со сторонами 3, 4, 5. Тогда угол между сторонами 3 и 4 оказывается прямым.

ВЫВОД: если стороны треугольника пропорциональны числам 3, 4 и 5, то этот треугольник прямоугольный.

Учитель говорит учащимся, что этот факт использовался египтянами для построения на местности прямых углов – ведь оптических измерительных приборов тогда еще не было, а для строительства домов, дворцов и тем более гигантских пирамид надо было уметь строить прямые углы.

(Звучит музыка. Демонстрация слайдов с изображением античных дворцов, храмов, египетских пирамид).

Перед тем как перейти к следующему этапу урока, ученики вместе с учителем еще раз делают вывод, что безошибочность построения прямых углов следует из теоремы, обратной к теореме Пифагора. Проверяют еще раз эту теорему на треугольнике со сторонами 3, 4, 5: 3 2 + 4 2 = 5 2 . Далее можно сказать, что в общем виде уравнение записывается следующим образом: а 2 + b 2 = с 2 . Необходимо проверить есть ли еще корни у этого уравнения.

Учащиеся проверяют этот факт. Прямоугольными являются также треугольники со сторонами:

Далее учитель сообщает, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.

Учитель предлагает тем учащимся, которых заинтересовала данная тема, дома доказать, что катеты a, b и гипотенуза с таких треугольников выражаются формулами:

а = 2mn, b = m 2 – n 2 , c = m 2 + n 2 ,

где m и n – любые натуральные числа, такие, что m > n.

В финале урока уместно прочитать известные стихи, посвященные теореме Пифагора.

Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
(И. Дырченко)

Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми тройками (или пифагоровыми треугольниками).

Пифагорова тройка — это упорядоченный набор из трех натуральных чисел (x, y, z), которые удовлетворяют квадратному уравнению:

Пифагоровы числа — это числа x, y, z, которые образуют Пифагорову тройку.

Например, к пифагоровым тройкам относятся:

• треугольник с катетами 5 и 12, и гипотенузой 13. Т.е. пифагорова тройка будет (5,12,13).
• треугольник с катетами 6 и 8, и гипотенузой 10. Т.е. пифагорова тройка будет (6,8,10).
• Среди пифагоровых треугольников особо известен египетский треугольник – треугольник со сторонами 3, 4, 5.

Пифагорову тройку (пифагоров треугольник) с катетами x, y и гипотенузой z принято обозначать (x, y, z):

Примитивная Пифагорова тройка (Простейшая Пифагорова тройка) – это тройка чисел (x, y, z), которые являются взаимно простыми числами и имеют наибольший общий знаменатель, равный 1.

Если предположить, что два из чисел тройки имеют простой общий делитель p, то из уравнения тройки следует, то на p будет делится и третье число z. Это противоречит тому, что тройка — простейшая.

Из каждой примитивной тройки можно получить другую Пифагорову тройку, умножив x, y, z на одно и то же натуральное число k.

В примитивной тройке (x, y, z) числа x и y разной четности, причем, четное число должно делиться на 4, и или x или y должно делиться на 3. А число z – всегда – нечётное.

Другими словами, один из катетов должен быть нечетным, другой четным и делиться на 4, хотя бы один из катетов должен делиться на 3, а гипотенуза всегда нечетное число.

Формула Евклида является основным инструментом построения Пифагоровых троек.

Любая примитивная тройка представляется в виде:

Другими словами, катеты (x, y) и гипотенузу (z) пифагорова треугольника можно выразить следующими формулами:

где m, n — целые числа (m>n).

Образованные при помощи формулы Евклида тройки будут примитивными тогда и только тогда, когда m и n взаимно простые и (m-n) — нечетное число.

Если и m, и n одновременно являются нечетными, то x, y и z будут четными, а тройка не будет примитивной. Однако деление x, y и z на 2 даcт примитивную тройку, если m и n взаимно просты.

Несмотря на то, что формула Евклида генерирует все примитивные тройки, она не порождает все тройки. Но если добавить дополнительный параметр k получим формулу, порождающую все Пифагоровы треугольники единственным образом:

где m, n, k — натуральные числа; m>n; (m-n) — нечетно; m и n — взаимно простые числа.

Чтобы доказать, что последние формулы образуют пифагоровы тройки, найдем значения:

x 2 + y 2 = k(m 2 +n 2 )

таким образом, мы показали, что:

Полученная формула является определением пифагоровой тройки.

Так как любую пифагорову тройку можно разделить на некоторое k, чтобы получить примитивную тройку, то любая тройка может быть образована единственным образом с использованием m и n для создания примитивной тройки, а затем она умножается на k.

Из одного пифагорового треугольника (x, y, z) можно получить бесконечное множество подобных ему треугольников, если каждую из сторон умножить на одно и тоже натуральное число k: (kx, ky, kz), где k – любое натуральное число.

Основной треугольник среди подобных пифагоровых треугольников – это наименьший треугольник, катеты которого выражены взаимно простыми числами.

• В пифагоровой тройке (x, y, z) одно из чисел x и y всегда нечетно, гипотенуза всегда нечетная.
• Египетский треугольник – это единственный пифагоров треугольник стороны которого выражены последовательными натуральными числами: (3, 4, 5).
• Тождество Месснера задает множество пифагоровых треугольников, у которых один из катетов на 1 меньше гипотенузы:

Во всяком пифагоровом треугольнике хотя бы один из катетов делится на 3 и хотя бы один из катетов делится на 4 (это может быть один и тот же катет).

Между пифагоровыми треугольниками (a,b,c) и рациональными точками дуги единичной окружности (x 2 + y 2 = 1) в первой четверти системы координат можно установить однозначное соответствие, полагая:

3 стороны треугольника 6,8,10. назвите вид этого треугольника

• Попроси больше объяснений
• Следить
• Отметить нарушение

Ответ

так же этот треугольник египетский) очень поможет знание этих пар (3,4,5 и 6,8,10)