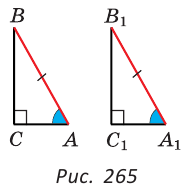
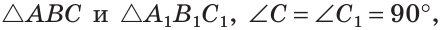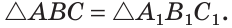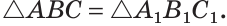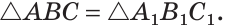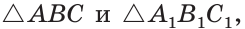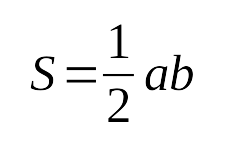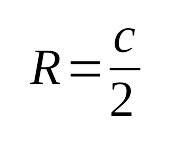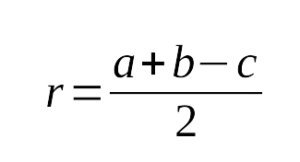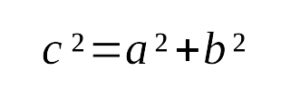Содержание:
Признаки равенства прямоугольных треугольников:
Вы уже знаете три признака равенства треугольников. Поскольку часто приходится иметь дело с прямоугольными треугольниками, то выделяют пять признаков равенства прямоугольных треугольников. Сформулируем и докажем их.
- Второй признак (по катету и прилежащему острому углу)
- Третий признак (по катету и противолежащему острому углу)
- Четвертый признак (по гипотенузе и острому углу)
- Пятый признак (по катету и гипотенузе).
- Прямоугольный треугольник: Признаки Равенства и Подобия
- Определение
- Свойства прямоугольного треугольника
- Признаки равенства прямоугольных треугольников
- Признаки прямоугольного треугольника
- Признаки подобия прямоугольных треугольников
- Признаки равенства прямоугольных треугольников
- 35 Comments
- 🎦 Видео
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать
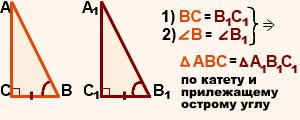
Второй признак (по катету и прилежащему острому углу)
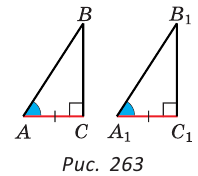
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано: 
Доказать: 
Доказательство:
по стороне и двум прилежащим к ней углам.
Видео:Признаки равенства треугольников. 7 класс.Скачать
Третий признак (по катету и противолежащему острому углу)
Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано: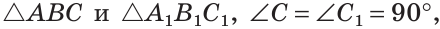 
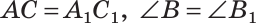
(рис. 264).
Доказать: 
Доказательство:
Сумма острых углов прямоугольного треугольника равна 90°. Из того, что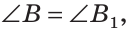 
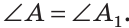
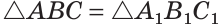
следует, что 
Тогда 
по стороне и двум прилежащим к ней углам.
Видео:7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать
Четвертый признак (по гипотенузе и острому углу)
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано: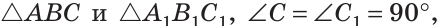 
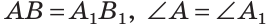
(рис. 265).
Доказать: 
Доказательство:
Сумма острых углов прямоугольного треугольника равна 90°. Из того, что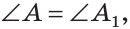 
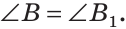
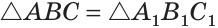
следует, что 
Тогда 
по стороне и двум прилежащим к ней углам.
Видео:Геометрия 7. Урок 9 - Признаки равенства прямоугольных треугольниковСкачать
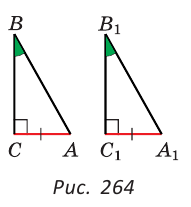
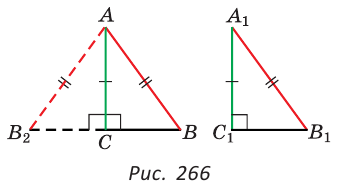
Пятый признак (по катету и гипотенузе).
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Дано: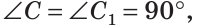 
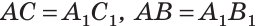
(рис. 266).
Доказать: 
Доказательство:
Приложим треугольников А1В1С1 к треугольнику АВС так, чтобы совместились равные катеты А1С1 и АС, а вершины В1 и В лежали по разные стороны от прямой АС. Треугольник А1В1С1 займет положение треугольника АВ2С. Так как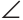 
B2CB — развернутый и АВ2 = АВ, то треугольник В2АВ — равнобедренный, катет АС — его высота. По свойству равнобедренного треугольника высота, проведенная к основанию, будет и медианой. Тогда В2С=СВ и треугольники ABC и АВ2С равны по двум катетам.
Отсюда
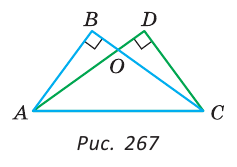
Пример:
На рисунке 267 
Доказать равенство треугольников: а) 
АВС и 
ADC б) 
АОВ и 
COD.
Доказательство:
а) Рассмотрим прямоугольные треугольники ABC и ADC. У них гипотенуза АС — общая, катеты AD и ВС равны по условию. Тогда АВС =ADC по катету и гипотенузе.
б) Из равенства треугольников ABC и ADC следует равенство сторон АВ и CD (доказано в пункте а). Тогда АОВ =COD. по катету (АВ = CD) и противолежащему острому углу (
AOB =
COD как вертикальные).
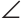
Пример:
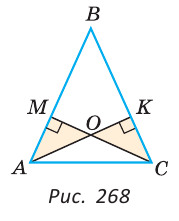
Дан треугольник ABC, АК и СМ — его высоты, проведенные к боковым сторонам, О — точка их пересечения (рис. 268). Доказать, что если треугольники АОМ и СОК равны, то треугольник ABC — равнобедренный.
Доказательство:
Так как 
AOM =
COK как вертикальные, то 
MAO =
KCO (сумма острых углов прямоугольного треугольника 90°). Из равенства треугольников АОМ и СОК следует равенство гипотенуз АО и СО. Треугольник АОС — равнобедренный,
OAC =
OCA как углы при основании равнобедренного треугольника. Тогда 
BAC =
BCA как составленные из равных углов. Треугольник ABC равнобедренный по признаку равнобедренного треугольника. Что и требовалось доказать.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Задачи на построение по геометрии
- Угол — определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать
Прямоугольный треугольник: Признаки Равенства и Подобия
Видео:Первый признак равенства треугольников. 7 класс.Скачать
Определение
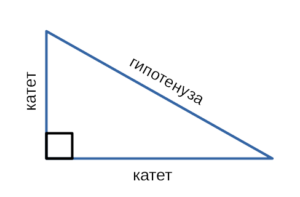
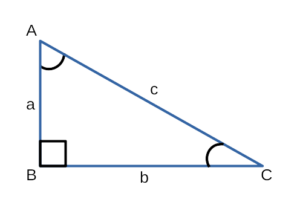
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.
Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.
Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.
Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать
Свойства прямоугольного треугольника
В прямоугольном треугольнике:
- Сумма острых углов 90˚.
- Катет, противолежащий углу в 30˚, равен половине гипотенузы.
- Медиана, проведенная к гипотенузе, равна ее половине.
- Центр описанной окружности — середина гипотенузы.
Формулы:
- Площадь прямоугольного треугольника равна
половине произведения катетов: - Радиус описанной окружности около прямоугольного
треугольника равен половине гипотенузы: - Радиус вписанной окружности в прямоугольный треугольник
выражается следующим образом: - Квадрат гипотенузы равен сумме квадратов катетов:
Видео:Признаки равенства треугольников. Практическая часть. 7 класс.Скачать
Признаки равенства прямоугольных треугольников
С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.
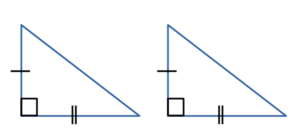
- По двум катетам:
Если два катета одного прямоугольного треугольника соответственно
равны двум катетам другого прямоугольного треугольника,
то такие треугольники равны. - По катету и гипотенузе:
Если катет и гипотенуза одного прямоугольного треугольника соответственно
равны катету и гипотенузе другого прямоугольного треугольника,
то такие треугольники равны. - По гипотенузе и острому углу:
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно
равны гипотенузе и острому углу другого прямоугольного треугольника,
то такие треугольникиравны. - По катету и острому углу:
Если катет и острый угол одного прямоугольного треугольника соответственно
равны катету и острому углу другого прямоугольного треугольника,
то такие треугольники равны.
Видео:7 класс, 20 урок, Третий признак равенства треугольниковСкачать
Признаки прямоугольного треугольника
С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.
- По теореме Пифагора:
Если квадрат стороны равен сумме квадратов двух других сторон,
то треугольник прямоугольный. - По центру описанной окружности:
Если центр описанной окружности лежит на стороне треугольника,
то треугольник прямоугольный. - По медиане:
Если медиана треугольника равна половине стороны, к которой она проведена,
то треугольник прямоугольный. - По площади:
Если площадь треугольника равна половине произведения двух его сторон,
то треугольник прямоугольный. - По радиусу описанной окружности:
Если радиус описанной окружности равен половине,
то треугольник прямоугольный.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Признаки подобия прямоугольных треугольников
С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.
Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать
Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников позволяют доказать равенство треугольников всего по двум парам элементов.
Признак равенства прямоугольных треугольников по двум катетам
Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
Признак равенства прямоугольных треугольников по катету и гипотенузе
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Признак равенства по гипотенузе и острому углу
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Признак равенства прямоугольных треугольников по катету и острому углу
1) Признак равенства прямоугольных треугольников по катету и прилежащему острому углу
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
2) Признак равенства прямоугольных треугольников по катету и противолежащему острому углу
Если катет и противолежащий ему острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему ему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать
35 Comments
Спасибо, все коротко и ясно.
спасибо большое) доступно все объяснили
А где пятый признак?
Max, признак равенства прямоугольных треугольников по катету и острому углу разбивается на два признака: по катету и противолежащему углу и по катету и прилежащему углу, потому что доказывают их отдельно.
Можно написать 5-ый признак равенства прямоугольных треугольников исходя из третьего признака равенства треугольников(не обязательно прямоугольных): если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны.
Спасибо выручили.
Очень рад, что всё так доступно и понятно.
есть еще по катету и противолежащему острому углу
Да, признак равенства по катету и острому углу иногда разбивают на два.
Офигенно! Большое спасибо!
Спс,как раз геометрию не слушал.
В геометрии знание теории — основа. Поэтому желательно слушать)
все нормально конечно ,но было бы лучше если б было доно.
Это разве не нужно доказывать ? Плз ответ, у меня экзамен будет и нужно знать,надо это доказывать или прочитать хватит ?
Роман, если использовать признаки равенства в ходе решения других задач, то каждый раз доказывать их не нужно.
Спасибо у нас злая алгебраических которая ничего не объясняет поэтому никто не понял.
А вы на уроке попробуйте не шуметь. От этого выиграет и класс, и учитель.
Спасибо, помогли подготовиться к зачёту!
Удачно Вам сдать зачёт!
Скоро зачёт,и решил почитать не из учебника,а тут.Итог: Всё быстро и понятно,без так сказать «воды»,вообщем,спасибо
Игорь, удачи Вам на зачёте!
Спасибо большое у меня через 1 месяц экзамен
Илья, желаю Вам успешно сдать экзамен!
Здравствуйте. Хотелось бы к Вам обратиться по имени, но не вижу его. Спасибо Вам за сайт. Доступно, понятно, наглядно! Приятно, что при доказательстве теорем Вы стремитесь к оптимальному, более короткому пути, например в свойстве медиан треугольника. Что же касается признака равенства прямоугольных треугольников по катету и острому углу. Вы объясняли в переписке некоторым людям, что он разбивается на два признака. Тем не менее, Вы оставляете некорректную формулировку: «Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны». При этом поясняющий рисунок соответствует верному случаю и не показывает другой — неверный. Все же нужно согласиться с тем, что это два различных признака с различными формулировками, как у Вас и написано, правда в другом месте, в разделе доказательства.
С уважением,
Олег.
Здравствуйте, Олег!
Спасибо Вам за внимание к моему ресурсу.
Зовут меня Светлана Михайловна. Учу детей математике 28 лет: 16 — в школе, 12 — как репетитор. Сайты (у меня их несколько) создавала для помощи школьникам и их родителям. К сожалению, информация в учебнике не всегда изложена доступно. Очень хочется, чтобы ученики поняли, что математика (в частности, геометрия) — интересный и не такой уж сложный предмет.
Насколько я Вас поняла, Вы предлагаете разделить признаки равенства прямоугольных треугольников по катету и острому углу на два отдельных признака, как это сделано, к примеру, в учебнике Бутузова? Вы считаете, это принципиально важно для дальнейшей работы? Ведь оба признака доказаны.
Спасибо Светлана за такой отличный сайт скоро экзамен помогает надеюсь,что ваш сайт будет продвигаться вперёд,для школьников и родителей! Ещё раз спасибо!?
Никита, желаю Вам успешно сдать экзамен!
Cпасибо Вам огромное, Светлана Михайловна! Полгода геометрии прослушал, сейчас всё понятно. И всё-таки, Олег прав, по катету и острому углу — 2 различные теоремы. Скиньте ссылку на остальные Ваши сайты мне на почту, пожалуйста
С уважением,
Влад
Спасибо) помогло при подготовке к экзаменам.
Здравствуйте, Светлана Михайловна. Давно к Вам не заходил. Я оставил комментарий от 28.04.2018, касающийся теоремы:
Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Вы ответили:
«Насколько я Вас поняла, Вы предлагаете разделить признаки равенства прямоугольных треугольников по катету и острому углу на два отдельных признака…? Вы считаете, это принципиально важно для дальнейшей работы? Ведь оба признака доказаны.»
Да, это важно, поскольку Ваша формулировка неверна. Неверно, что если катет и острый прилежащий угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
С уважением
Олег Леонидович Шлейфман.
Воу, последний комментарий аж 2019 года. Спасибо всё коротко и ясно, как говорится, краткость — сестра таланта!)
🎦 Видео
Третий признак равенства треугольников | Теорема + доказательствоСкачать
7 класс, 19 урок, Второй признак равенства треугольниковСкачать
Второй признак равенства треугольников. 7 класс.Скачать
Задачи. Второй признак равенства треугольников. По рисункам. Доказать.Скачать
Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать
Третий признак равенства треугольников (доказательство) - геометрия 7 классСкачать
Первый признак равенства треугольников | Теорема + доказательствоСкачать
Задачи на доказательство равенства треугольников. Первый признак. Простые.Скачать
